Density Functional Theory for Electrons in Materials Richard

Density Functional Theory for Electrons in Materials Richard M. Martin Bands in Ga. As Prediction of Phase Diagram of Carbon at High P, T Comp. Mat. Science School 2001 Lecture 2 1

• Pseudopotentials Outline – Ab Initio -- Empirical • Bloch theorem and bands in crystals – Definition of the crystal structure and Brillouin zone in programs used in the lab (Friday) • Plane wave calculations • Iterative methods: – Krylov subspaces – Solution by energy minimization: Conjugate gradient methods – Solution by residual minimization (connnection to. VASP code that will be used by Tuttle) • Car-Parrinello ``ab initio’’ simulations • Examples Comp. Mat. Science School 2001 Lecture 2 2

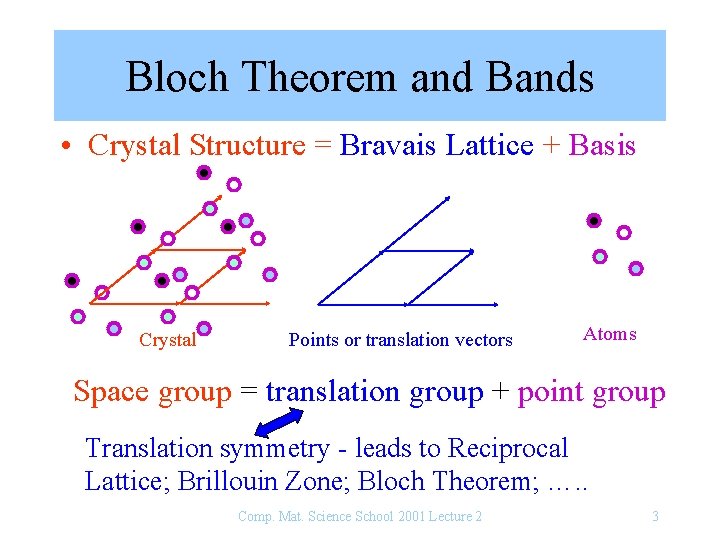
Bloch Theorem and Bands • Crystal Structure = Bravais Lattice + Basis Crystal Points or translation vectors Atoms Space group = translation group + point group Translation symmetry - leads to Reciprocal Lattice; Brillouin Zone; Bloch Theorem; …. . Comp. Mat. Science School 2001 Lecture 2 3

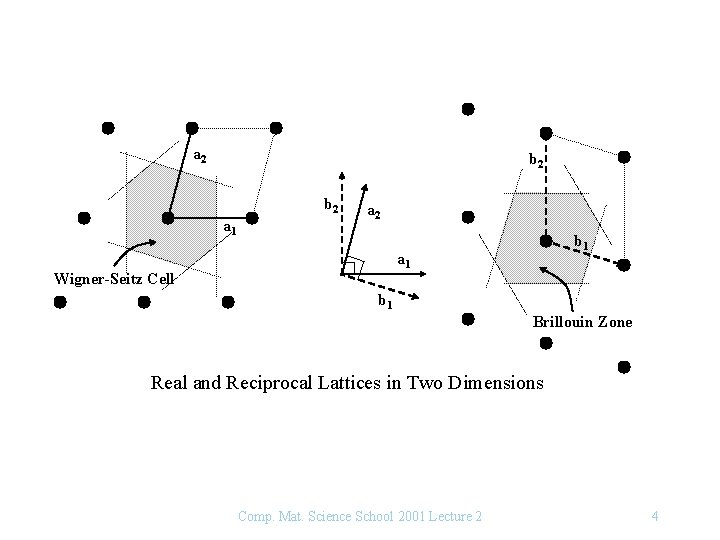
a 2 b 2 a 1 a 2 b 1 a 1 Wigner-Seitz Cell b 1 Brillouin Zone Real and Reciprocal Lattices in Two Dimensions Comp. Mat. Science School 2001 Lecture 2 4

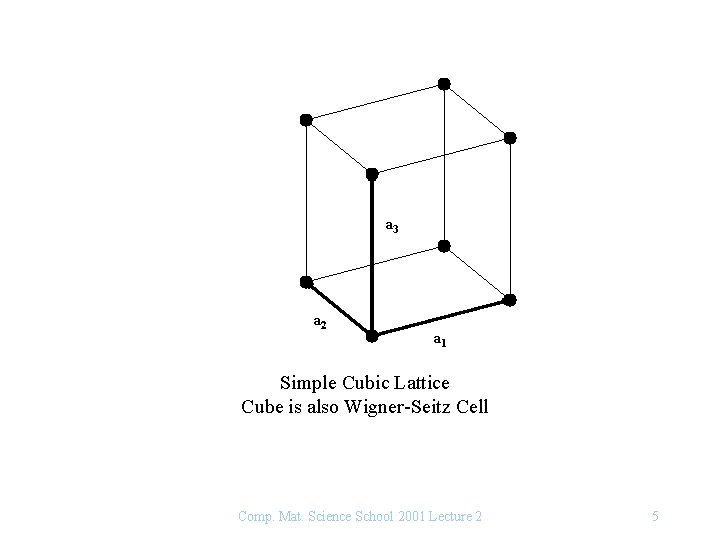
a 3 a 2 a 1 Simple Cubic Lattice Cube is also Wigner-Seitz Cell Comp. Mat. Science School 2001 Lecture 2 5

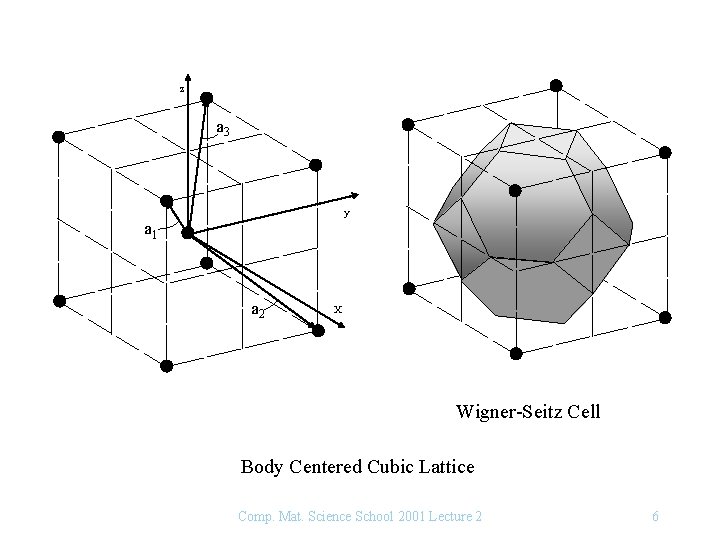
z a 3 y a 1 a 2 X Wigner-Seitz Cell Body Centered Cubic Lattice Comp. Mat. Science School 2001 Lecture 2 6

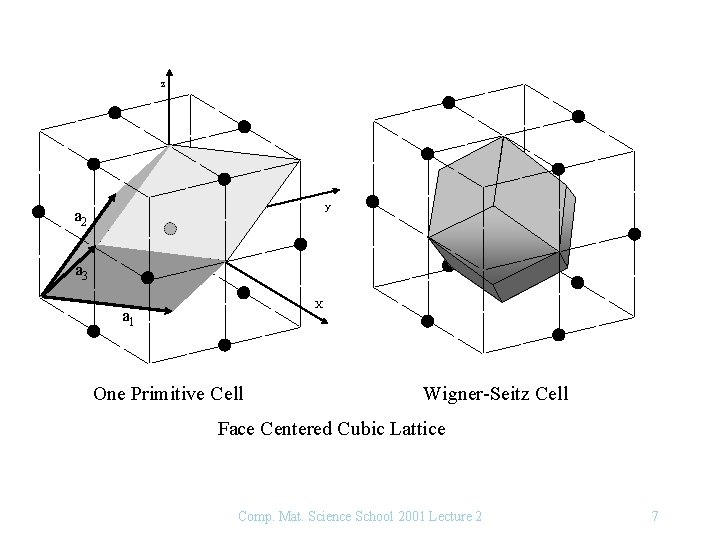
z y a 2 a 3 X a 1 One Primitive Cell Wigner-Seitz Cell Face Centered Cubic Lattice Comp. Mat. Science School 2001 Lecture 2 7

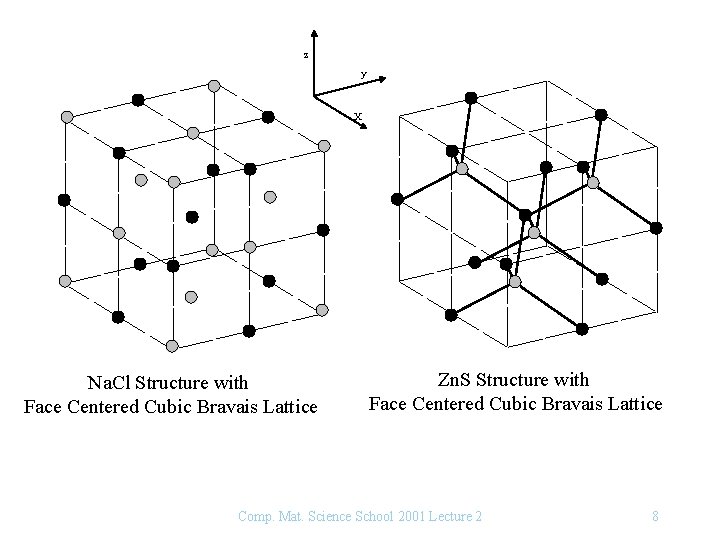
z y X Na. Cl Structure with Face Centered Cubic Bravais Lattice Zn. S Structure with Face Centered Cubic Bravais Lattice Comp. Mat. Science School 2001 Lecture 2 8

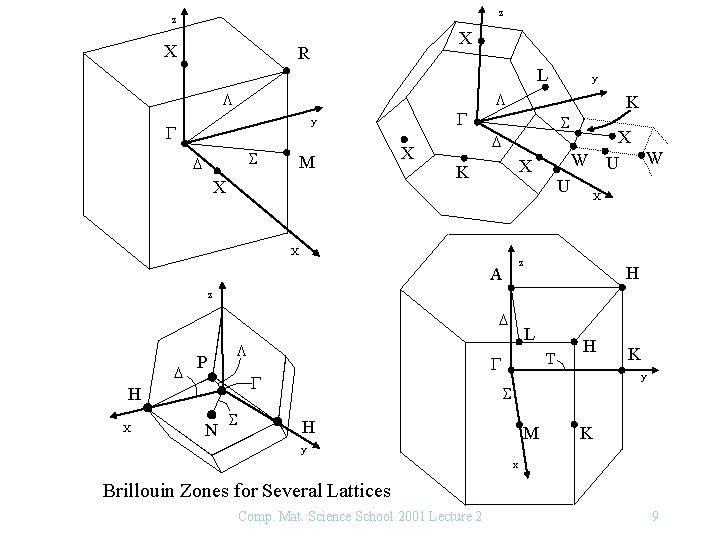
z z X X R L L G y G S D M X X y L K S D W X K U X X W U X z A H z D D P L X N S T G G H L H K y S H M K y x Brillouin Zones for Several Lattices Comp. Mat. Science School 2001 Lecture 2 9

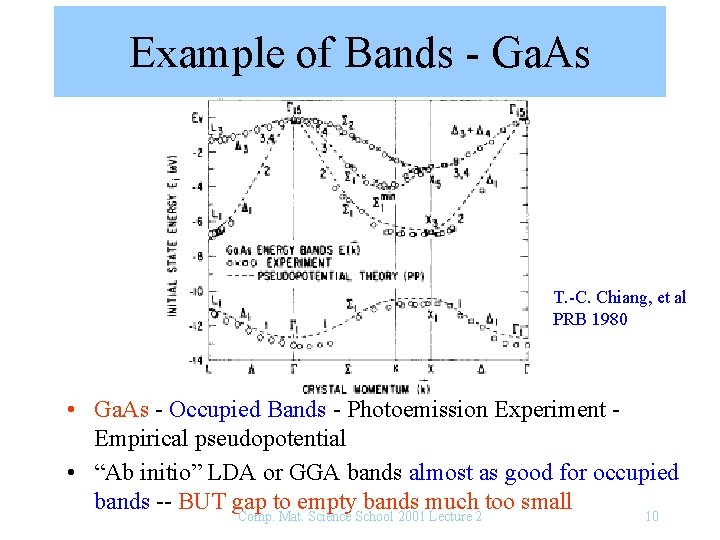
Example of Bands - Ga. As T. -C. Chiang, et al PRB 1980 • Ga. As - Occupied Bands - Photoemission Experiment Empirical pseudopotential • “Ab initio” LDA or GGA bands almost as good for occupied bands -- BUT gap to empty bands much too small Comp. Mat. Science School 2001 Lecture 2 10

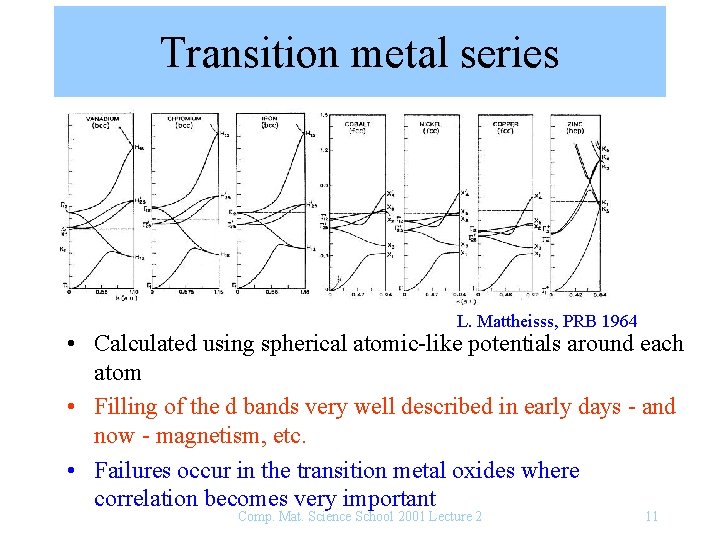
Transition metal series L. Mattheisss, PRB 1964 • Calculated using spherical atomic-like potentials around each atom • Filling of the d bands very well described in early days - and now - magnetism, etc. • Failures occur in the transition metal oxides where correlation becomes very important Comp. Mat. Science School 2001 Lecture 2 11

Standard method - Diagonalization • Kohn- Sham self Consistent Loop • Innner loop: solving equation for wavefunctions with a given Veff • Outer loop: iterating density to selfconsistency – Non-linear equations – Can be linearized near solution – Numerical methods - DIIS, Broyden, etc. (D. Johnson) See later - iterative methods Comp. Mat. Science School 2001 Lecture 2 12

Empirical pseudopotentials • Illustrate the computational intensive part of the problem – Innner loop: solving equation for wavefunctions with a given Veff – Greatly simplified program by avoiding the self -consistency • Useful for many problems • Description in technical notes and lab notes Comp. Mat. Science School 2001 Lecture 2 13

Iterative methods • Have made possible an entire new generation of simulations • Innner loop: This is where the main computation occurs – Many ideas - all with both numerical and a physical basis – Energy minimization - Conjugate gradients – Residual minimization - Davidson, DIIS, . . . – See lectures of E. de Sturler Comp. Mat. Science School 2001 Lecture 2 Used in Lab 14

Car-Parrinello Simulations • Elegant solution where the optimization of the electron wavefunctions and the ion motion are all combined in one unified algorithm Comp. Mat. Science School 2001 Lecture 2 15

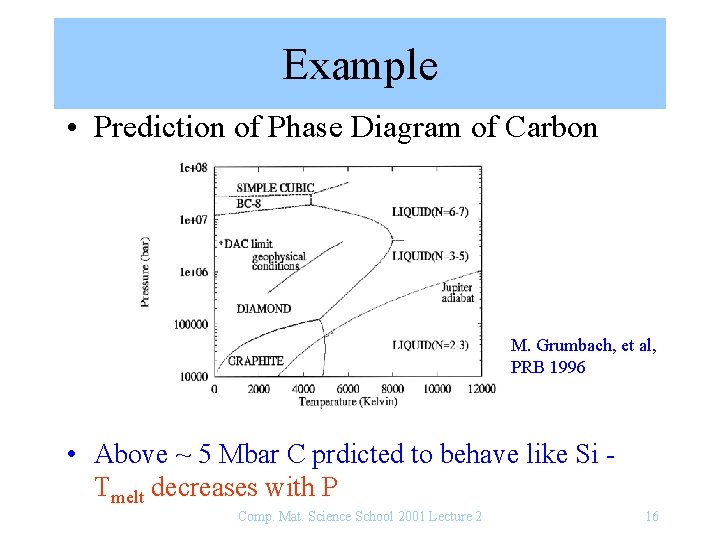
Example • Prediction of Phase Diagram of Carbon M. Grumbach, et al, PRB 1996 • Above ~ 5 Mbar C prdicted to behave like Si Tmelt decreases with P Comp. Mat. Science School 2001 Lecture 2 16

Conclusions • The ground state properties are predicted with remarkable success by the simple LDA and GGAs. – Accuracy for simple cases gives assuarnce in complex cases • Iterative methods make possible simulations far beyond anything done before – Car-Parrinello “ab initio” simulations • Greatest problem at present: Excitations – The “Band Gap Problem” Comp. Mat. Science School 2001 Lecture 2 17