Density functional theory DFT and the concepts of

Density functional theory (DFT) and the concepts of the augmented-plane-wave plus local orbitals (APW+lo) method Karlheinz Schwarz Institute of Materials Chemistry TU Wien

Walter Kohn and DFT

DFT Density Functional Theory Hohenberg-Kohn theorem The total energy of an interacting inhomogeneous electron gas in the presence of an external potential Vext(r ) is a functional of the density In DFT the many body problem of interacting electrons and nuclei is mapped to a one-electron reference system that leads to the same density as the real system. DFT treats both, exchange and correlation effects, but approximately

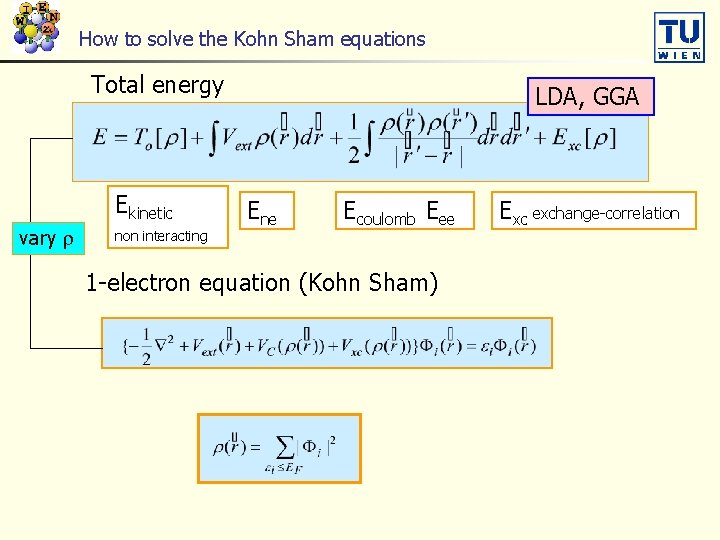
Kohn Sham equations Total energy Ekinetic vary non interacting LDA, GGA Ene Ecoulomb Eee 1 -electron equation (Kohn Sham) Exc exchange-correlation

Walter Kohn, Nobel Prize 1998 Chemistry

A simple picture of LDA Look at the “LDA” from a different angle Exc = -∫ dx n(x) e 2/ R(x) Slater, Gunnarsson-Lundqvist ………… R(x) interpreted as the radius of the ‘exchangecorrelation hole’ surrounding an electron at the point x. R(x) is a length: What length could it be? Plausible assumption, the average distance between the electrons? R(x) ≈ γ-1 n-1/3(x) Exc = - γ e 2 ∫ dx n 4/3(x)

Role of „Gradient corrected functionals“ Becke, Perdew, Wang, Lee, Yang, Parr …… ’ 87 – ‘ 92 Perdew , Burke, Ernzerhof PBE …… ‘ 96 Use n and ∂n/∂x to correct LDA in regions of low density Substantial improvement in energy differences

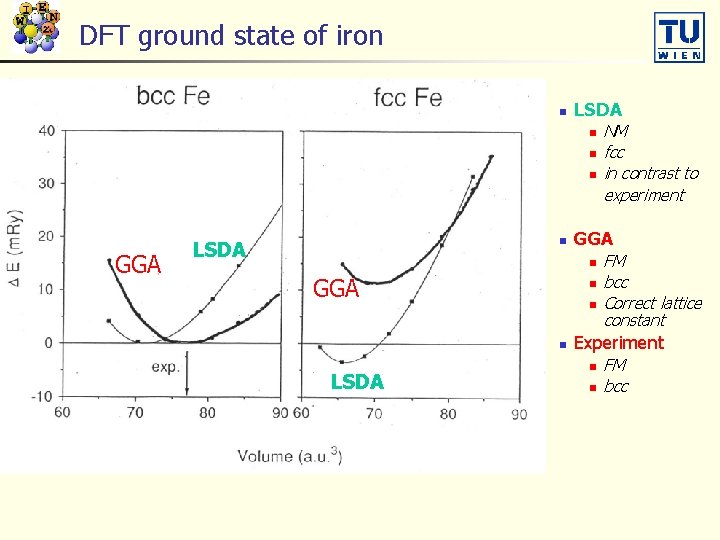
DFT ground state of iron n LSDA n n n GGA n LSDA GGA n n n LSDA NM fcc in contrast to experiment FM bcc Correct lattice constant Experiment n n FM bcc

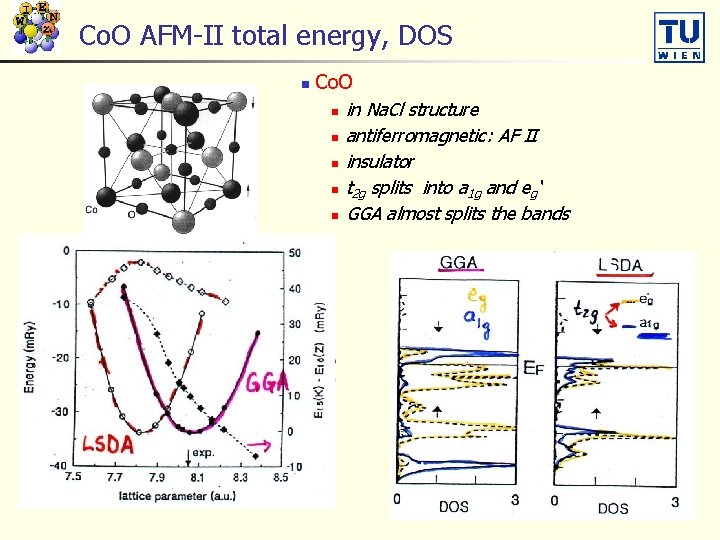
Co. O AFM-II total energy, DOS n Co. O n in Na. Cl structure n antiferromagnetic: AF II n insulator n t 2 g splits into a 1 g and eg‘ n GGA almost splits the bands

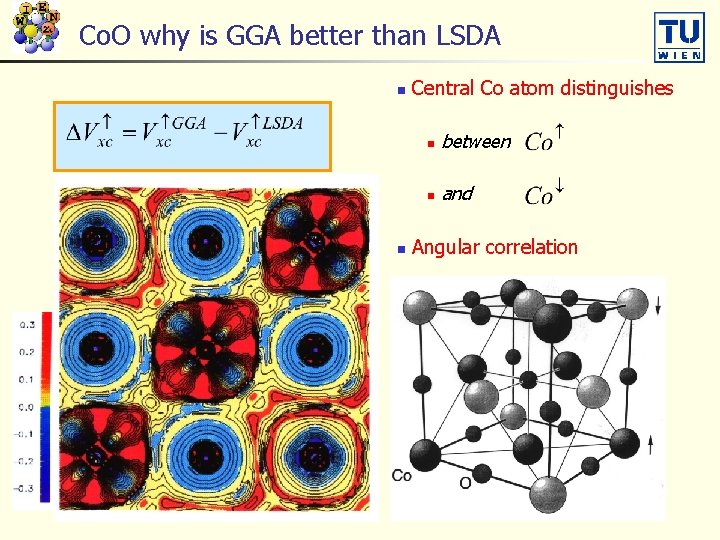
Co. O why is GGA better than LSDA n n Central Co atom distinguishes n between n and Angular correlation

DFT thanks to Claudia Ambrosch (Graz) GGA follows LDA

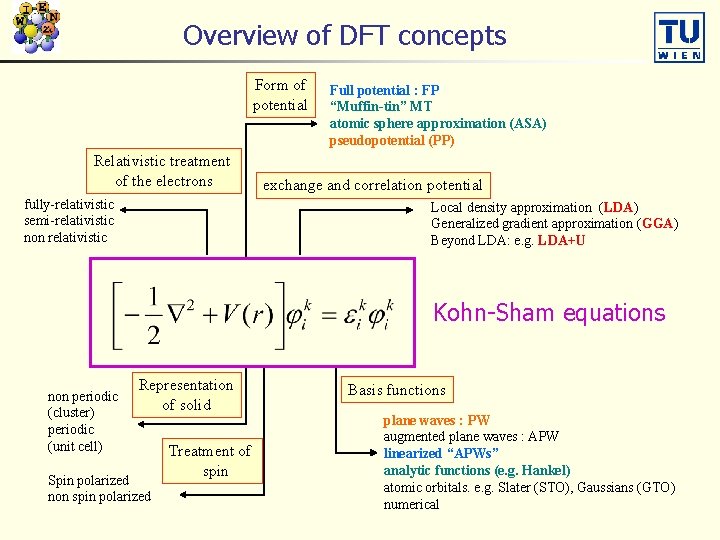
Overview of DFT concepts Form of potential Relativistic treatment of the electrons fully-relativistic semi-relativistic non relativistic Full potential : FP “Muffin-tin” MT atomic sphere approximation (ASA) pseudopotential (PP) exchange and correlation potential Local density approximation (LDA) Generalized gradient approximation (GGA) Beyond LDA: e. g. LDA+U Kohn-Sham equations non periodic (cluster) periodic (unit cell) Representation of solid Spin polarized non spin polarized Treatment of spin Basis functions plane waves : PW augmented plane waves : APW linearized “APWs” analytic functions (e. g. Hankel) atomic orbitals. e. g. Slater (STO), Gaussians (GTO) numerical

How to solve the Kohn Sham equations Total energy Ekinetic vary non interacting LDA, GGA Ene Ecoulomb Eee 1 -electron equation (Kohn Sham) Exc exchange-correlation

APW based schemes n APW (J. C. Slater 1937) Non-linear eigenvalue problem n Computationally very demanding n n LAPW (O. K. Anderssen 1975) Generalized eigenvalue problem n Full-potential n n Local orbitals (D. J. Singh 1991) n n treatment of semi-core states (avoids ghostbands) APW+lo (E. Sjöstedt, L. Nordstörm, D. J. Singh 2000) Efficiency of APW + convenience of LAPW n Basis for n K. Schwarz, P. Blaha, G. K. H. Madsen, Comp. Phys. Commun. 147, 71 -76 (2002)

APW Augmented Plane Wave method The unit cell is partitioned into: atomic spheres Interstitial region Bloch wave function: atomic partial waves Plane Waves (PWs) unit cell Rmt Full potential PW: join Atomic partial wave

Slater‘s APW (1937) Atomic partial waves Energy dependent basis functions lead to H Hamiltonian S overlap matrix Non-linear eigenvalue problem Computationally very demanding One had to numerically search for the energy, for which the det(H-ES) vanishes.

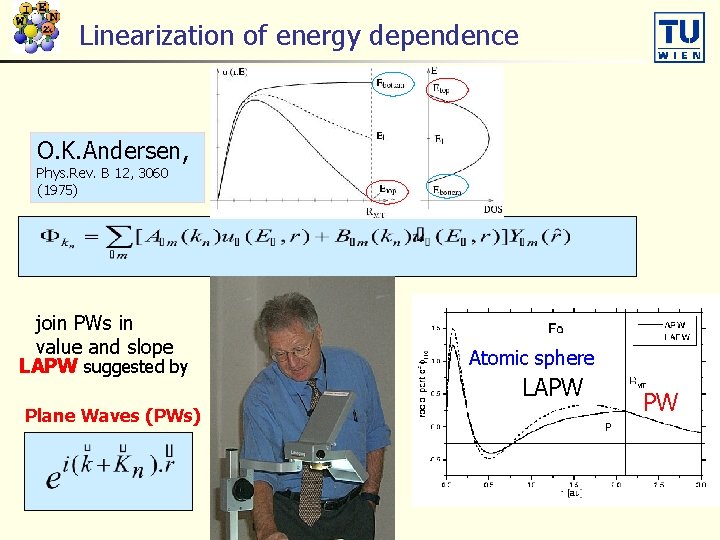
Linearization of energy dependence O. K. Andersen, Phys. Rev. B 12, 3060 (1975) join PWs in value and slope LAPW suggested by Plane Waves (PWs) Atomic sphere LAPW PW

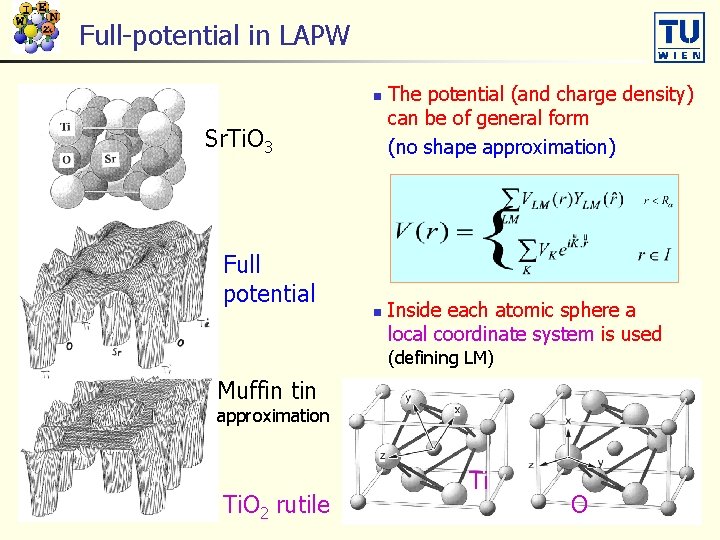
Full-potential in LAPW n Sr. Ti. O 3 Full potential n The potential (and charge density) can be of general form (no shape approximation) Inside each atomic sphere a local coordinate system is used (defining LM) Muffin tin approximation Ti. O 2 rutile Ti O

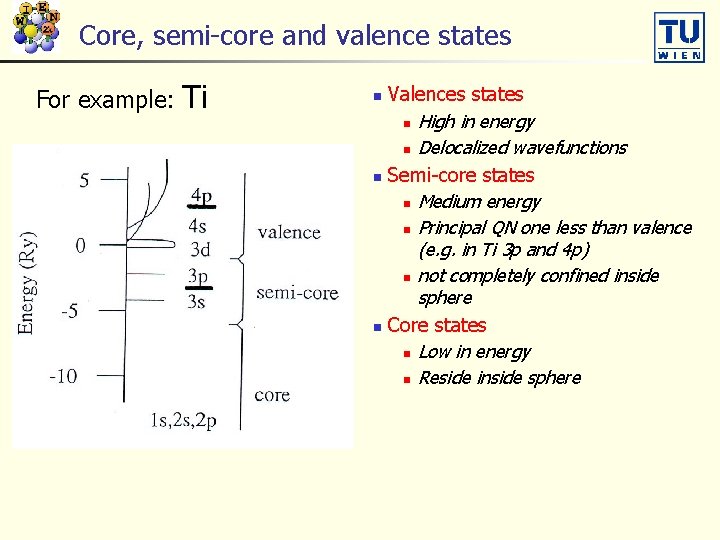
Core, semi-core and valence states For example: Ti Valences states n High in energy n Delocalized wavefunctions n Semi-core states n Medium energy n Principal QN one less than valence (e. g. in Ti 3 p and 4 p) n not completely confined inside sphere n Core states n Low in energy n Reside inside sphere n

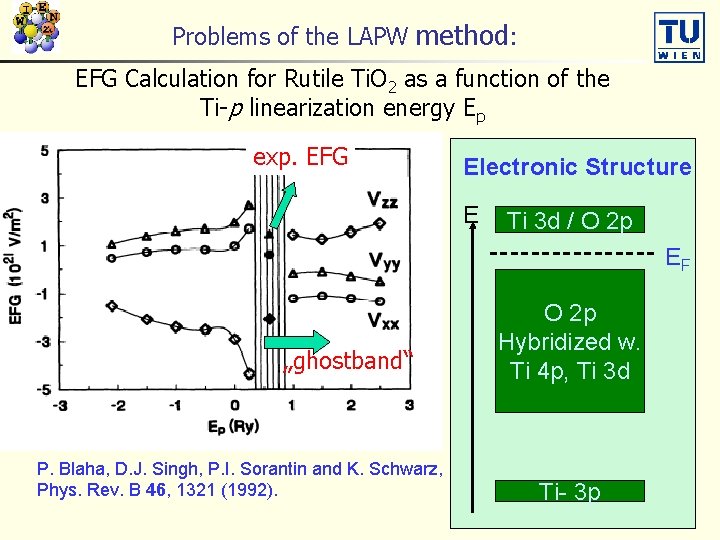
Problems of the LAPW method: EFG Calculation for Rutile Ti. O 2 as a function of the Ti-p linearization energy Ep exp. EFG Electronic Structure E Ti 3 d / O 2 p EF „ghostband“ P. Blaha, D. J. Singh, P. I. Sorantin and K. Schwarz, Phys. Rev. B 46, 1321 (1992). O 2 p Hybridized w. Ti 4 p, Ti 3 d Ti- 3 p

ONE SOLUTION Electronic Structure E Ti 3 d / O 2 p EF O 2 p Hybridized w. Ti 4 p, Ti 3 d Treat all the states in a single energy window: • Automatically orthogonal. • Need to add variational freedom. • Could invent quadratic or cubic APW methods. (r) = -1/2 { (A lm Ti- 3 p c. G ei(G+k) r G lmul(r)+Blmůl(r)+Clmül(r)) Ylm(r) Problem: This requires an extra matching condition, e. g. second derivatives continuous method will be impractical due to the high planewave cut-off needed.

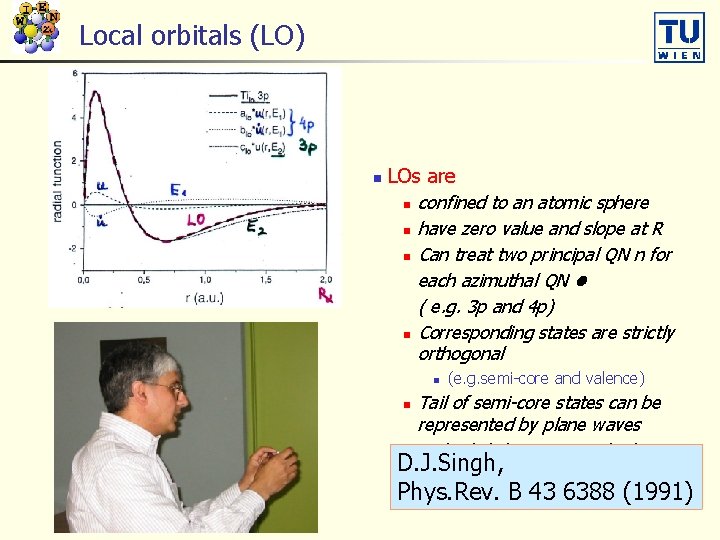
Local orbitals (LO) n LOs are n confined to an atomic sphere n have zero value and slope at R n Can treat two principal QN n for each azimuthal QN ( e. g. 3 p and 4 p) n Corresponding states are strictly orthogonal n (e. g. semi-core and valence) Tail of semi-core states can be represented by plane waves n Only slightly increases the basis set D. J. Singh, (matrix size) n Phys. Rev. B 43 6388 (1991)

THE LAPW+LO METHOD Key Points: 1. The local orbitals should only be used for those atoms and angular momenta where they are needed. 2. The local orbitals are just another way to handle the augmentation. They look very different from atomic functions. 3. We are trading a large number of extra planewave coefficients for some clm. Shape of H and S <G|G>

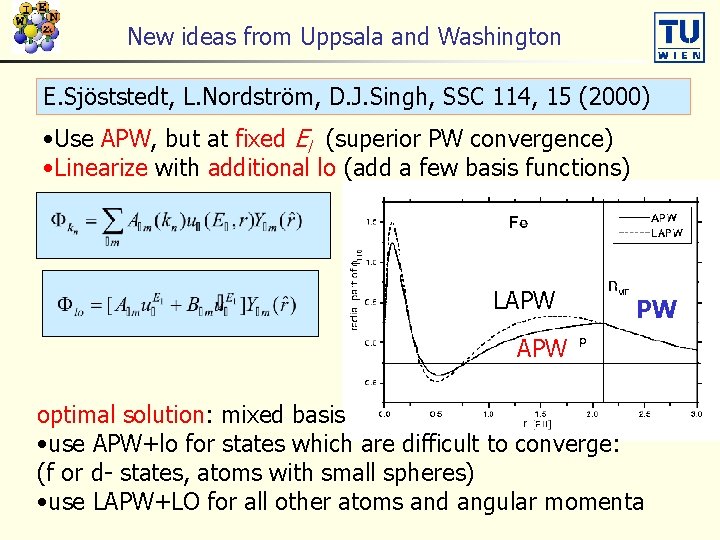
New ideas from Uppsala and Washington E. Sjöststedt, L. Nordström, D. J. Singh, SSC 114, 15 (2000) • Use APW, but at fixed El (superior PW convergence) • Linearize with additional lo (add a few basis functions) LAPW PW APW optimal solution: mixed basis • use APW+lo for states which are difficult to converge: (f or d- states, atoms with small spheres) • use LAPW+LO for all other atoms and angular momenta

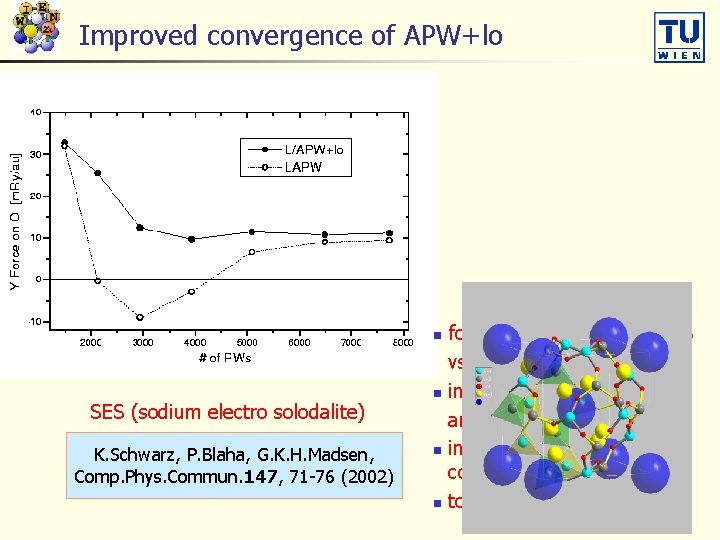
Improved convergence of APW+lo force (Fy) on oxygen in SES vs. # plane waves n in LAPW changes sign and converges slowly n in APW+lo better convergence n to same value as in LAPW n SES (sodium electro solodalite) K. Schwarz, P. Blaha, G. K. H. Madsen, Comp. Phys. Commun. 147, 71 -76 (2002)

Relativistic effects For example: Ti n Valences states n Scalar relativistc n n mass-velocity Darwin s-shift Spin orbit coupling on demand by second variational treatment Semi-core states n Scalar relativistic n No spin orbit coupling n on demand n n n spin orbit coupling by second variational treatment Additional local orbital (see Th-6 p 1/2) Core states n Full relativistic n Dirac equation

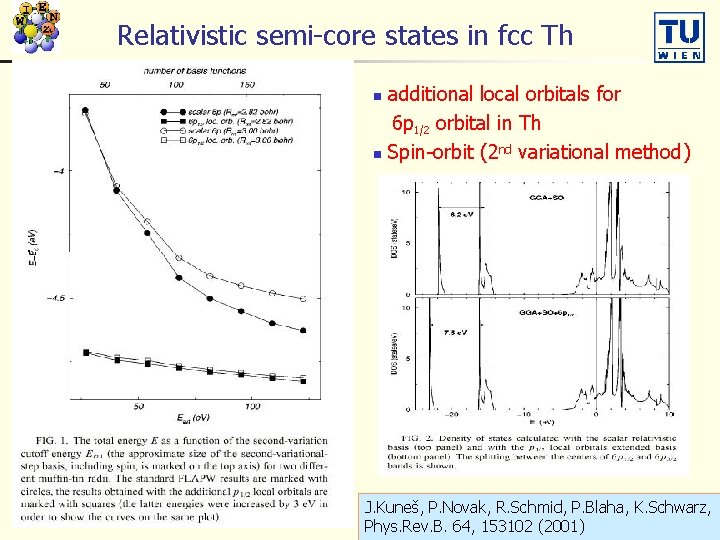
Relativistic semi-core states in fcc Th additional local orbitals for 6 p 1/2 orbital in Th n Spin-orbit (2 nd variational method) n J. Kuneš, P. Novak, R. Schmid, P. Blaha, K. Schwarz, Phys. Rev. B. 64, 153102 (2001)

(L)APW methods APW + local orbital method (linearized) augmented plane wave method Total wave function n… 50 -100 PWs /atom Variational method: spin polarization n shift of d-bands problem n Generalized eigenvalue n Lower Hubbard band (spin up) n Upper Hubbard band (spin down)

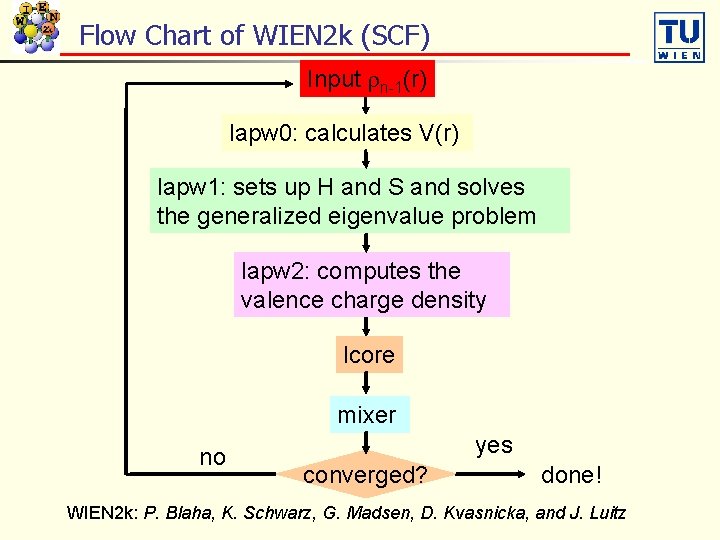
Flow Chart of WIEN 2 k (SCF) Input n-1(r) lapw 0: calculates V(r) lapw 1: sets up H and S and solves the generalized eigenvalue problem lapw 2: computes the valence charge density lcore mixer no yes converged? done! WIEN 2 k: P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka, and J. Luitz

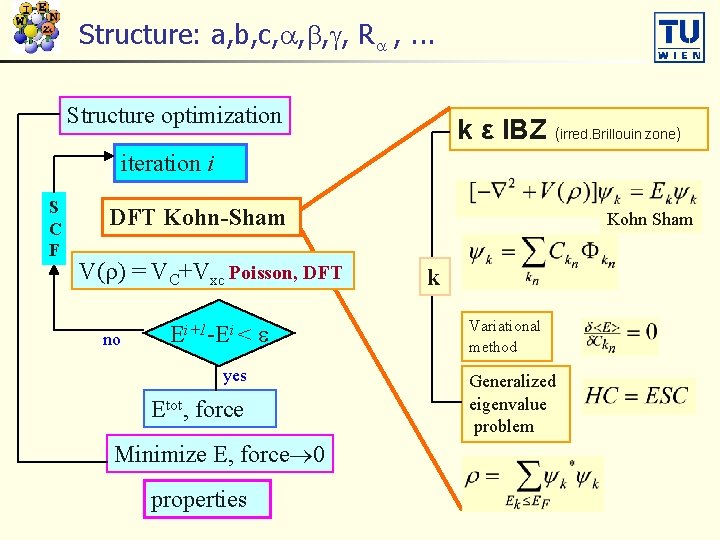
Structure: a, b, c, , R , . . . Structure optimization k ε IBZ (irred. Brillouin zone) iteration i S C F DFT Kohn-Sham V( ) = VC+Vxc Poisson, DFT no Ei+1 -Ei < yes Etot, force Minimize E, force 0 properties Kohn Sham k Variational method Generalized eigenvalue problem

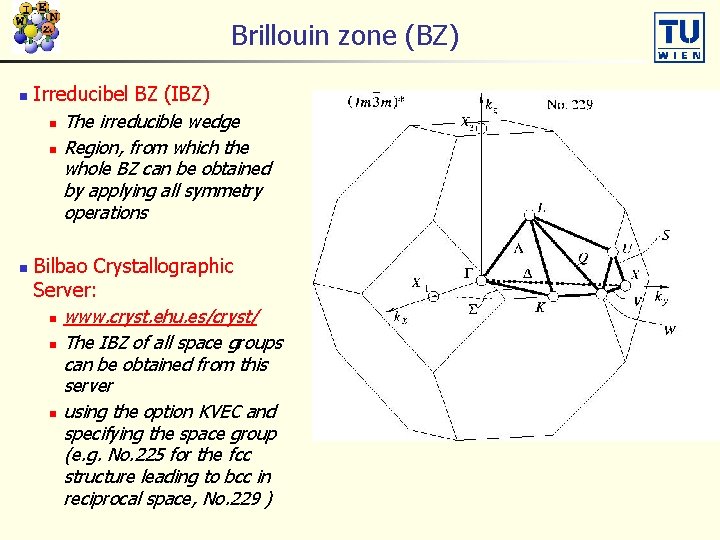
Brillouin zone (BZ) n n Irreducibel BZ (IBZ) n The irreducible wedge n Region, from which the whole BZ can be obtained by applying all symmetry operations Bilbao Crystallographic Server: n www. cryst. ehu. es/cryst/ n The IBZ of all space groups can be obtained from this server n using the option KVEC and specifying the space group (e. g. No. 225 for the fcc structure leading to bcc in reciprocal space, No. 229 )

WIEN 2 k software package An Augmented Plane Wave Plus Local Orbital Program for Calculating Crystal Properties Peter Blaha Karlheinz Schwarz Georg Madsen Dieter Kvasnicka Joachim Luitz November 2001 Vienna, AUSTRIA Vienna University of Technology

The WIEN 2 k authors

Development of WIEN 2 k n Authors of WIEN 2 k P. Blaha, K. Schwarz, D. Kvasnicka, G. Madsen and J. Luitz Other contributions to WIEN 2 k n C. Ambrosch-Draxl (Univ. Graz, Austria), optics n U. Birkenheuer (Dresden), wave function plotting n R. Dohmen und J. Pichlmeier (RZG, Garching), parallelization n R. Laskowski (Vienna), non-collinear magnetism n P. Novák and J. Kunes (Prague), LDA+U, SO n B. Olejnik (Vienna), non-linear optics n C. Persson (Uppsala), irreducible representations n M. Scheffler (Fritz Haber Inst. , Berlin), forces, optimization n D. J. Singh (NRL, Washington D. C. ), local orbitals (LO), APW+lo n E. Sjöstedt and L Nordström (Uppsala, Sweden), APW+lo n J. Sofo (Penn State, USA), Bader analysis n B. Yanchitsky and A. Timoshevskii (Kiev), space group n and many others …. n

International co-operations n More than 500 user groups worldwide 25 industries (Canon, Eastman, Exxon, Fuji, A. D. Little, Mitsubishi, Motorola, NEC, Norsk Hydro, Osram, Panasonic, Samsung, Sony, Sumitomo). n Europe: (ETH Zürich, MPI Stuttgart, Dresden, FHI Berlin, DESY, TH Aachen, ESRF, Prague, Paris, Chalmers, Cambridge, Oxford) n America: ARG, BZ, CDN, MX, USA (MIT, NIST, Berkeley, Princeton, Harvard, Argonne NL, Los Alamos Nat. Lab. , Penn State, Georgia Tech, Lehigh, Chicago, SUNY, UC St. Barbara, Toronto) n far east: AUS, China, India, JPN, Korea, Pakistan, Singapore, Taiwan (Beijing, Tokyo, Osaka, Sendai, Tsukuba, Hong Kong) n n Registration at www. wien 2 k. at 400/4000 Euro for Universites/Industries n code download via www (with password), updates, bug fixes, news n User’s Guide, faq-page, mailing-list with help-requests n