Density Functional Theory a first look Patrick Briddon

Density Functional Theory: a first look Patrick Briddon Theory of Condensed Matter Department of Physics, University of Newcastle, UK.

Contents Density Functional Theory – Hohenberg Kohn Theorems – Thomas Fermi Theory – Kohn-Sham Equations – Self Consistency – Approximations for Exc.

Density Functional Theory Work with n(r) instead of Standard approach of QM : DFT : work in terms of density : N. B. : few IFs and BUTs here

3 Important Questions Three important questions: • Can we really write E[n]? • If so, how can we find n(r)? • What is the functional E[n] ?

1 st Hohenberg Kohn Theorem The external potential V(r) is determined to within a constant by the ground state charge density of a system. i. e. one-to-one relationship This is an astonishing statement! Why?

1 st Hohenberg Kohn Theorem Proof: Suppose we have two systems Hamiltonians H 1, H 2 External potentials V 1 , V 2 GS wavefunctions: 1, 2 But the same GS density n(r)

We clearly have But: So: Swap 1 and 2: Contradiction!

Our starting point was wrong! We cannot have two different systems with the same GS density. Importance of this: we can write E[n]. Now move on the second question – how can we find the density? Hohenberg – Kohn’s second theorem.

2 nd Hohenberg Kohn Theorem “The true ground state charge density is that which minimises the total energy. ” An equivalent to the usual variational principle of quantum mechanics.

Proof We have (variational principle) Define Then

Some problems V-representability (only minimise over densities which can arise from GS wavefunctions of real systems Levy showed that the densities need only satisfy a weaker condition that they can be obtained from an antisymmetric wavefunction (N-representable). n must be +ve, continuous, normalised

Some extensions Spin dependent potentials e. g. magnetic fields E[n] E[n, n - n ] or E[n , n ] Main advantage: better description of open shell systems.

3 Important Questions Three important questions: • Can we really write E[n]? • If so, how can we find n(r)? • What is the functional E[n] ? Now for the last question. What is the formula!

What is the functional? Difficult : still not answered exactly! Problem is that other two terms are very large - any attempt at approximation must be good.

Thomas-Fermi Method Classical expression for electron term:

Thomas-Fermi Method Statistical idea for KE based on uniform electron gas result: KE per electron =

Thomas-Fermi Method What about a non uniform system? A. Assume that things vary slowly: DV r Total is thus

Thomas-Fermi Method Final energy is thus: How useful is this?

Thomas-Fermi Method What is the conclusion? • Energies quite good (error < 1%). • Difference of energies not good enough to describe bonding. • How can we improve this?

Thomas-Fermi Method Add exchange/correlation (missing do far). • Try to take account of non-uniform system. • Write T[n] as T[n, grad |n|] • All failures!

Kohn-Sham method Phys Rev 140, 1133 A (1966) Realised that approximation must be made to terms that are small: KE is big! Improving T[n] did not work. Need a completely different approach. Second half of HK paper therefore discarded.

Kohn-Sham method Phys Rev 140, 1133 A (1966) Introduce a system which: 1. Is non-interacting 2. Has same n(r) as the real system. [non-interacting N-representability - an assumption! ]

Kohn-Sham contd. where Ts[n] is the KE of the non-interacting system and the final term, T, is small.

Kohn-Sham contd. Exc[n] includes both T and contributions to el-el energy beyond the Hartree term. The key hope is that this is • small • less sensitive to external potential These mean differences are accurate.

We now have two questions: (a) how to find Ts[n] ? (b) what is Exc[n] ? For a non-interacting system it is exactly true that the many electron wavefunction is a single Slater determinant.

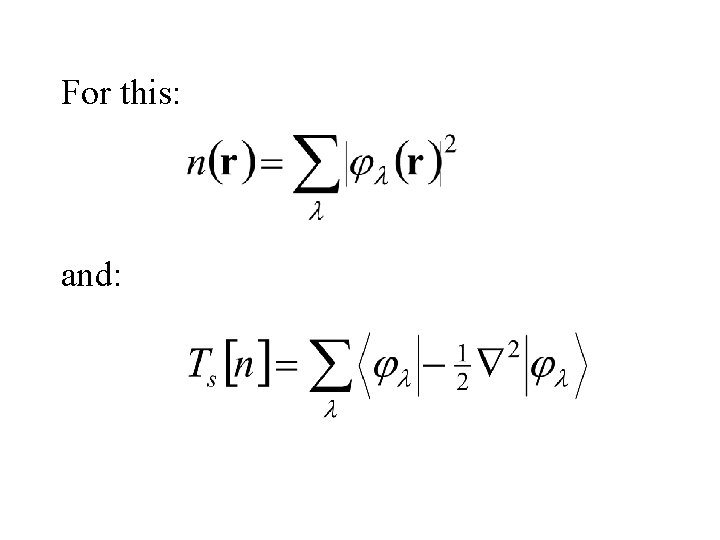
For this: and:

The (r) must be found from a self consistent solution of: These are called the Kohn-Sham equations. Solve iteratively:

Guess: Construct Solve Find new density: Look at Form a better input and continue.

Self Consistent Cycle • This process is called the self-consistent cycle. • Starting guess is a superposition of atomic charge densities (or a restart dump). • AIMPRO produces output showing how the energy converged and how the input and output densities come together.

AIMPRO SCF etot, echerr etot, echerr 1 2 3 4 5 -1. 1289007706 -1. 1319461182 -1. 1361047998 -1. 1360826939 -1. 1361076063 0. 0547166884 0. 0303263020 0. 0000338275 0. 0001723143 0. 0000002649 0. 884981 0. 488911 0. 000689 0. 002700 0. 000004 2. 95 3. 00 2. 99 3. 00 106. 1 120. 7 The numbers are: • Total energy (reduces to converged value) • 2 measures of • Time taken per iteration • Current memory being used (MB) • Max memory used so far (MB)

Kohn-Sham Levels We got the Kohn Sham eqn: Q: what exactly are the e and ? A: the eigenvalues and eigenfunctions of a ficticious non-interacting system which has the same density as the real system.

KS Levels Contd. They are not the energies of quasiparticles. Typical semiconductor results: Lattice constant to 1% Bulk modulus to 1% Phonon frequencies to 5% LDA “gap” for Si is 0. 6 e. V; 0. 1 e. V for Ge!

KS Levels Contd. Bandstructures are qualitatively correct. (Scissors operator). Physical nature of the KS eigenfunctions sensible. P in Si - get state just below conduction band Dangling bonds - localised states in mid gap.

AIMPRO and KS levels spin, kpoint : 1 -10. 0938 2. 0000 1 1. 2658 0. 0000 1 3. 7422 0. 0000 5. 9056 0. 0000 8. 7912 0. 0000 The KS levels in e. V. Used in “bandstructure” plots. Occupancies also given (this is a spin averaged calculation)

3 Important Questions Three important questions: • Can we really write E[n]? • If so, how can we find n(r)? • What is the functional E[n] ? • All remaining questions are in Exc[n]. Now finally we look at what this is.

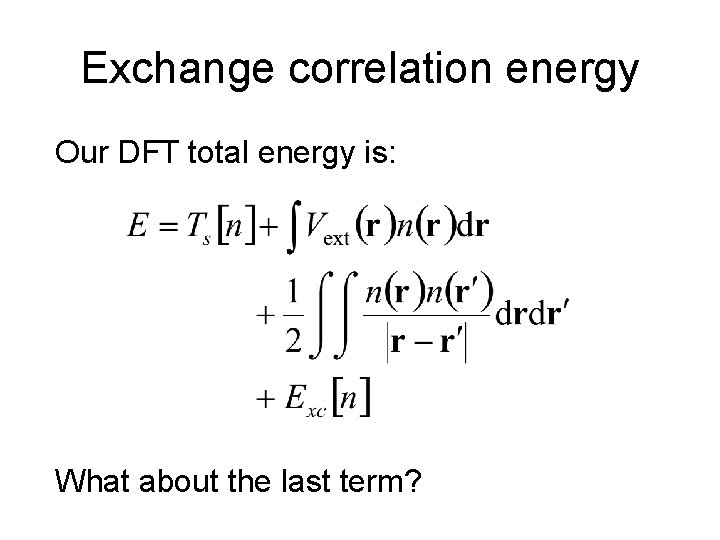
Exchange correlation energy Our DFT total energy is: What about the last term?

The Local Density Approximation (LDA) Write where exc(n) is the exchange-correlation energy per electron for a uniform electron gas. This seems a bit rough and very similar to Thomas Fermi, but this term is now very much smaller.

Exc for Homogeneous electron gas • By simple analytical treatment for the exchange energy. • Using many body perturbation theory (for various limits of correlation energy) • By looking at quantum Monte-Carlo calculations and parametrising them • Intelligent interpolation between these

Exc for Homogeneous electron gas contd. Simple analysis for exchange part gives Correlation is harder, see: : • Perdew Zunger (1981) • Vosko, Wilk, Nusair (1980) • Perdew, Wang (1992)

Simple Tests : Molecules Example : water H 20

Simple tests : solids • Standard “bulk” calculations : – lattice constant (Si : 1%) – bulk modulus (Si : 2%) – phonon spectra (2 %) – formation energies (LDA : 20 %) – excitation energies (50 %)

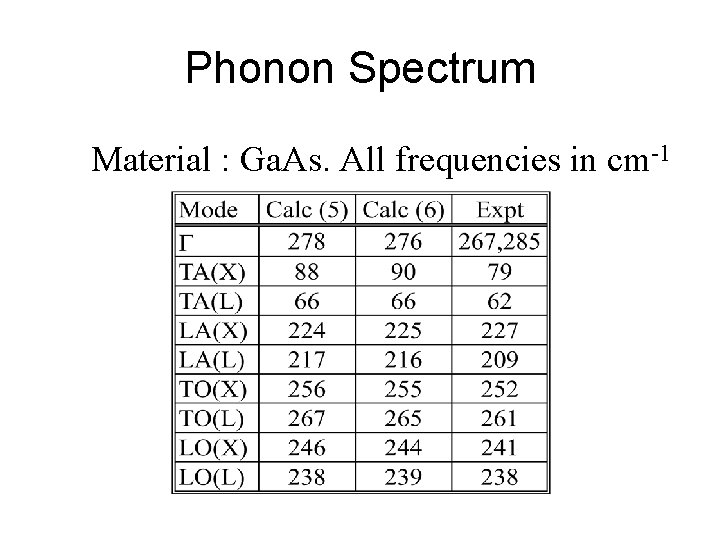
Phonon Spectrum Material : Ga. As. All frequencies in cm-1

How to Improve? Next step is to move beyond the LDA: The Gradient expansion Approximation (GEA). Early history of these was bad. Calculations made worse, not better.

Generalised Gradient Approximations (GGA) Idea is to ensure that • Sum rules are obeyed correctly • scaling behaviour of exchange correlation energy correct • Various limiting forms • Bounds (Lieb-Oxford)

Popular GGAs • • B 88 (empirical, chemistry) BLYP (chemistry) PW 91 (physics, poor form) PBE 96 (physics, easier to use)

Atomisation energies (kcal/mol) (1 e. V = 23 kcal/mol)

Generalised Gradient Approximations (GGA) In general, GGA weakens bonds slightly. It improves results for: • binding energies of molecules • description of surfaces • H-bonding

THE CONCLUSION • An absolutely huge success • 1988 two groups in UK doing DFT – Cambridge (TCM) – Exeter • Today: every department? • Chemistry/engineering too! • Applications in huge variety of areas.

Work to do! • • • Kittel Ch 6: “Free Electron Fermi Gas” Hohenberg and Kohn, PR (1964) Kohn-Sham, PR (1965) Perdew Zunger, PRB (1981) Perdew, Wang, PRB (1992) Perdew, Burke, Enzerhoff PRL (1996)