Dense Subgraphs with Restrictions Applications to Gene Annotations

Dense Subgraphs with Restrictions & Applications to Gene Annotations Graphs Samir Khuller University of Maryland Joint Work with Barna Saha, Allie Hoch, Louiqa Raschid, Xiao-Ning Zhang RECOMB 2010

Sitting in a talk on community detection…. . How do we define a community? Perhaps we want to capture a group of individuals with strong interactions within the group?

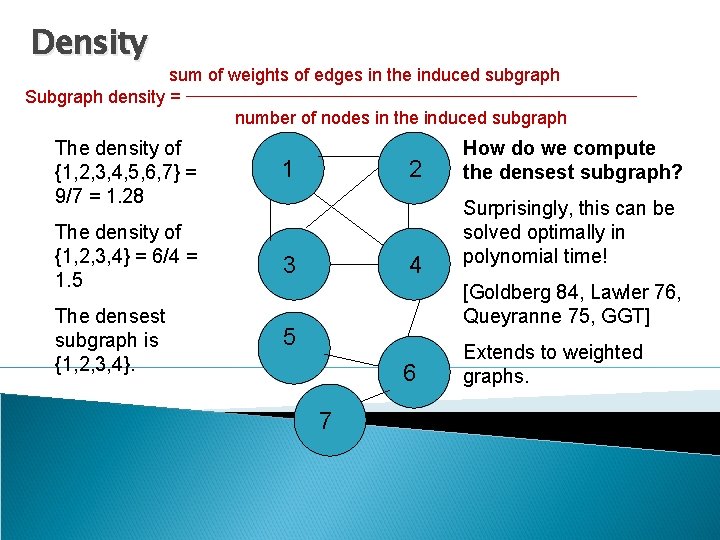
Density sum of weights of edges in the induced subgraph Subgraph density = number of nodes in the induced subgraph The density of {1, 2, 3, 4, 5, 6, 7} = 9/7 = 1. 28 11 The density of {1, 2, 3, 4} = 6/4 = 1. 5 3 The densest subgraph is {1, 2, 3, 4}. 5 2 4 How do we compute the densest subgraph? Surprisingly, this can be solved optimally in polynomial time! [Goldberg 84, Lawler 76, Queyranne 75, GGT] 6 7 Extends to weighted graphs.

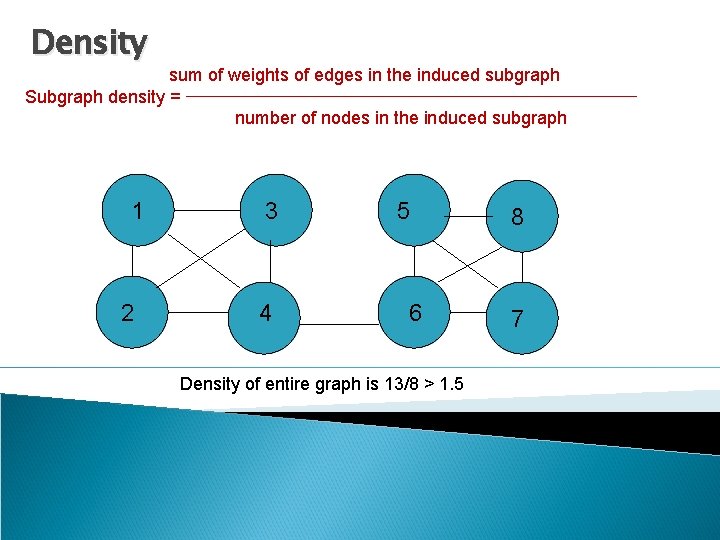
Density sum of weights of edges in the induced subgraph Subgraph density = number of nodes in the induced subgraph 1 2 3 4 5 6 Density of entire graph is 13/8 > 1. 5 8 7

Are Dense Subgraphs Useful? Are all dense subgraphs meaningful ? ◦ How do we allow some control over the kind of dense subgraphs that are found? ◦ Putting size constraints makes the problem intractable immediately. Densest subgraph of size >=k. NP-hard, 2 approximation [Anderson][Khuller, Saha]. Greedily Union densest subgraphs…. . Densest subgraph of size <=k (or =k). NP-hard and some approximations known [Feige, Kortsarz, Peleg] [Charikar et al].

Goldberg’s algorithm: a new flow network, is created with “directed” edges. ◦ An s-t min cut is computed in order to find the densest subgraph after guessing the max density. Nodes on the “s” side of the cut are part of a densest subgraph. ◦ GGT speeds everything up to a single flow computation! Lawler’s algorithm: slightly different flow construction, more intuitive. Greedy algorithm: recursively delete low degree nodes. Gives a 2 approximation to density! Fast!

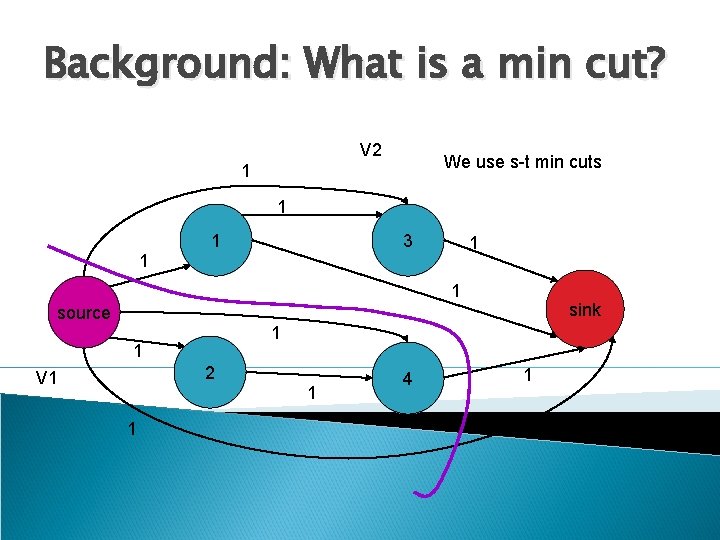
Background: What is a min cut? V 2 We use s-t min cuts 1 1 1 3 1 1 1 sink source 1 1 2 V 1 1 1 4 1

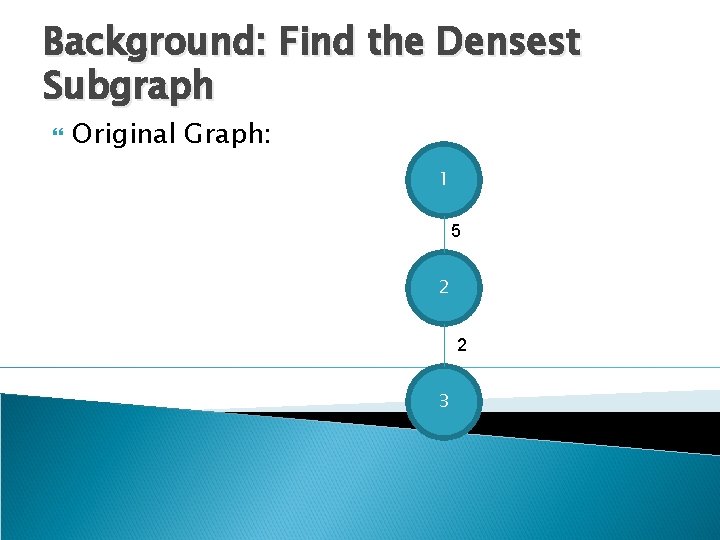
Background: Find the Densest Subgraph Original Graph: 1 5 2 2 3

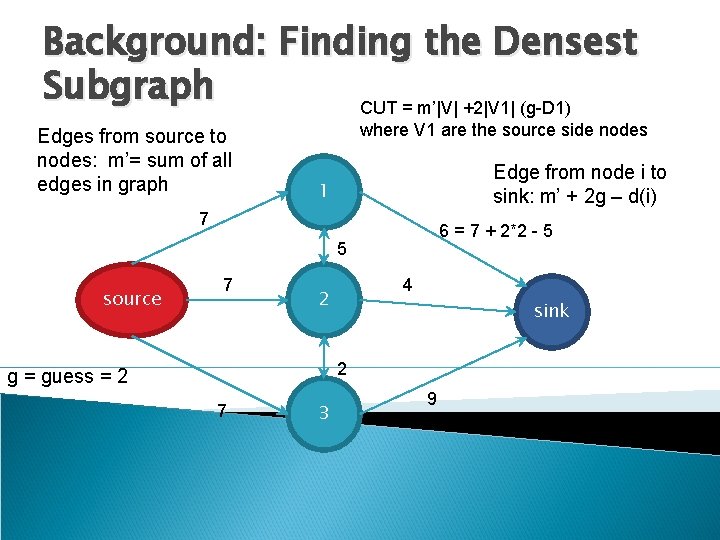
Background: Finding the Densest Subgraph CUT = m’|V| +2|V 1| (g-D 1) Edges from source to nodes: m’= sum of all edges in graph where V 1 are the source side nodes Edge from node i to sink: m’ + 2 g – d(i) 1 7 6 = 7 + 2*2 - 5 5 source 7 4 2 sink 2 g = guess = 2 7 3 9

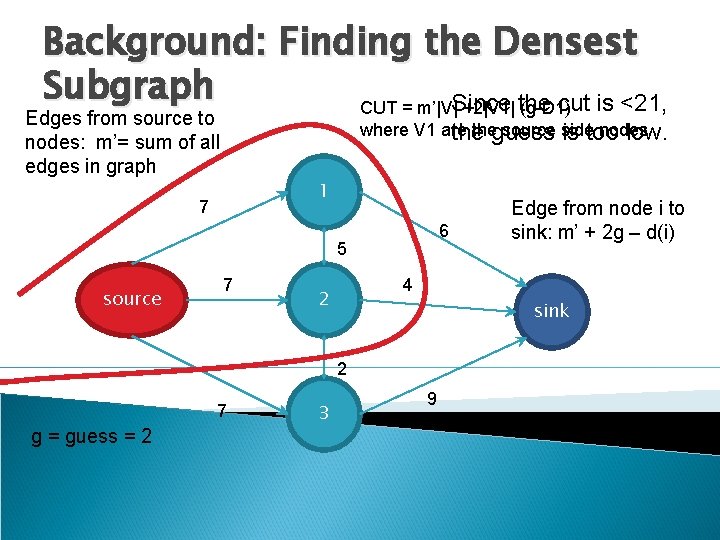
Background: Finding the Densest Subgraph cut is <21, CUT = m’|V|Since +2|V 1| the (g-D 1) Edges from source to nodes: m’= sum of all edges in graph where V 1 are theguess source side nodes the is too low. 1 7 6 5 source 7 4 2 sink 2 7 g = guess = 2 3 Edge from node i to sink: m’ + 2 g – d(i) 9

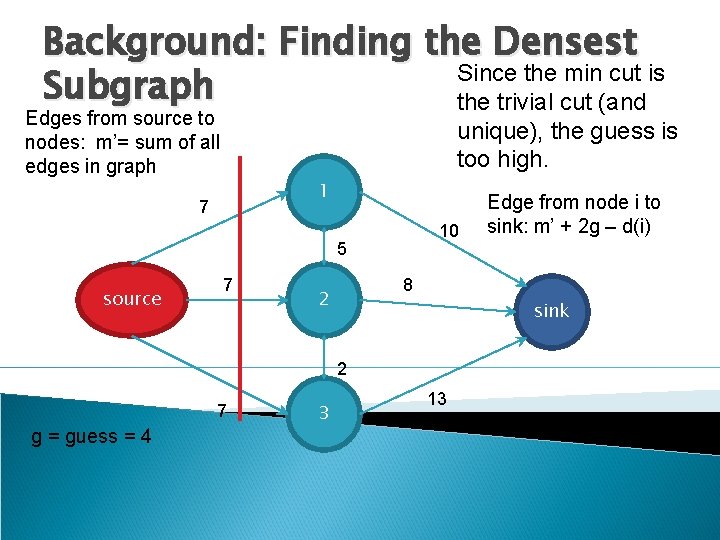
Background: Finding the Densest Since the min cut is Subgraph the trivial cut (and Edges from source to nodes: m’= sum of all edges in graph unique), the guess is too high. 1 7 10 5 source 7 8 2 sink 2 7 g = guess = 4 3 Edge from node i to sink: m’ + 2 g – d(i) 13

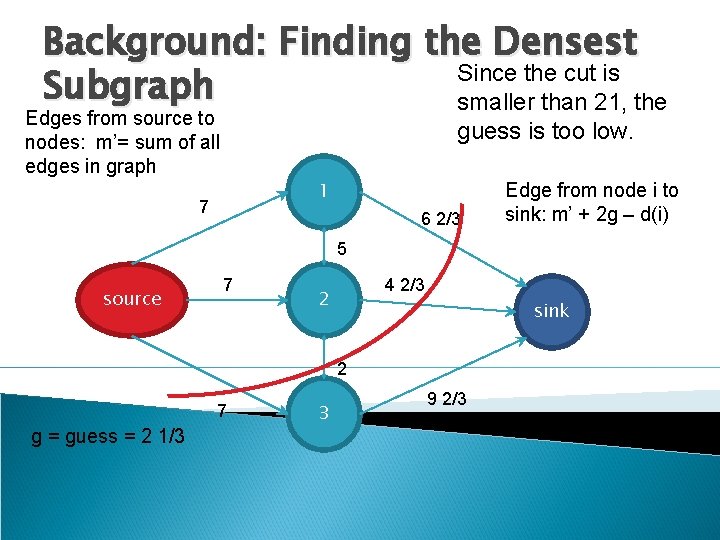
Background: Finding the Densest Since the cut is Subgraph smaller than 21, the Edges from source to nodes: m’= sum of all edges in graph guess is too low. 1 7 6 2/3 Edge from node i to sink: m’ + 2 g – d(i) 5 source 7 4 2/3 2 sink 2 7 g = guess = 2 1/3 3 9 2/3

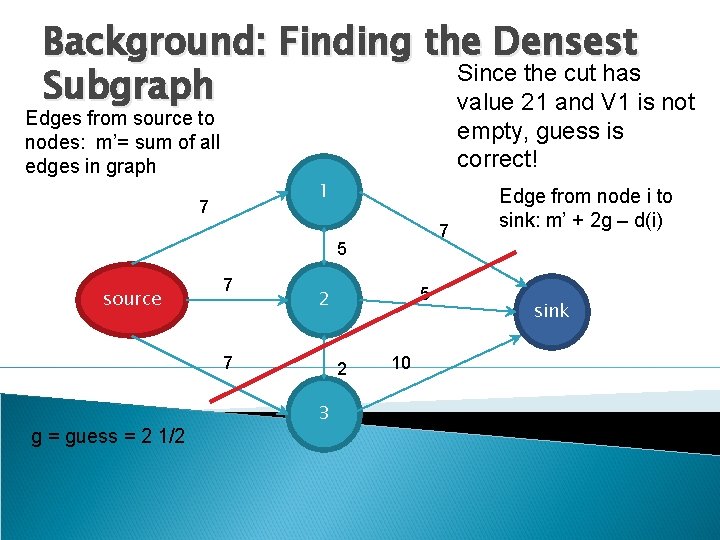
Background: Finding the Densest Since the cut has Subgraph value 21 and V 1 is not Edges from source to nodes: m’= sum of all edges in graph empty, guess is correct! 1 7 7 5 source 7 7 g = guess = 2 1/2 5 2 2 3 10 Edge from node i to sink: m’ + 2 g – d(i) sink

What can we do with this weapon? Consider gene annotation data from TAIR. For large networks we can use the fast greedy approximation (gave us the densest subgraph every time!).

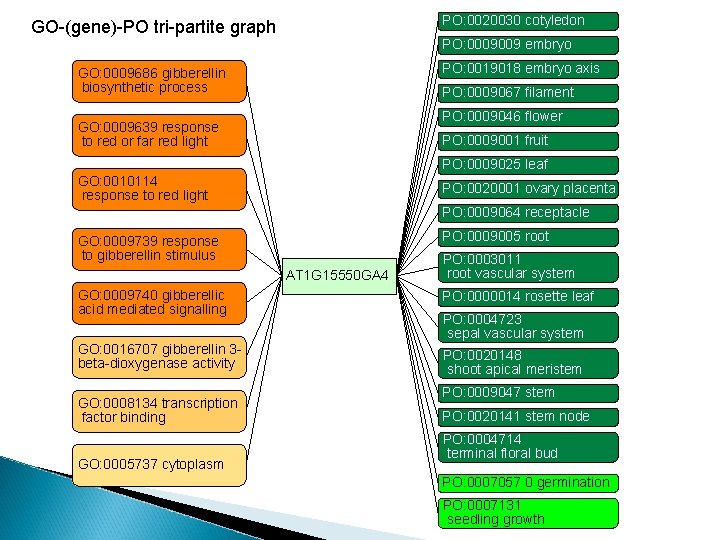
PO: 0020030 cotyledon GO-(gene)-PO tri-partite graph PO: 0009009 embryo PO: 0019018 embryo axis GO: 0009686 gibberellin biosynthetic process PO: 0009067 filament PO: 0009046 flower GO: 0009639 response to red or far red light PO: 0009001 fruit PO: 0009025 leaf GO: 0010114 response to red light PO: 0020001 ovary placenta PO: 0009064 receptacle PO: 0009005 root GO: 0009739 response to gibberellin stimulus AT 1 G 15550 GA 4 PO: 0003011 root vascular system GO: 0009740 gibberellic acid mediated signalling PO: 0000014 rosette leaf GO: 0016707 gibberellin 3 beta-dioxygenase activity PO: 0020148 shoot apical meristem GO: 0008134 transcription factor binding GO: 0005737 cytoplasm PO: 0004723 sepal vascular system PO: 0009047 stem PO: 0020141 stem node PO: 0004714 terminal floral bud PO: 0007057 0 germination PO: 0007131 seedling growth

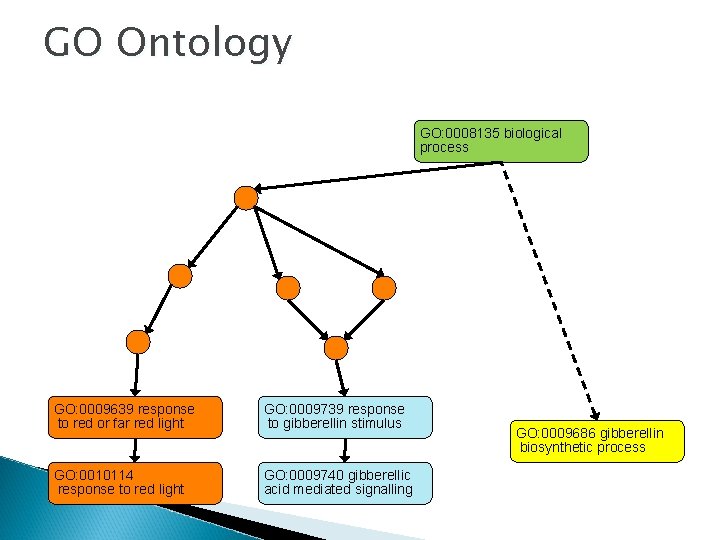
GO Ontology GO: 0008135 biological process GO: 0009639 response to red or far red light GO: 0009739 response to gibberellin stimulus GO: 0010114 response to red light GO: 0009740 gibberellic acid mediated signalling GO: 0009686 gibberellin biosynthetic process

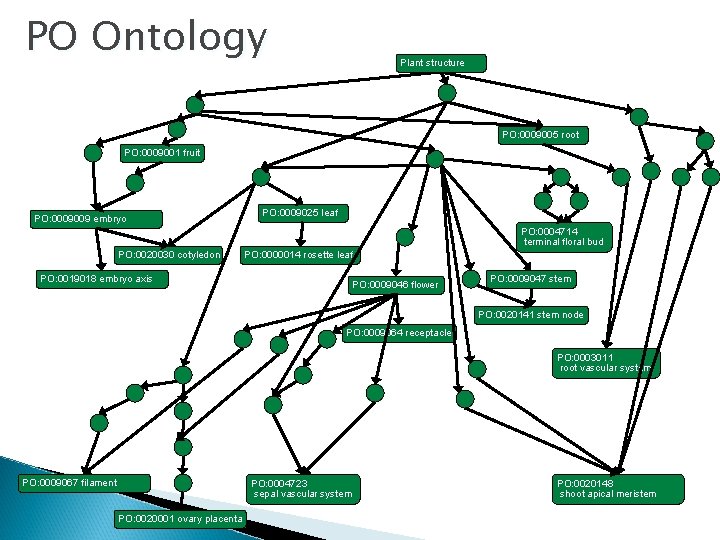
PO Ontology Plant structure PO: 0009005 root PO: 0009001 fruit PO: 0009009 embryo PO: 0009025 leaf PO: 0004714 terminal floral bud PO: 0020030 cotyledon PO: 0000014 rosette leaf PO: 0019018 embryo axis PO: 0009046 flower PO: 0009047 stem PO: 0020141 stem node PO: 0009064 receptacle PO: 0003011 root vascular system PO: 0009067 filament PO: 0004723 sepal vascular system PO: 0020001 ovary placenta PO: 0020148 shoot apical meristem

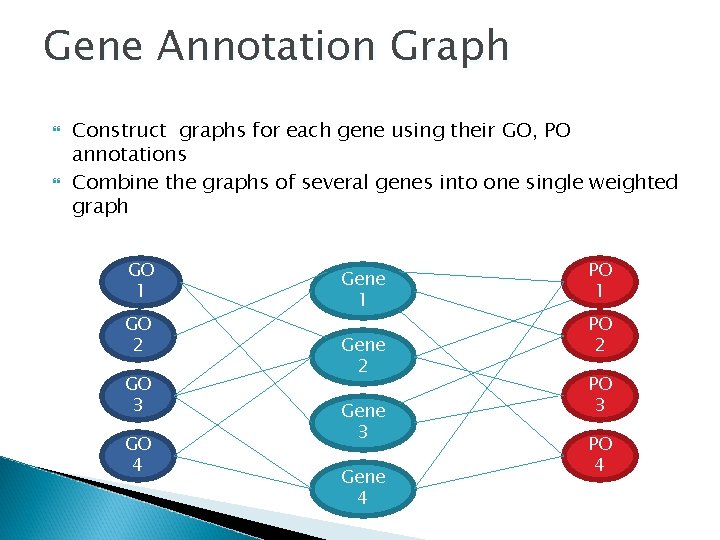
Gene Annotation Graph Construct graphs for each gene using their GO, PO annotations Combine the graphs of several genes into one single weighted graph GO 1 GO 2 GO 3 GO 4 Gene 1 Gene 2 Gene 3 Gene 4 PO 1 PO 2 PO 3 PO 4

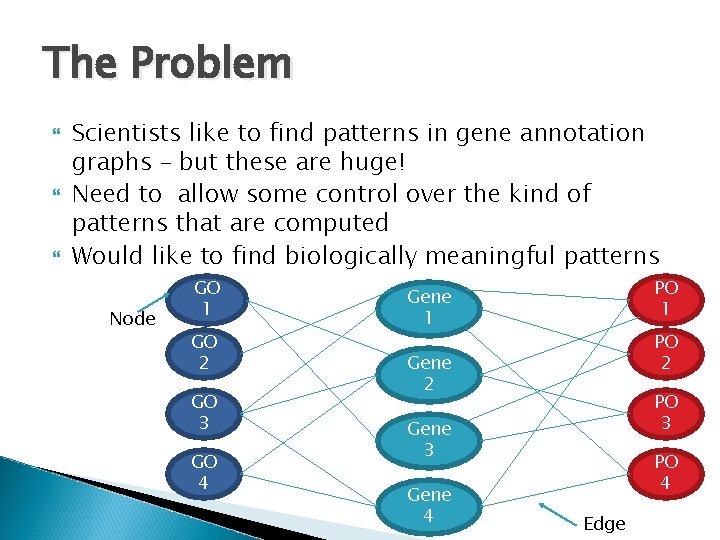
The Problem Scientists like to find patterns in gene annotation graphs – but these are huge! Need to allow some control over the kind of patterns that are computed Would like to find biologically meaningful patterns Node GO 1 GO 2 GO 3 GO 4 PO 1 Gene 1 PO 2 Gene 2 PO 3 Gene 4 PO 4 Edge

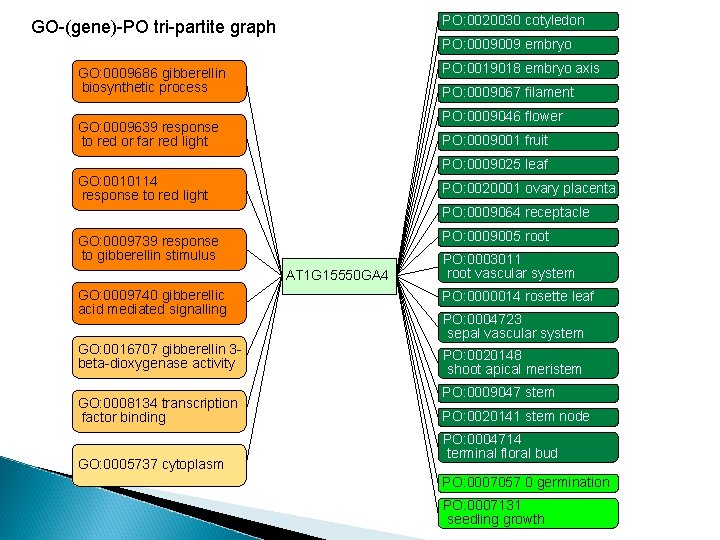
PO: 0020030 cotyledon GO-(gene)-PO tri-partite graph PO: 0009009 embryo PO: 0019018 embryo axis GO: 0009686 gibberellin biosynthetic process PO: 0009067 filament PO: 0009046 flower GO: 0009639 response to red or far red light PO: 0009001 fruit PO: 0009025 leaf GO: 0010114 response to red light PO: 0020001 ovary placenta PO: 0009064 receptacle PO: 0009005 root GO: 0009739 response to gibberellin stimulus AT 1 G 15550 GA 4 PO: 0003011 root vascular system GO: 0009740 gibberellic acid mediated signalling PO: 0000014 rosette leaf GO: 0016707 gibberellin 3 beta-dioxygenase activity PO: 0020148 shoot apical meristem GO: 0008134 transcription factor binding GO: 0005737 cytoplasm PO: 0004723 sepal vascular system PO: 0009047 stem PO: 0020141 stem node PO: 0004714 terminal floral bud PO: 0007057 0 germination PO: 0007131 seedling growth

GO-PO bipartite graph GO: 0009686 gibberellin biosynthetic process GO: 0009639 response to red or far red light PO: 0020030 cotyledon PO: 0009009 embryo PO: 0019018 embryo axis PO: 0009067 filament PO: 0009046 flower PO: 0009001 fruit PO: 0009025 leaf GO: 0010114 response to red light PO: 0020001 ovary placenta PO: 0009064 receptacle GO: 0009739 response to gibberellin stimulus PO: 0009005 root GO: 0009740 gibberellic acid mediated signalling PO: 0000014 rosette leaf GO: 0016707 gibberellin 3 beta-dioxygenase activity PO: 0020148 shoot apical meristem GO: 0008134 transcription factor binding GO: 0005737 cytoplasm PO: 0003011 root vascular system PO: 0004723 sepal vascular system PO: 0009047 stem PO: 0020141 stem node PO: 0004714 terminal floral bud PO: 0007057 0 germination PO: 0007131 seedling growth

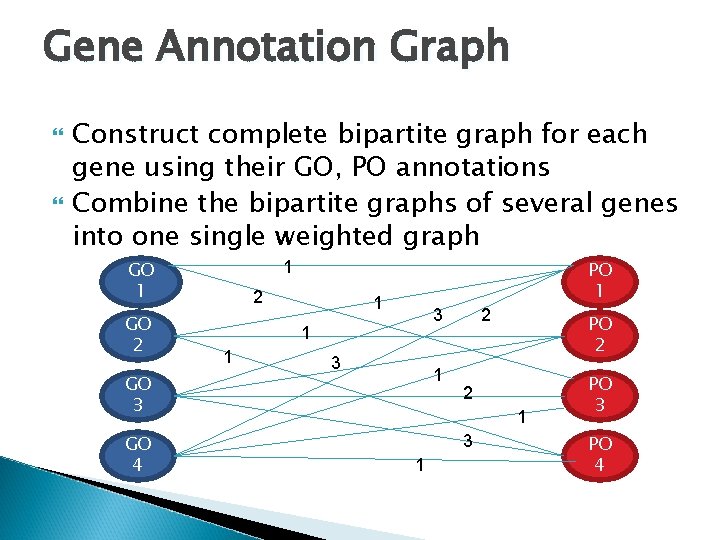
Gene Annotation Graph Construct complete bipartite graph for each gene using their GO, PO annotations Combine the bipartite graphs of several genes into one single weighted graph GO 1 GO 2 GO 3 GO 4 PO 1 1 2 1 3 1 2 PO 2 2 1 3 1 PO 3 PO 4

How can we extract knowledge? Cliques – these might give us some biological information – but this is a stringent reqmt. However clique finding is well known to be really hard (NP-hard, hard to approximate). Why not look for “dense regions”? Note that the notion of density could be defined for hyper-edges as well, but for our purposes this does not do as well.

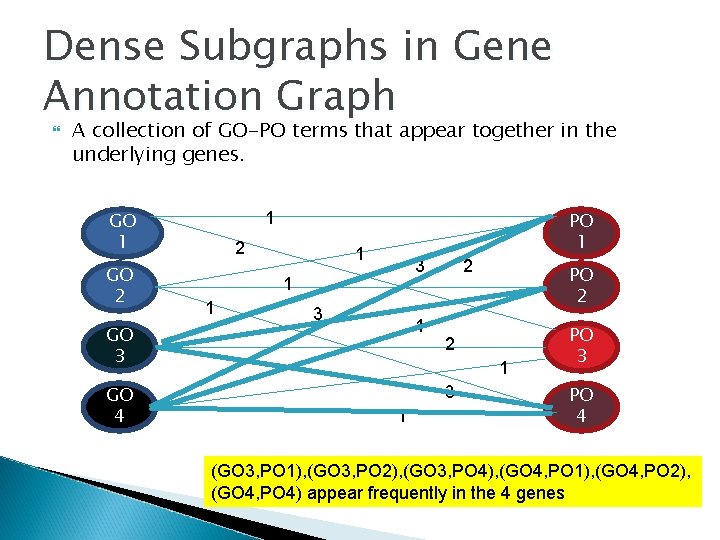
Dense Subgraphs in Gene Annotation Graph A collection of GO-PO terms that appear together in the underlying genes. GO 1 GO 2 GO 3 GO 4 PO 1 1 2 1 3 1 2 PO 2 2 1 3 1 PO 3 PO 4 (GO 3, PO 1), (GO 3, PO 2), (GO 3, PO 4), (GO 4, PO 1), (GO 4, PO 2), (GO 4, PO 4) appear frequently in the 4 genes

Biologically Meaningful Dense Subgraphs Are all dense subgraphs biologically meaningful ? ◦ How do we allow some control over the kind of dense subgraphs that are computed. ◦ In fact we can impose both restrictions at the same time! Distance Restricted Restrictions in dense subgraph computation GO terms and similarly PO terms that appear must be biologically related Subset Restricted Certain GO, PO terms must appear in the returned subgraph

Biologically Meaningful Dense Subgraphs Are all dense subgraphs biologically meaningful ? ◦ How do we allow some control over the kind of dense subgraphs that are found? Restrictions in dense subgraph computation Distance Restricted Subset Restricted GO terms that appear in the densest subgraph must be close in the GO ontology graph and similarly for the PO terms

Distance Restricted Subgraph Problem Distance threshold = 1 This means that some sets of nodes are not allowed to coexist in the final solution: {GO 1 , GO 2}, {GO 1, GO 4}, {PO 1 , PO 4}, {PO 1, PO 2}, {PO 2, PO 3, }. The final solution is {GO 2, GO 3, GO 4, PO 2, PO 4}, which has a density of. 8. GO 1 GO 4 GO 1 GO 2 GO 3 GO 4 PO 1 PO 2 PO 3 PO 4

Distance Restricted Subgraph Problem For arbitrary ontology graph structure ◦ NP Hard even to approximate it reasonably Reduction from Independent set problem ◦ Factor 2 relaxation of distance threshold is enough to get a solution with density as high as the optimum Trees, Interval Graphs, Each edge participates in small number of cycles ◦ Polynomial time algorithm to compute the optimum

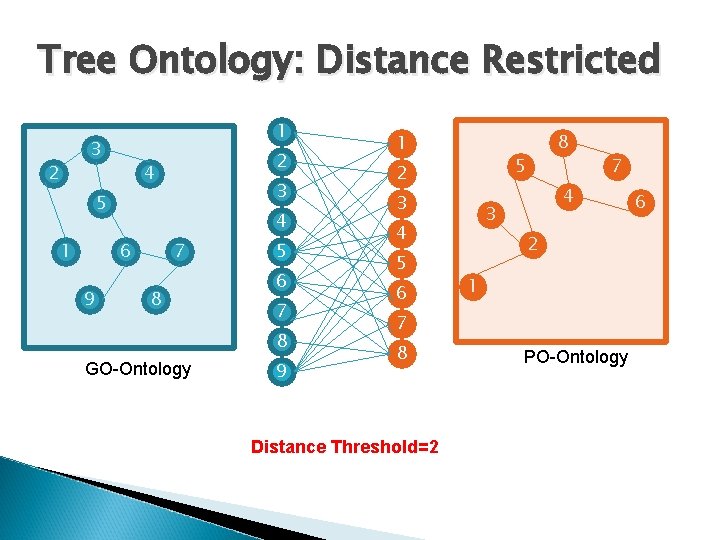
Tree Ontology: Distance Restricted 1 3 2 2 4 3 5 1 4 6 9 7 8 5 6 7 8 GO-Ontology 9 1 5 2 3 6 7 4 3 4 5 8 2 1 7 8 Distance Threshold=2 PO-Ontology 6

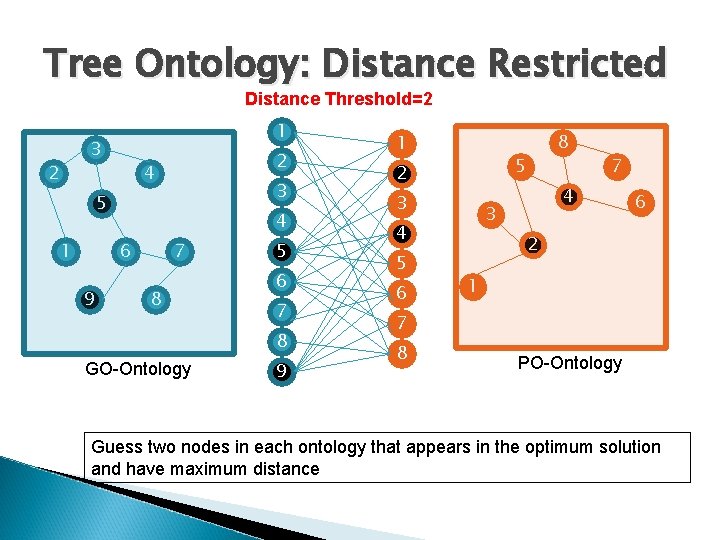
Tree Ontology: Distance Restricted Distance Threshold=2 1 3 2 2 4 3 5 1 4 6 9 7 8 5 6 7 8 GO-Ontology 9 1 5 2 3 6 7 4 3 4 5 8 6 2 1 7 8 PO-Ontology Guess two nodes in each ontology that appears in the optimum solution and have maximum distance

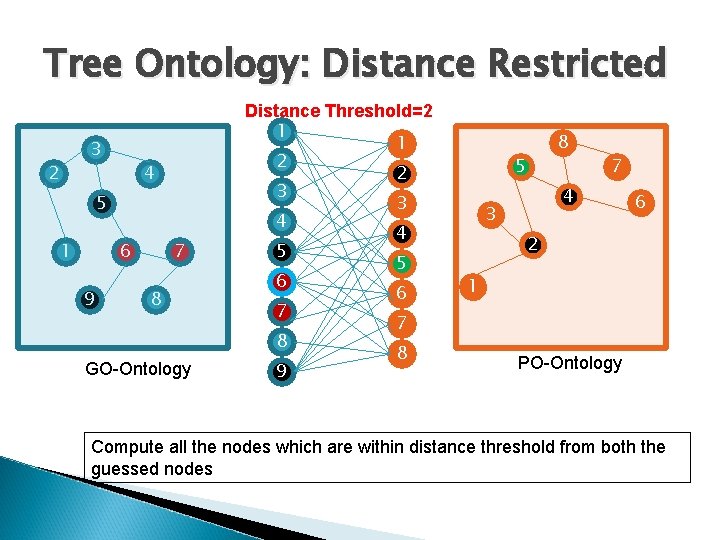
Tree Ontology: Distance Restricted 3 2 4 5 1 6 9 7 8 GO-Ontology Distance Threshold=2 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 8 5 7 4 3 6 2 1 PO-Ontology Compute all the nodes which are within distance threshold from both the guessed nodes

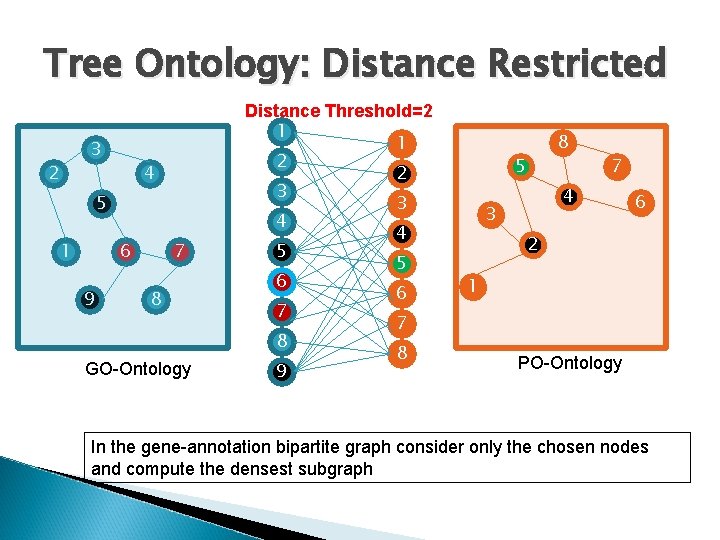
Tree Ontology: Distance Restricted 3 2 4 5 1 6 9 7 8 GO-Ontology Distance Threshold=2 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 8 5 7 4 3 6 2 1 PO-Ontology In the gene-annotation bipartite graph consider only the chosen nodes and compute the densest subgraph

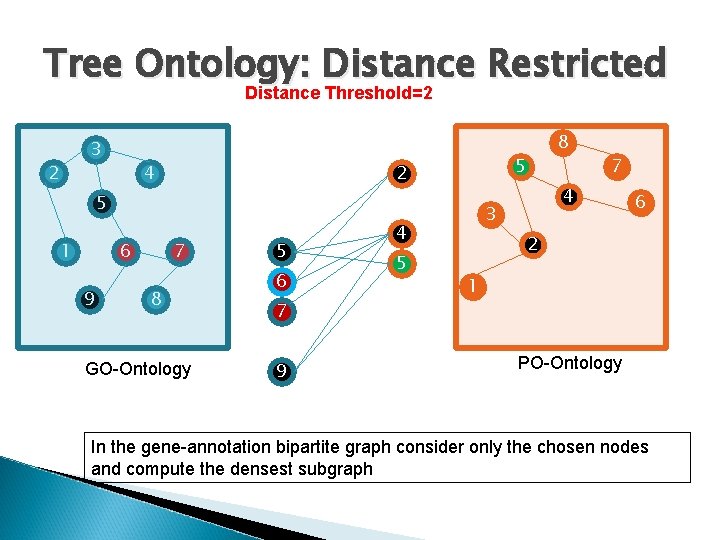
Tree Ontology: Distance Restricted Distance Threshold=2 3 2 4 5 2 5 1 6 9 7 8 GO-Ontology 5 6 7 9 7 4 3 4 5 8 6 2 1 PO-Ontology In the gene-annotation bipartite graph consider only the chosen nodes and compute the densest subgraph

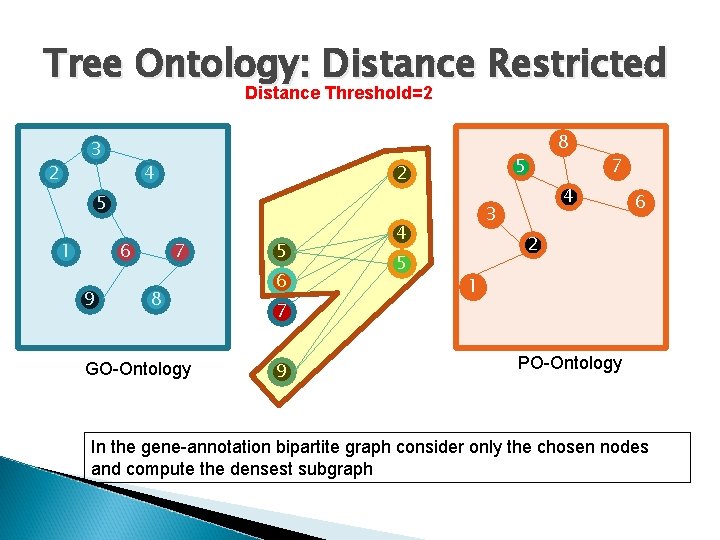
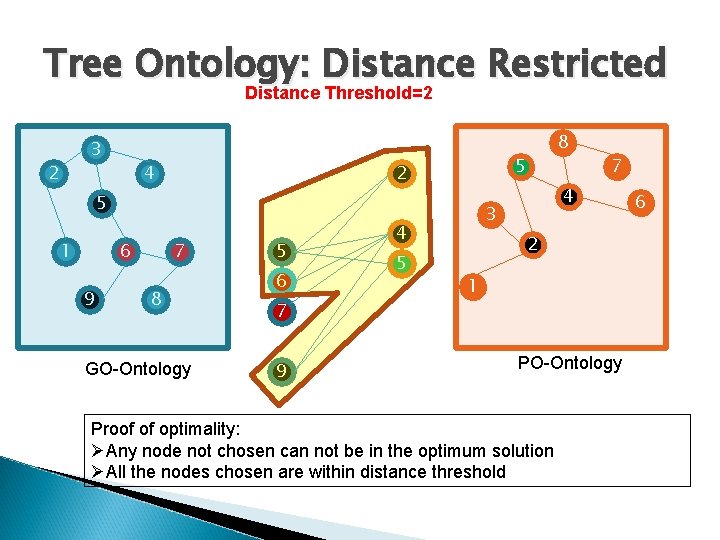
Tree Ontology: Distance Restricted Distance Threshold=2 3 2 4 5 2 5 1 6 9 7 8 GO-Ontology 5 6 7 9 7 4 3 4 5 8 2 1 PO-Ontology Proof of optimality: ØAny node not chosen can not be in the optimum solution ØAll the nodes chosen are within distance threshold 6

Distance Restricted Dense Subgraph Guess a small subset of nodes from the optimum Choose candidate nodes by considering distance from the guessed nodes Compute the densest subgraph by restricting the gene annotation graph to only the chosen nodes

Subset Restricted Dense Subgraph Are all dense subgraphs biologically meaningful ? ◦ How do we some control over the kind of dense subgraphs that are found ? Restrictions in dense subgraph computation Distance Restricted Subset Restricted Given a subset of GO, PO terms compute the densest subgraph containing them.

Subset Restricted Dense Subgraph 1 2 2 2 3 4 1 1 5 1 1 7 • This set {5, 6} must be in the solution. 6 1 1 1 8 • Density of {1, 2, 3, 4} = (3+2+2+2)/4 = 2. 25– Doesn’t contain {5, 6} • Density of {5, 6, 7, 8} = 6/4 = 1. 5 (Satisfies subset requirement) • Density of {1, 2, 3, 4, 5, 6, 7, 8} = (2+3+2+2+1*7)/8 = 2. 0 (Best answer) Polynomial time algorithm to compute the optimum solution

Specified Set of Nodes in Densest Subgraph For this problem we modified Lawler’s method of finding densest subgraphs. Let’s assume that we have a graph in which we want to force {5, 6} to be in the final solution.

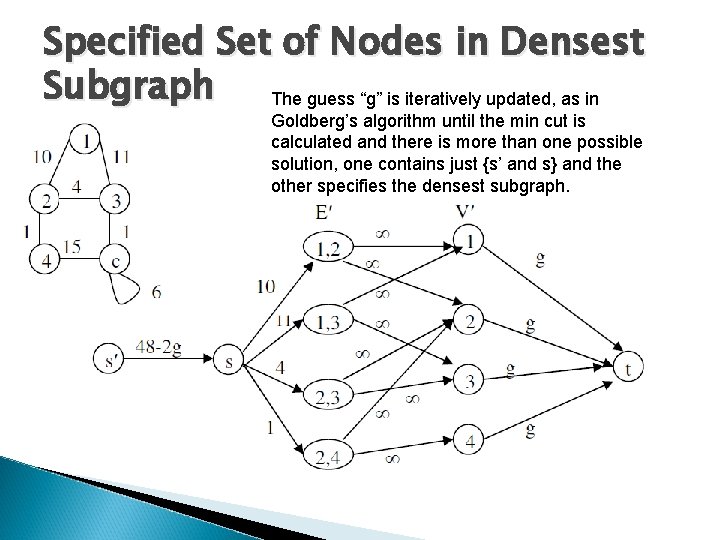
Specified Set of Nodes in Densest Subgraph The guess “g” is iteratively updated, as in Goldberg’s algorithm until the min cut is calculated and there is more than one possible solution, one contains just {s’ and s} and the other specifies the densest subgraph.

All Almost Dense Subgraph A graph may contain multiple subgraphs of equal (or close to equal) density Computing just one subgraph may not be sufficient Compute all subgraphs close to maximum density Extension of Picard and Queyranne’s result ◦ Polynomial time algorithm to find almost all dense subgraphs given the number of such subgraphs is polynomial in the number of vertices. ◦ Their method encodes all possible s-t min cuts. ◦ After a max-flow is found, we lower edges with residual capacity close to zero, to zero and now used [PQ] method to list all s-t min cuts. Can be extended to consider both distance and subset restriction

All Almost Dense Subgraphs 1 2 2 2 3 2 4 3 • Density of {1, 2, 3, 4} = 9/8 = 2. 25 1 1 6 1 7 1 2 9 8 2 2 • Density of {5, 6, 7, 8, 9} = 11/5 = 2. • Density of {1, 2, 3, 4, 5, 6, 7, 8, 9} = 21/9 = 2. 333 • The entire graph is the densest subgraph, but {1, 2, 3, 4} and {5, 6, 7, 8, 9} are “almost” dense subgraphs

Photomorphogenesis Experiment Ø 10 Photomorphogenesis genes ØCIB 5 CRY 2 HFR 1 COP 1 PHOT 2 HY 5 SHB 1 CRY 1 CIB 1 Ø 66 GO CV terms. 41 PO CV terms; 2230 GO-PO edges. ØGenerate distance restricted dense subgraph. q GO distance = 2. q PO distance = 3. q Dense subgraph with 3 GO terms & 13 PO terms

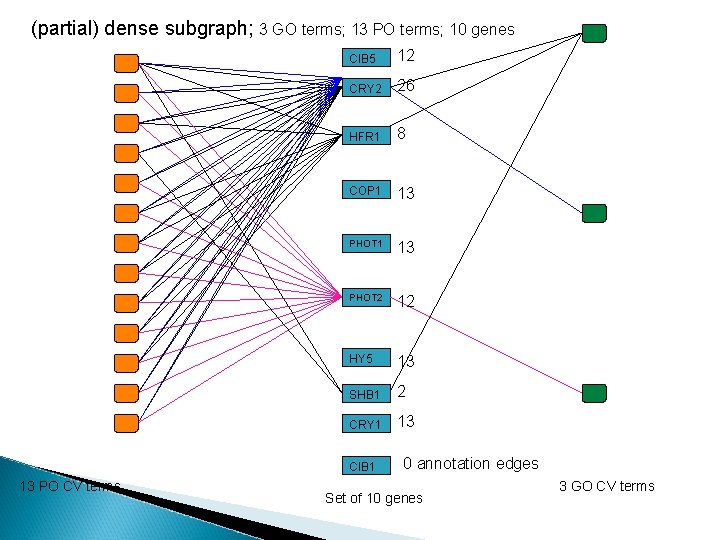
(partial) dense subgraph; 3 GO terms; 13 PO terms; 10 genes CIB 5 12 CRY 2 26 HFR 1 8 COP 1 13 PHOT 2 12 HY 5 13 SHB 1 2 CRY 1 13 CIB 1 13 PO CV terms 0 annotation edges Set of 10 genes 3 GO CV terms

Potential Discovery Ø Genes CRY 2 and PHOT 1 are both observed in the dense subgraph with the following two GO and PO combinations: 5773: vacuole: cellular_component 13: cauline leaf; plant_structure 37: shoot apex; plant_structure (5773, 13) (5773, 37) Ø This pattern has not been reported in the literature. Two independent studies [Kang et al. Planta 08, Ohgishi PNAS 04] have suggested that there may be some functional interactions between the members of PHOT 1 and CRY 2 in vacuole

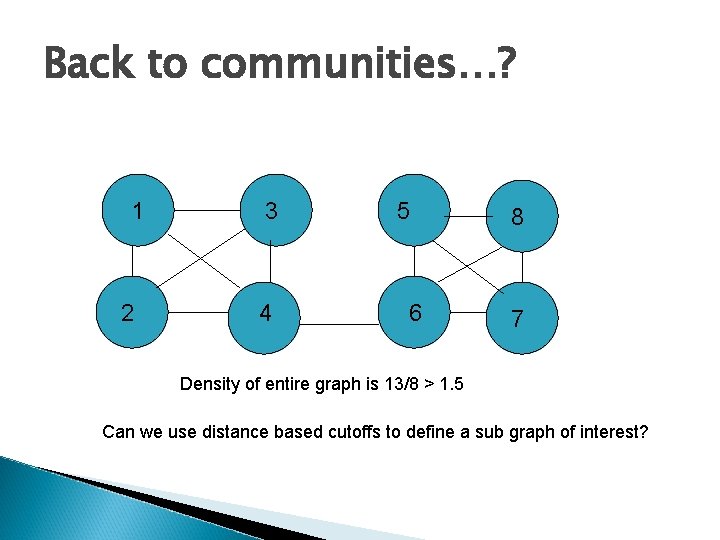
Back to communities…? 1 2 3 4 5 6 8 7 Density of entire graph is 13/8 > 1. 5 Can we use distance based cutoffs to define a sub graph of interest?

Conclusion & Future Works. . Identifying dense subgraphs with distance and subset restriction may help in identifying interesting patterns Potential Applications in other domains: ◦ Distance restricted dense subgraph for community detection ◦ Subset restricted dense subgraph in PPI network for deriving protein complexes Ranking almost dense subgraphs Change the notion of density [K, Mukherjee, Saha]?