Dendroscope An interactive viewer for large phylogenetic trees

Dendroscope – An interactive viewer for large phylogenetic trees - and networks Daniel H. Huson 1 Phylogenetics Programme, Newton Institute, September 2007

Overview l Dendroscope and large trees l Phylogenetic networks – cluster networks l Dendroscope 2 and phylogenetic networks 2

Yet Another Tree Viewer? l l http: //evolution. genetics. washington. edu /phylip/software. html: Yet… no existing program “does it all” 3

Requirements l l l Provide all standard visualizations Allow interactive setting of line widths, colors and fonts Allow rerooting , reordering, hiding, deletion and subtree extraction Open and save in different formats, including standard graphics formats Run on large files with many trees or large trees (with a million nodes) Run on all major operating systems 4

Eight Different Views 5

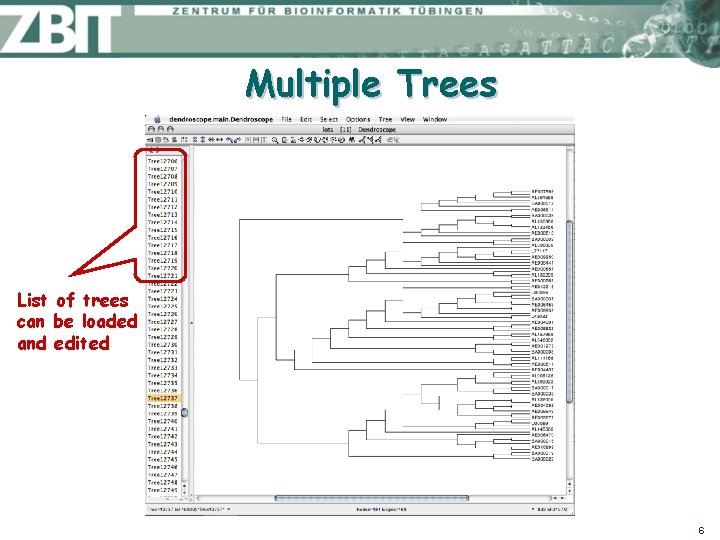
Multiple Trees List of trees can be loaded and edited 6

Large Trees NCBI taxonomy ~325, 000 taxa 7

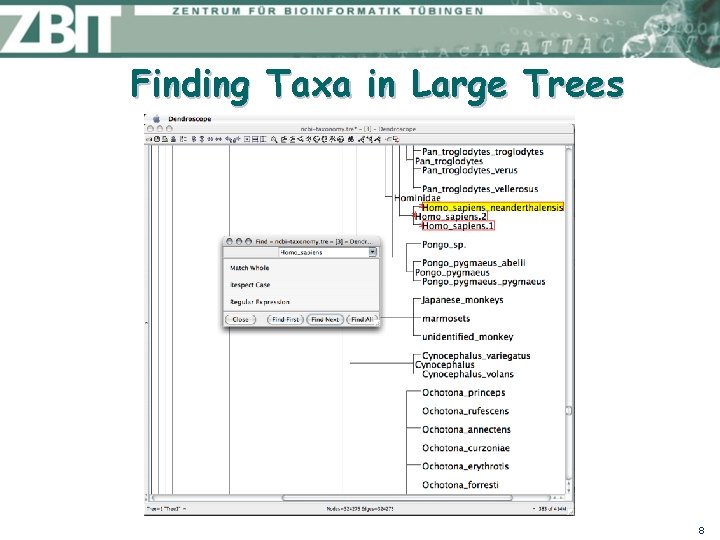
Finding Taxa in Large Trees 8

Subtree Extraction Select a set of taxa and extract the induced subtree 9

Overview l Dendroscope and large trees l Phylogenetic networks – cluster networks l Dendroscope 2 and phylogenetic networks 10

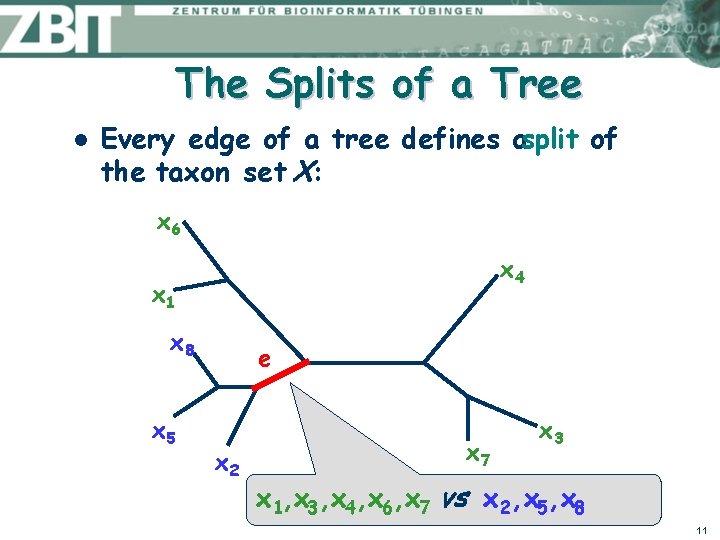
The Splits of a Tree l Every edge of a tree defines asplit of the taxon set X: x 6 x 4 x 1 x 8 x 5 e x 2 x 7 x 3 x 1, x 3, x 4, x 6, x 7 vs x 2, x 5, x 8 11

Trees and Compatible Splits The set of all splits obtained from T is called the split encoding (T) of T l Theorem An arbitrary set of splits is the split encoding of some unique tree T, if and only if any two splits in are compatible. l How to represent incompatible splits? 12

Split Networks l Display incompatible splits bands of parallel edges using B ( andelt & Dress, 1992) l l l Boxes artifacts of this, nonintuitive for users? Size of network can be exponential in # of splits Only drawn in unrooted radial layout Different from reticulate networks Find a new way to represent incompatible splits? 13

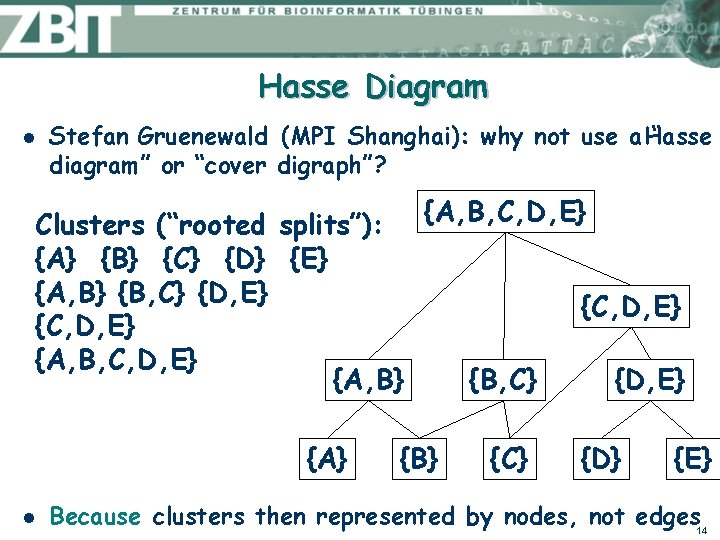
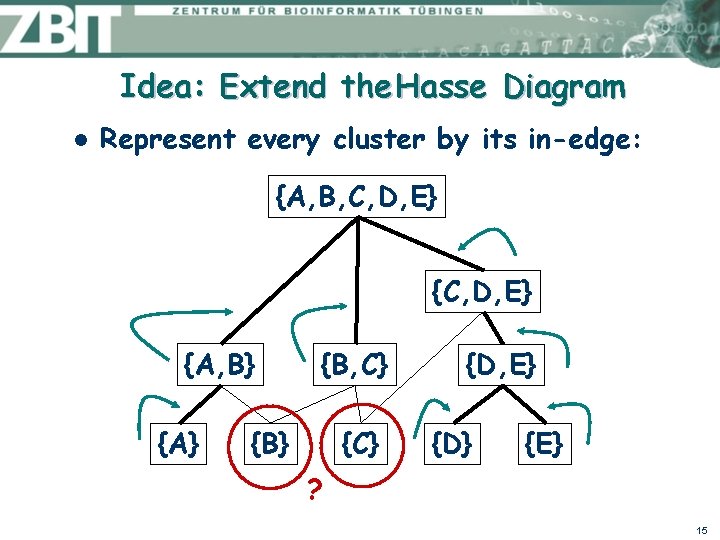
Hasse Diagram l Stefan Gruenewald (MPI Shanghai): why not use a Hasse “ diagram” or “cover digraph”? Clusters (“rooted splits”): {A, B, C, D, E} {A} {B} {C} {D} {E} {A, B} {B, C} {D, E} {C, D, E} {A, B, C, D, E} {A, B} {B, C} {D, E} {A} l {B} {C} {D} {E} Because clusters then represented by nodes, not edges 14

Idea: Extend the Hasse Diagram l Represent every cluster by its in-edge: {A, B, C, D, E} {A, B} {A} {B, C} {B} {C} {D, E} {D} {E} ? 15

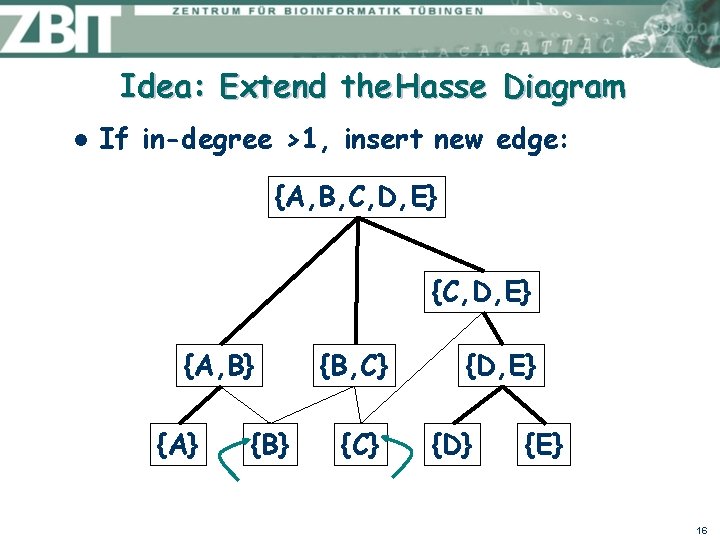
Idea: Extend the Hasse Diagram l If in-degree >1, insert new edge: {A, B, C, D, E} {A, B} {A} {B, C} {D, E} {D} {E} 16

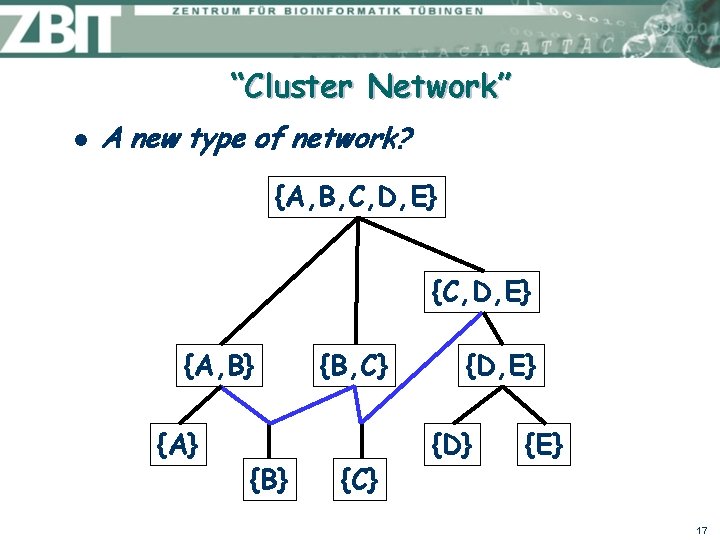
“Cluster Network” l A new type of network? {A, B, C, D, E} {A, B} {A} {B, C} {D, E} {D} {E} 17

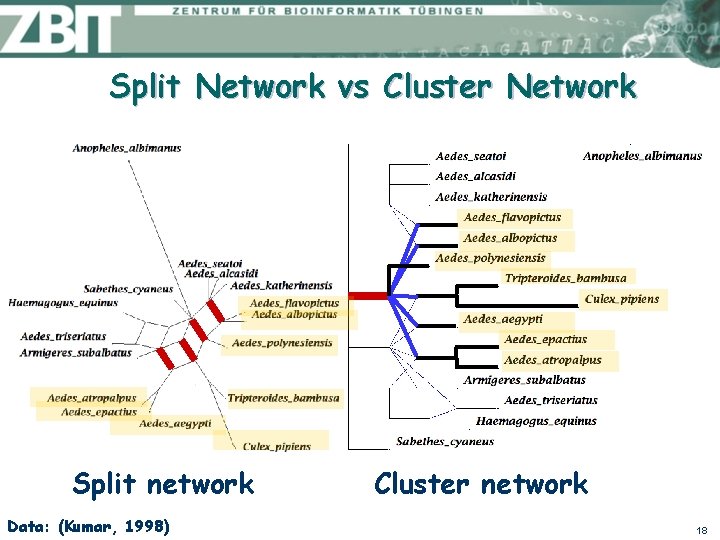
Split Network vs Cluster Network Split network Data: (Kumar, 1998) Cluster network 18

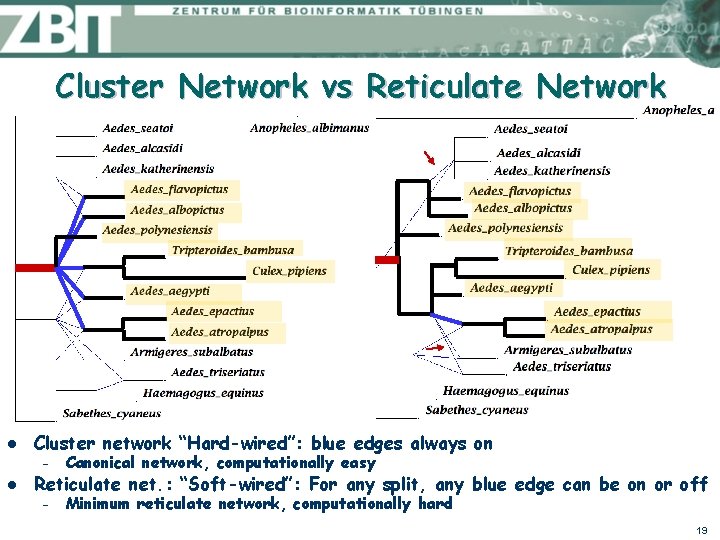
Cluster Network vs Reticulate Network l l Cluster network “Hard-wired”: blue edges always on – Canonical network, computationally easy – Minimum reticulate network, computationally hard Reticulate net. : “Soft-wired”: For any split, any blue edge can be on or off 19

Overview l Dendroscope and large trees l Phylogenetic networks – cluster networks l Dendroscope 2 and phylogenetic networks 20

Dendroscope 2 l l Computation of different consensus trees and super trees Computation of different consensus networks and super networks Use “extended Newick” format to support cluster networks and reticulate networks All features of Dendroscope 1 will also apply to networks 21

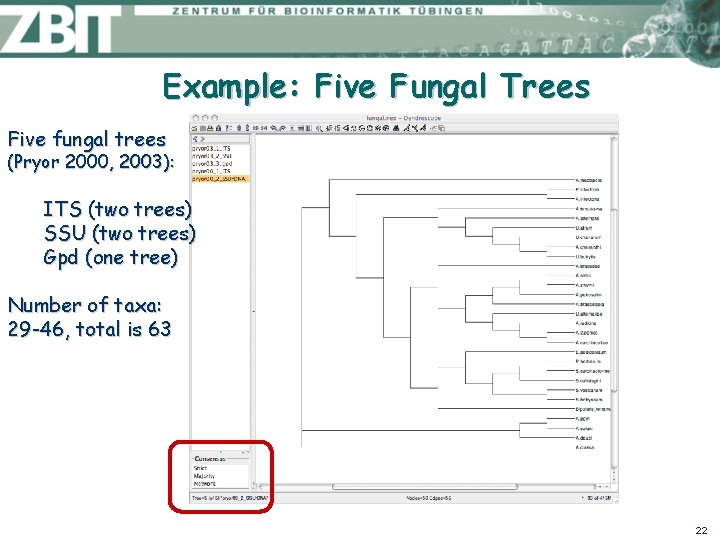
Example: Five Fungal Trees Five fungal trees (Pryor 2000, 2003): ITS (two trees) SSU (two trees) Gpd (one tree) Number of taxa: 29 -46, total is 63 22

“Strict Consensus Tree” 23

“Majority Consensus Tree” 24

Consensus Super Network, >20% support 25

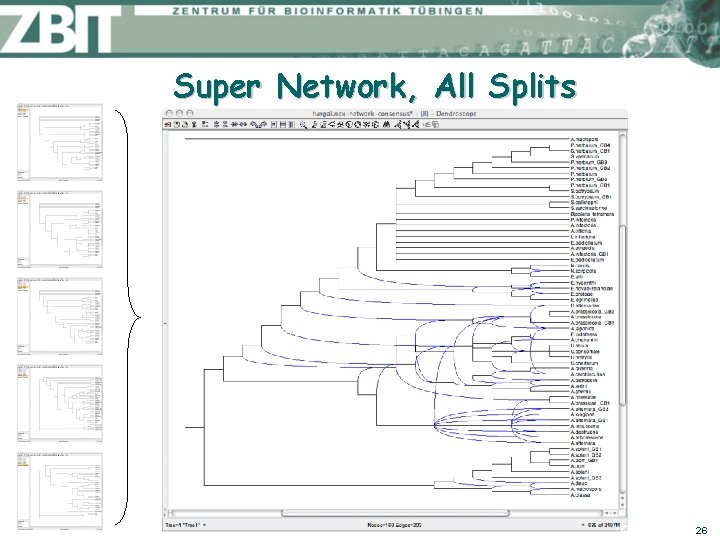
Super Network, All Splits 26

Summary l l Dendroscope 1: new interactive tool for visualizing & editing phylogenetic trees Cluster networks: new type of phylogenetic networks that are easy to compute and “look more like trees” Dendroscope 2: will contain consensus methods and will read, write and draw cluster- and reticulate networks. Dendroscope 1 is freely available from: www-ab. informatik. uni-tuebingen. de/software. dendroscope 27

Credits l Contributions to Dendroscope from: – l Super network algorithm (Z-closure) joint work with: – l Tobias Dezulian , Markus Franz, Christian Rausch, Daniel Richter & Regula Rupp Tobias Dezulian , Tobias Klöpper and Steel Mike Filtered super network joint work with: – Mike Steel and Jim Whitfield 28