Demonstrating how specific concrete examples of puzzles riddles











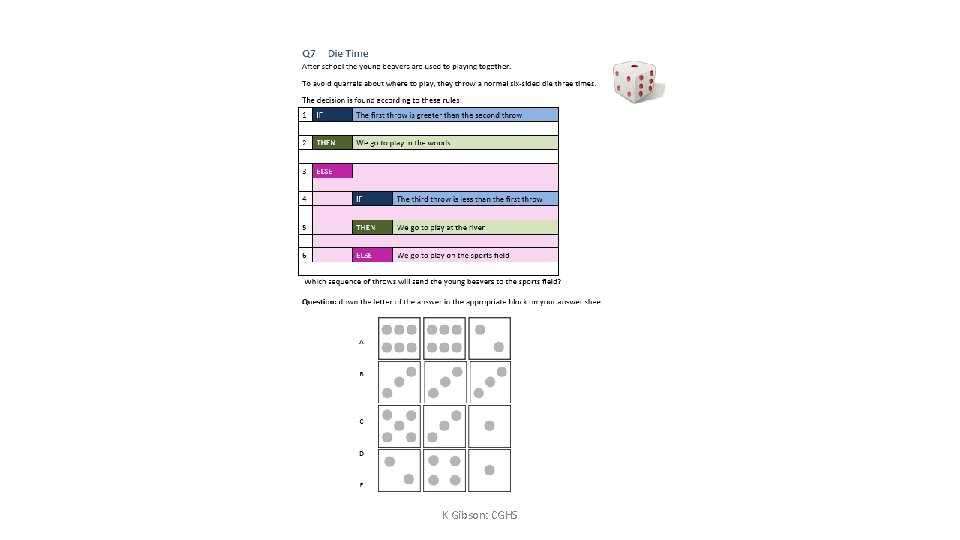


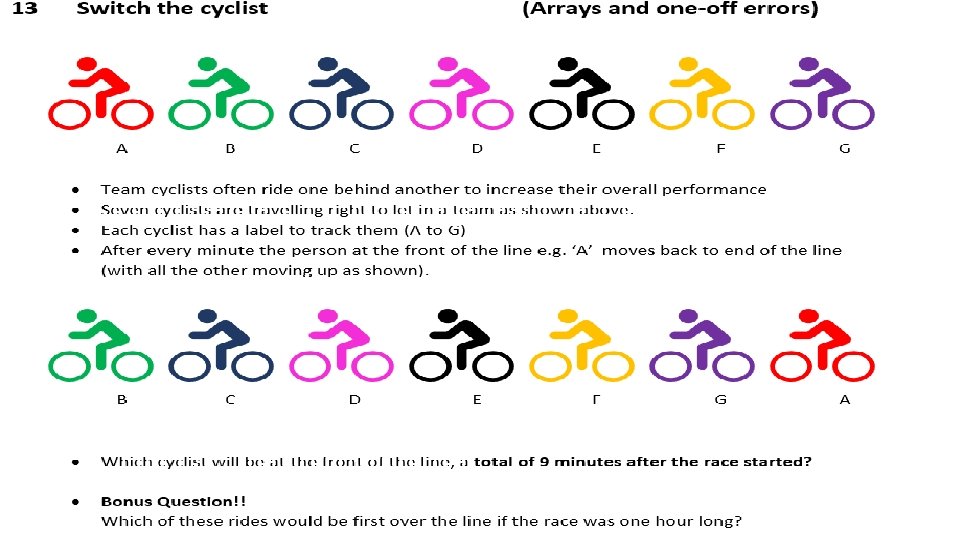




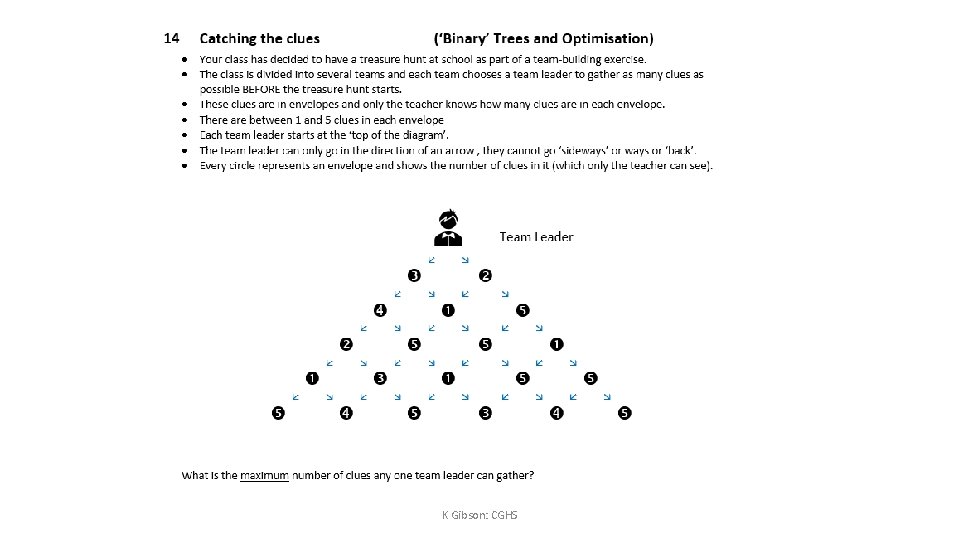
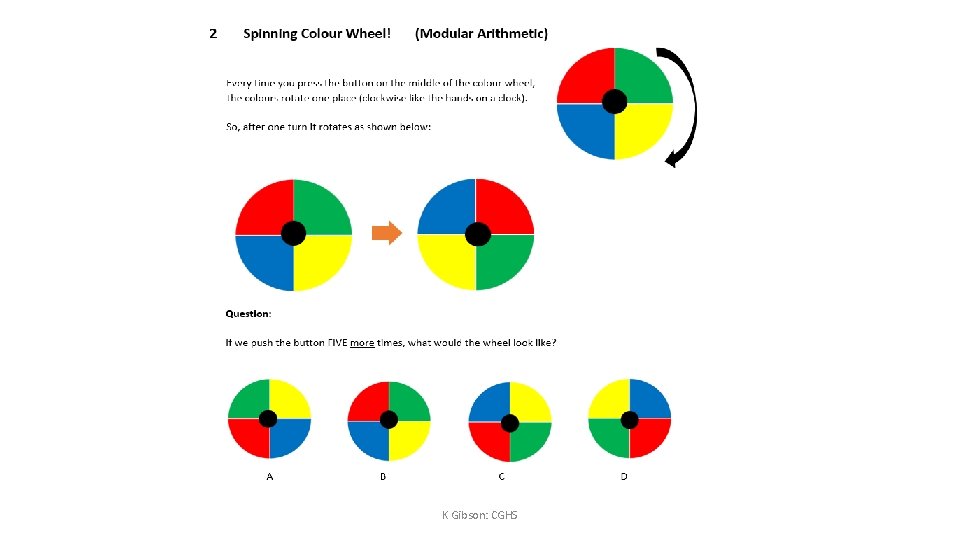


- Slides: 23

Demonstrating how specific concrete examples of puzzles, riddles and pattern recognition and problems can be used to introduce paper-based problem solving whilst having fun! Pupils should learn (without knowing) how to make use of computational thinking techniques without using any complicated technology or terminology. K Gibson: CGHS

Some background Excited Teacher • Been teaching for 35 years and have been involved in CAT and IT but also been a reluctant Maths, Science and LO Teacher! • Started at Collegiate Girls’ High in PE last year to start IT as a subject. • Started experimenting with grade 8 and 9 classes during Covid to experiment with problem solving without computers (all girls do have). • Premise was to have fun whilst ‘invisibly’ learning problem solving by looking at riddles and puzzles and ‘Talent Search’ type questions. • Started adapting questions to ‘bend them’ towards computational thinking skills without ever mentioning the complicated terminology. • In one year we doubled the IT numbers and have a created a huge buzz! • The adage was/is life is all about problem solving (and we don’t mean Maths K Gibson: CGHS

Principles Really excited teacher • Learn while having fun • Grade the problems so they are access to all • It about ‘growing’ real-life problem solving skills • What are the actual constraints, can I change something, can I partially solve? • Keep instructions simple / use graphics where possible • Be precise ‘when you need to’ with instructions • Contextualise within the learner’s realm • Its about the journey not just the product • The adage was/is life is all about problem solving (and we don’t mean Maths K Gibson: CGHS

Understanding problems and constraints • • • This is a ‘classic’ riddle I use first up (there are lots online) A farmer has to get a fox, a chicken, and a sack of mielies across a river. She has a boat, BUT it can only carry her and one other ‘thing’ in the boat If the fox and the chicken are ever left together, the fox will eat the chicken. If the chicken and the corn are ever left together, the chicken will eat the mielies, how does the farmer do it? • Discuss ‘out the box, wild’ solutions like ‘can the fox swim across? ’ • Learners can all get to the first step and be encouraged to work ‘graphically’, write down which ‘combinations work’ and which do not etc. K Gibson: CGHS

‘Codes’ Encryption and Decryption • Learners love ‘codes’ • Start simple with a basic ‘Shift’ algorithm where the letter A becomes B, the letter B becomes C etc , so ‘HOPE’ becomes ‘IPQF’ • Help/get the learners to write down the steps to follow (the algorithm, remembering and how to deal with the letter ‘Z’ and more complex ones where we ‘shift ‘by say 3 letters • An ‘agorithm’ With each letter in the word to be encoded, do the following • , , , , , , , , , , , , • • Brainstorm how to reverse this process (decryption). K Gibson: CGHS

Swopping order/values (Sequential Programming) • A crane responds to six different input commands: Left , Right , Up , Down , Grab , Release • Which is the correct set of instructions to swop the position of the two crates? A. (Down, Grab, Up, Right, Down, Release, Up) B. (Down, Grab, Up, Right, Down, Release, Up) (Right, Down, Grab, Up, Left, Down, Release, Up) (Right, Down, Grab, Up, Right, Down, Release) C. (Right, Down, Grab, Up) (Left, Down, Release, Up) D. (Down, Grab, Up, Right, Down, Release, Up) (Down, Grab, Left, Down, Release, Up) (Down, Grab, Up, Right, Down, Release, Up) E. None of the above are correct K Gibson: CGHS

Recognising solutions that match constraints • A farmer wants to sub-divide a square piece of land into 16 equal size plots give them to local NGOs. • His only restrictions are that: • no NGO may own more than THREE pieces of the land (the colours are the plots) • no NGO may own any land that is adjacent in any way to any other land they have i. e. they can never move from one piece of their land to another without going through someone else’s land first • Four proposals (colour-coded according to NGO) have been put forward – which, IF any, are acceptable ? K Gibson: CGHS

Patter recognition and optimisation: Chess Board • Need to colour ina produce a chess board using a robot that can • MR (move RIGHT ONE block), ML (move LEFT ONE block) MD (move DOWN ONE block) • PR (Paint current clock in RED) and PB (Paint current clock in BLACK) • RP n [instructions] • Initial steps/assumptions – make sure robot is IN correct starting position? • After the initial ‘brute force’ instructions or each line , try to identify patterns e. g. every second row etc. • introduce a new robot command - REPEAT n [instructions] which repeats instructions in brackets ‘n’ times e. g. . REPEAT 4 [PR MR PB MR] OR REPEAT 8 [ML] K Gibson: CGHS

Optimisation (1) • Carla the chameleon travels on the grid as shown below. The colours on the grid are: Red, Yellow, Pink, Green, Blue and Red • She moves between adjacent cells either horizontally, vertically or diagonally in any direction. • In a cell, a Carla has the same colour as the colour of the cell. • What is the minimum or least number of different colours that Carla can change to (including the initial colour) when she is travelling traveling from the lower left of the grid to the upper right? K Gibson: CGHS

Deduction, reprocessing constraints, Truth Tables K Gibson: CGHS

• keithg@cghs. za • Sites • https: //olympiad. org. za/talent-search/past-papers/pen-and-paper/ • https: //www. cemc. uwaterloo. ca/ • https: //cemc. uwaterloo. ca/contests/past_contests. html • https: //www. bebras. org http: //www. studyopportunities. co. za/resources/Brochures/Digital-Technology-brosjure. pdf K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS

K Gibson: CGHS