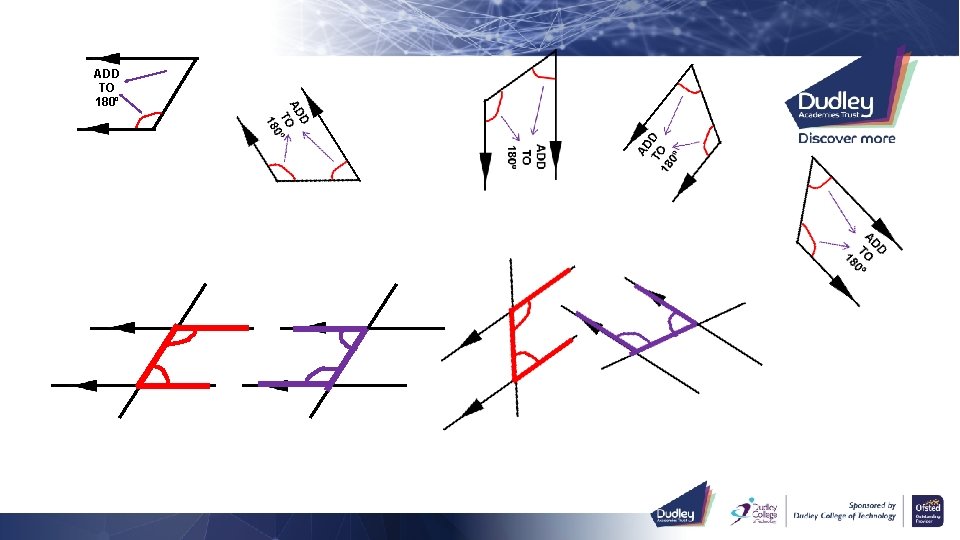
Demonstrate Find the size of the angles marked








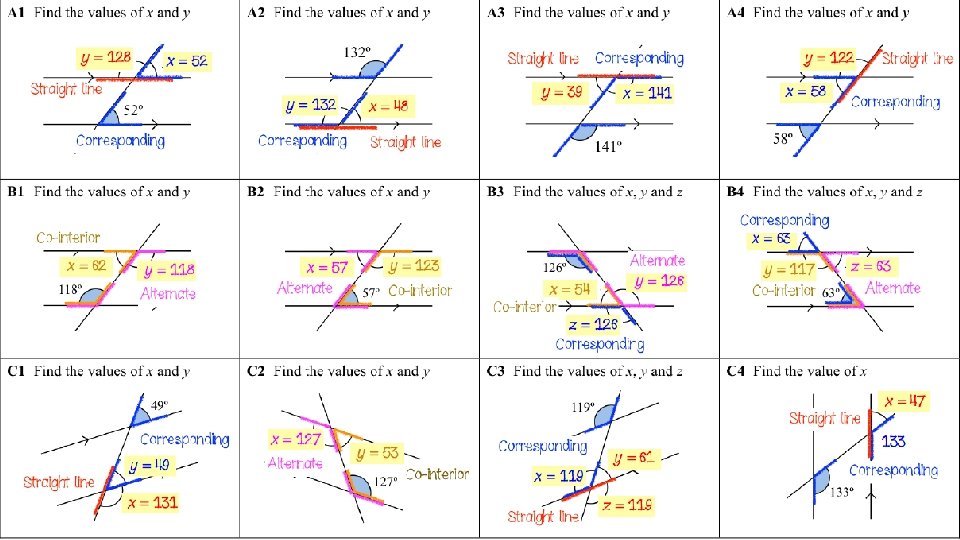






- Slides: 54

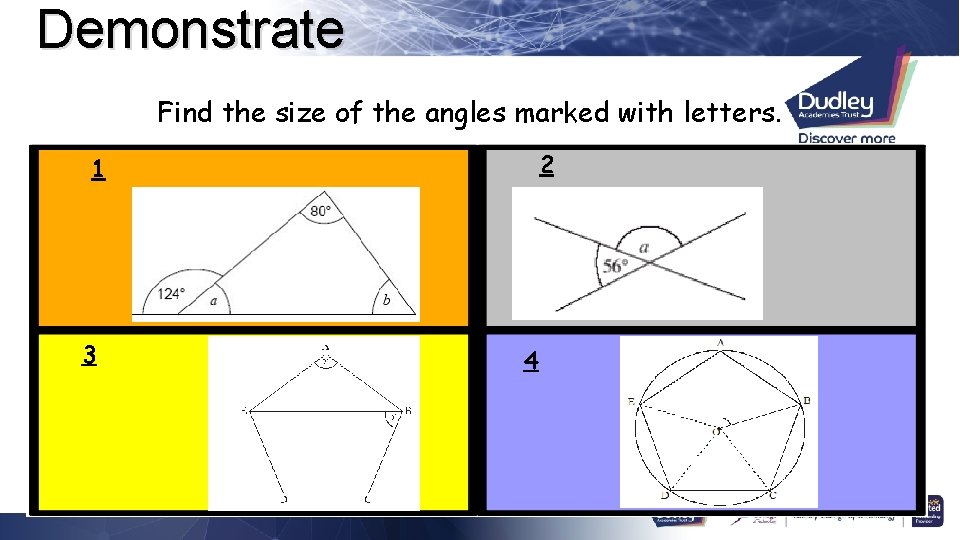
Demonstrate Find the size of the angles marked with letters. 2 1 3 4

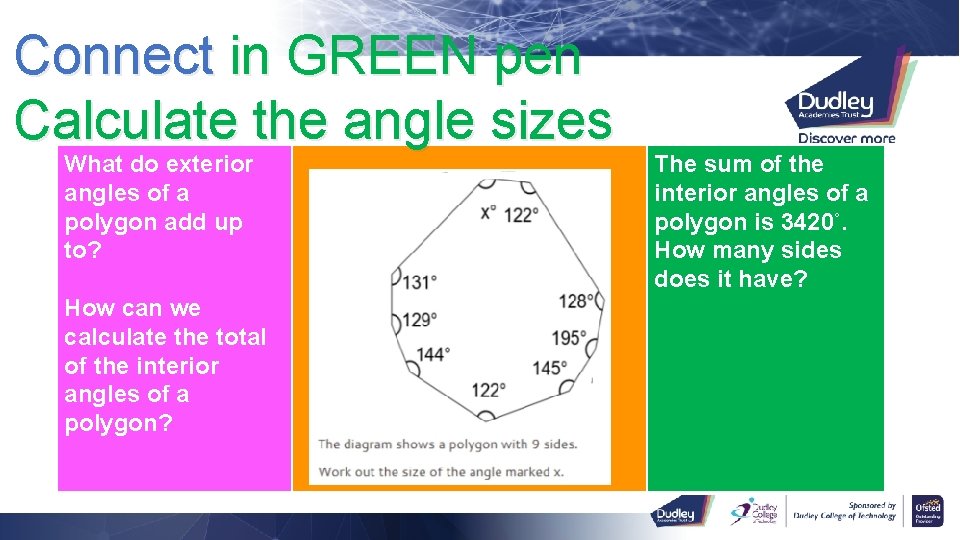
Connect in GREEN pen Calculate the angle sizes What do exterior angles of a polygon add up to? How can we calculate the total of the interior angles of a polygon? The sum of the interior angles of a polygon is 3420˚. How many sides does it have?

DNA Ask a question Make a statement

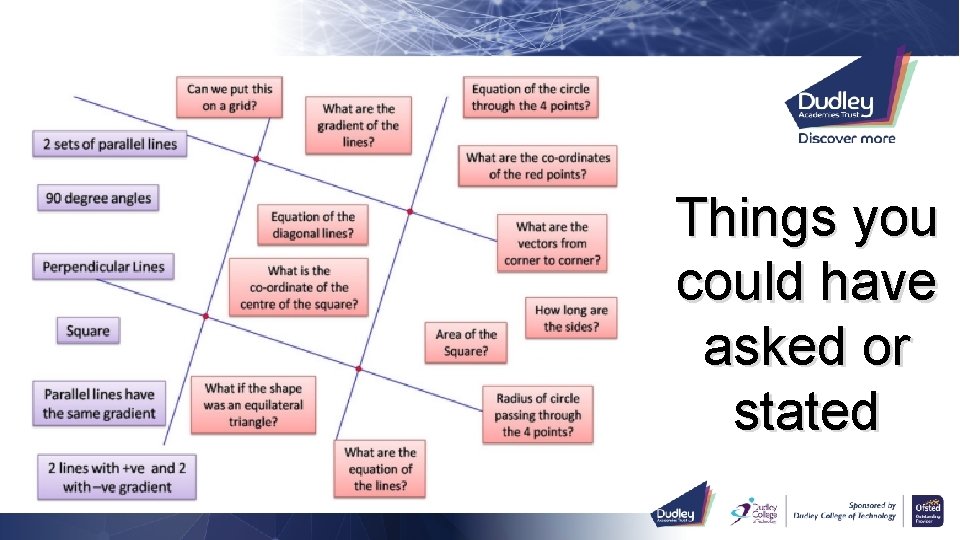
Things you could have asked or stated

Angles in parallel lines Unit 5 Objective d

Types of lines Parallel lines never meet We show they are parallel with two arrows

Types of lines Perpendicular lines meet at a right angle 90 o

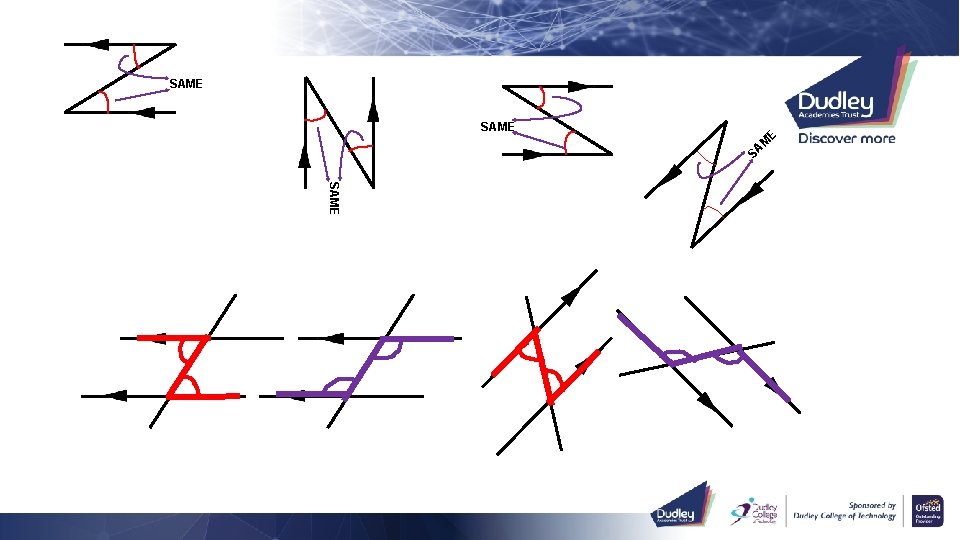
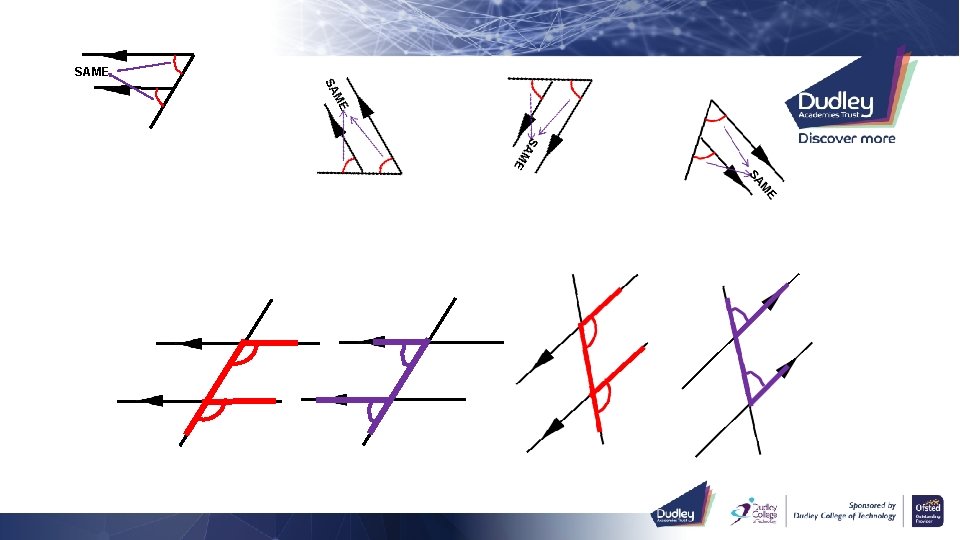
Angles in parallel lines investigation Work in pairs. Measure both angles in each diagram and write down your observations. Check that you have measured accurately!



SAME E M SA SAME


SAME


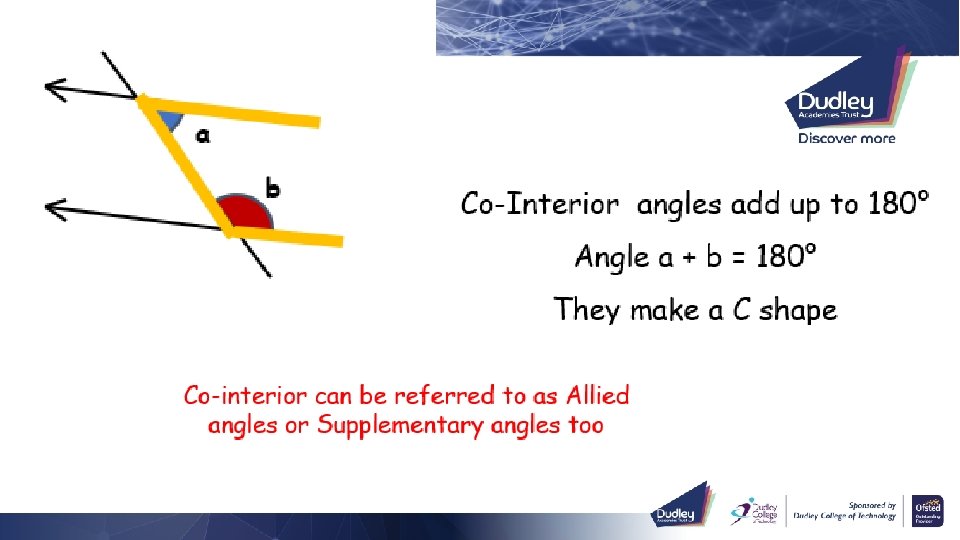
ADD TO 180º

Close your books Recall the information just learned

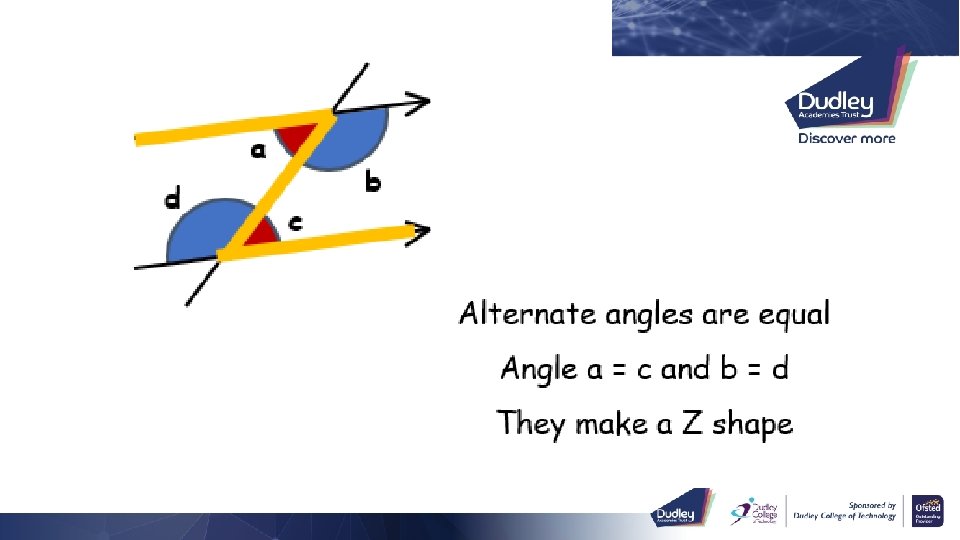
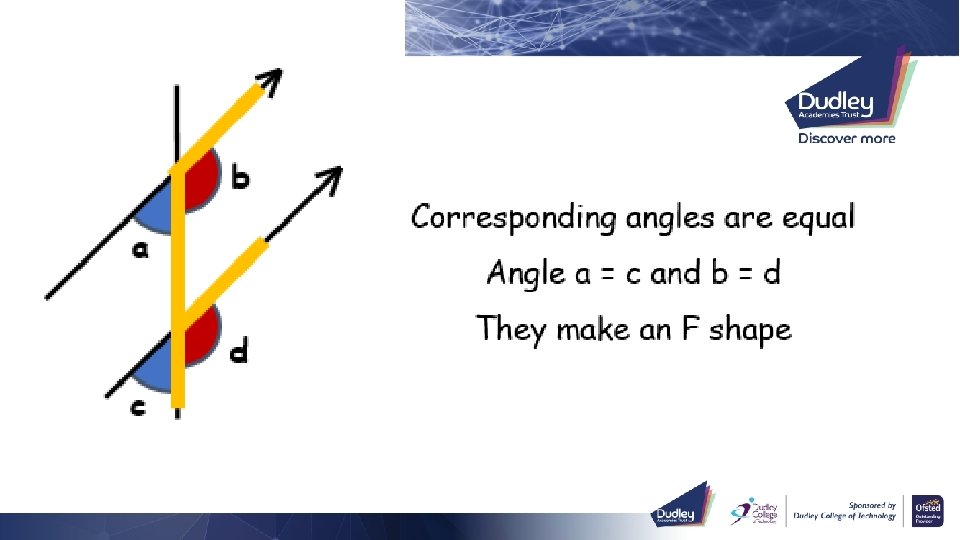
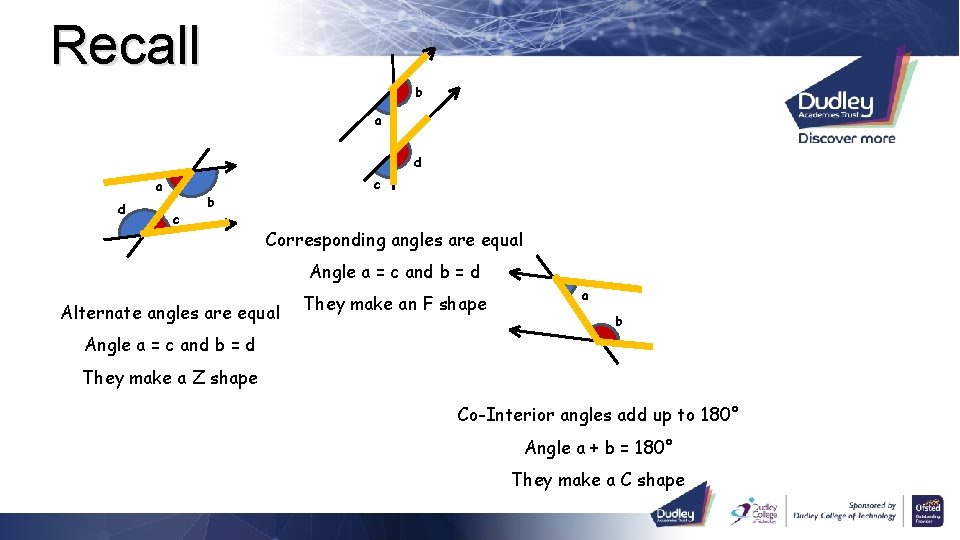
Recall b a d c c b Corresponding angles are equal Angle a = c and b = d Alternate angles are equal They make an F shape a b Angle a = c and b = d They make a Z shape Co-Interior angles add up to 180° Angle a + b = 180° They make a C shape

Hold up your planners to red, orange, green or blue pages on the count of three.

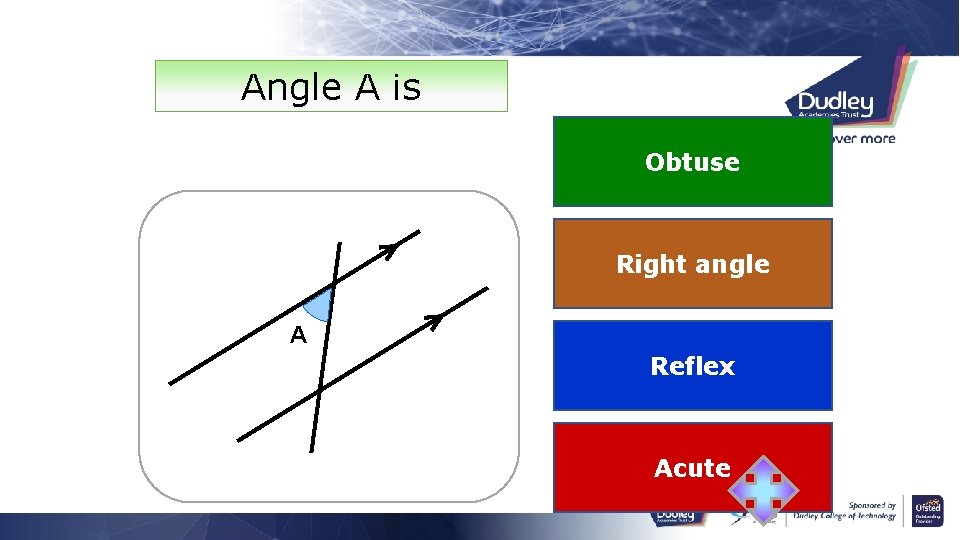
Angle A is Obtuse Right angle A Reflex Acute

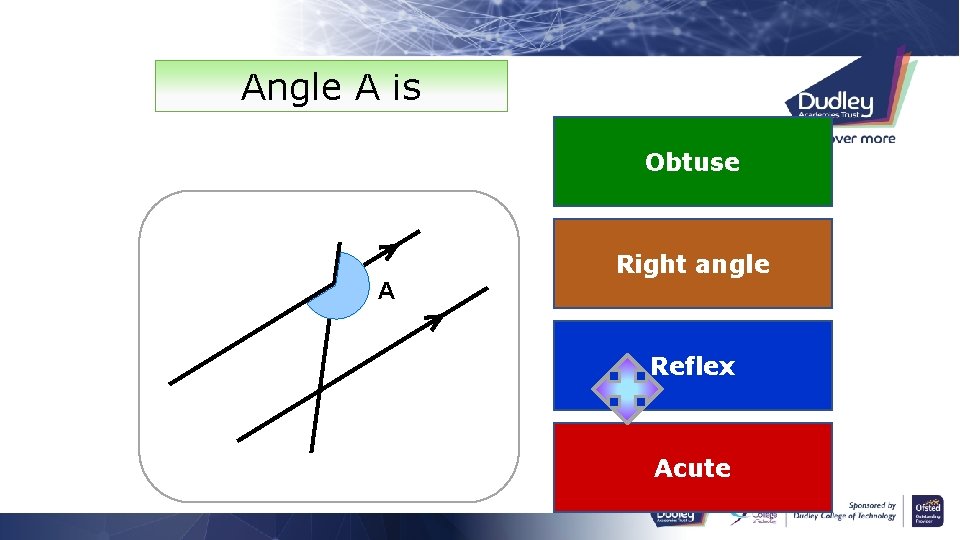
Angle A is Obtuse A Right angle Reflex Acute

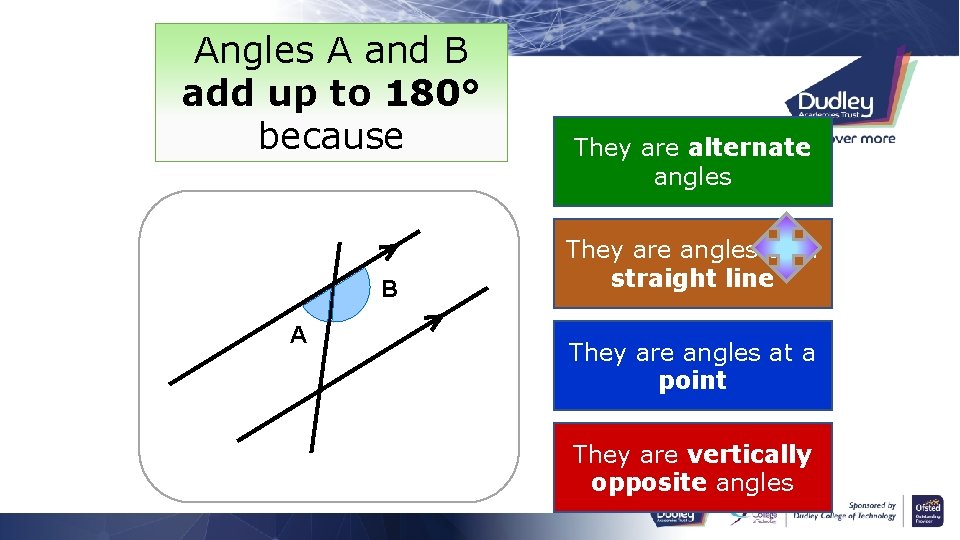
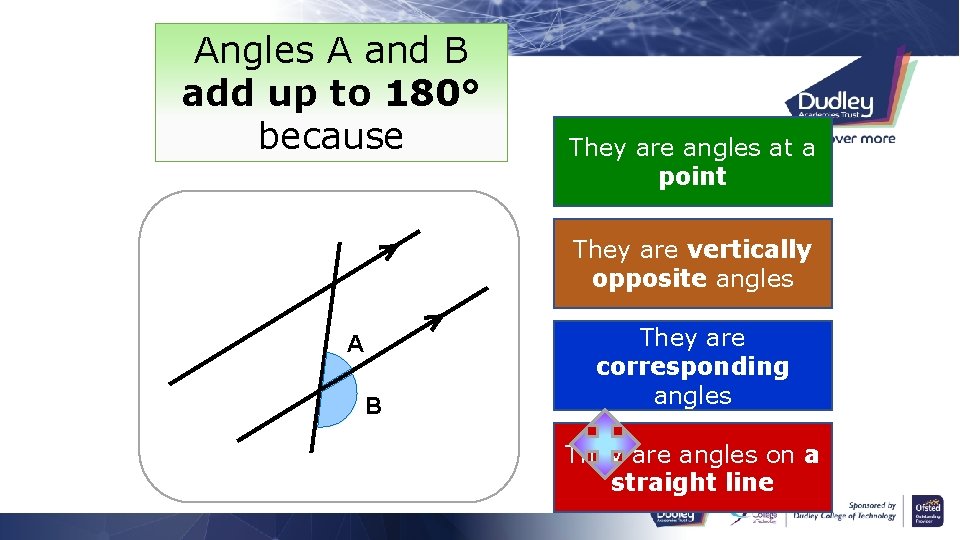
Angles A and B add up to 180° because B A They are alternate angles They are angles on a straight line They are angles at a point They are vertically opposite angles

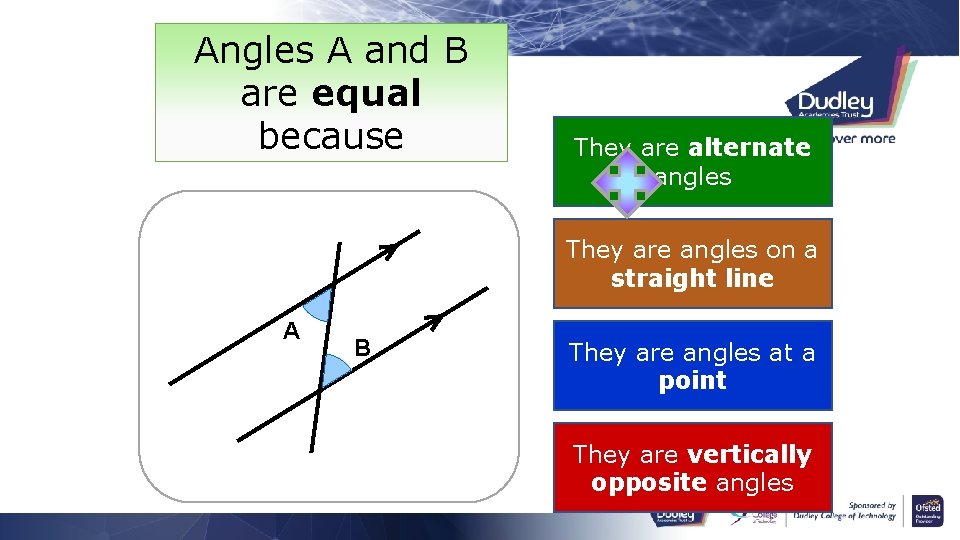
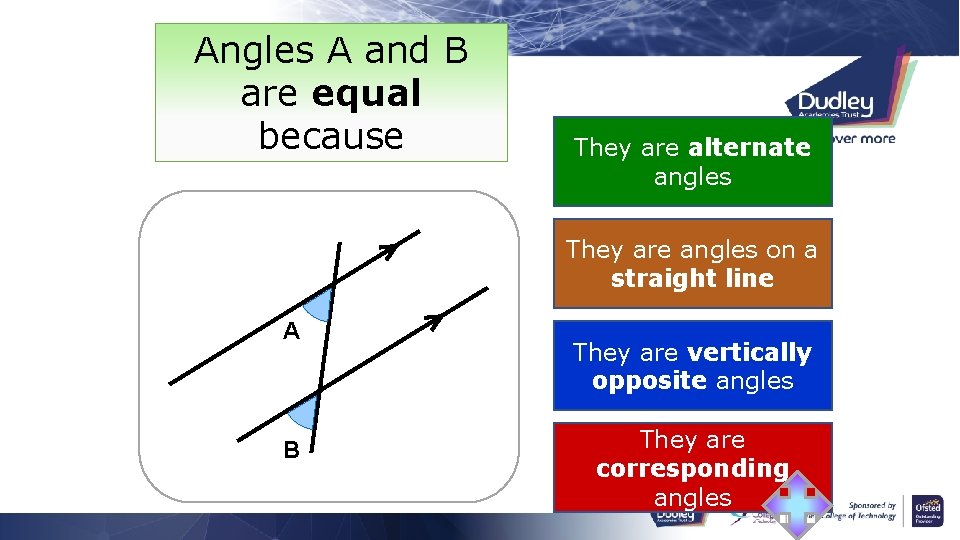
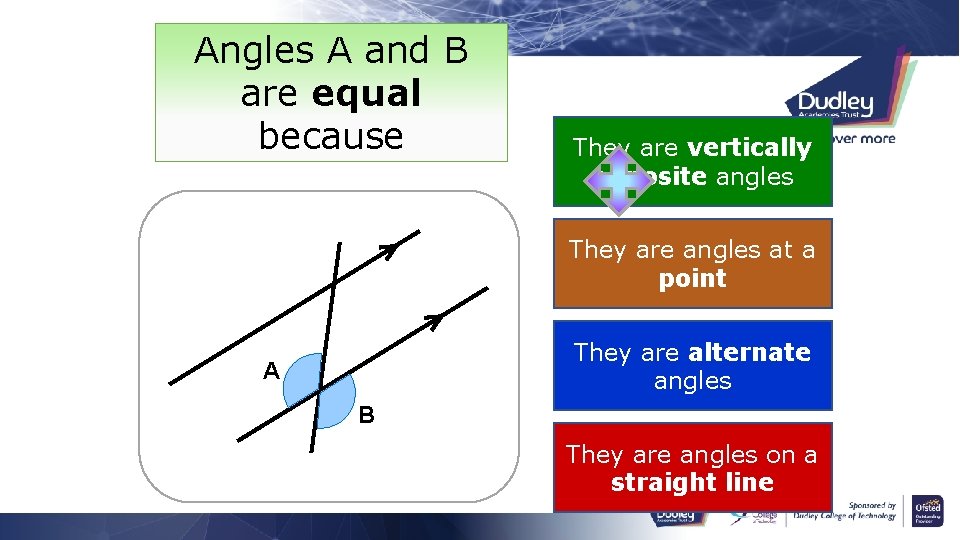
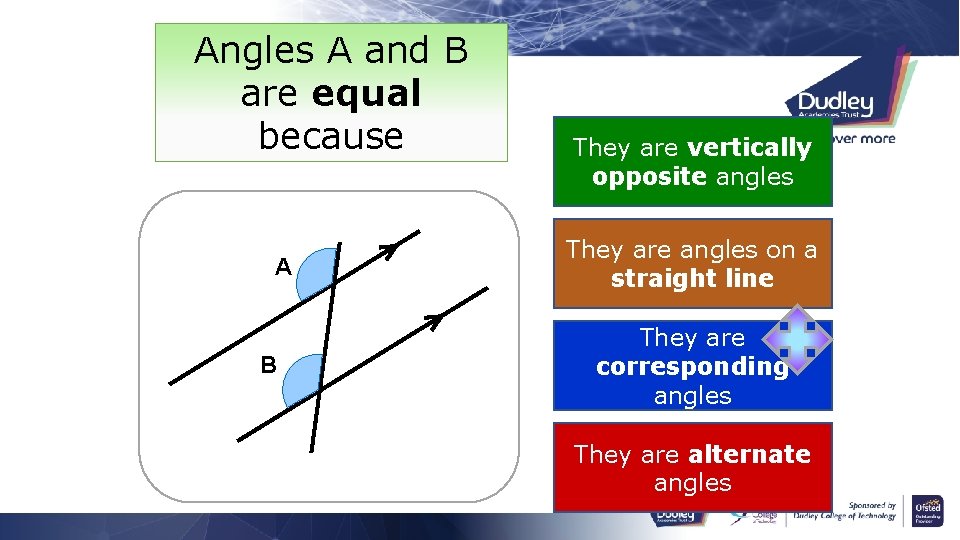
Angles A and B are equal because They are alternate angles They are angles on a straight line A B They are angles at a point They are vertically opposite angles

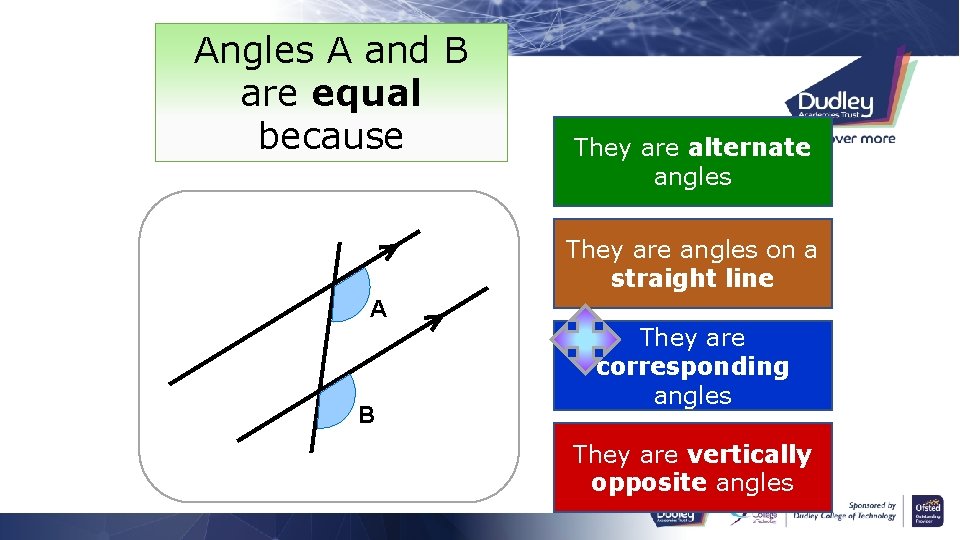
Angles A and B are equal because They are alternate angles They are angles on a straight line A B They are corresponding angles They are vertically opposite angles

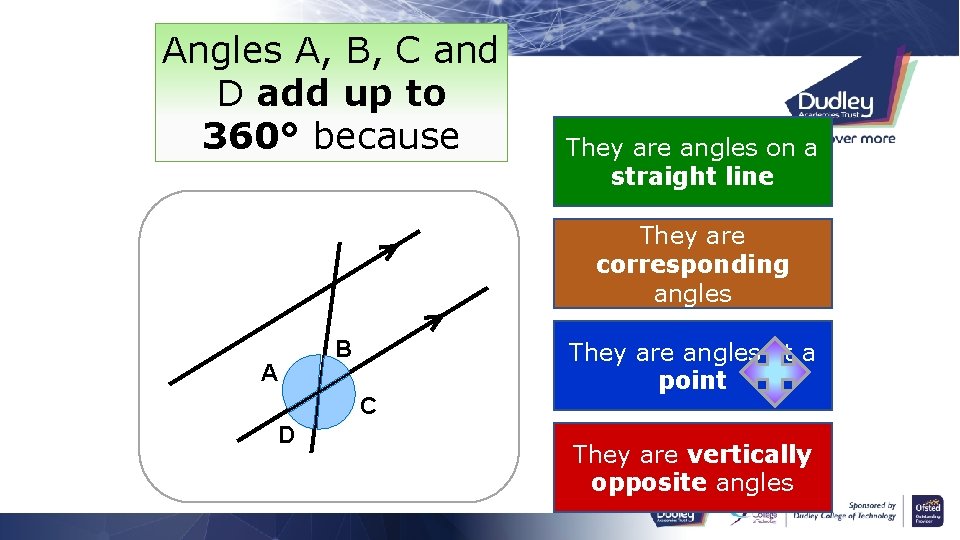
Angles A, B, C and D add up to 360° because They are angles on a straight line They are corresponding angles A B C D They are angles at a point They are vertically opposite angles

Angles A and B are equal because They are alternate angles They are angles on a straight line A B They are vertically opposite angles They are corresponding angles

Angles A and B are equal because They are vertically opposite angles They are angles at a point They are alternate angles A B They are angles on a straight line

Angles A and B are equal because A B They are vertically opposite angles They are angles on a straight line They are corresponding angles They are alternate angles

Angles A and B add up to 180° because They are angles at a point They are vertically opposite angles A B They are corresponding angles They are angles on a straight line

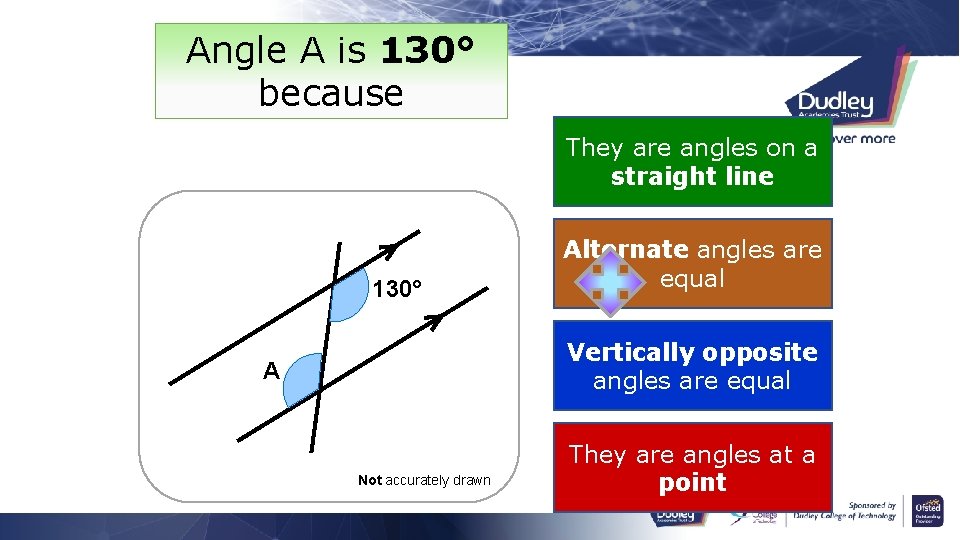
Angle A is 130° because They are angles on a straight line 130° Alternate angles are equal Vertically opposite angles are equal A Not accurately drawn They are angles at a point

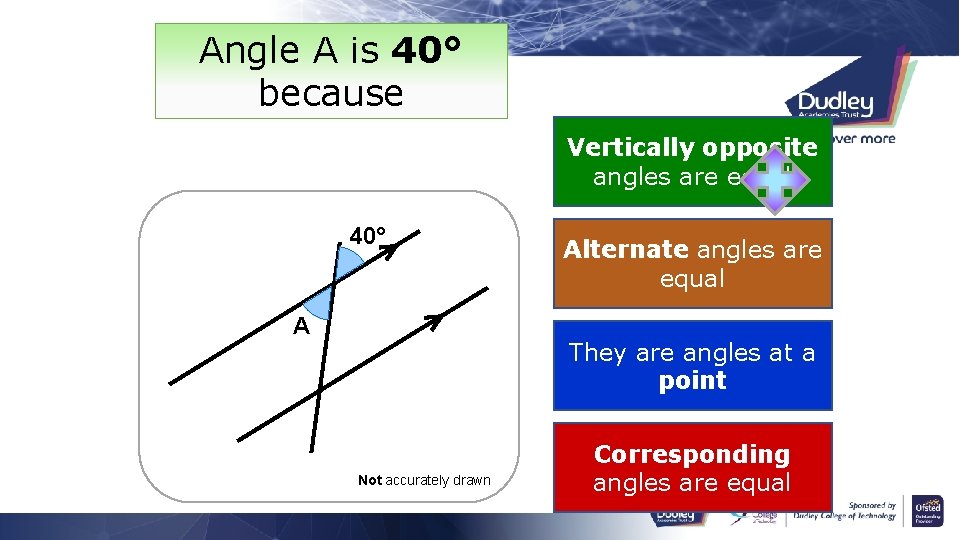
Angle A is 40° because Vertically opposite angles are equal 40° A Alternate angles are equal They are angles at a point Not accurately drawn Corresponding angles are equal

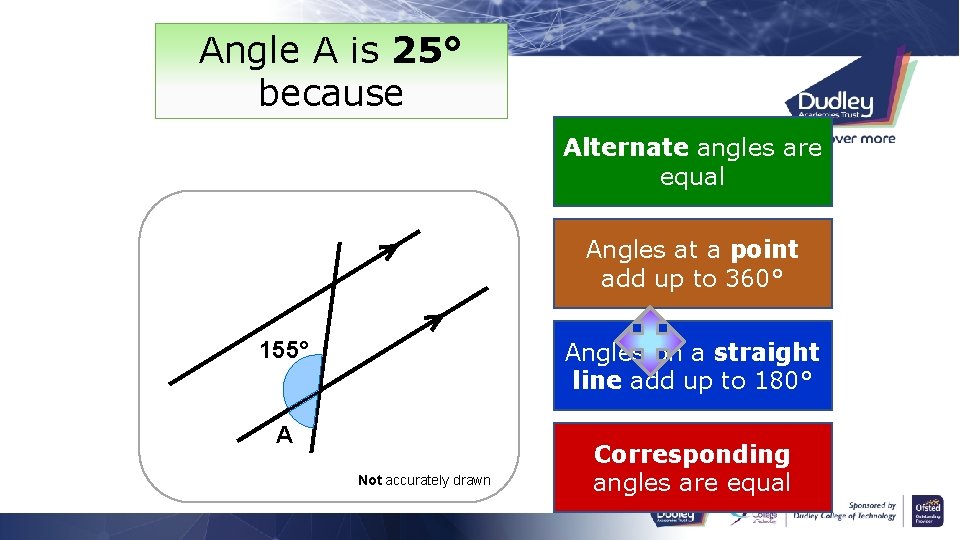
Angle A is 25° because Alternate angles are equal Angles at a point add up to 360° 155° Angles on a straight line add up to 180° A Not accurately drawn Corresponding angles are equal

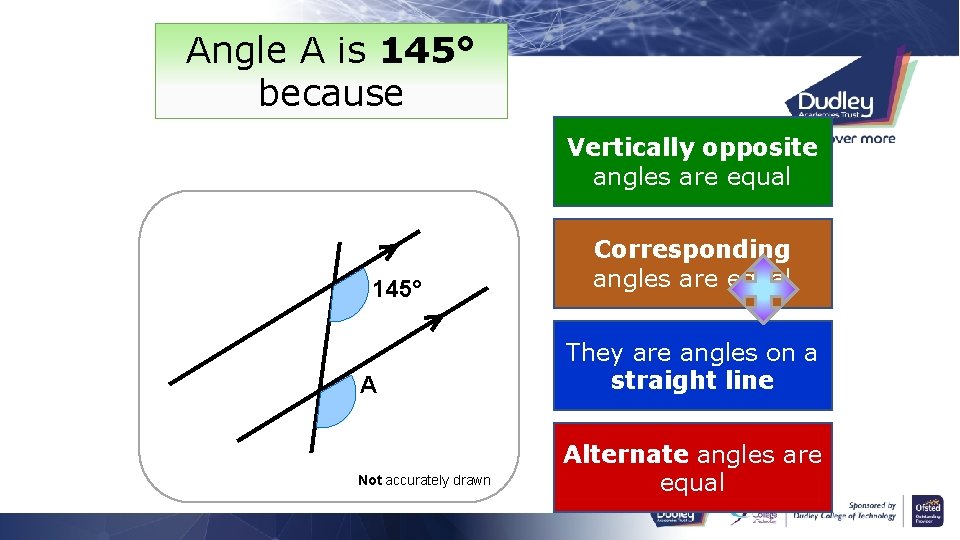
Angle A is 145° because Vertically opposite angles are equal 145° A Not accurately drawn Corresponding angles are equal They are angles on a straight line Alternate angles are equal

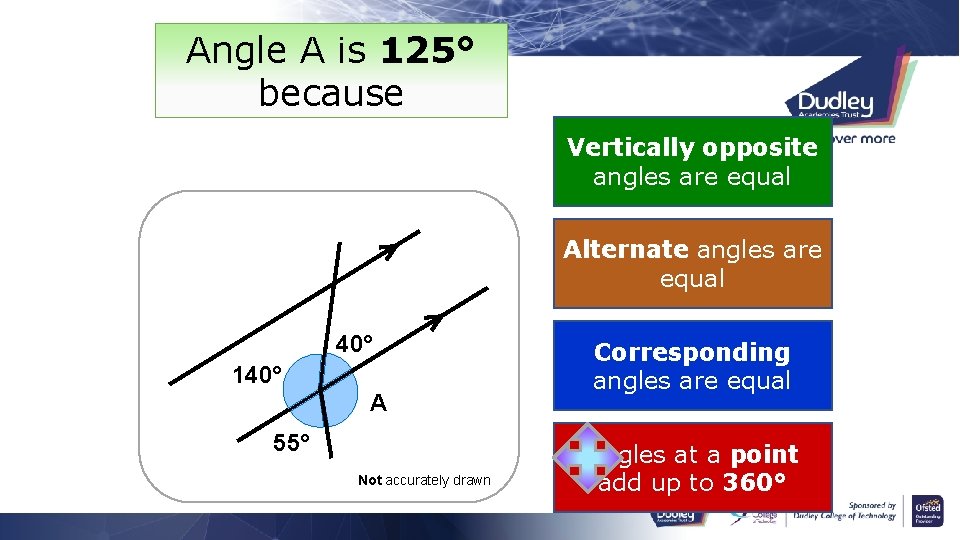
Angle A is 125° because Vertically opposite angles are equal Alternate angles are equal 40° 140° A 55° Not accurately drawn Corresponding angles are equal Angles at a point add up to 360°

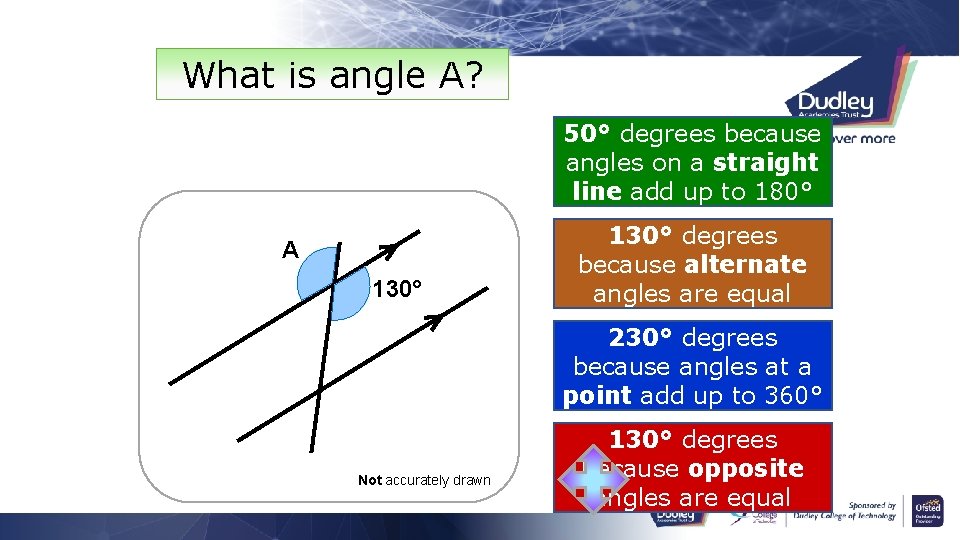
What is angle A? 50° degrees because angles on a straight line add up to 180° A 130° degrees because alternate angles are equal 230° degrees because angles at a point add up to 360° Not accurately drawn 130° degrees because opposite angles are equal

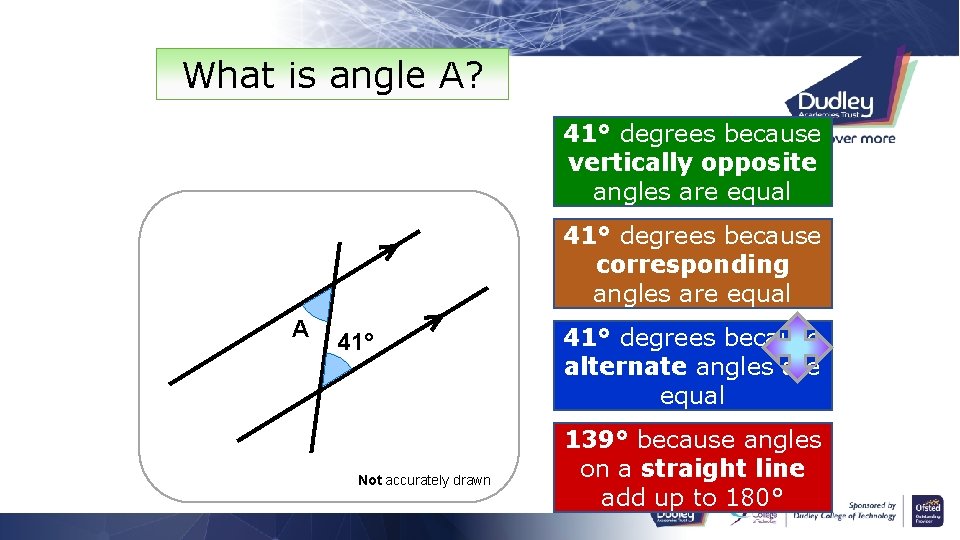
What is angle A? 41° degrees because vertically opposite angles are equal 41° degrees because corresponding angles are equal A 41° Not accurately drawn 41° degrees because alternate angles are equal 139° because angles on a straight line add up to 180°

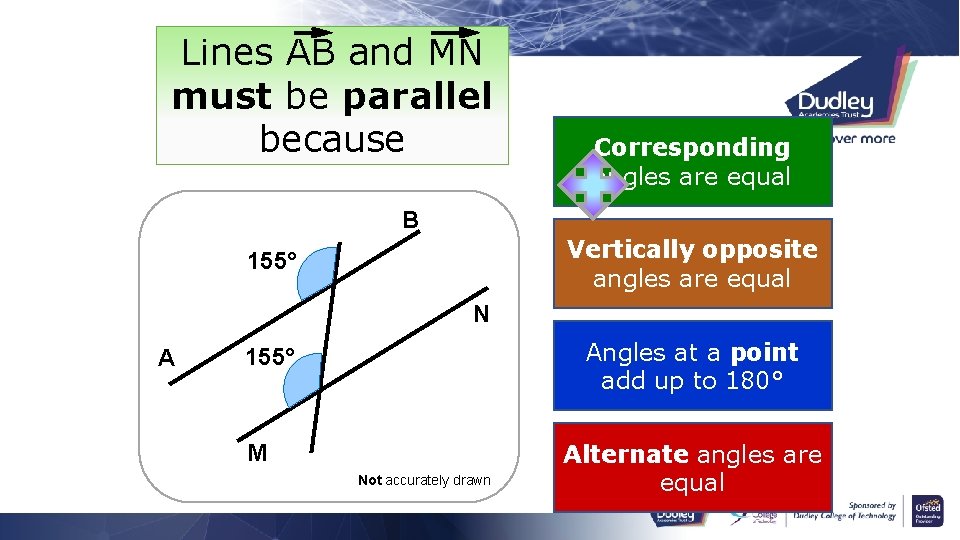
Lines AB and MN must be parallel because Corresponding angles are equal B Vertically opposite angles are equal 155° N A Angles at a point add up to 180° 155° M Not accurately drawn Alternate angles are equal

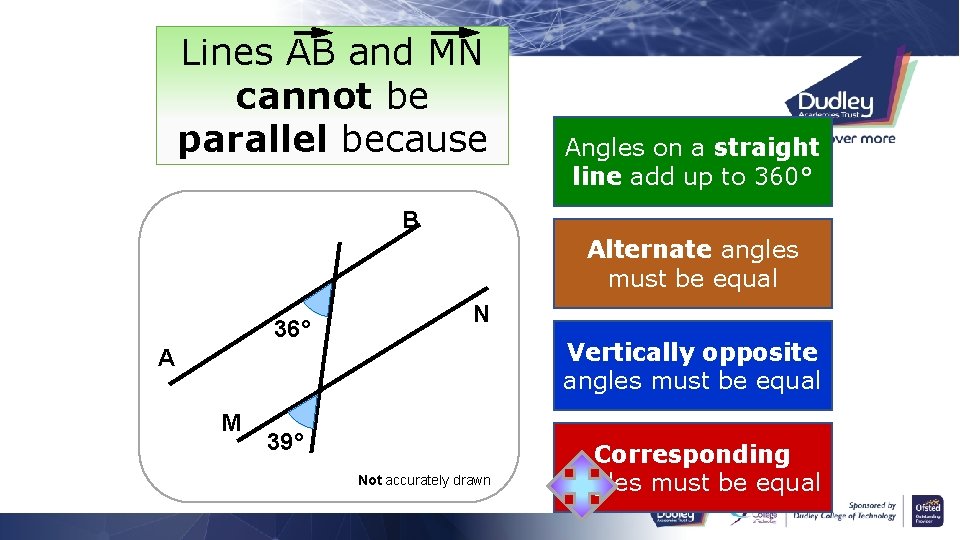
Lines AB and MN cannot be parallel because Angles on a straight line add up to 360° B Alternate angles must be equal 36° N Vertically opposite angles must be equal A M 39° Not accurately drawn Corresponding angles must be equal

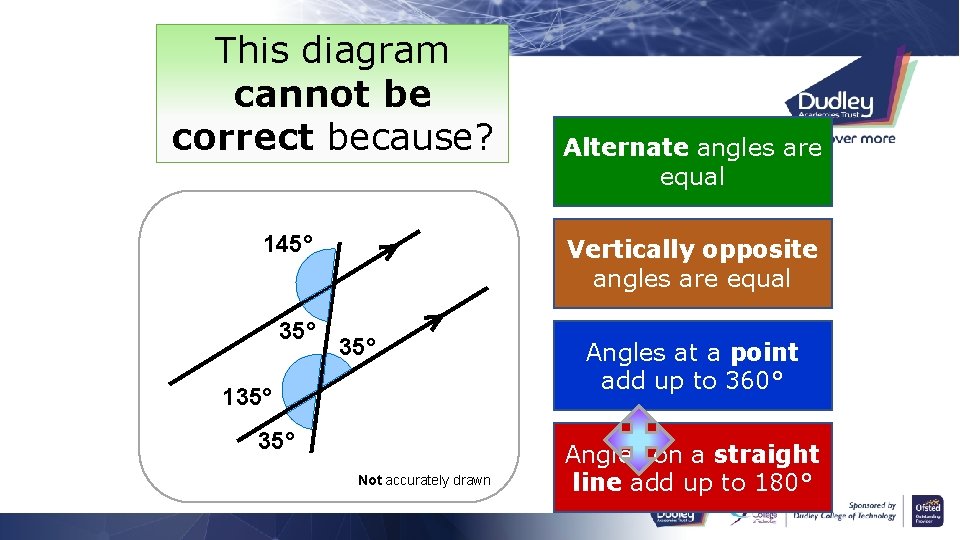
This diagram cannot be correct because? 145° 35° Alternate angles are equal Vertically opposite angles are equal 35° 135° Not accurately drawn Angles at a point add up to 360° Angles on a straight line add up to 180°

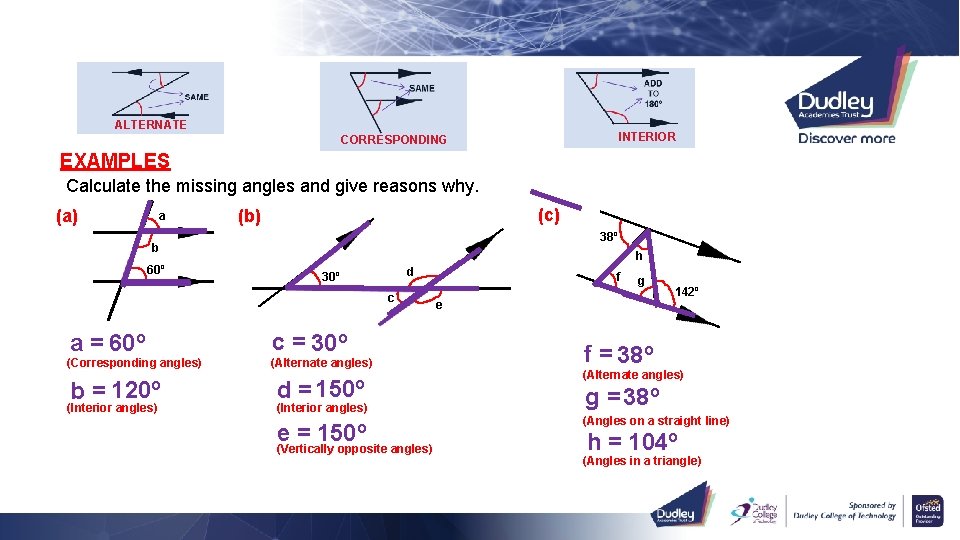
ALTERNATE INTERIOR CORRESPONDING EXAMPLES Calculate the missing angles and give reasons why. (a) a (c) (b) 38º b 60º h d 30º c a = 60º (Corresponding angles) b = 120º (Interior angles) c = 30º (Alternate angles) d = 150º (Interior angles) e = 150º (Vertically opposite angles) f g e 142º f = 38º (Alternate angles) g = 38º (Angles on a straight line) h = 104º (Angles in a triangle)



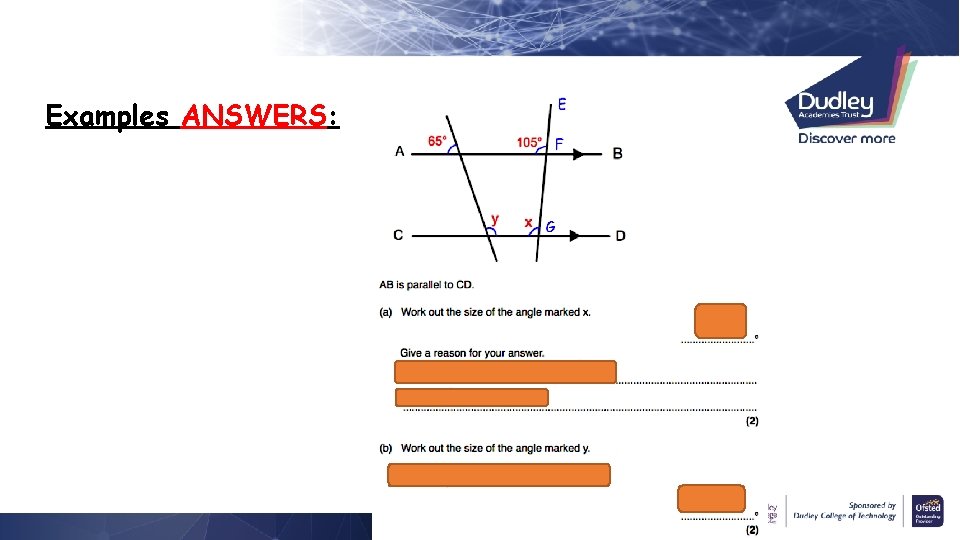
Example 1:

Examples ANSWERS:

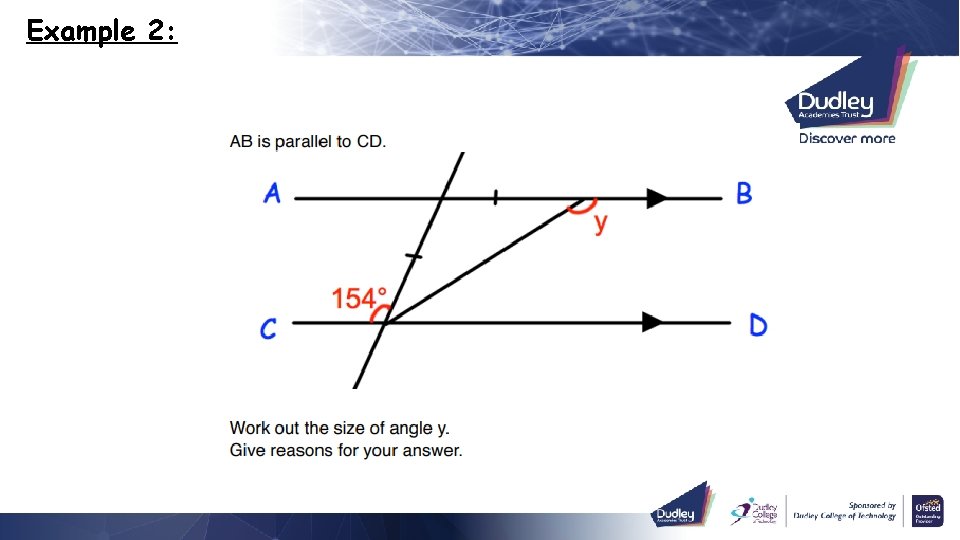
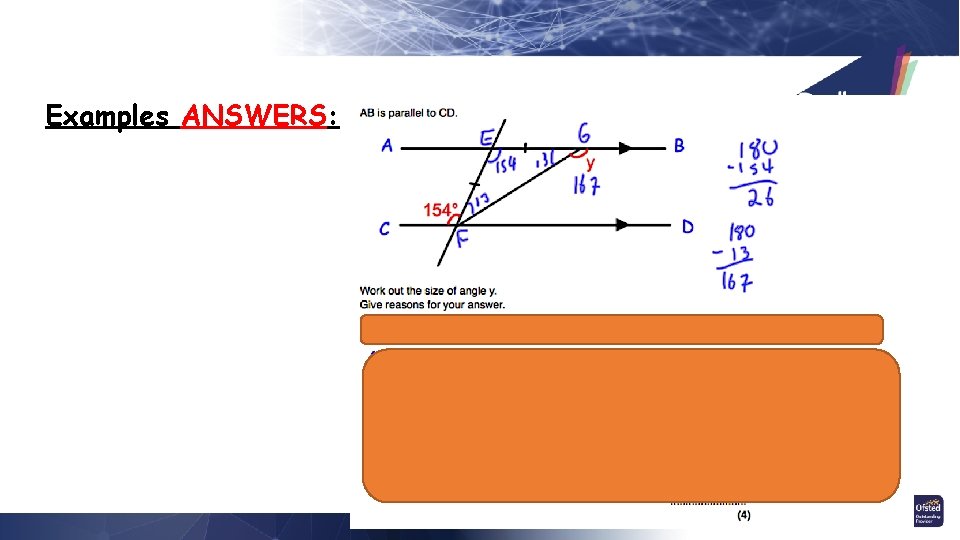
Example 2:

Examples ANSWERS:

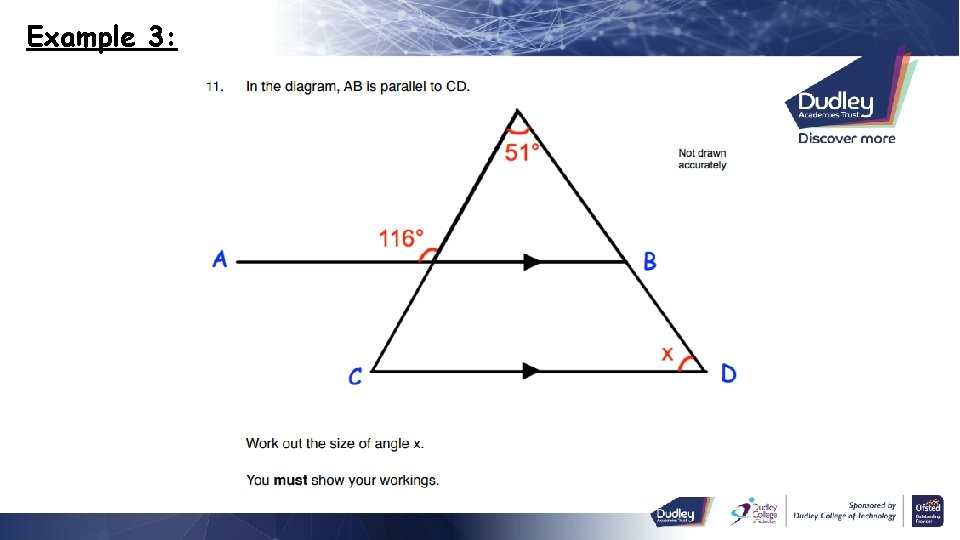
Example 3:

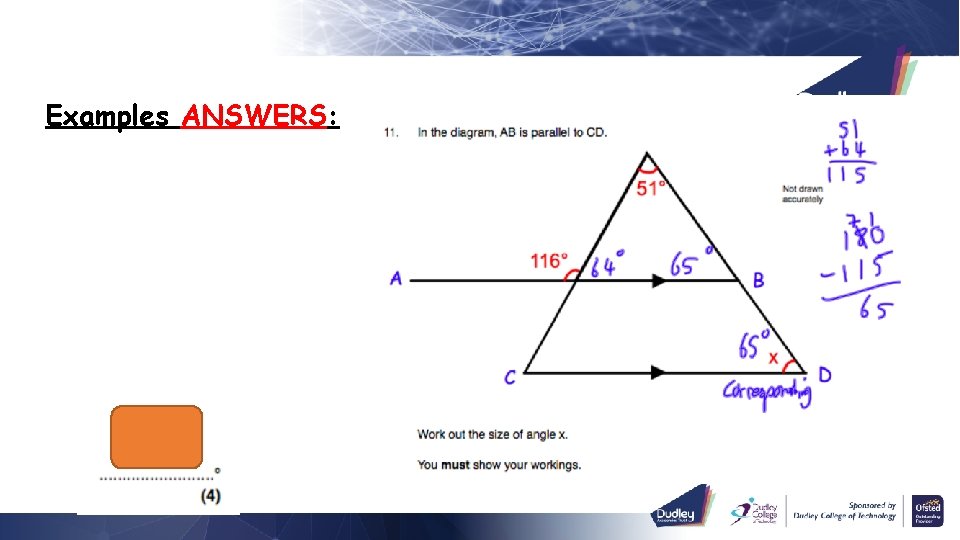
Examples ANSWERS:

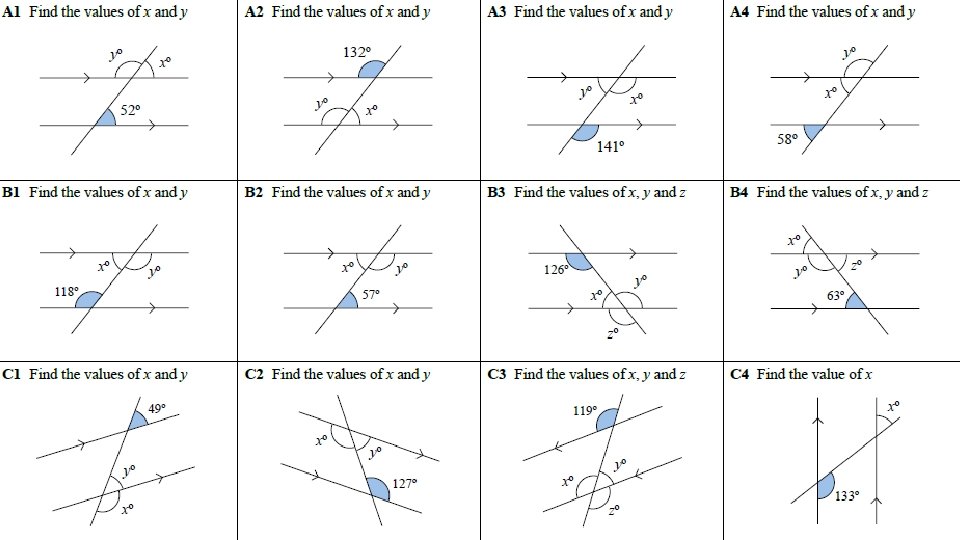
Task 1 or Task 2 Decide on the worksheet they are bronze, silver, gold Make sure you provide reasons for EVERY answer!

Answers task 1 a. x = 112° Cor b. z = 75° Alt c. y = 150° Cor d. x = 99° Opp y = 99° Cor y = 81° Alt line e. x= 106° y= 106°, Cor F x = 123° Cor x = 70° Sup A= B= C= D= E= F= G= H= I= J= g f d c c f f d e e x= 30° sup

Answers task 2 x = 48° Alt z = 42° Sup y = 61° Cor x = 54° Sup x = 96° Cor y = 133° Alt y = 120° Sup z = 58° Line, Alt z = 99° Sup x = 87º Alt y = 109º Quad a = 54º Line, Alt b = 116º Line, Alt n = 54º Cor m = 58º Tri

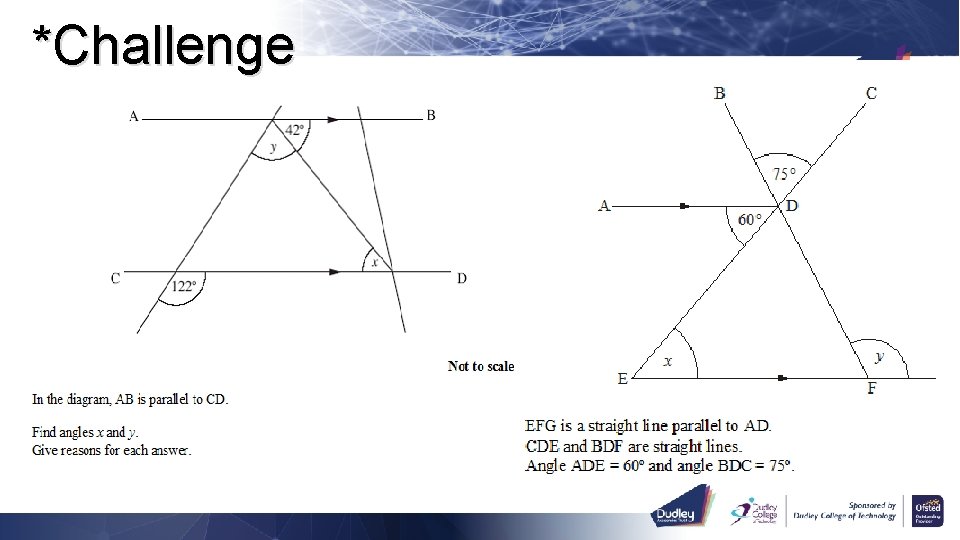
*Challenge

Now try these exam equations in pairs https: //www. mathsgenie. co. uk/resources /33_angles-parallel-lines. pdf

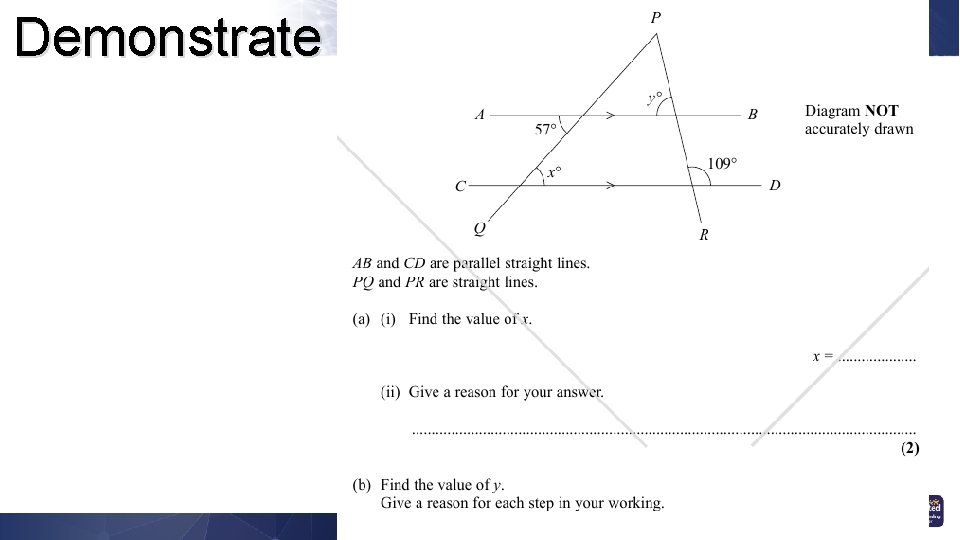
Demonstrate

Demonstrate