Demographic models Lecture 3 Characteristics and properties of

Demographic models Lecture 3. Characteristics and properties of models. Model flexibility and internal consistency. Horizon of modeling, horizon of projection. Types of curves (linear growth, exponential growth, logistic curve). Equilibrium, catastrophe, stabilization. Stability, convergence. Control, regulation. Compatibility with models of another subsystems. Asymptotics, limit theorems and properties. Equilibrium models. Ergodic property. Demographic table as a model. Life table. Concept of model life tables. Brass’s models. Standard life table. UN model life tables. Nuptiality models. Coale-Trussell fertility model. Survival probability, survival curve.

Demographic models Characteristics and properties of models Continuity / discreteness of independent variables Continuity / discreteness and dimension of phase variables Number demographic groups, multistatus models Types of demographic events and a list of transitions Dependence / independence of events Type and set of model equations Time horizon Opportunity to adjust the model parameters Usability for projections, explanations, and research Flexibility and consistency

Demographic models Characteristics and properties of models Continuity / discreteness of independent variables Example: continuous time, continuous age

Demographic models Characteristics and properties of models Dependence / independence of events • • • independence of population behavior in another ages independence of prehistory for one type of demographic events independence of the state in another groups and events for another types independence of the demographic group scale Independence / dependence of random and

Demographic models Curve types Linear growth Exponential growth Logistic curve

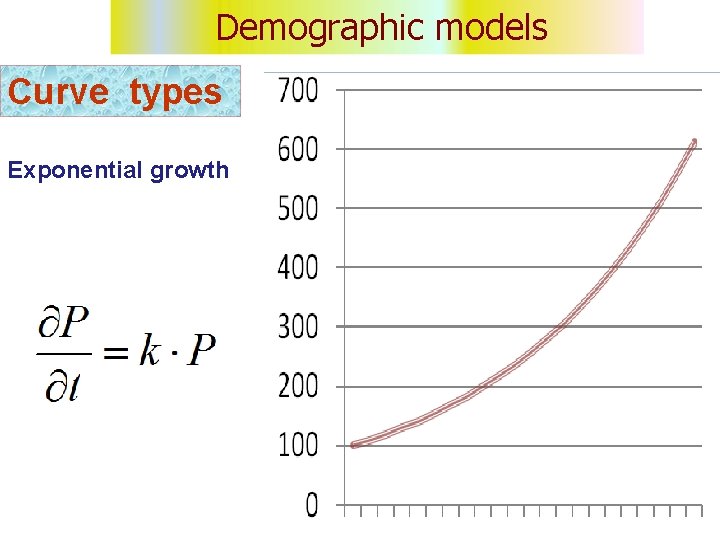
Demographic models Curve types Exponential growth

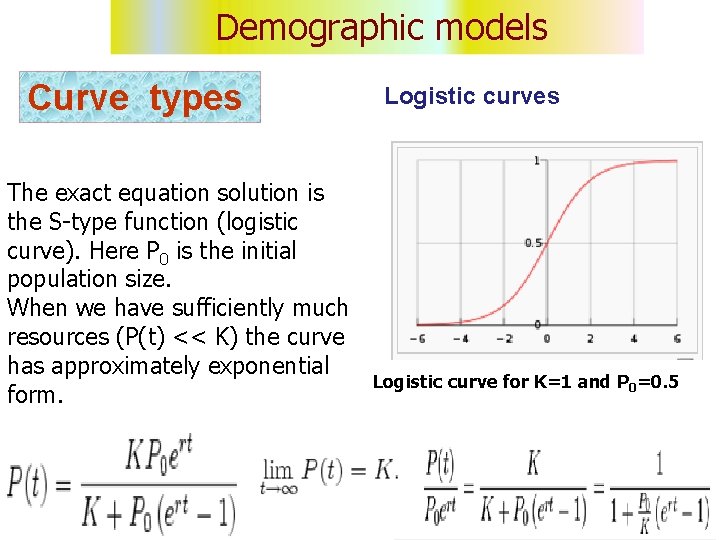
Demographic models Curve types Logistic curves • Speed of population reproduction is proportional to its current size all other conditions being equal. • Speed of population reproduction is proportional to the volume of available resources. Thus the second equation term reflects the competition for these resources which limits population growth. Let P - the size of population, t – time. The model appears as a differential equation where parameter r defines reproduction rate, K – volume of resources, that is the maximal population size.

Demographic models Curve types The exact equation solution is the S-type function (logistic curve). Here P 0 is the initial population size. When we have sufficiently much resources (P(t) << K) the curve has approximately exponential form. Logistic curves Logistic curve for K=1 and P 0=0. 5

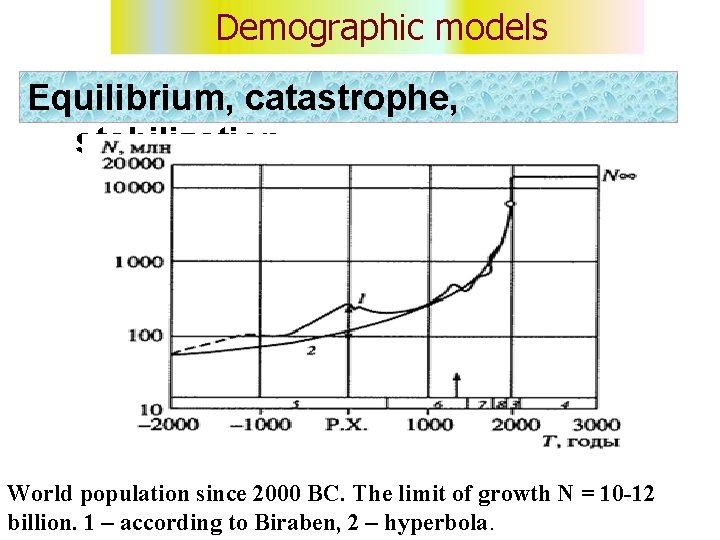
Demographic models Equilibrium, catastrophe, stabilization. World population since 2000 BC. The limit of growth N = 10 -12 billion. 1 – according to Biraben, 2 – hyperbola.

Demographic models Equation of population dynamics

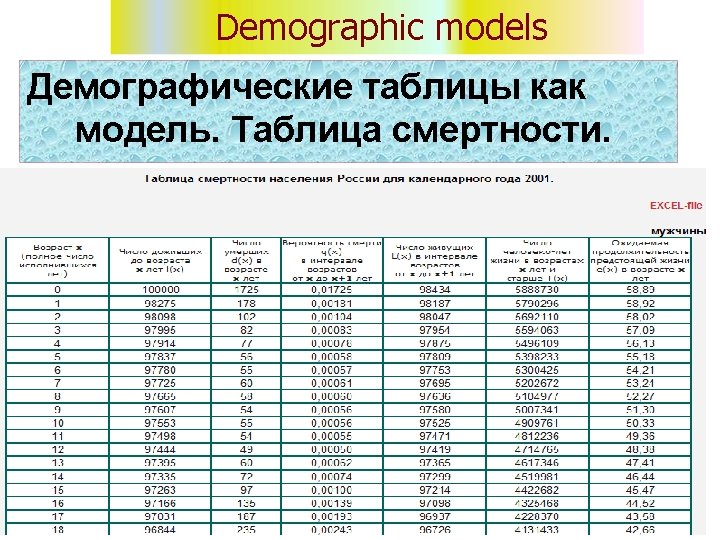
Demographic models Asymptotics, limit theorems and properties. Equilibrium models. Ergodic property. We study using Excel file “model 1. xls”