Demand Management and FORECASTING Operations Management Dr Ron

Demand Management and FORECASTING Operations Management Dr. Ron Lembke

Demand Management • Coordinate sources of demand for supply chain to run efficiently, deliver on time • Independent Demand ▫ Things demanded by end users • Dependent Demand ▫ Demand known, once demand for end items is known

Affecting Demand • Increasing demand ▫ Marketing campaigns ▫ Sales force efforts, cut prices • Changing Timing of demand ▫ Incentives for earlier or later delivery ▫ At capacity, don’t actively pursue more

Predicting the Future We know the forecast will be wrong. Try to make the best forecast we can, ▫ Given the time we want to invest ▫ Given the available data • The “Rules” of Forecasting: 1. The forecast will always be wrong 2. The farther out you are, the worse your forecast is likely to be. 3. Aggregate forecasts are more likely to accurate than individual item ones

Time Horizons Different decisions require projections about different time periods: • Short-range: who works when, what to make each day (weeks to months) • Medium-range: when to hire, lay off (months to years) • Long-range: where to build plants, enter new markets, products (years to decades)

Forecast Impact Finance & Accounting: budget planning Human Resources: hiring, training, laying off employees Capacity: not enough, customers go away angry, too much, costs are too high Supply-Chain Management: bringing in new vendors takes time, and rushing it can lead to quality problems later

Qualitative Methods • Sales force composite / Grass Roots • Market Research / Consumer market surveys & interviews • Jury of Executive Opinion / Panel Consensus • Delphi Method • Historical Analogy - DVDs like VCRs • Naïve approach

Quantitative Methods Time Series Methods 0. All-Time Average 1. Simple Moving Average 2. Weighted Moving Average 3. Exponential Smoothing 4. Exponential smoothing with trend 5. Linear regression Causal Methods Linear Regression

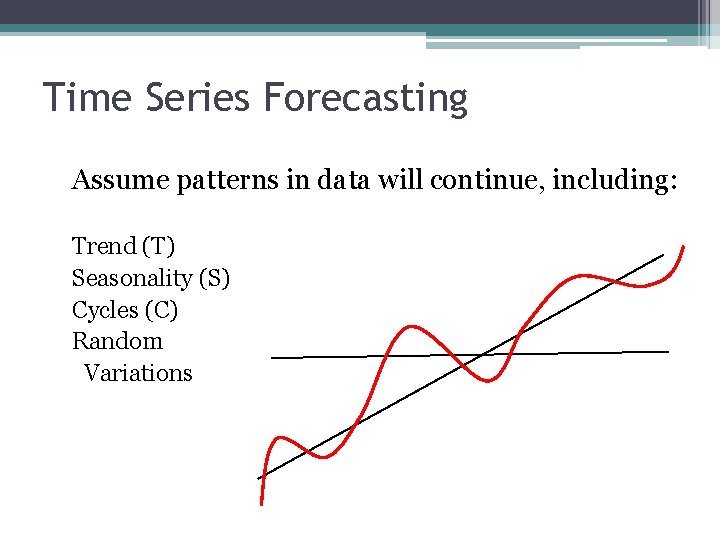
Time Series Forecasting Assume patterns in data will continue, including: Trend (T) Seasonality (S) Cycles (C) Random Variations

All-Time Average To forecast next period, take the average of all previous periods Advantages: Simple to use Disadvantages: Ends up with a lot of data Gives equal importance to very old data

4/7/2009 Farm Angels: Ty: 1. 000, Jacob 0. 833, Noah 0. 667 (6 at bats)

End of 2008 season

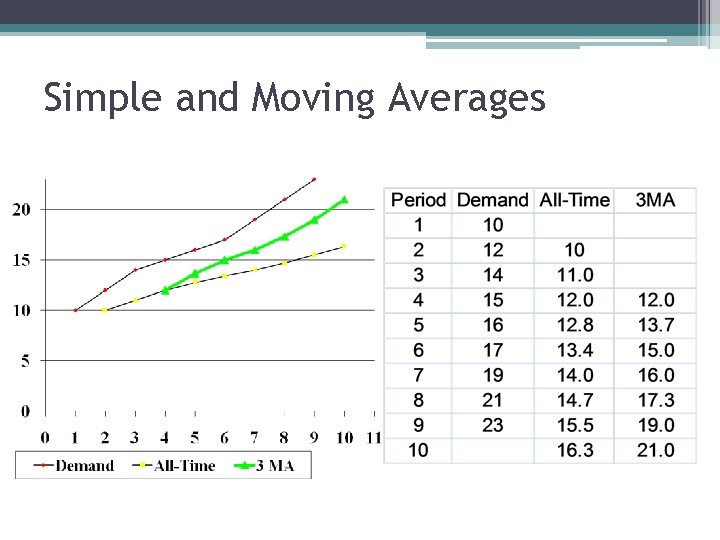
Moving Average Compute forecast using n most recent periods Jan Feb Mar Apr May Jun Jul 3 month Moving Avg: June forecast: FJun = (AMar + AApr + AMay)/3 If no seasonality, freedom to choose n If seasonality is N periods, must use N, 2 N, 3 N etc. number of periods

Moving Average Advantages: ▫ ▫ ▫ Ignores data that is “too” old Requires less data than simple average More responsive than simple average Disadvantages: ▫ ▫ ▫ Still lacks behind trend like simple average, (though not as badly) The larger n is, more smoothing, but the more it will lag The smaller n is, the more over-reaction

Simple and Moving Averages

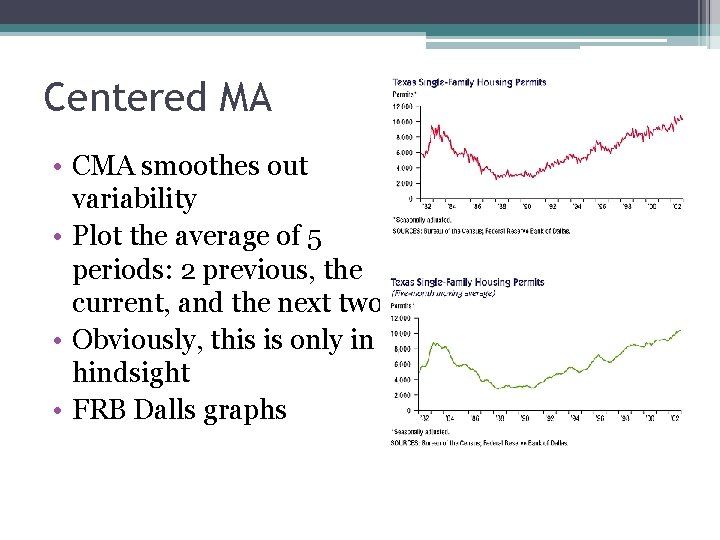
Centered MA • CMA smoothes out variability • Plot the average of 5 periods: 2 previous, the current, and the next two • Obviously, this is only in hindsight • FRB Dalls graphs

Stability vs. Responsiveness • Responsive ▫ Real-time accuracy ▫ Market conditions • Stable ▫ Forecasts being used throughout the company ▫ Long-term decisions based on forecasts ▫ Don’t whipsaw those folks

Old Data Comparison of simple, moving averages clearly shows that getting rid of old data makes forecast respond to trends faster Moving average still lags the trend, but it suggests to us we give newer data more weight, older data less weight.

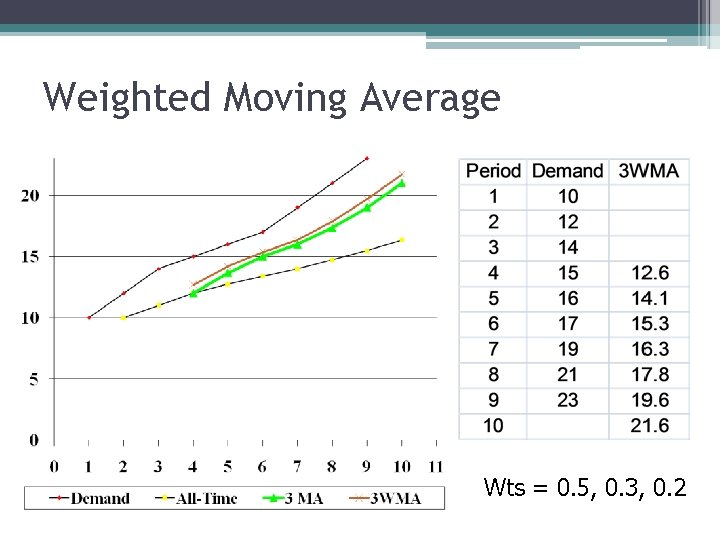
Weighted Moving Average FJun = (AMar + AApr + AMay)/3 = (3 AMar + 3 AApr + 3 AMay)/9 Why not consider: FJun = (2 AMar + 3 AApr + 4 AMay)/9 FJun = 2/9 AMar + 3/9 AApr + 4/9 AMay Ft = w 1 At-3 + w 2 At-2 + w 3 At-1 Complicated: • Have to decide number of periods, and weights for each • Weights have to add up to 1. 0 • Most recent probably most relevant, gets most weight • Carry around n periods of data to make new forecast

Weighted Moving Average Wts = 0. 5, 0. 3, 0. 2

Setting Parameters • Weighted Moving Average ▫ Number of Periods ▫ Individual weights • Trial and Error ▫ Evaluate performance of forecast based on some metric

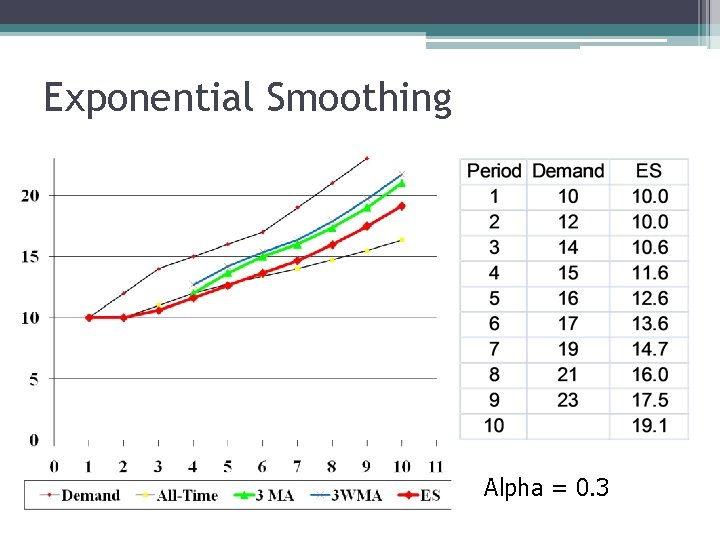
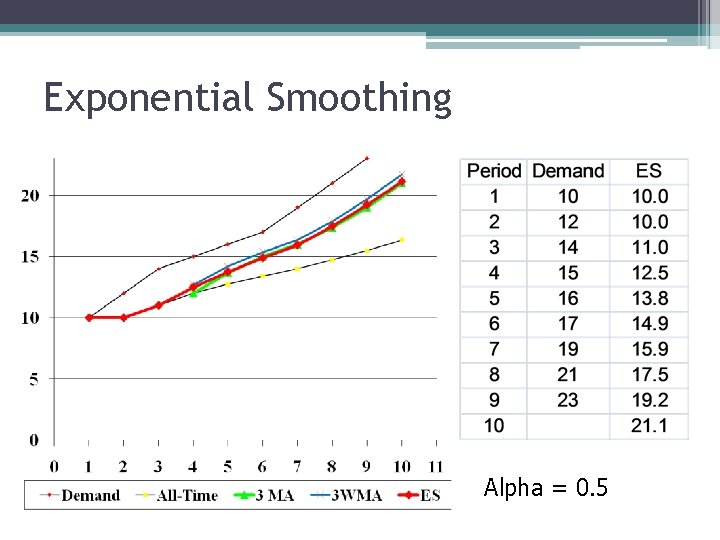
Exponential Smoothing F 10 = F 9 + 0. 2 (A 9 - F 9) F 10 = 0. 8 F 9 + 0. 2 (A 9 - F 9) At-1 Actual demand in period t-1 Forecast for period t-1 Smoothing constant >0, <1 Forecast is old forecast plus a portion of the error of the last forecast. Formulas are equivalent, give same answer

Exponential Smoothing • Smoothing Constant between 0. 1 -0. 3 • Easier to compute than moving average • Most widely used forecasting method, because of its easy use • F 1 = 1, 050, = 0. 05, A 1 = 1, 000 • F 2 = F 1 + (A 1 - F 1) • = 1, 050 + 0. 05(1, 000 – 1, 050) • = 1, 050 + 0. 05(-50) = 1, 047. 5 units • BTW, we have to make a starting forecast to get started. Often, use actual A 1

Exponential Smoothing Alpha = 0. 3

Exponential Smoothing Alpha = 0. 5

Exponential Smoothing We take: And substitute in to get: and if we continue doing this, we get: Older demands get exponentially less weight

Choosing • Low : if demand is stable, we don’t want to get thrown into a wild-goose chase, over-reacting to “trends” that are really just short-term variation • High : If demand really is changing rapidly, we want to react as quickly as possible

Averaging Methods • • Simple Average Moving Average Weighted Moving Average Exponentially Weighted Moving Average (Exponential Smoothing) • They ALL take an average of the past ▫ With a trend, all do badly ▫ Average must be in-between 30 20 10

Trend-Adjusted Ex. Smoothing

Trend-Adjusted Ex. Smoothing Trend-Adjusted Forecast for period 2 was Suppose actual demand is 115, A 2=115

Trend-Adjusted Ex. Smoothing Suppose actual demand is 120, A 3=120

TAF 6=F 5+T 5 A 5 F 6

Selecting and β • You could: ▫ Try an initial value for each parameter. ▫ Try lots of combinations and see what looks best. ▫ But how do we decide “what looks best? ” • Let’s measure the amount of forecast error. • Then, try lots of combinations of parameters in a methodical way. ▫ Let = 0 to 1, increasing by 0. 1 For each value, try = 0 to 1, increasing by 0. 1

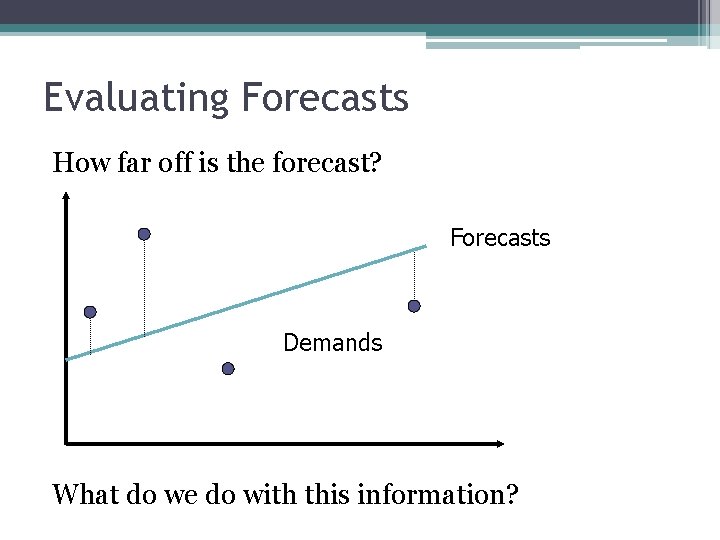
Evaluating Forecasts How far off is the forecast? Forecasts Demands What do we do with this information?

Measuring the Errors Period A-F Method 1 A-F Method 2 1 100 10 2 -100 10 3 100 10 4 -100 10 5 100 10 6 -100 10 7 100 10 8 -100 10 9 100 10 10 -100 10 RSFE 0 100 • Method 1 forecasts are low, high, etc. • Method 2 forecasts always too low. • Running Sum of Forecast Errors, RSFE ▫ Sum of all periods ▫ Also known as the Bias

Evaluating Forecasts Mean Absolute Deviation Mean Squared Error Mean Absolute Percent Error

MAD of examples Period |A-F| Method 1 |A-F| Method 2 1 100 10 2 100 10 3 100 10 4 100 10 5 100 10 6 100 10 7 100 10 8 100 10 9 100 10 10 10 MAD 100 10 • MAD shows that method 1 is off by a larger amount • Method 2 was biased • However, overall, Method 2 seems preferable

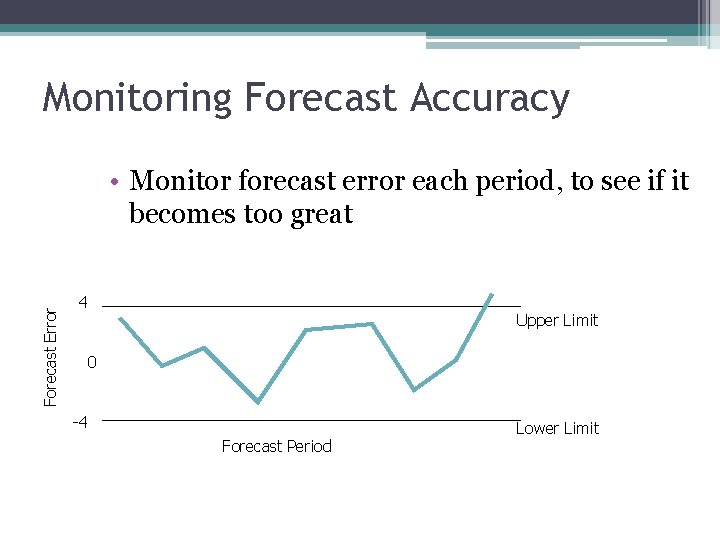
Tracking Signal • To monitor, compute tracking signal • If >4 or <-4 something is wrong • Top should sum to 0 over time. If not, forecast is biased.

Monitoring Forecast Accuracy Forecast Error • Monitor forecast error each period, to see if it becomes too great 4 Upper Limit 0 -4 Forecast Period Lower Limit

Techniques for Trend • Determine how demand increases as a function of time t = periods since beginning of data b = Slope of the line a = Value of yt at t = 0

Computing Values

Linear Regression • Four methods 1. Type in formulas for trend, intercept 2. Tools | Data Analysis | Regression 3. Graph, and R click on data, add a trendline, and display the equation. 4. Use intercept(Y, X), slope(Y, X) and RSQ(Y, X) commands • Fits a trend and intercept to the data. • R 2 measures the percentage of change in y that can be explained by changes in x. • Gives all data equal weight. • Exp. smoothing with a trend gives more weight to recent, less to old.

Causal Forecasting • Linear regression seeks a linear relationship between the input variable and the output quantity. • For example, furniture sales correlates to housing sales • Not easy, multiple sources of error: ▫ Understand quantify relationship ▫ Someone else has to forecast the x values for you

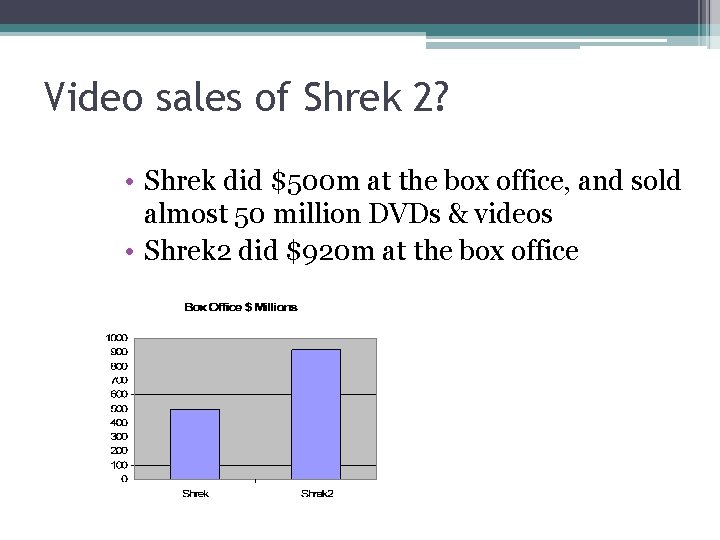
Video sales of Shrek 2? • Shrek did $500 m at the box office, and sold almost 50 million DVDs & videos • Shrek 2 did $920 m at the box office

Video sales of Shrek 2? • Assume 1 -1 ratio: • • ▫ 920/500 = 1. 84 ▫ 1. 84 * 50 million = 92 million videos? ▫ Fortunately, not that dumb. January 3, 2005: 37 million sold! March analyst call: 40 m by end Q 1 March SEC filing: 33. 7 million sold. Oops. May 10 Announcement: ▫ In 2 nd public Q, missed earnings targets by 25%. ▫ May 9, word started leaking ▫ Stock dropped 16. 7%

Lessons Learned • Flooded market with DVDs • Guaranteed Sales ▫ Promised the retailer they would sell them, or else the retailer could return them ▫ Didn’t know how many would come back • 5 years ago ▫ Typical movie 30% of sales in first week ▫ Animated movies even lower than that • 2004/5 50 -70% in first week ▫ Shrek 2: 12. 1 m in first 3 days ▫ American Idol ending, had to vote in first week

The Human Element • Colbert says you have more nerve endings in your gut than in your brain • Limited ability to include factors ▫ Can’t include everything • If it feels really wrong to your gut, maybe your gut is right

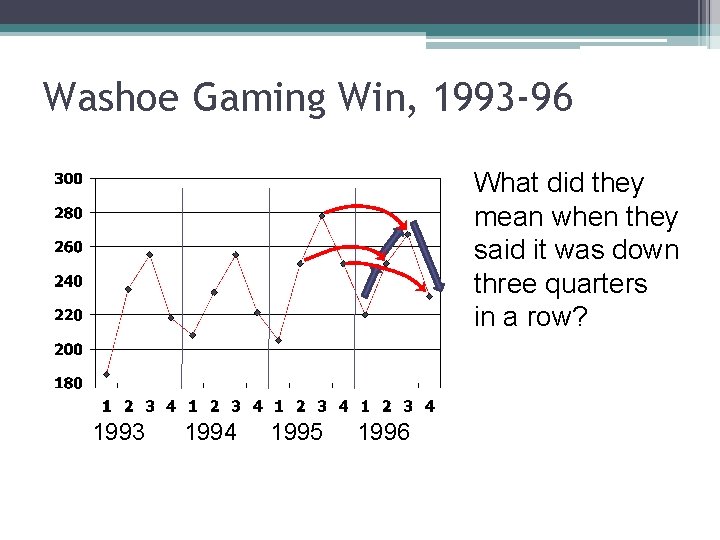
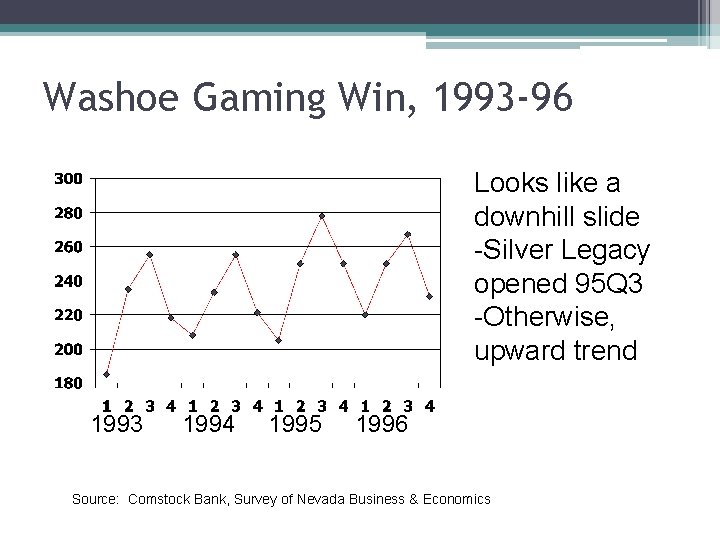
Washoe Gaming Win, 1993 -96 What did they mean when they said it was down three quarters in a row? 1993 1994 1995 1996

Seasonality • Seasonality is regular up or down movements in the data • Can be hourly, daily, weekly, yearly • Naïve method ▫ N 1: Assume January sales will be same as December ▫ N 2: Assume this Friday’s ticket sales will be same as last

Seasonal Relatives • Seasonal relative for May is 1. 20, means May sales are typically 20% above the average • Factor for July is 0. 90, meaning July sales are typically 10% below the average

Seasonality & No Trend Spring Summer Fall Winter Total Avg Sales Relative 200/250 = 0. 8 350350/250 = 1. 4 300/250 = 1. 2 150/250 = 0. 6 1, 000/4=250

Seasonality & No Trend If we expected total demand for the next year to be 1, 100, the average per quarter would be 1, 100/4=275 Forecast Spring 275 * 0. 8 = 220 Summer 275 * 1. 4 = 385 Fall 275 * 1. 2 = 330 Winter 275 * 0. 6 = 165 Total 1, 100

Trend & Seasonality • Deseasonalize to find the trend 1. Calculate seasonal factors 2. Deseasonalize the demand 3. Find trend of deseasonalized line • Project trend into the future 4. Project trend line into future 5. Multiply trend line by seasonal component.

Washoe Gaming Win, 1993 -96 Looks like a downhill slide -Silver Legacy opened 95 Q 3 -Otherwise, upward trend 1993 1994 1995 1996 Source: Comstock Bank, Survey of Nevada Business & Economics

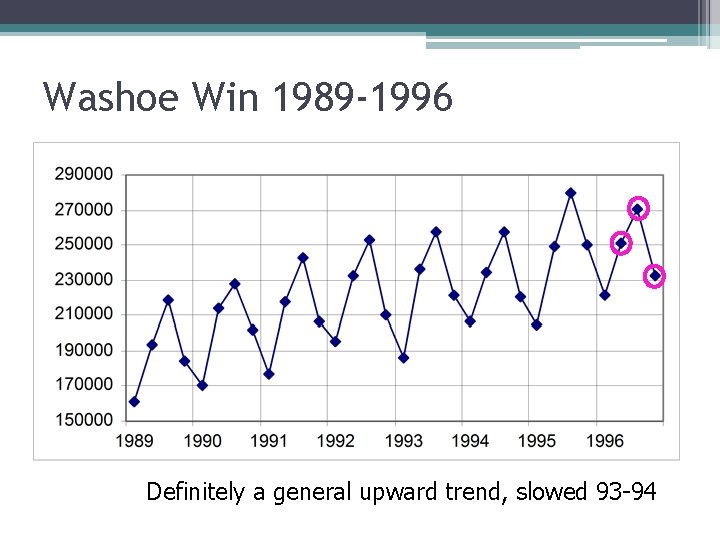
Washoe Win 1989 -1996 Definitely a general upward trend, slowed 93 -94

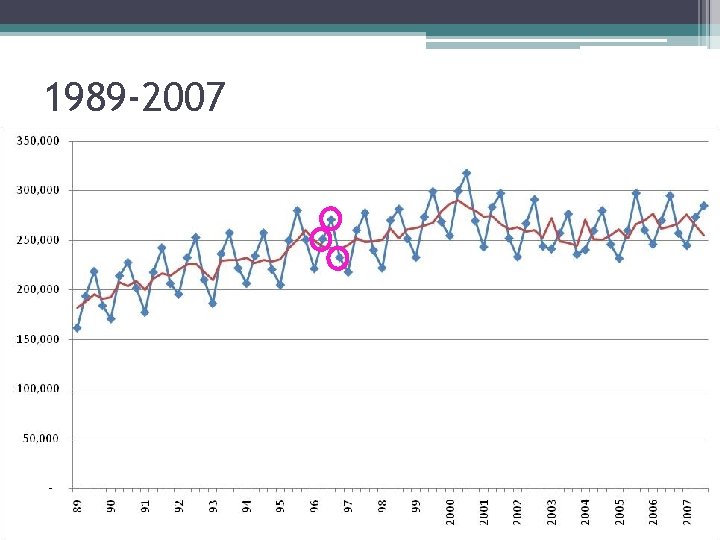
1989 -2007

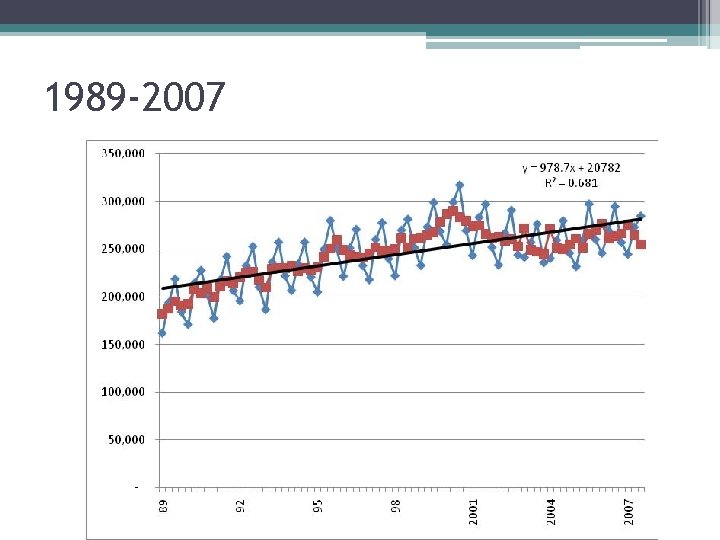
1989 -2007

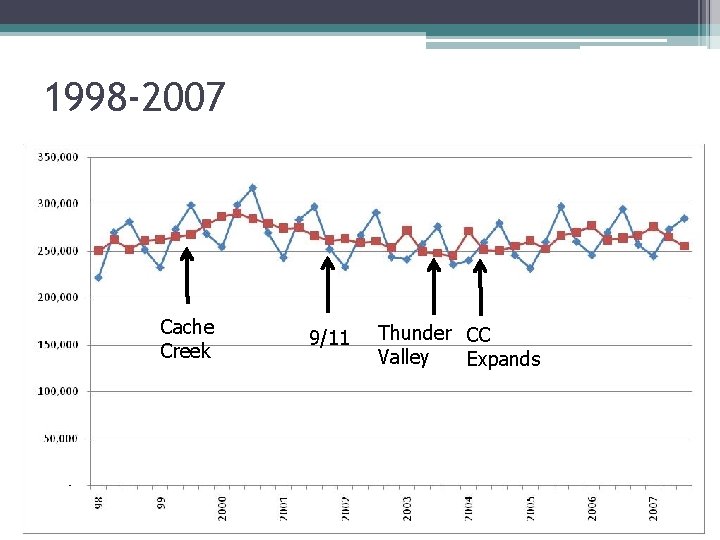
1998 -2007 Cache Creek 9/11 Thunder CC Valley Expands

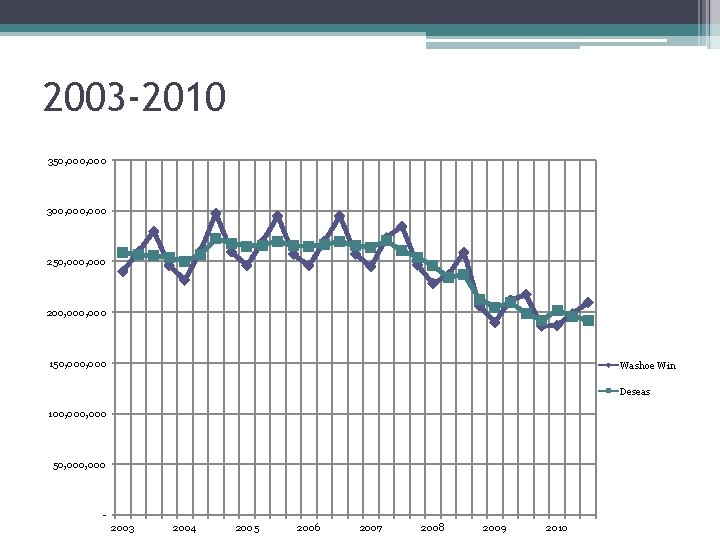
2003 -2010 350, 000 300, 000 250, 000 200, 000 150, 000 Washoe Win Deseas 100, 000 50, 000 2003 2004 2005 2006 2007 2008 2009 2010

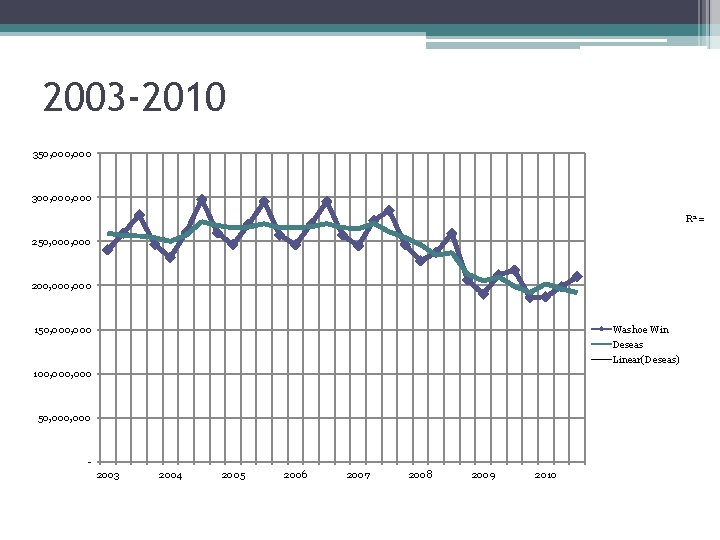
2003 -2010 350, 000 300, 000 R 2 = 0. 6 250, 000 200, 000 Washoe Win 150, 000 Deseas Linear(Deseas) 100, 000 50, 000 2003 2004 2005 2006 2007 2008 2009 2010

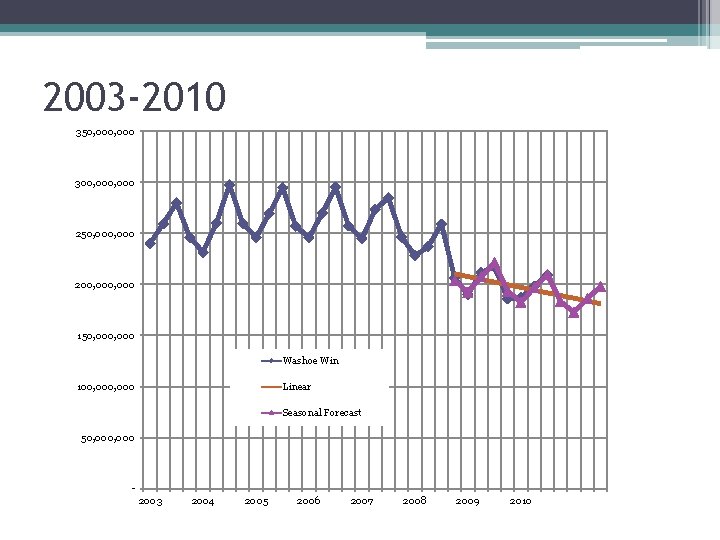
2003 -2010 350, 000 300, 000 250, 000 200, 000 150, 000 Washoe Win 100, 000 Linear Seasonal Forecast 50, 000 2003 2004 2005 2006 2007 2008 2009 2010

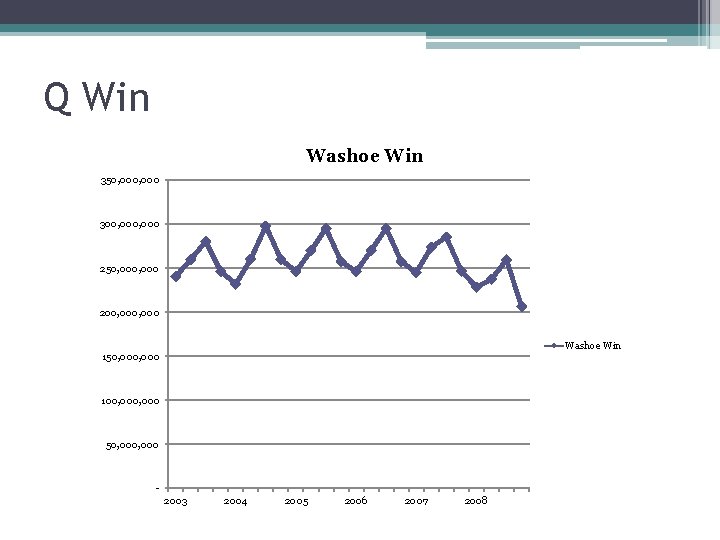
Q Win Washoe Win 350, 000 300, 000 250, 000 200, 000 Washoe Win 150, 000 100, 000 50, 000 2003 2004 2005 2006 2007 2008

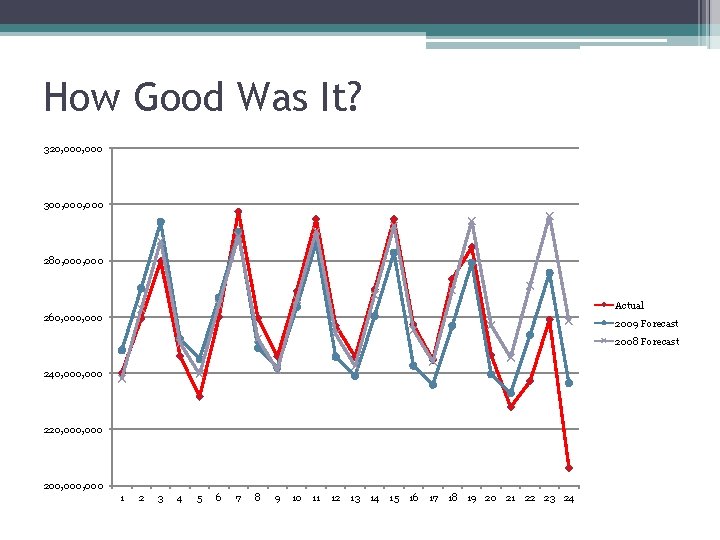
How Good Was It? 320, 000 300, 000 280, 000 Actual 260, 000 2009 Forecast 2008 Forecast 240, 000 220, 000 200, 000 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Summary 1. Calculate indexes 2. Deseasonalize 1. Divide actual demands by seasonal indexes 3. Do a LR 4. Project the LR into the future 5. Seasonalize 1. Multiply straight-line forecast by indexes