Demand Forecasting Four Fundamental Approaches Time Series General

Demand Forecasting • Four Fundamental Approaches • Time Series ��� – General Concepts – Evaluating Forecasts – How ‘good’ is it? – Forecasting Methods (Stationary) � • • Cumulative Mean � Naïve Forecast �� ����� Moving Average Exponential Smoothing • • OLS Regression Holt’s Method Exponential Method for Seasonal Data Winter’s Model Other Models – Forecasting Methods (Trends & Seasonality)

Demand Forecasting • • Forecasting is difficult – especially for the future Forecasts are always wrong The less aggregated, the lower the accuracy The longer the time horizon, the lower the accuracy The past is usually a pretty good place to start Everything exhibits seasonality of some sort A good forecast is not just a number – it should include a range, description of distribution, etc. • Any analytical method should be supplemented by external information • A forecast for one function in a company might not be useful to another function (Sales to Mkt to Mfg to Trans)

Four Fundamental Approaches Subjective Objective – Judgmental – Causal / Relational • Sales force surveys • Delphi techniques • Jury of experts – Experimental • Customer surveys • Focus group sessions • Test Marketing • Econometric Models • Leading Indicators • Input-Output Models – Time Series • “Black Box” Approach • Uses past to predict the future

Time Series Concepts 1. 2. 3. 4. 5. 6. Time Series – Regular & recurring basis to forecast Stationarity – Values hover around a mean Trend- Persistent movement in one direction Seasonality – Movement periodic to calendar Cycle – Periodic movement not tied to calendar Pattern + Noise – Predictable and random components of a Time Series forecast 7. Generating Process –Equation that creates TS 8. Accuracy and Bias – Closeness to actual vs Persistent tendency to over or under predict 9. Fit versus Forecast – Tradeoff between accuracy to past forecast to usefulness of predictability 10. Forecast Optimality – Error is equal to the random noise

Evaluating Forecasts • • • Visual Review Errors Measure MPE and MAPE Tracking Signal

Demand Forecasting • Generate the large number of short-term, SKU level, locally dis-aggregated demand forecasts required for production, logistics, and sales to operate successfully. � • Focus on: ���� � – – – Forecasting product demand Mature products (not new product releases) Short time horizon (weeks, months, quarters, year) Use of models to assist in the forecast Cases where demand of items is independent

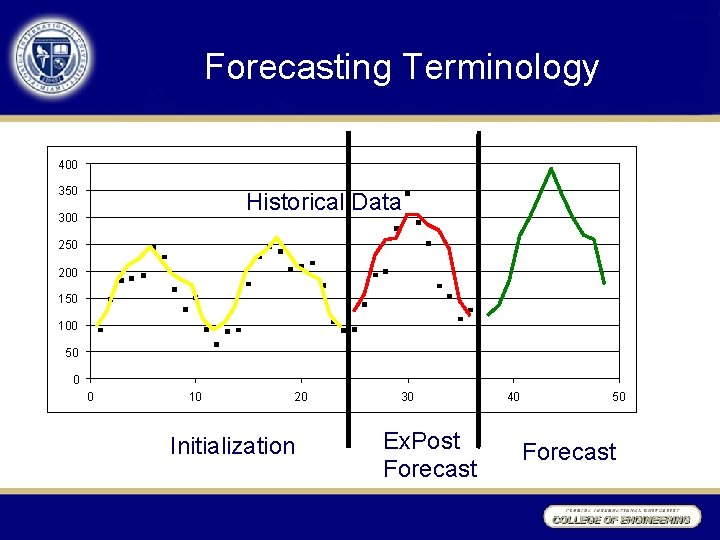
Forecasting Terminology 400 350 Historical Data 300 250 200 150 100 50 0 0 10 20 Initialization 30 Ex. Post Forecast 40 50 Forecast

Forecasting Terminology “We are now looking at a future from here, and the future we were looking at in February now includes some of our past, and we can incorporate the past into our forecast. 1993, the first half, which is now the past and was the future when we issued our first forecast, is now over” Laura D’Andrea Tyson, Head of the President’s Council of Economic Advisors, quoted in November of 1993 in the Chicago Tribune, explaining why the Administration reduced its projections of economic growth to 2 percent from the 3. 1 percent it predicted in February.

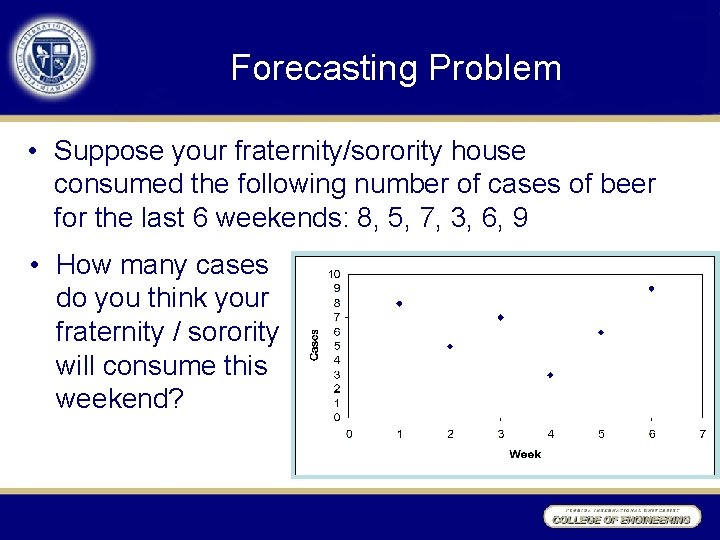
Forecasting Problem • Suppose your fraternity/sorority house consumed the following number of cases of beer for the last 6 weekends: 8, 5, 7, 3, 6, 9 • How many cases do you think your fraternity / sorority will consume this weekend?

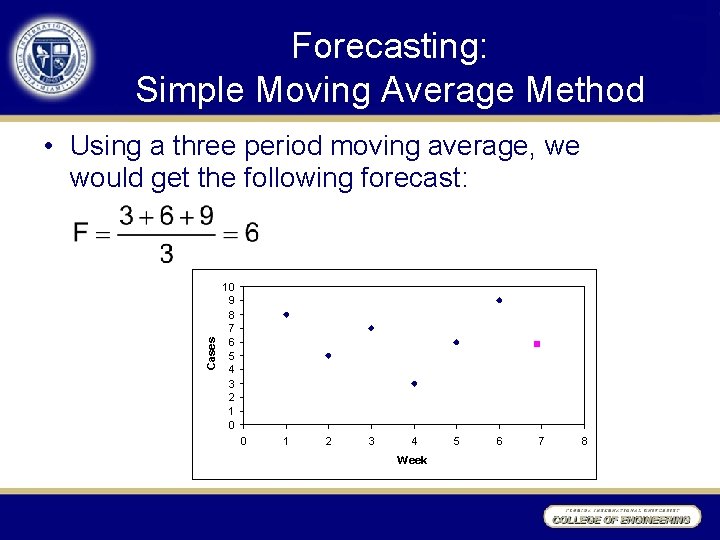
Forecasting: Simple Moving Average Method Cases • Using a three period moving average, we would get the following forecast: 10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 Week 5 6 7 8

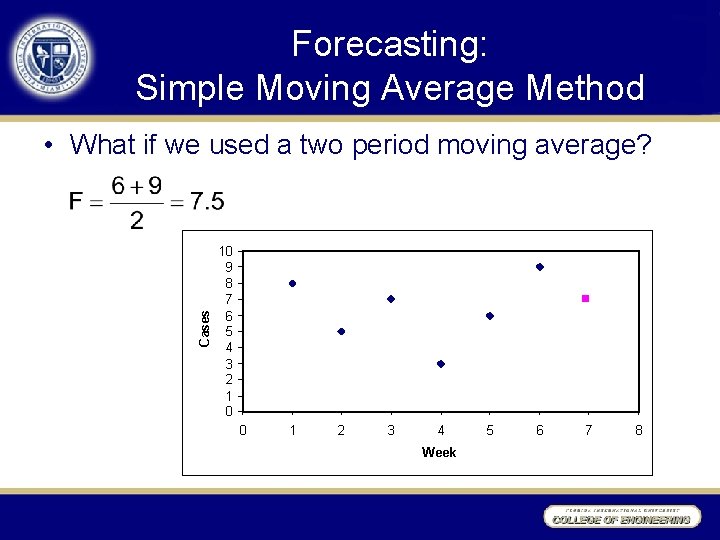
Forecasting: Simple Moving Average Method Cases • What if we used a two period moving average? 10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 Week 5 6 7 8

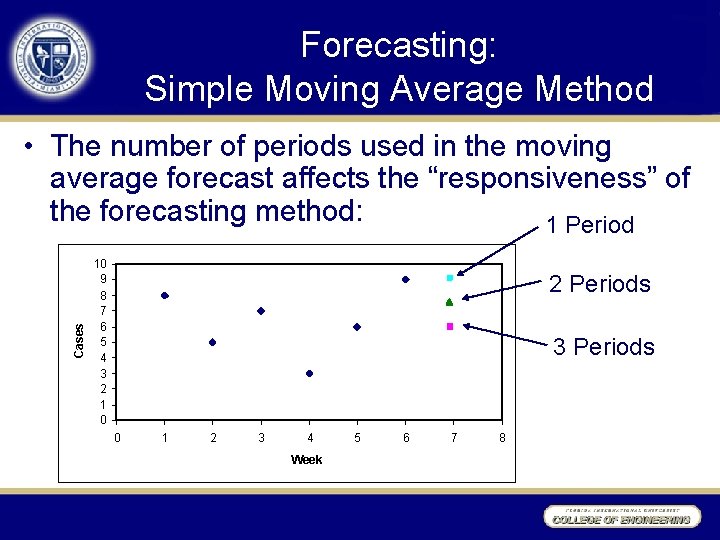
Forecasting: Simple Moving Average Method Cases • The number of periods used in the moving average forecast affects the “responsiveness” of the forecasting method: 1 Period 10 9 8 7 6 5 4 3 2 1 0 2 Periods 3 Periods 0 1 2 3 4 Week 5 6 7 8

Forecasting Terminology • Applying this terminology to our problem using the Moving Average forecast: Initialization Ex. Post Forecast Model Evaluation

Forecasting: Weighted Moving Average Method • Rather than equal weights, it might make sense to use weights which favor more recent consumption values. • With the Weighted Moving Average, we have to select weights that are individually greater than zero and less than 1, and as a group sum to 1: • Valid Weights: (. 5, . 3, . 2) , (. 6, . 3, . 1), (1/2, 1/3, 1/6) • Invalid Weights: (. 5, . 2, . 1), (. 6, -. 1, . 5), (. 5, . 4, . 3, . 2)

Forecasting: Weighted Moving Average Method • A Weighted Moving Average forecast with weights of (1/6, 1/3, 1/2), is performed as follows: • How do you make the Weighted Moving Average forecast more responsive?

Forecasting: Exponential Smoothing • Exponential Smoothing is designed to give the benefits of the Weighted Moving Average forecast without the cumbersome problem of specifying weights. In Exponential Smoothing, there is only one parameter ( ): = smoothing constant (between 0 and 1)

Forecasting: Exponential Smoothing Initialization: • •

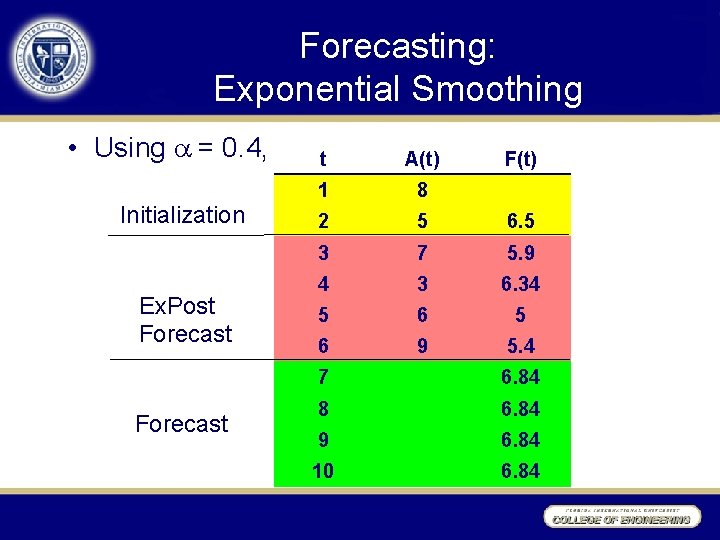
Forecasting: Exponential Smoothing • Using = 0. 4, Initialization Ex. Post Forecast t A(t) F(t) 1 8 2 5 6. 5 3 7 5. 9 4 3 6. 34 5 6 9 5. 4 7 6. 84 8 6. 84 9 6. 84 10 6. 84

Forecasting: Exponential Smoothing

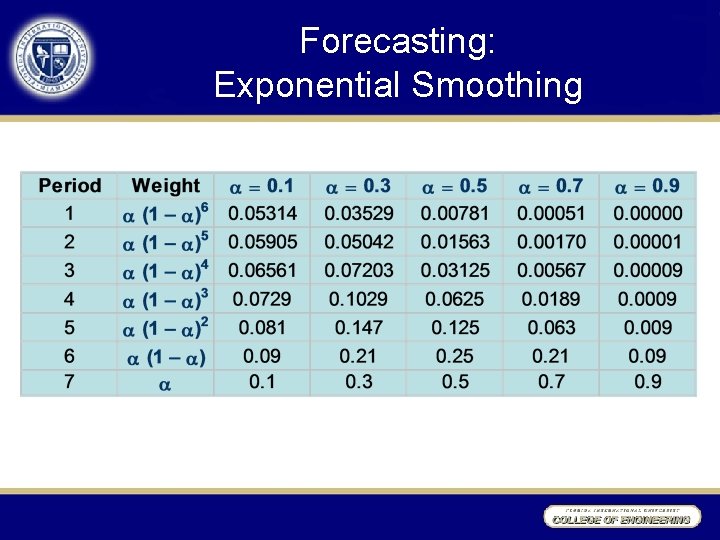
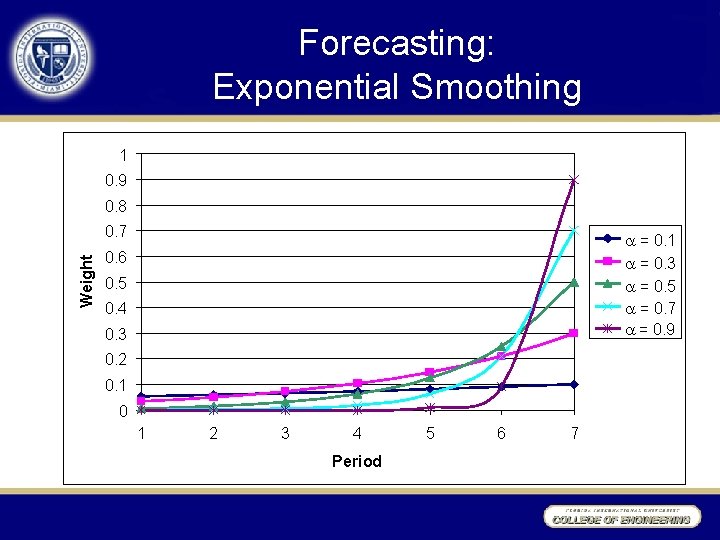
Forecasting: Exponential Smoothing 1 0. 9 0. 8 Weight 0. 7 0. 4 = 0. 1 = 0. 3 = 0. 5 = 0. 7 0. 3 = 0. 9 0. 6 0. 5 0. 2 0. 1 0 1 2 3 4 Period 5 6 7

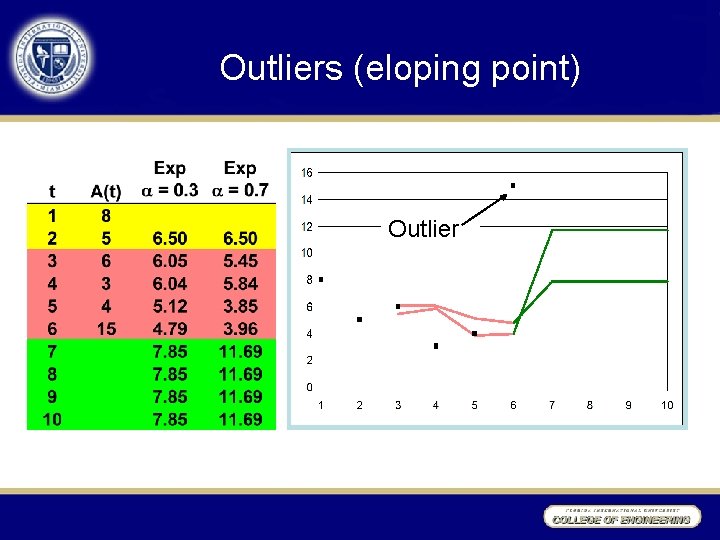
Outliers (eloping point) Outlier

Data with Trends

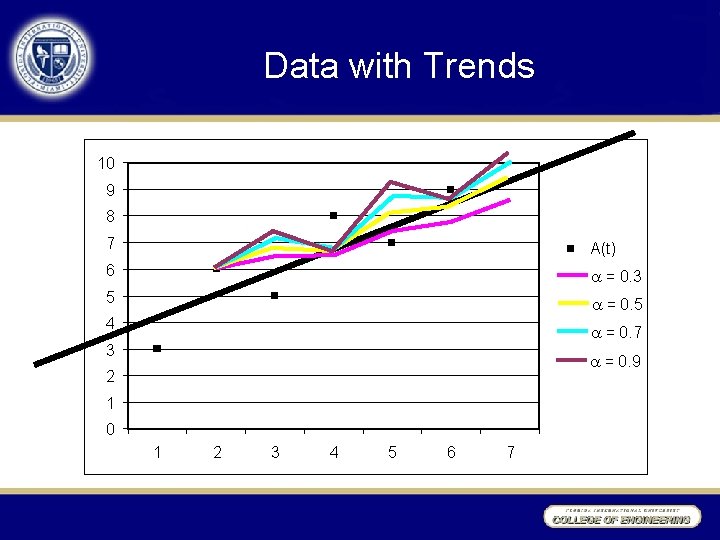
Data with Trends 10 9 8 7 A(t) 6 = 0. 3 5 = 0. 5 4 = 0. 7 3 = 0. 9 2 1 0 1 2 3 4 5 6 7

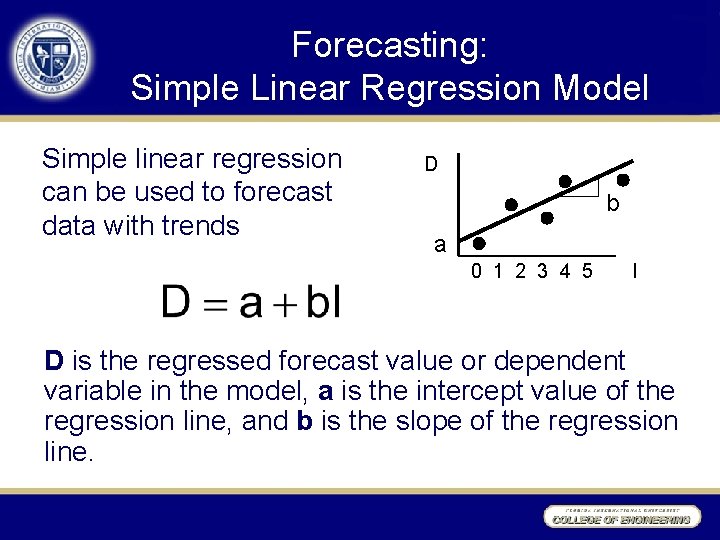
Forecasting: Simple Linear Regression Model Simple linear regression can be used to forecast data with trends D b a 0 1 2 3 4 5 I D is the regressed forecast value or dependent variable in the model, a is the intercept value of the regression line, and b is the slope of the regression line.

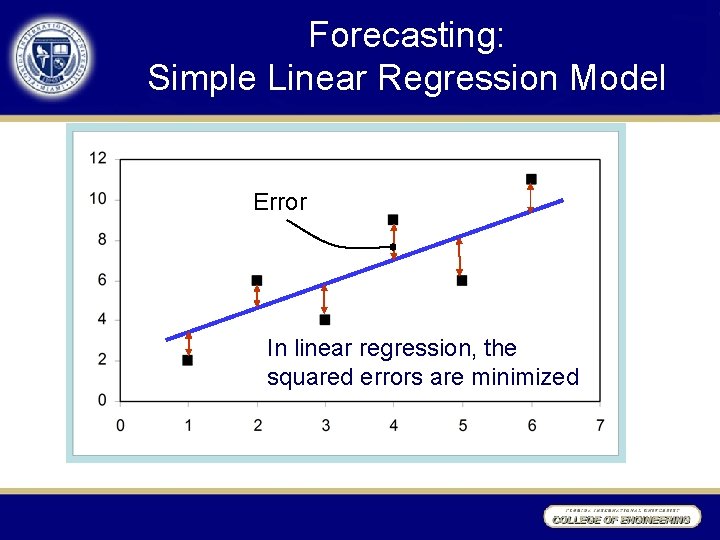
Forecasting: Simple Linear Regression Model Error In linear regression, the squared errors are minimized

Forecasting: Simple Linear Regression Model

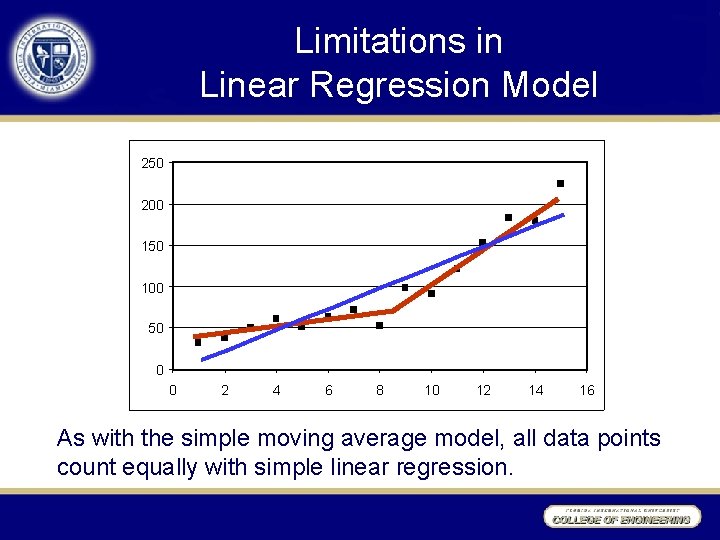
Limitations in Linear Regression Model 250 200 150 100 50 0 0 2 4 6 8 10 12 14 16 As with the simple moving average model, all data points count equally with simple linear regression.

Forecasting: Holt’s Trend Model • To forecast data with trends, we can use an exponential smoothing model with trend, frequently known as Holt’s model: L(t) = A(t) + (1 - ) F(t) T(t) = [L(t) - L(t-1) ] + (1 - ) T(t-1) F(t+1) = L(t) + T(t) • We could use linear regression to initialize the model

Holt’s Trend Model: Initialization First, we’ll initialize the model: L(4) = 20. 5+4(9. 9)=60. 1 T(4) = 9. 9

Holt’s Trend Model: Updating 52 6 64. 6 7. 74 = 0. 3 = 0. 4 72. 34 L(t) = A(t) + (1 - ) F(t) L(5) = 0. 3 (52) + 0. 7 (70)=64. 6 T(t) = [L(t) - L(t-1) ] + (1 - ) T(t-1) T(5) = 0. 4 [64. 6 – 60. 1] + 0. 6 (9. 9) = 7. 74 F(t+1) = L(t) + T(t) F(6) = 64. 6 + 7. 74 = 72. 34

Holt’s Trend Model: Updating = 0. 3 = 0. 4 7 63 72 69. 54 6. 62 76. 16 L(6) = 0. 3 (63) + 0. 7 (72. 34)=69. 54 T(6) = 0. 4 [69. 54 – 64. 60] + 0. 6 (7. 74) = 6. 62 F(7) = 69. 54 + 6. 62 = 76. 16

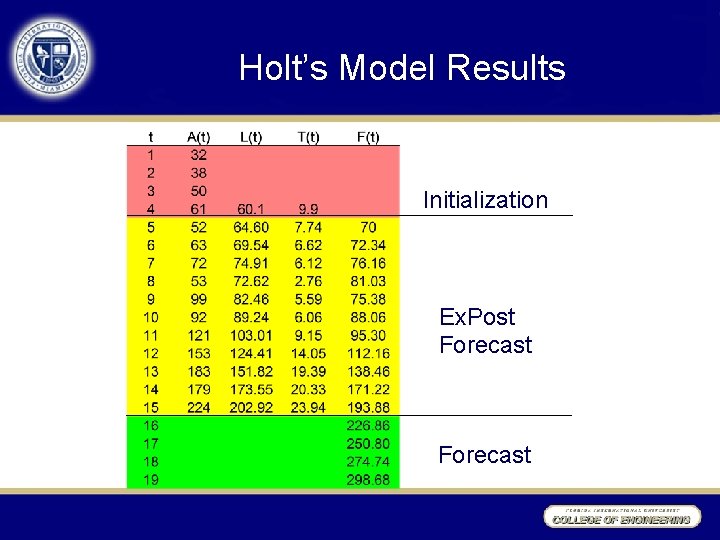
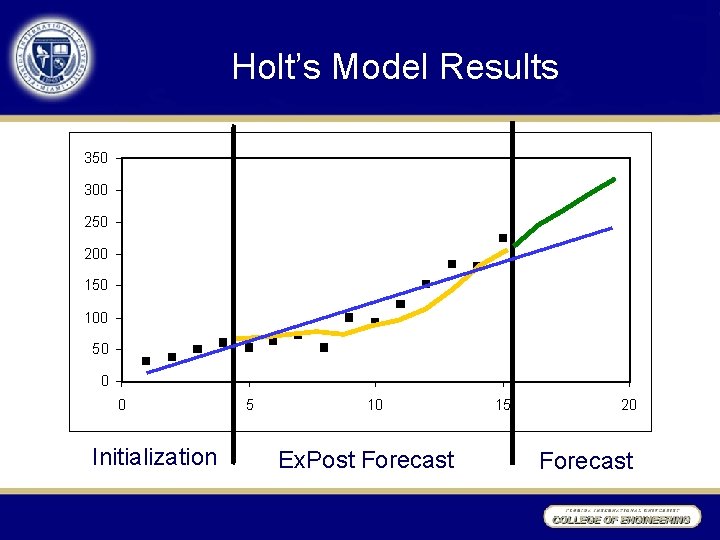
Holt’s Model Results Initialization Ex. Post Forecast

Holt’s Model Results 350 300 250 200 150 100 Regression 50 0 0 Initialization 5 10 Ex. Post Forecast 15 20 Forecast

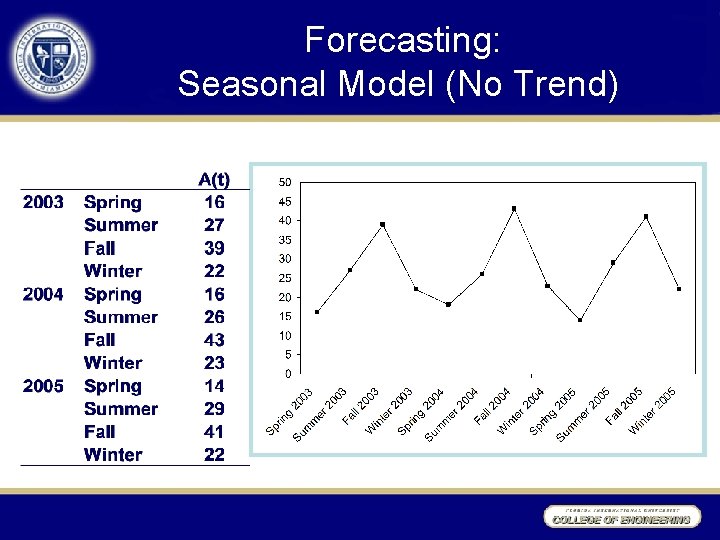
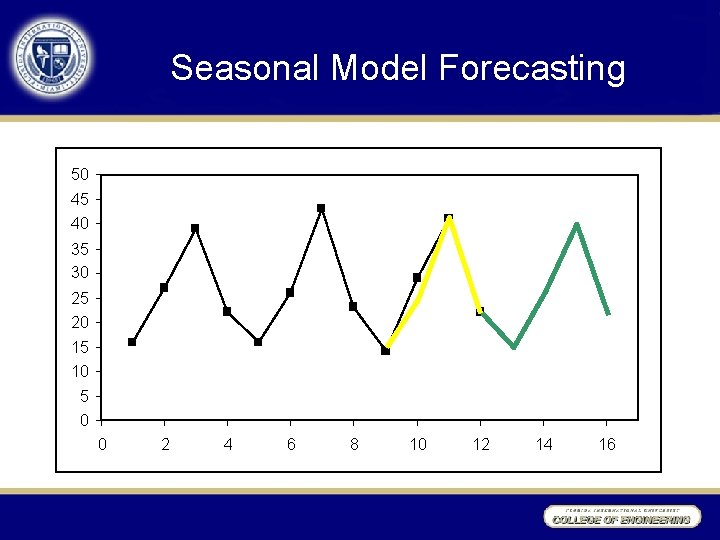
Forecasting: Seasonal Model (No Trend)

Seasonal Model Formulas L(t) = A(t) / S(t-p) + (1 - ) L(t-1) S(t) = g [A(t) / L(t)] + (1 - g) S(t-p) F(t+1) = L(t) * S(t+1 -p) p is the number of periods in a season Quarterly data: p = 4 Monthly data: p = 12

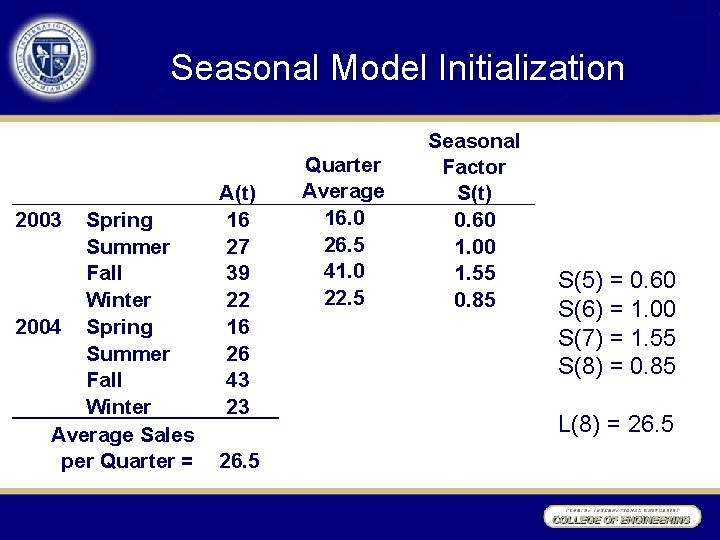
Seasonal Model Initialization 2003 Spring Summer Fall Winter 2004 Spring Summer Fall Winter Average Sales per Quarter = A(t) 16 27 39 22 16 26 43 23 26. 5 Quarter Average 16. 0 26. 5 41. 0 22. 5 Seasonal Factor S(t) 0. 60 1. 00 1. 55 0. 85 S(5) = 0. 60 S(6) = 1. 00 S(7) = 1. 55 S(8) = 0. 85 L(8) = 26. 5

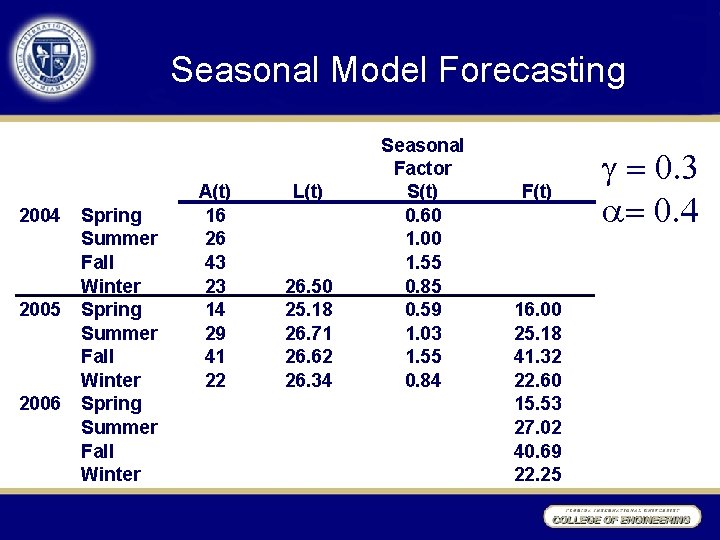
Seasonal Model Forecasting 2004 2005 2006 Spring Summer Fall Winter A(t) 16 26 43 23 14 29 41 22 L(t) 26. 50 25. 18 26. 71 26. 62 26. 34 Seasonal Factor S(t) 0. 60 1. 00 1. 55 0. 85 0. 59 1. 03 1. 55 0. 84 F(t) 16. 00 25. 18 41. 32 22. 60 15. 53 27. 02 40. 69 22. 25 g = 0. 3 = 0. 4

Seasonal Model Forecasting 50 45 40 35 30 25 20 15 10 5 0 0 2 4 6 8 10 12 14 16

Forecasting: Winter’s Model for Data with Trend and Seasonal Components L(t) = A(t) / S(t-p) + (1 - )[L(t-1)+T(t-1)] T(t) = [L(t) - L(t-1)] + (1 - ) T(t-1) S(t) = g [A(t) / L(t)] + (1 - g) S(t-p) F(t+1) = [L(t) + T(t)] S(t+1 -p)

Seasonal-Trend Model Decomposition • To initialize Winter’s Model, we will use Decomposition Forecasting, which itself can be used to make forecasts.

Decomposition Forecasting • There are two ways to decompose forecast data with trend and seasonal components: – Use regression to get the trend, use the trend line to get seasonal factors – Use averaging to get seasonal factors, “deseasonalize” the data, then use regression to get the trend. 41

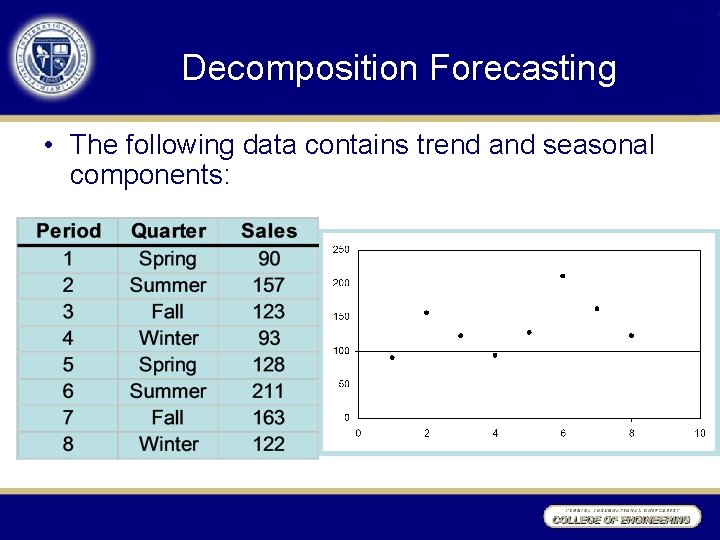
Decomposition Forecasting • The following data contains trend and seasonal components:

Decomposition Forecasting • The seasonal factors are obtained by the same method used for the Seasonal Model forecast: Period 1 2 3 4 5 6 7 8 Quarter Spring Summer Fall Winter Average = Sales 90 157 123 93 128 211 163 122 135. 9 Qtr. Ave. 109 184 143 107. 5 Seas. Factor 0. 80 1. 35 1. 05 0. 79 1. 00 Average to 1

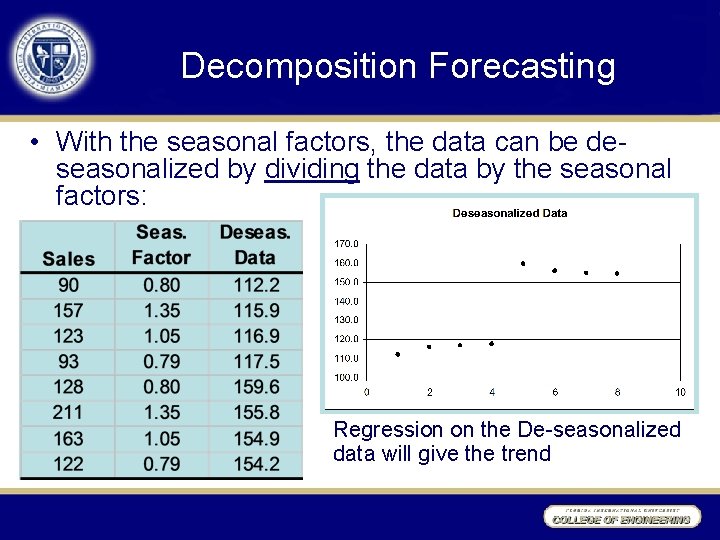
Decomposition Forecasting • With the seasonal factors, the data can be deseasonalized by dividing the data by the seasonal factors: Regression on the De-seasonalized data will give the trend

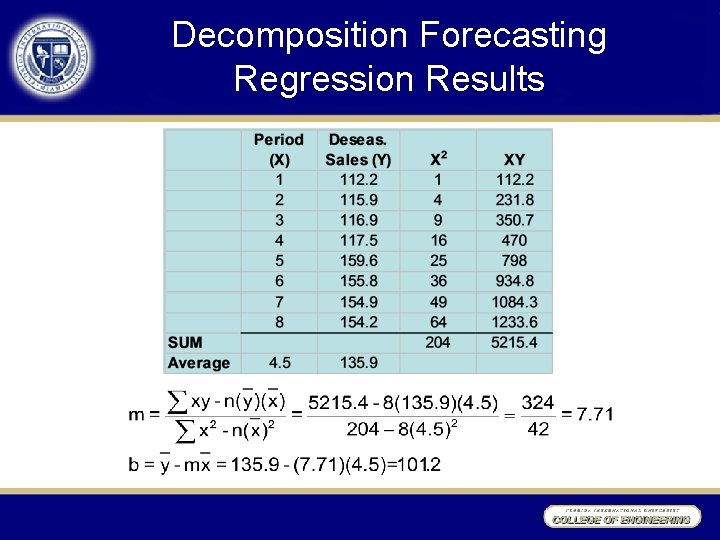
Decomposition Forecasting Regression Results

Decomposition Forecast • Regression on the de-seasonalized data produces the following results: – Slope (m) = 7. 71 – Intercept (b) = 101. 2 • Forecasts can be performed using the following equation – [mx + b](seasonal factor)

Decomposition Forecasting 300 250 200 150 100 50 0 1 2 3 4 5 6 7 8 9 10 11 12

Winter’s Model Initialization • We can use the decomposition forecast to define the following Winter’s Model parameters: L(n) = b + m (n) T(n) = m S(j) = S(j-p) So from our previous model, we have L(8) = 101. 2 + 8 (7. 71) = 162. 88 T(8) = 7. 71 S(5) = 0. 80 S(6) = 1. 35 S(7) = 1. 05 S(8) = 0. 79

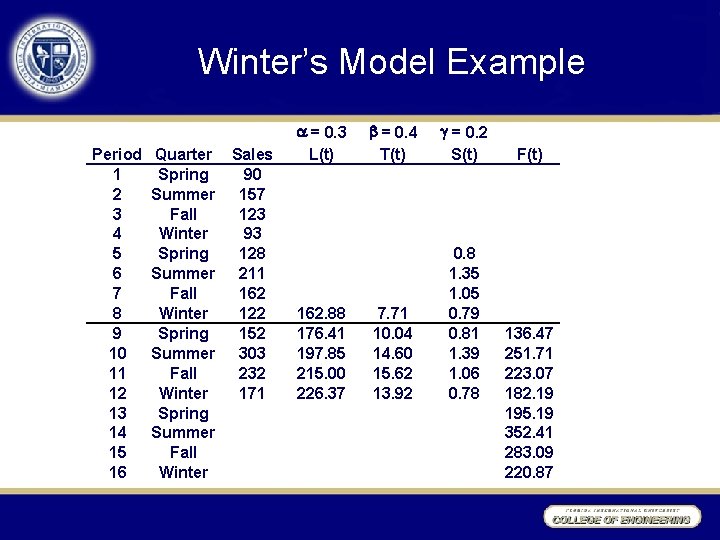
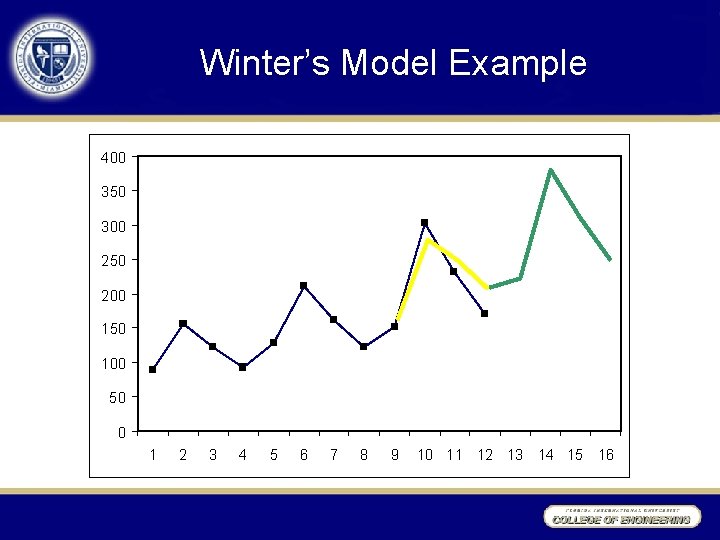
Winter’s Model Example Period 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Quarter Spring Summer Fall Winter Sales 90 157 123 93 128 211 162 122 152 303 232 171 a = 0. 3 L(t) 162. 88 176. 41 197. 85 215. 00 226. 37 b = 0. 4 T(t) g = 0. 2 S(t) 7. 71 10. 04 14. 60 15. 62 13. 92 0. 8 1. 35 1. 05 0. 79 0. 81 1. 39 1. 06 0. 78 F(t) 136. 47 251. 71 223. 07 182. 19 195. 19 352. 41 283. 09 220. 87

Winter’s Model Example 400 350 300 250 200 150 100 50 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Evaluating Forecasts “Trust, but Verify” Ronald W. Reagan • Computer software gives us the ability to mess up more data on a greater scale more efficiently • While software like SAP can automatically select models and model parameters for a set of data, and usually does so correctly, when the data is important, a human should review the model results • One of the best tools is the human eye

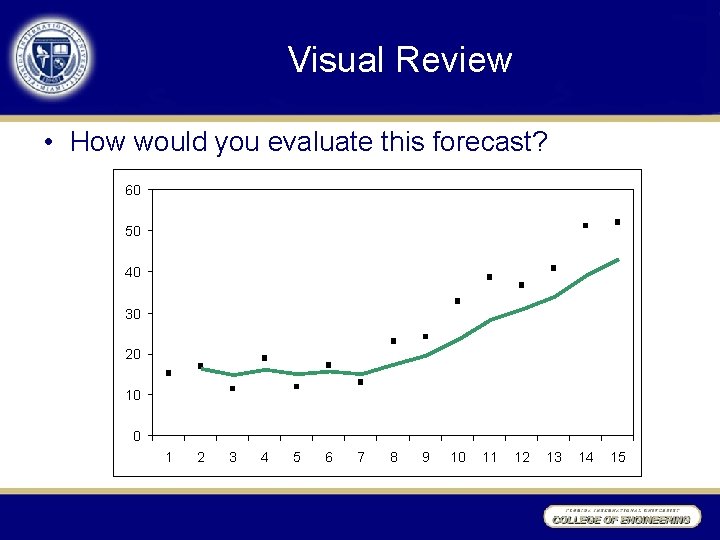
Visual Review • How would you evaluate this forecast? 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

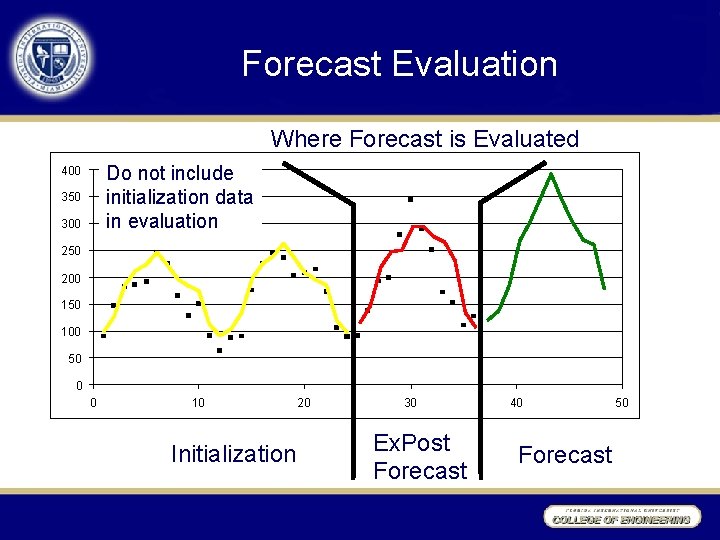
Forecast Evaluation Where Forecast is Evaluated Do not include initialization data in evaluation 400 350 300 250 200 150 100 50 0 0 10 Initialization 20 30 Ex. Post Forecast 40 Forecast 50

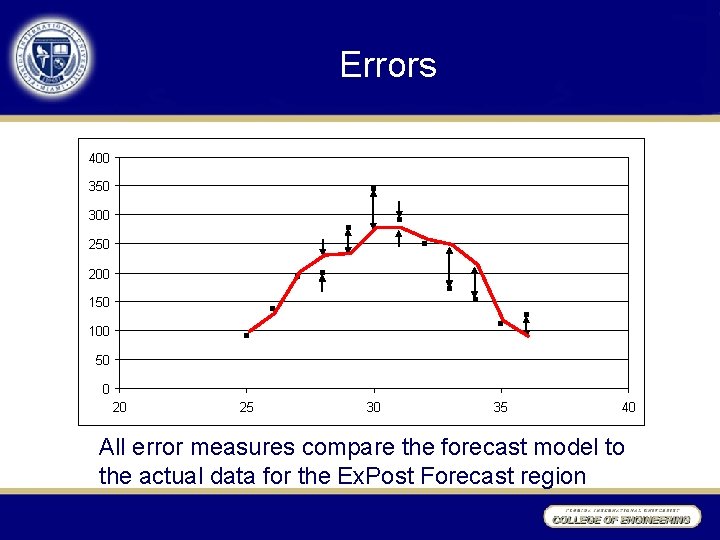
Errors 400 350 300 250 200 150 100 50 0 20 25 30 35 40 All error measures compare the forecast model to the actual data for the Ex. Post Forecast region

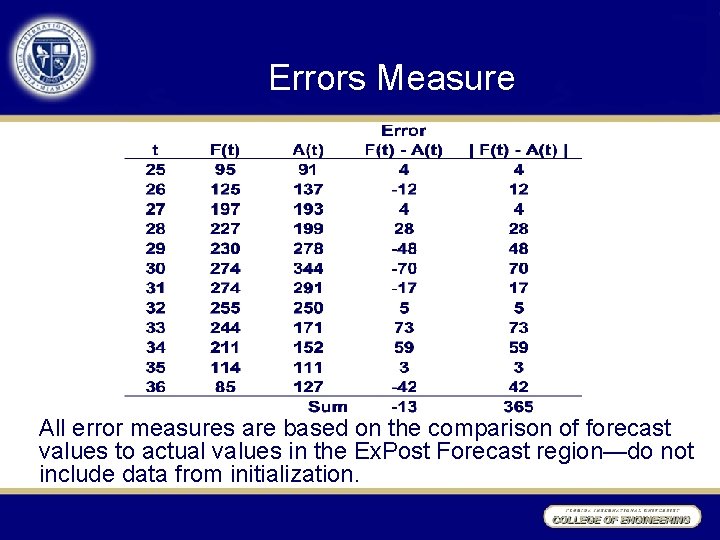
Errors Measure All error measures are based on the comparison of forecast values to actual values in the Ex. Post Forecast region—do not include data from initialization.

Bias and MAD

Bias and MAD • Bias tells us whether we have a tendency to overor under-forecast. If our forecasts are “in the middle” of the data, then the errors should be equally positive and negative, and should sum to 0. • MAD (Mean Absolute Deviation) is the average error, ignoring whether the error is positive or negative. • Errors are bad, and the closer to zero an error is, the better the forecast is likely to be. • Error measures tell how well the method worked in the Ex. Post forecast region. How well the forecast will work in the future is uncertain.

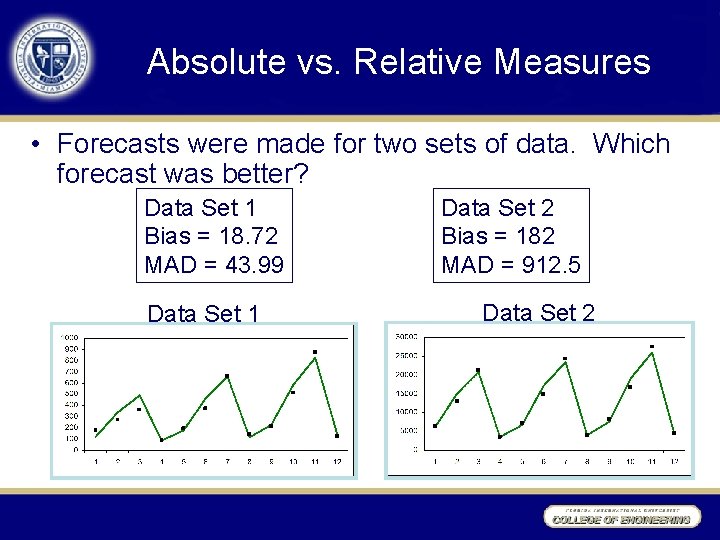
Absolute vs. Relative Measures • Forecasts were made for two sets of data. Which forecast was better? Data Set 1 Bias = 18. 72 MAD = 43. 99 Data Set 1 Data Set 2 Bias = 182 MAD = 912. 5 Data Set 2

MPE and MAPE • When the numbers in a data set are larger in magnitude, then the error measures are likely to be large as well, even though the fit might not be as “good”. • Mean Percentage Error (MPE) and Mean Absolute Percentage Error (MAPE) are relative forms of the Bias and MAD, respectively. • MPE and MAPE can be used to compare forecasts for different sets of data.

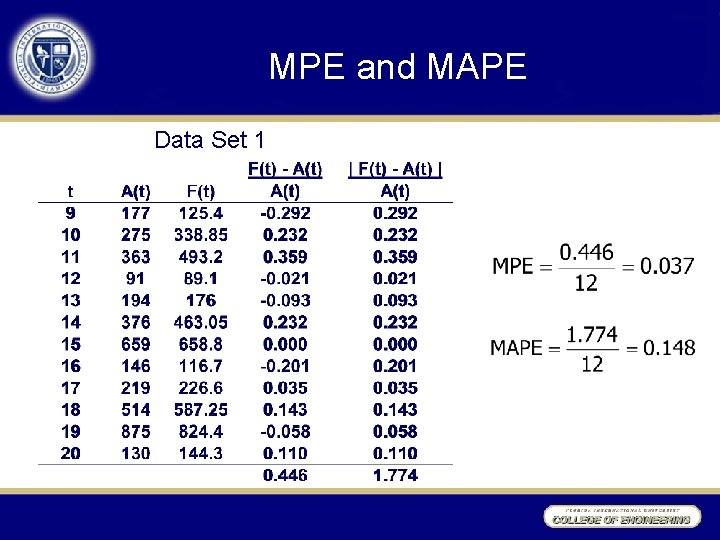
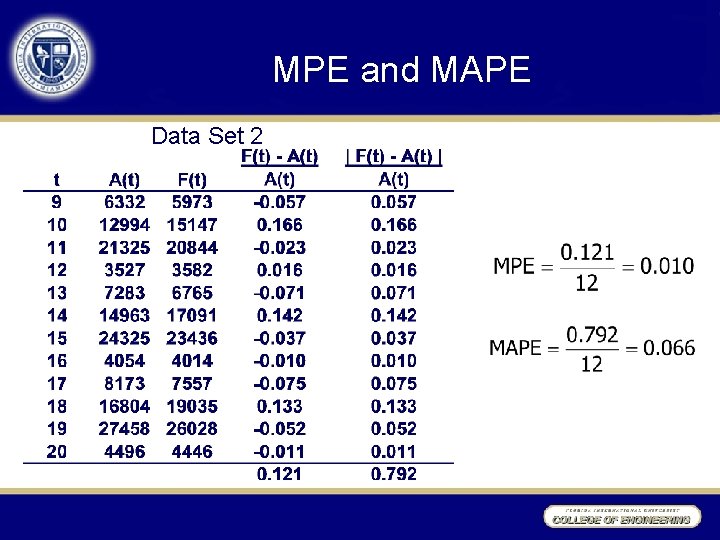
MPE and MAPE • Mean Percentage Error (MPE) • Mean Absolute Percentage Error (MAPE)

MPE and MAPE Data Set 1

MPE and MAPE Data Set 2

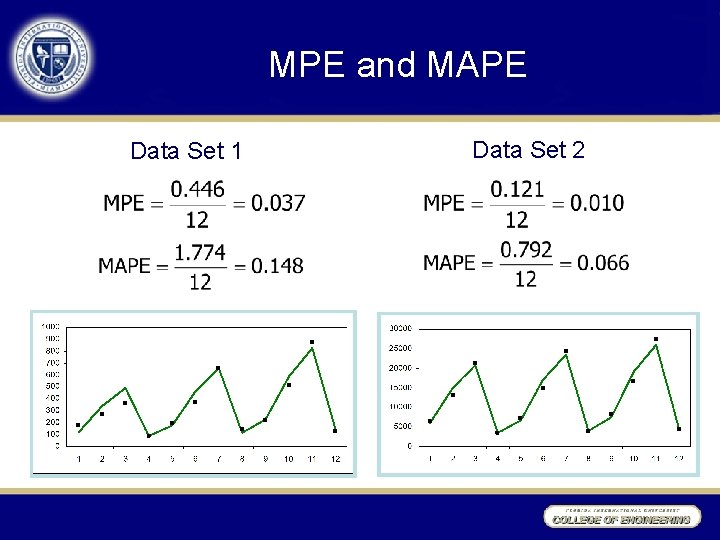
MPE and MAPE Data Set 1 Data Set 2

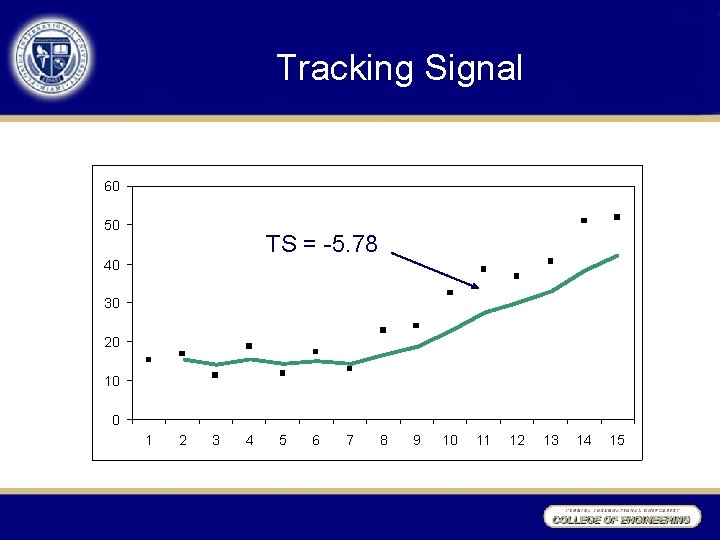
Tracking Signal • What’s happened in this situation? How could we detect this in an automatic forecasting environment? 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

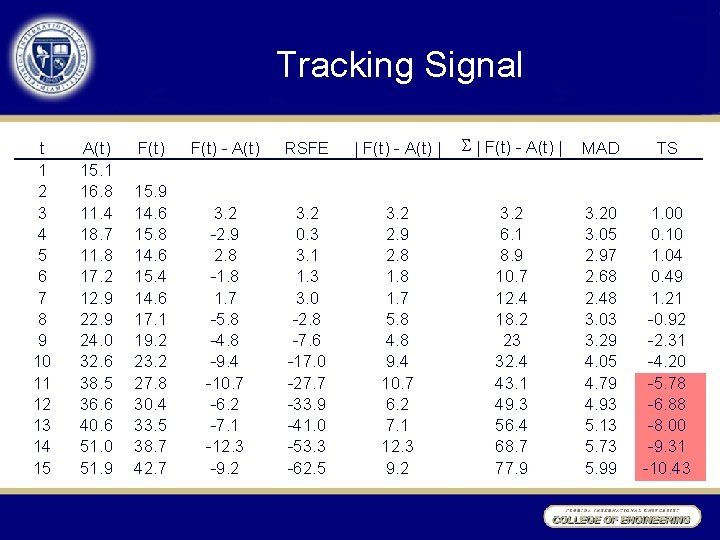
Tracking Signal • The tracking signal can be calculated after each actual sales value is recorded. The tracking signal is calculated as: • The tracking signal is a relative measure, like MPE and MAPE, so it can be compared to a set value (typically 4 or 5) to identify when forecasting parameters and/or models need to be changed.

Tracking Signal t 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A(t) 15. 1 16. 8 11. 4 18. 7 11. 8 17. 2 12. 9 24. 0 32. 6 38. 5 36. 6 40. 6 51. 0 51. 9 F(t) - A(t) RSFE | F(t) - A(t) | S | F(t) - A(t) | MAD TS 15. 9 14. 6 15. 8 14. 6 15. 4 14. 6 17. 1 19. 2 23. 2 27. 8 30. 4 33. 5 38. 7 42. 7 3. 2 -2. 9 2. 8 -1. 8 1. 7 -5. 8 -4. 8 -9. 4 -10. 7 -6. 2 -7. 1 -12. 3 -9. 2 3. 2 0. 3 3. 1 1. 3 3. 0 -2. 8 -7. 6 -17. 0 -27. 7 -33. 9 -41. 0 -53. 3 -62. 5 3. 2 2. 9 2. 8 1. 7 5. 8 4. 8 9. 4 10. 7 6. 2 7. 1 12. 3 9. 2 3. 2 6. 1 8. 9 10. 7 12. 4 18. 2 23 32. 4 43. 1 49. 3 56. 4 68. 7 77. 9 3. 20 3. 05 2. 97 2. 68 2. 48 3. 03 3. 29 4. 05 4. 79 4. 93 5. 13 5. 73 5. 99 1. 00 0. 10 1. 04 0. 49 1. 21 -0. 92 -2. 31 -4. 20 -5. 78 -6. 88 -8. 00 -9. 31 -10. 43

Tracking Signal 60 50 TS = -5. 78 40 30 20 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15