Delayed feedback of sampled higher derivatives Tamas Insperger

Delayed feedback of sampled higher derivatives Tamas Insperger€, Gabor Stepan€, Janos Turi$ €Department of Applied Mechanics Budapest University of Technology and Economics $Programs in Mathematical Sciences University of Texas at Dallas

Contents - Stability gained with time-periodic parameters Human balancing (delay and threshold) The labyrinth and the eye – a mechanical view Robotic balancing (sampling and round-off) Micro-chaos (stable & unstable) Segway – without gyros Retarded, neutral and advanced FDEs (linear) Stability achieved with sampled higher derivatives Conclusions

The delayed Mathieu equation Analytically constructed stability chart for testing numerical methods and algorithms Time delay and time periodicity are equal: Mathieu equation (1868) Delayed oscillator (1941)
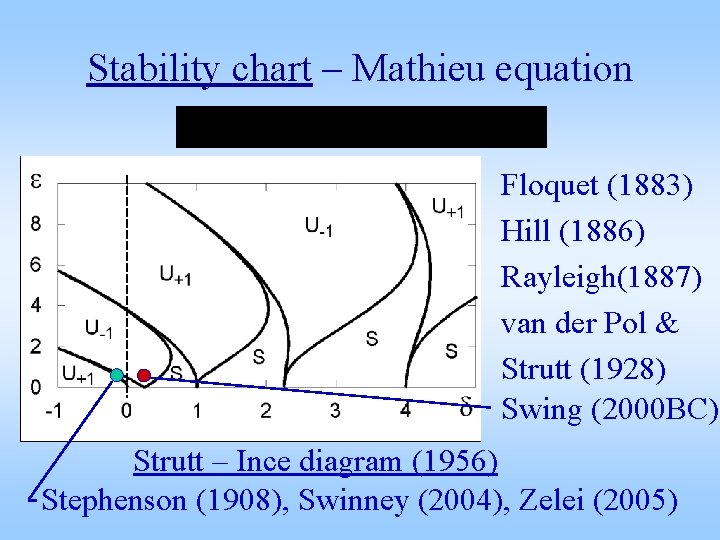
Stability chart – Mathieu equation Floquet (1883) Hill (1886) Rayleigh(1887) van der Pol & Strutt (1928) Swing (2000 BC) Strutt – Ince diagram (1956) Stephenson (1908), Swinney (2004), Zelei (2005)
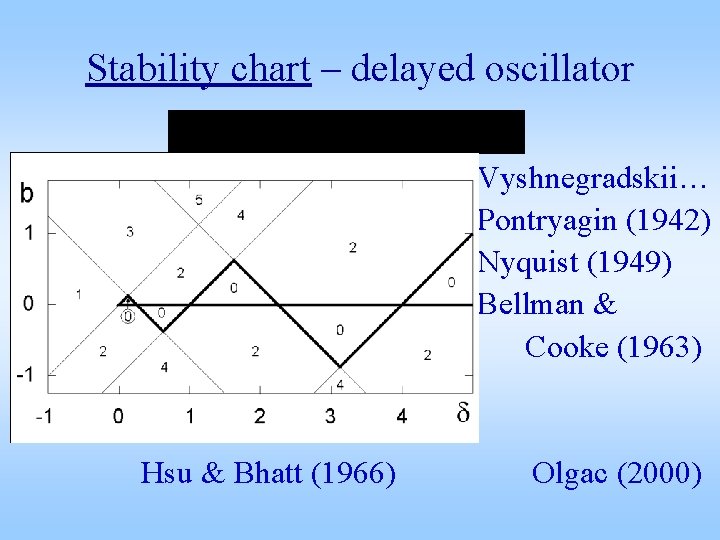
Stability chart – delayed oscillator Vyshnegradskii… Pontryagin (1942) Nyquist (1949) Bellman & Cooke (1963) Hsu & Bhatt (1966) Olgac (2000)
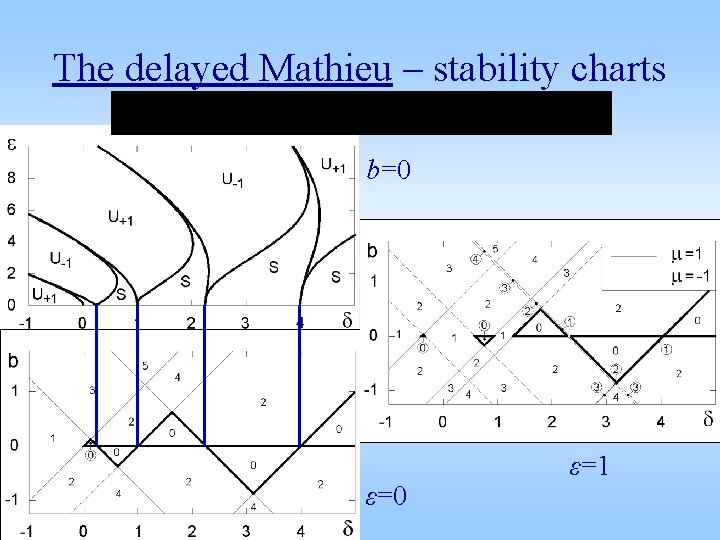
The delayed Mathieu – stability charts b=0 ε=1
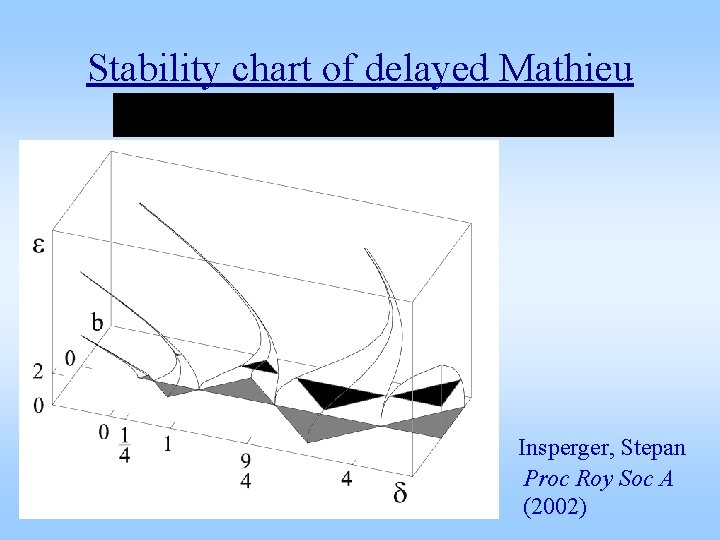
Stability chart of delayed Mathieu Insperger, Stepan Proc Roy Soc A (2002)

Chaos is amusing Unpredictable games – strong nonlinearities: throw dice, play cards/chess, computer games ball games (football, soccer, basketball… impact) plus nonlinear rules (tennis 6/4, 0/6, 6/4, snooker) balancing (skiing, skating, kayak, surfing, …) Ice-hockey (one of the most unpredictable games) - impacts between club/puck/wall - impacts between players/wall - self-balancing of players on ice (non-holonomic) - continuous and fast exchanging of players
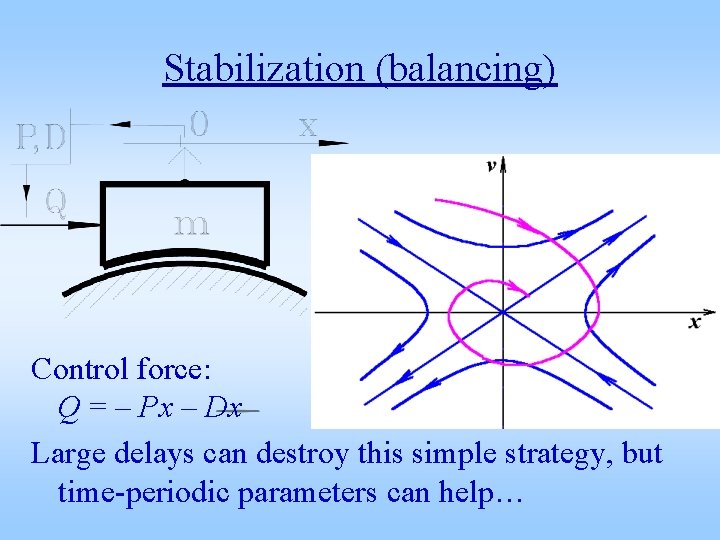
Stabilization (balancing) Control force: Q = – Px – Dx Large delays can destroy this simple strategy, but time-periodic parameters can help…

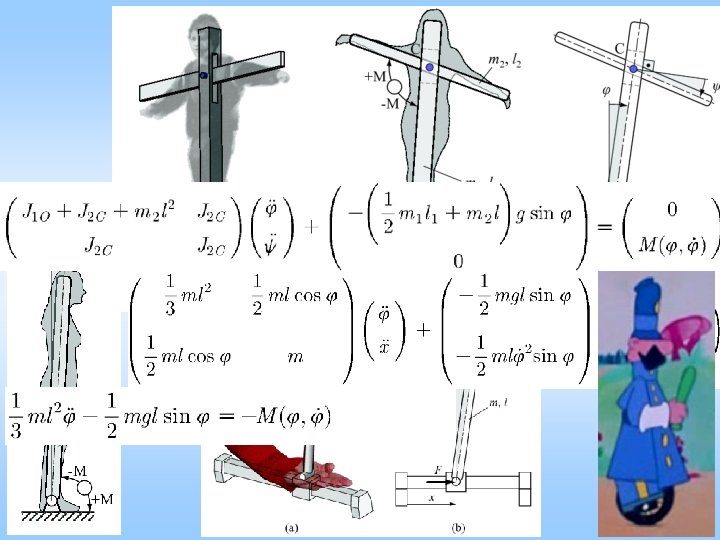
Balancing inverted pendulum Higdon, Cannon (1962) … 10 -20 papers / year n = 2 Do. F , x ; x – cyclic coordinate linearization at = 0

Human balancing Analogous or digital? Winking, eye-motion – ‘self-sampling’ plus neurons firing… still, not ‘digital’ 1) Q(t) = P (t) + D (t) (PD control) ≡ 0 is exponentially stable D > 0, P > mg 2) Q(t) = P (t – ) + D (t – ) (with ‘reflex’ delay )
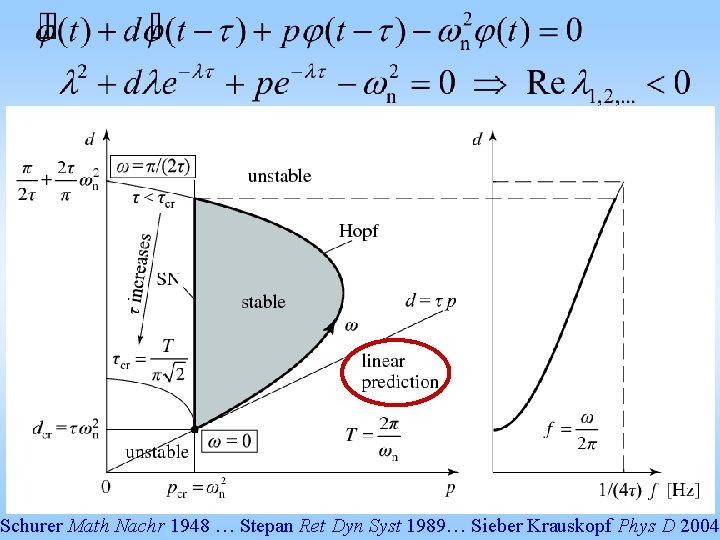
Schurer Math Nachr 1948 … Stepan Ret Dyn Syst 1989… Sieber Krauskopf Phys D 2004
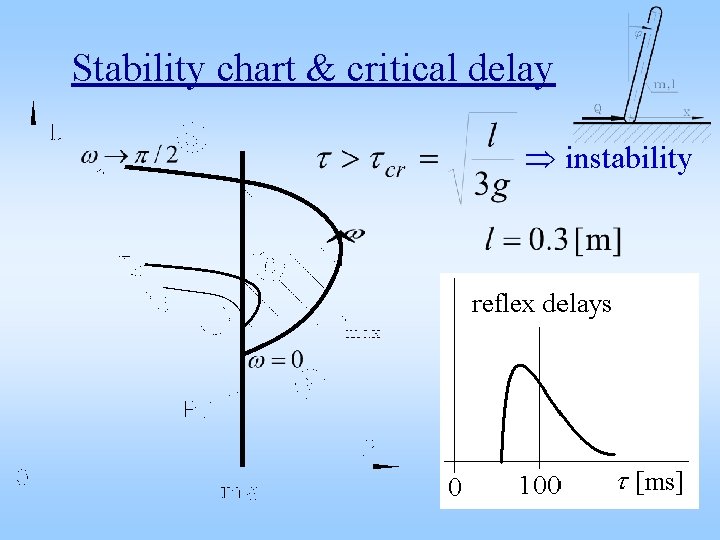
Stability chart & critical delay instability
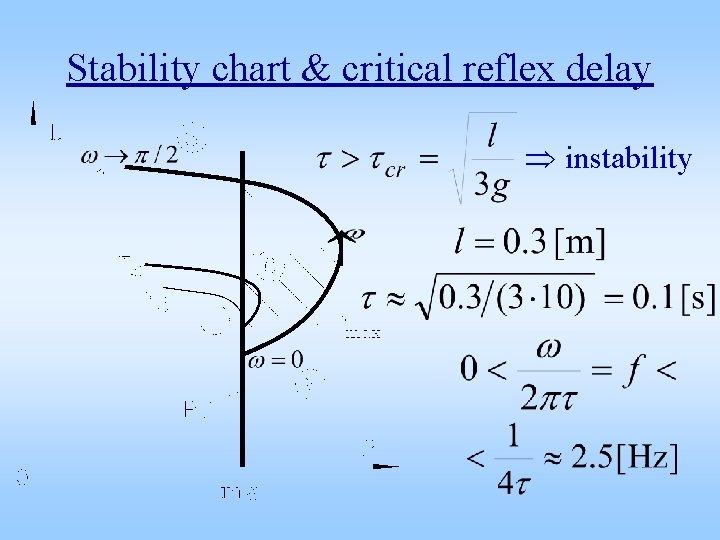
Stability chart & critical reflex delay instability
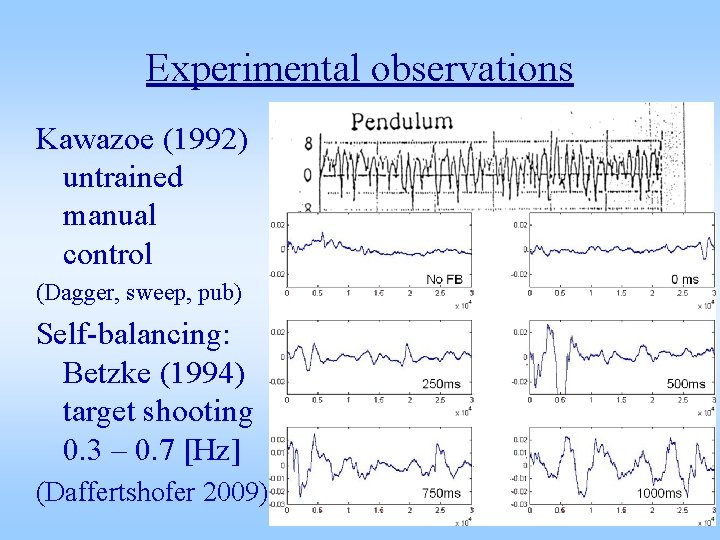
Experimental observations Kawazoe (1992) untrained manual control (Dagger, sweep, pub) Self-balancing: Betzke (1994) target shooting 0. 3 – 0. 7 [Hz] (Daffertshofer 2009)

Stability is the art of keeping the balance
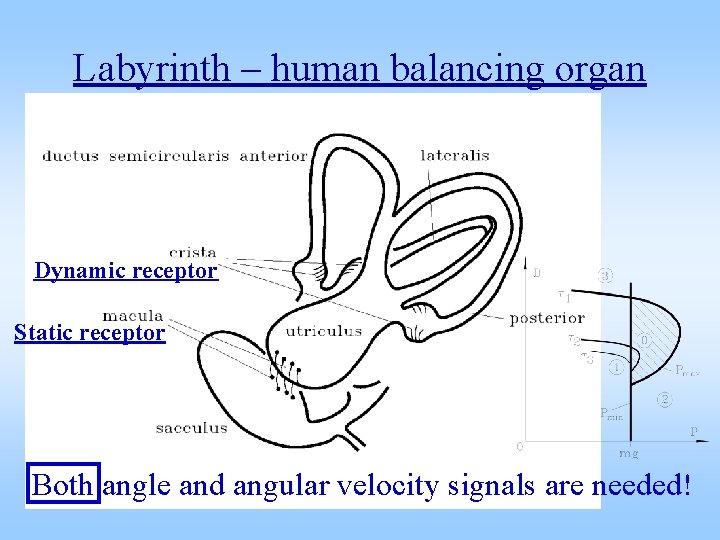
Labyrinth – human balancing organ Dynamic receptor Static receptor Both angle and angular velocity signals are needed!

Vision and balancing • Vision can help balancing even when labyrinth does not function properly (e. g. , ‘dry ear’ effect) • The visual system also provides the necessary angle and angular velocity signals! • But: the vertical direction is needed (buildings, trees), otherwise it fails… • Delay in vision and ‘thinking’
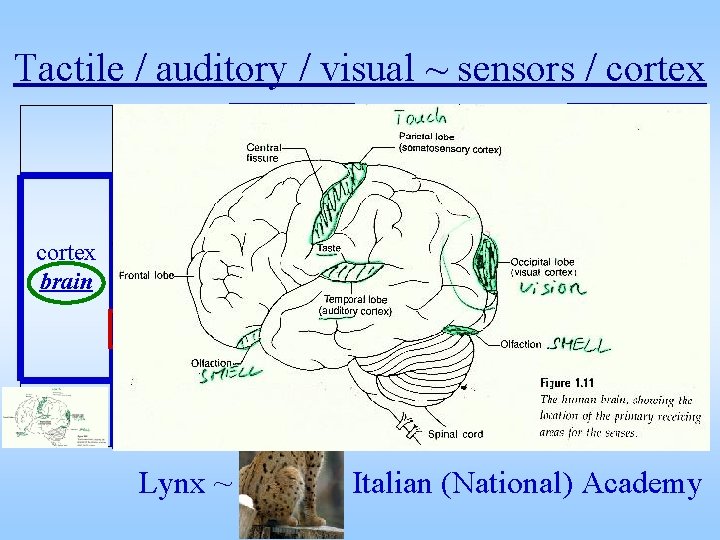
Tactile / auditory / visual ~ sensors / cortex organ overall performance effect small skin large small pressure cortex medium ear brain small medium object sound large small delay distance Lynx ~ small eye light fast medium slow large delay distance Italian (National) Academy
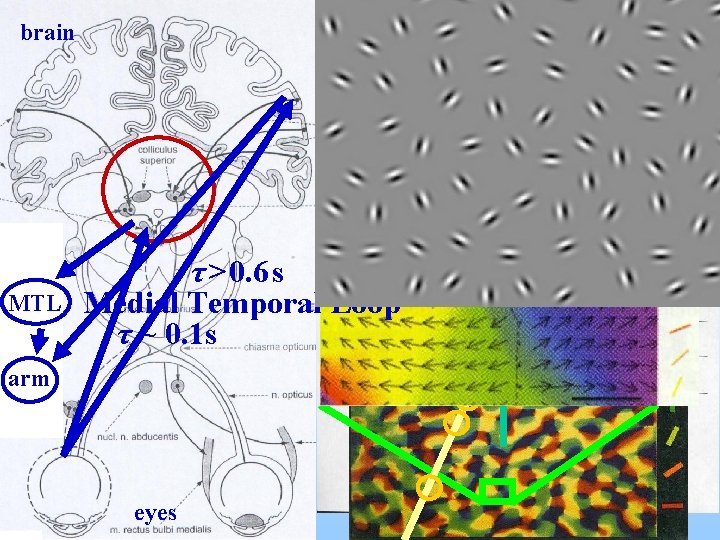
brain Colliculus superior MTL τ > 0. 6 s Medial Temporal Loop τ ~ 0. 1 s arm eyes

Human balancing – some conclusions We could reduce the delay below critical value through the MTL (Medial Temporal Loop) But we cannot reduce much the thresholds of our sensory system (glasses. . . ) Both delay and threshold increase with age – see increasing number of fall-overs in elderly homes Reduce gains, add stochastic perturbation to signal to decrease threshold at a 3 rd sensory system – our feet (Moss, Milton, Nature, 2003) Delay & threshold lead to chaos… (stochastic nature)

Digital balancing 1) Q = 0 – no control = 0 is unstable 2) Q(t) = P (t) + D (t) (PD control) = 0 is exponentially stable D > 0, P > mg 3) Q(t) ≡ P (tj – ) + D (tj – ) (with sampling )
Alice’s Adventures in Wonderland Lewis Carroll (1899)
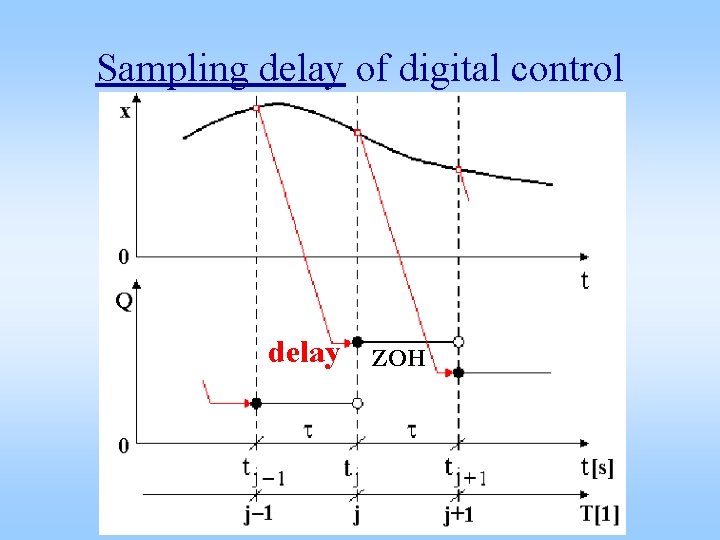
Sampling delay of digital control delay ZOH

Digitally controlled pendulum , (Claussen)

Stability of digital control – sampling Hopf pitchfork



ABB Sampling frequency of industrial robots ~ 30 Hz for the years 1990 – 2005 above 100 Hz recently Force control (EU 6 FP Reha. Rob project), and balancing (stabilization-)tasks Reha. Rob Balancing
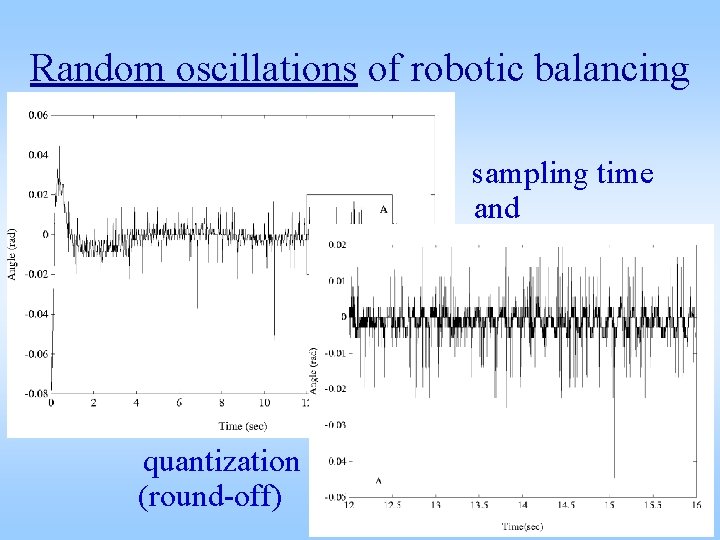
Random oscillations of robotic balancing sampling time and quantization (round-off)

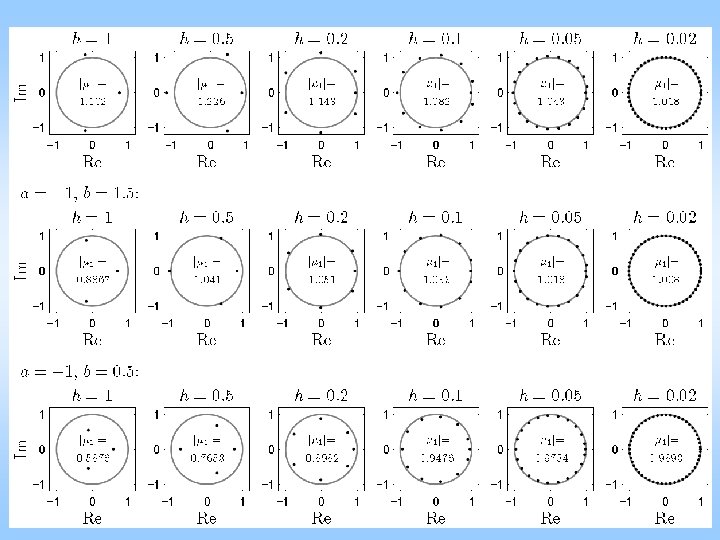
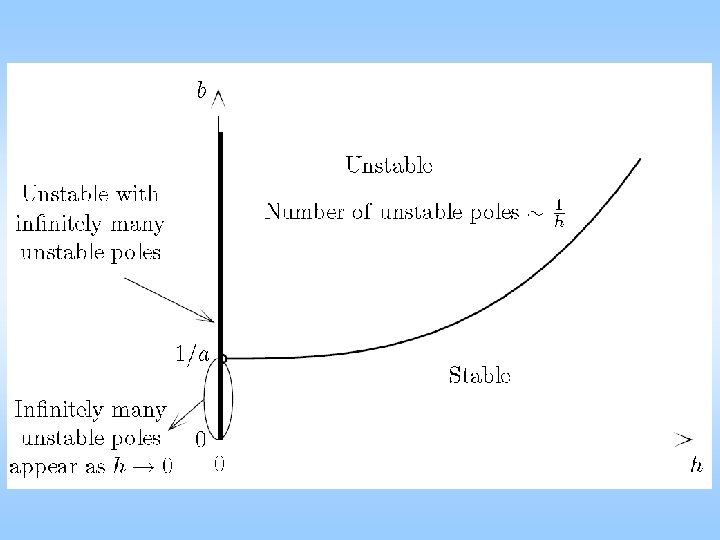
Stability of digital control – round-off h – one digit converted to control force det( I – B) = 0 1 = e >1, 2 = e– , 3 = 0

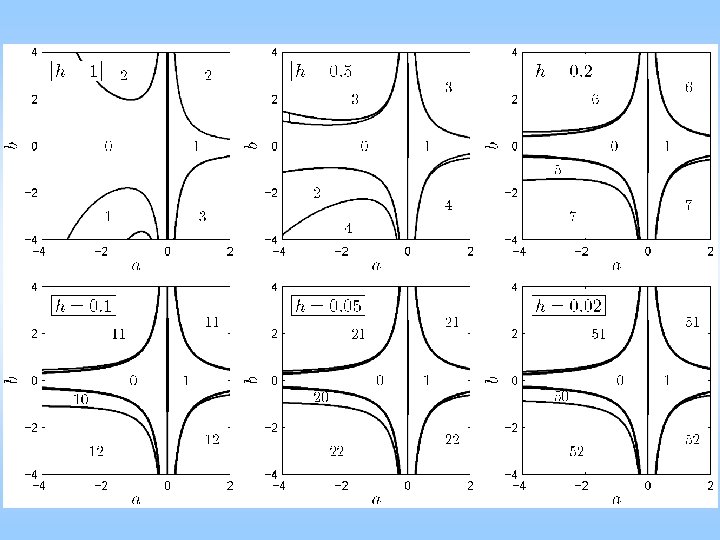
1 D cartoon – the micro-chaos map Drop 2 dimensions, rescale x with h a e , b P A pure math approach ( p > 0 , p < q ) solution with xj = y(j) leads to -chaos map, a = ep, b = q(ep – 1)/p a > 1, (0 <) a – b < 1 small scale: xj+1= a xj , large scale: xj+1= (a – b) xj
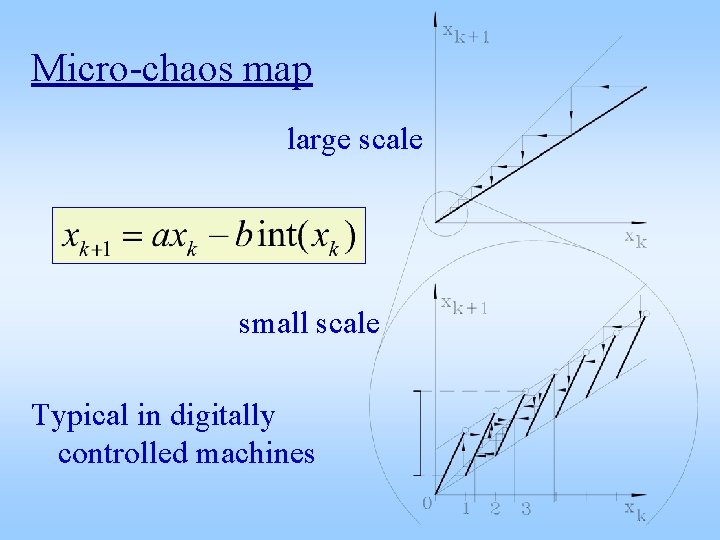
Micro-chaos map large scale small scale Typical in digitally controlled machines

2 D micro-chaos map ZOH + delay, and round-off for 1 st order process: (p > 0, p < q) Solution and Poincare lead to (a >1, a – b < 1) Linearization at fixed points leads to eigenvalues So in 1 step the solution settles at an attractor that has a graph similar to the 1 D micro-chaos map Csernak, Stepan (Int J Bif Chaos ’ 09)

3 D micro-chaos Enikov, Stepan (J Vib Cont, 98)


Vertical direction?




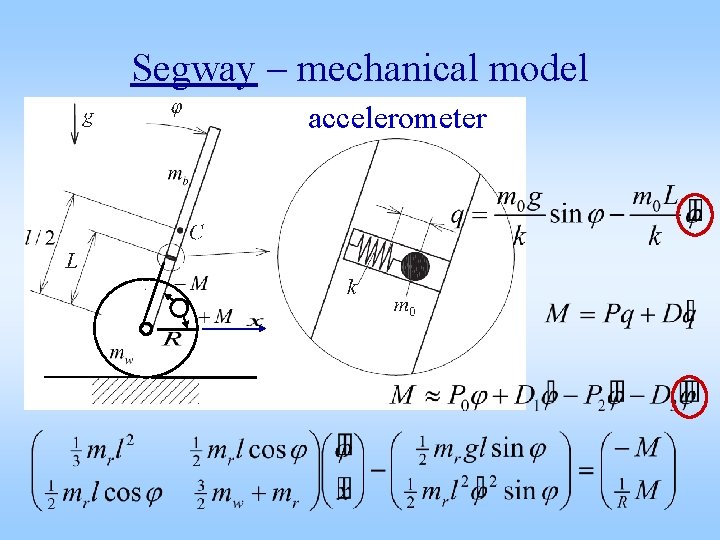
Segway – mechanical model accelerometer

Segway control with delay Analog case Advance DDE …unstable for any “time delay”. Digital case

Retarded DDE Analog (Hayes, 1951) Digital
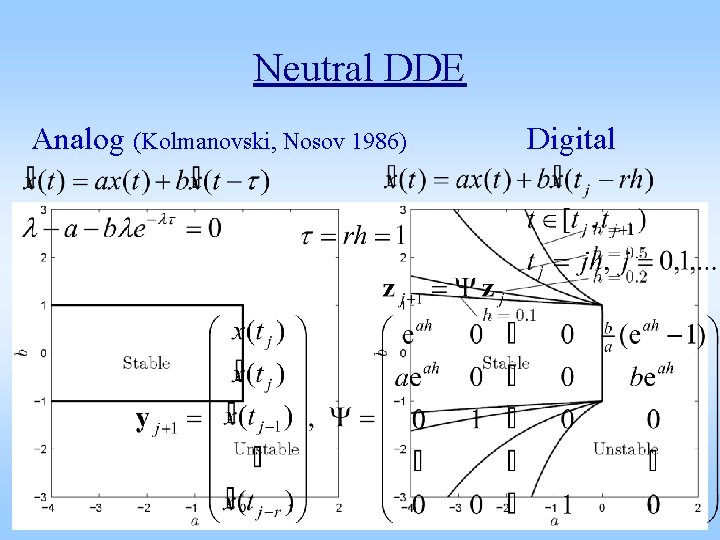
Neutral DDE Analog (Kolmanovski, Nosov 1986) Digital

Advanced DDE Analog (El’sgolt’c 1964) Digital

Balancing the self-balanced Warning: only fathers have the right to do this… kid Thank you for your attention! Delay effects in brain dynamics Phil. Trans. R. Soc. A 367 (2009) doi: 10. 1098/rsta. 2008. 0279
- Slides: 52