Delaunay Triangulations for 3 D Mesh Generation ShangHua

Delaunay Triangulations for 3 D Mesh Generation Shang-Hua Teng Department of Computer Science, UIUC Work with: Gary Miller, Dafna Talmor, Noel Walkington Siu-Wing Cheng, Tamal Dey, Herbert Edelsbrunner, Micheal Facello Xiang-Yang Li and Alper Üngör

Unstructured Meshes

Numerical Methods Formulation Math+Engineering Mesh Generation geometric structures Approximation Numerical Analysis Linear System algorithm data structures Domain, Boundary, and PDEs Point Set: Triangulation: Finite ad hoc octree Delaunay element difference volume Ax=b direct method multigrid iterative method

Outline n Mesh Generation in 2 D u Mesh Qualities u Meshing Methods u Meshes and Circle Packings n Mesh Generation in 3 D u Slivers u Numerical Solution: Control Volume Method u Geometric Solution: Sliver Removal by Weighted Delaunay Triangulations

Badly Shaped Triangles

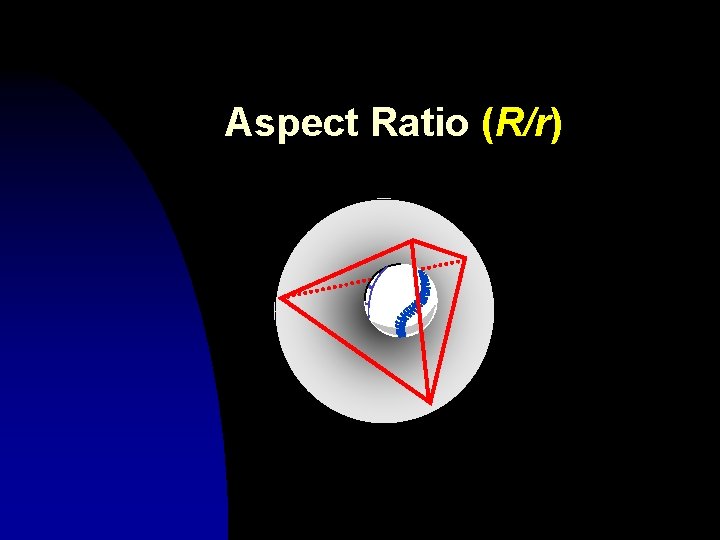
Aspect Ratio (R/r)

Meshing Methods The goal of a meshing algorithm is to generate a well-shaped mesh that is as small as possible. n n n Advancing Front Quadtree and Octree Refinement Delaunay Based u Delaunay Refinement u Sphere Packing u Weighted Delaunay Triangulation

Balanced Quadtree Refinements (Bern-Eppstein-Gilbert)

Quadtree Mesh

Delaunay Triangulations

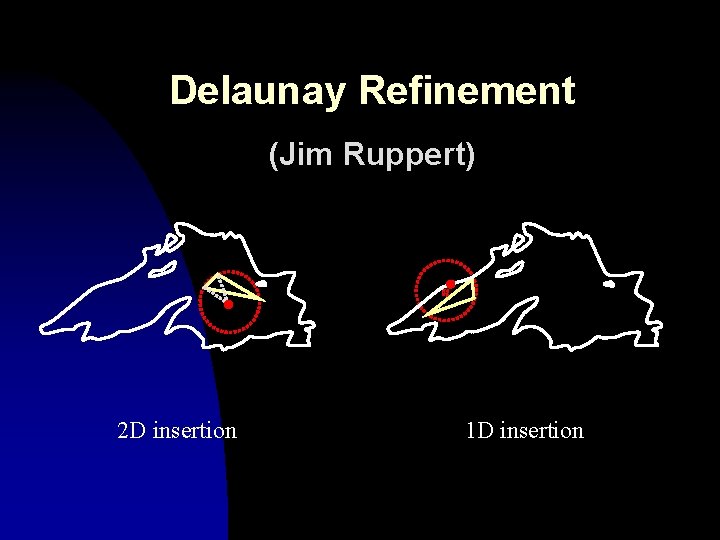
Why Delaunay? n n n Maximizes the smallest angle in 2 D. Has efficient algorithms and data structures. Delaunay refinement: u In 2 D, it generates optimal size, natural looking meshes with 20. 7 o (Jim Ruppert)

Delaunay Refinement (Jim Ruppert) 2 D insertion 1 D insertion

Delaunay Mesh

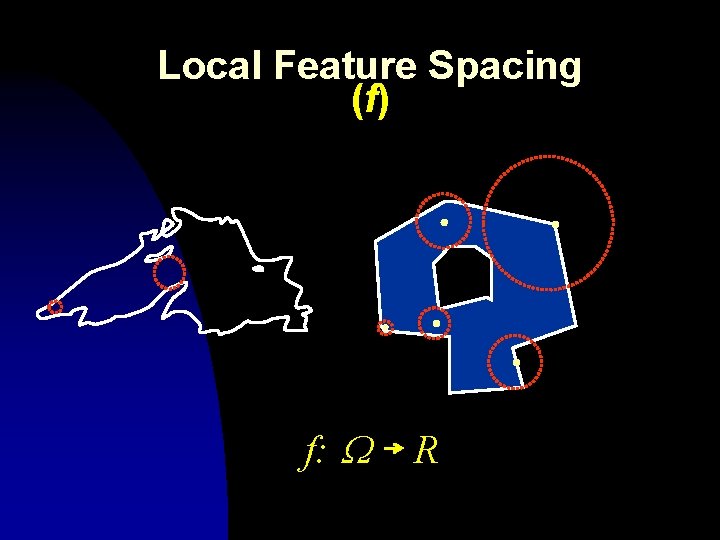
Local Feature Spacing (f) f: W R

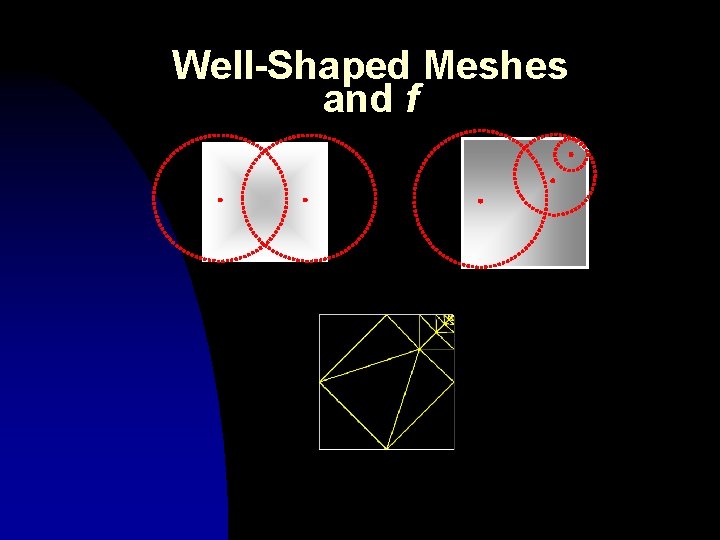
Well-Shaped Meshes and f

f is 1 -Lipschitz and Optimal

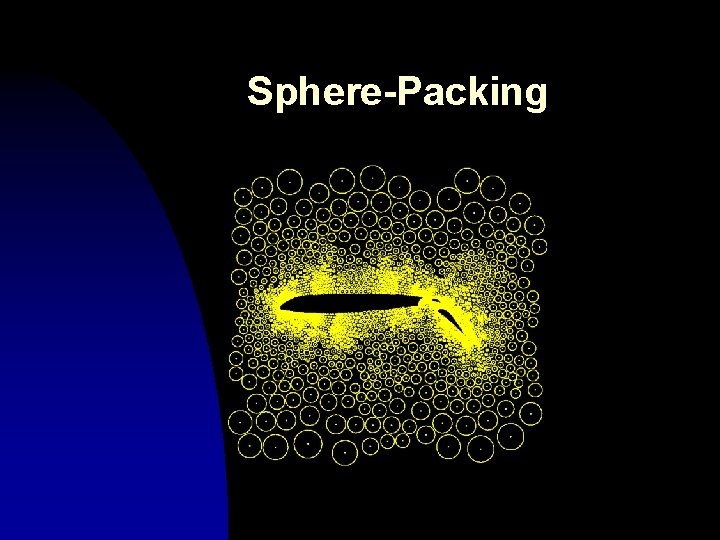
Sphere-Packing

b -Packing a Function f f(p)/2 p q n No large empty gap: the radius of the largest empty sphere passing q is at most b f(q).

The Packing Lemma (2 D) (Miller-Talmor-Teng. Walkington) n n The Delaunay triangulation of a b -packing is a well-shaped mesh of optimal size. Every well-shaped mesh defines a b -packing.

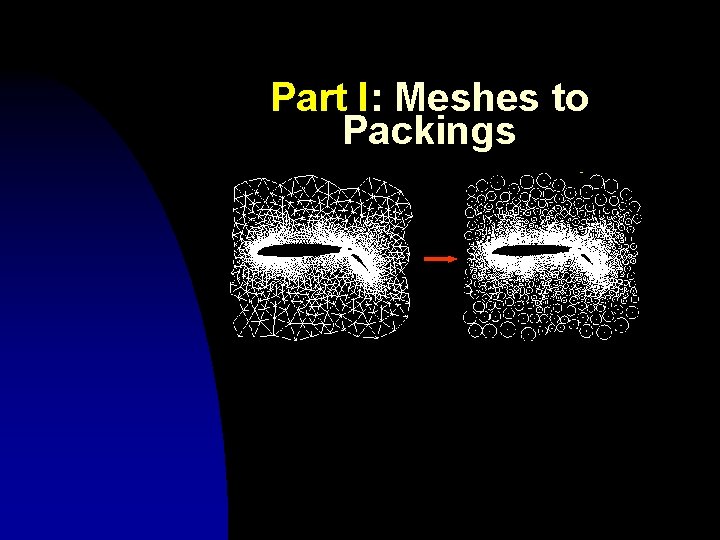
Part I: Meshes to Packings

Part II: Packings to Meshes

3 D Challenges n n Delaunay failed on aspect ratio Quadtree becomes octree (Mitchell -Vavasis) Meshes become much larger Research is more interesting?

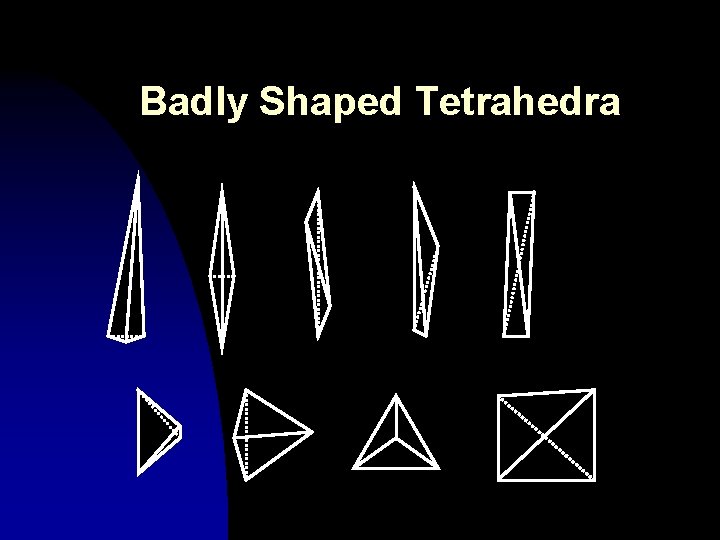
Badly Shaped Tetrahedra

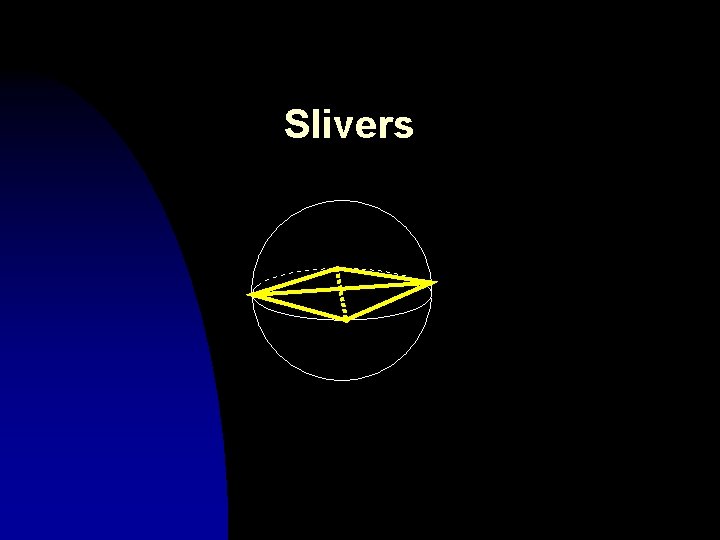
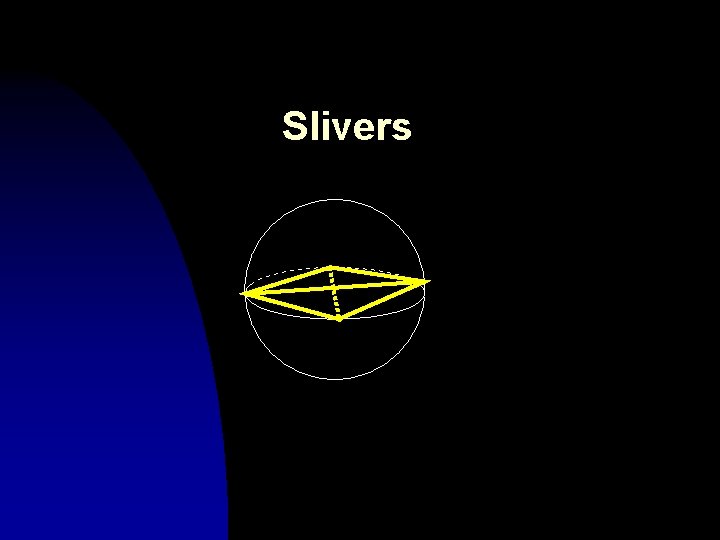
Slivers

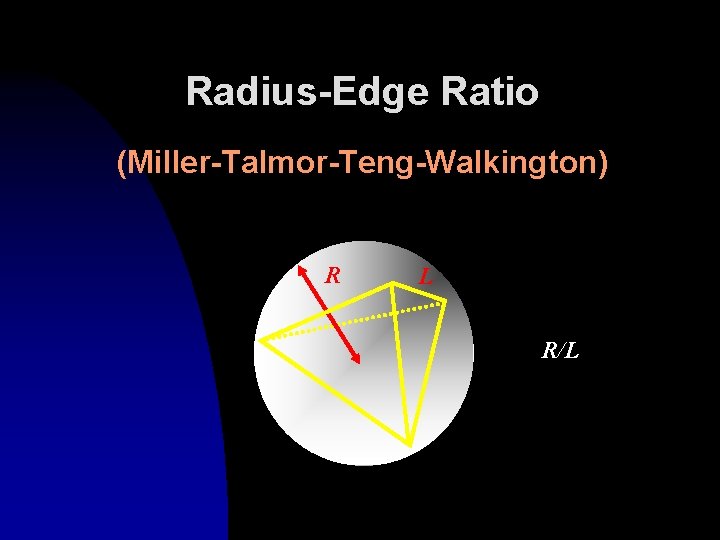
Radius-Edge Ratio (Miller-Talmor-Teng-Walkington) R L R/L

The Packing Lemma (3 D) (Miller-Talmor-Teng. Walkington) n n The Delaunay Triangulation of a b -packing is a well-shaped mesh (using radius-edge ratio) of optimal size. Every well-shaped (aspect-ratio or radiusedge ratio) mesh defines a b -packing.

Uniform Ball Packing n In any dimension, if P is a maximal packing of unit balls, then the Delaunay triangulation of P has radius-edge at most 1. ||e|| is at least 2 r r is at most 2

Constant Degree Lemma (3 D) (Miller-Talmor-Teng. Walkington) n The vertex degree of the Delaunay triangulation with a constant radius-edge ratio is bounded by a constant.

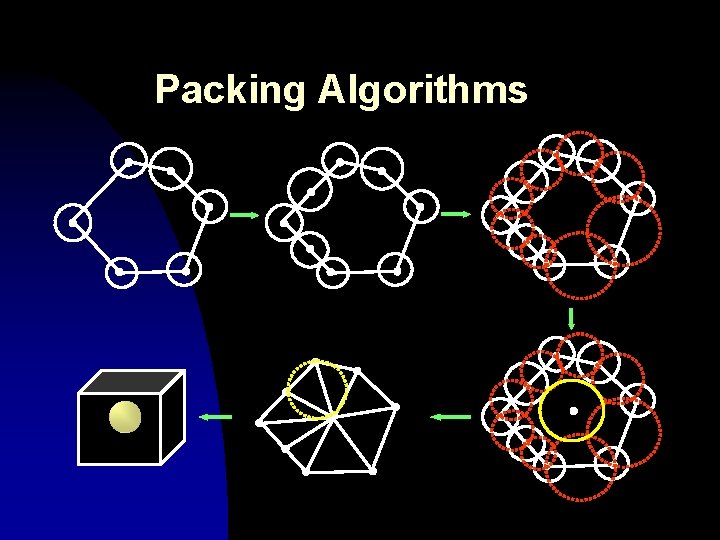
Packing Algorithms

Well-Spaced Points

Well-Spaced Points

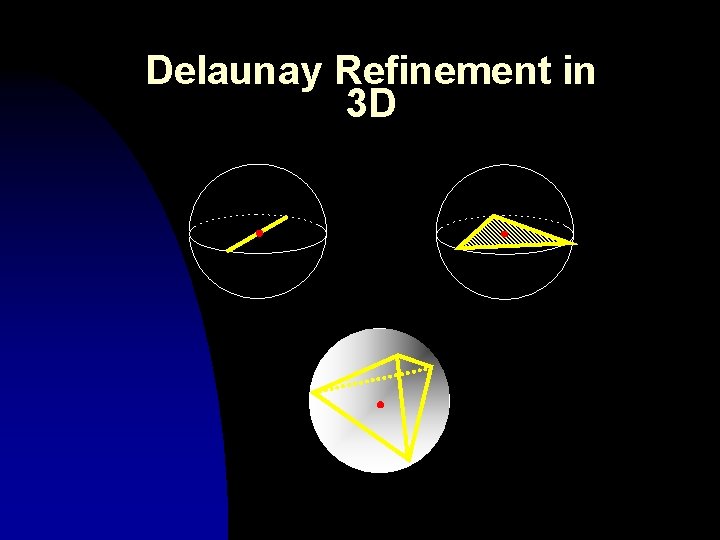
Packing in 3 D n n n Pack 2 D boundaries by quadtree approximation or Ruppert Refinement Approximate the LFS by octree Locally sample the region to create a well-spaced point set • 3 D Delaunay refinement also generates meshes with a good edge-radius ratio (Shewchuck)

Delaunay Refinement in 3 D

Slivers

Sliver: the geo-roach

Coping with Slivers: Control-Volume. Method (Miller-Talmor-Teng-Walkington)

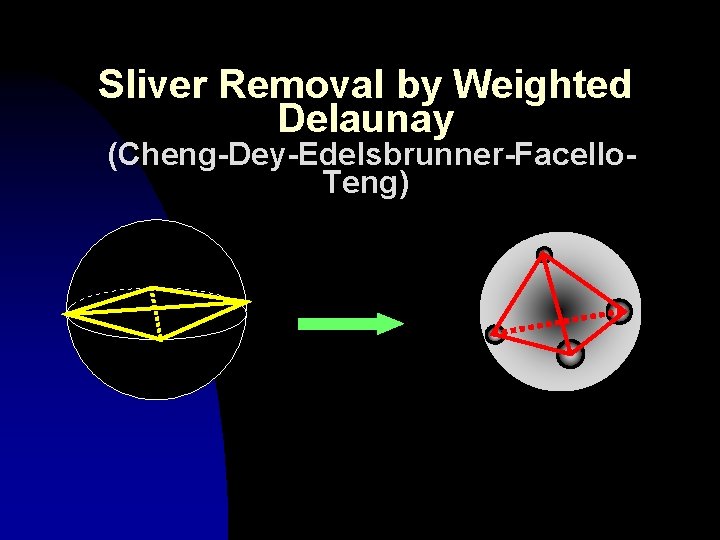
Sliver Removal by Weighted Delaunay (Cheng-Dey-Edelsbrunner-Facello. Teng)

Weighted Points and Distance p z

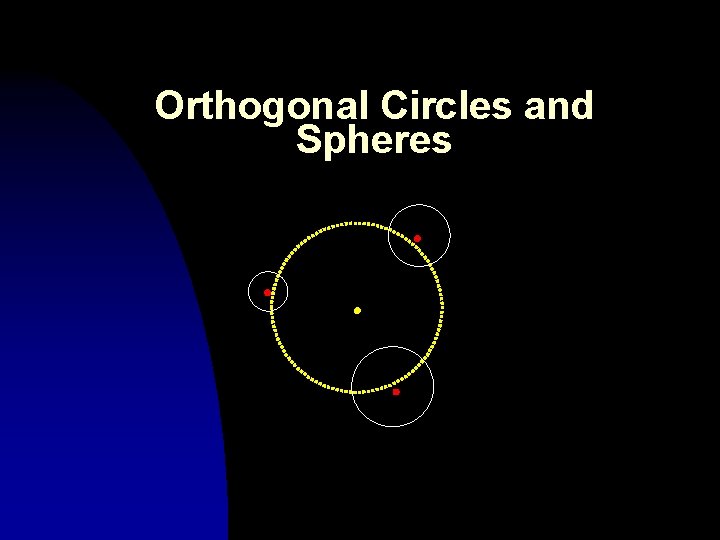
Orthogonal Circles and Spheres

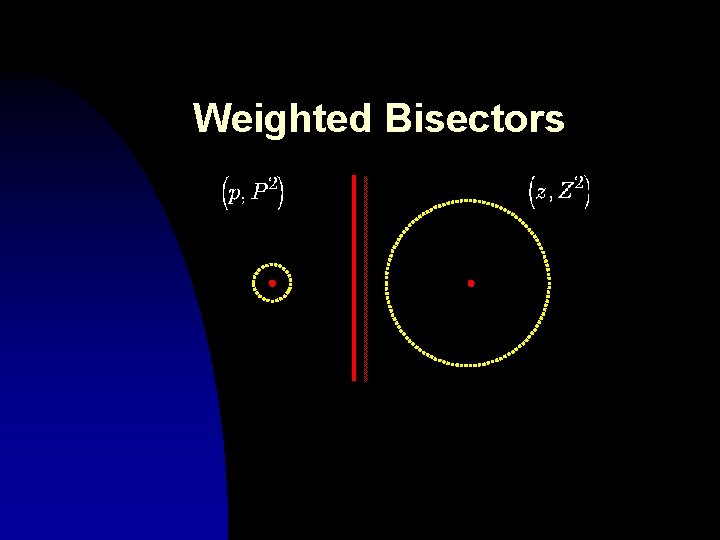
Weighted Bisectors

Weighted Delaunay

Weighted Delaunay and Convex Hull

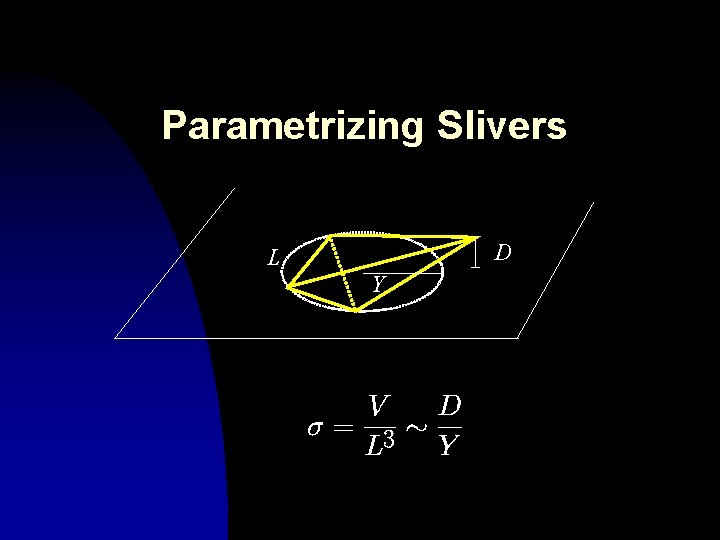
Parametrizing Slivers D L Y

Pumping Lemma (Cheng-Dey-Edelsbrunner-Facello. Teng) z P p H q D Y r s

… under Assumptions n n n Property [r]: the radius-edge ratio the Delaunay triangulation is r. Property [1/3]: for any two points p and q, their weights P, Q < ||p-q|| / 3. Boundary: The Delaunay mesh is periodic

The Stories of Balloons

Interval Lemma 0 n N(p)/3 Constant Degree: The union of all weighted Delaunay triangulations with Property [r] and Property [1/3] has a constant vertex degree

Sliver Removal by Flipping n n n One by one in an arbitrary ordering fix the weight of each point Implementation: flip and keep the best configuration.

Mesh Coarsening

Related and Future Research n n n n n Meshing with a moving boundary Sphere-packing and advancing front Sphere-packing and Hex meshes Meshing for time-and-space Boundary handling in three dimensions Mesh smoothing and improvement Mesh coarsening in three dimensions Software, Software!!! What are the constants in theory and practice

Supports n n DOE ASCI (Center for Simulation of Advanced Rocket) NSF OPAAL (Center for Process Simulation and Design) NSF CAREER Alfred P. Sloan