Delaunay Mesh Generation Tamal K Dey The Ohio

Delaunay Mesh Generation Tamal K. Dey The Ohio State University Department of Computer Science and Engineering 1/43

Delaunay Mesh Generation • Automatic mesh generation with good quality. • Delaunay refinements: • The Delaunay triangulation • lends to a proof structure. And it naturally optimizes certain geometric properties such as min angle. Department of Computer Science and Engineering 2/43

Input/Output • Points P sampled from a surface S in 3 D (don’t know S) Reconstruct S : A simplicial complex K, • (i) K has a geometric realization in 3 D • (ii) |K| homeomorphic to S, • (iii) Hausdorff distance between |K| and S is small • A smooth surface S(or a compact set): • Generate a point sample P from S • Generate a simplicial complex K with vert K=P and satisfying (i), (iii). Department of Computer Science and Engineering 3/43

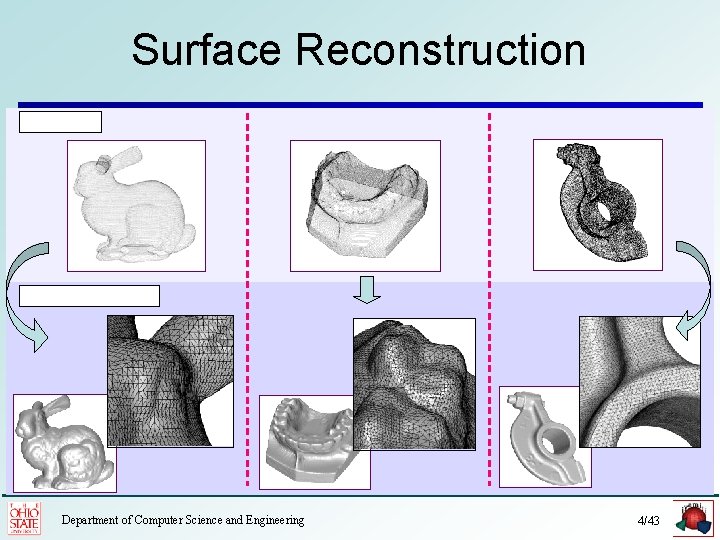
Surface Reconstruction Point Cloud ` Surface Reconstruction Department of Computer Science and Engineering 4/43

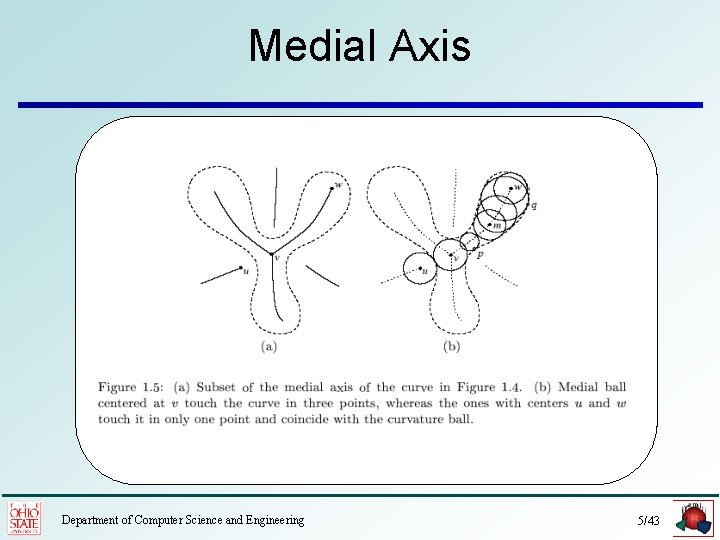
Medial Axis Department of Computer Science and Engineering 5/43

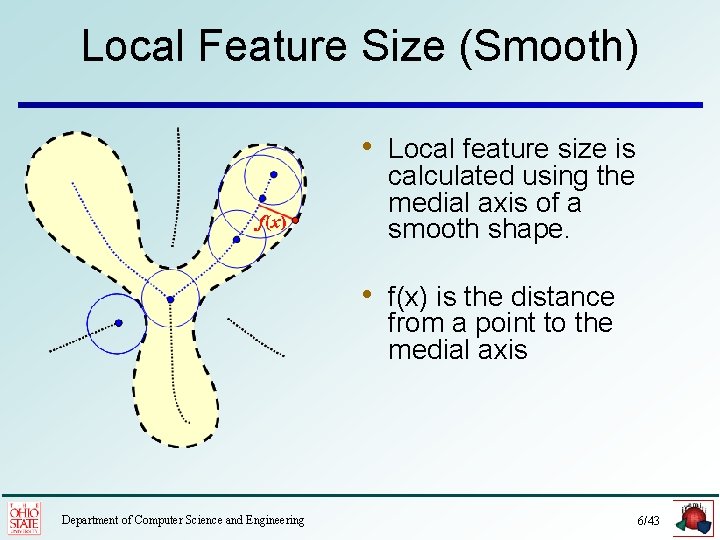
Local Feature Size (Smooth) • Local feature size is calculated using the medial axis of a smooth shape. • f(x) is the distance from a point to the medial axis Department of Computer Science and Engineering 6/43

-Sample [ABE 98] x Each x has a sample within f(x) distance Department of Computer Science and Engineering 7/43

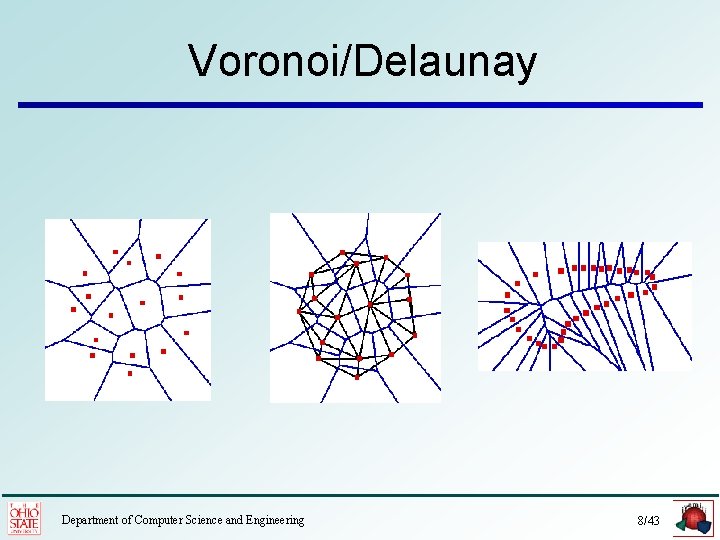
Voronoi/Delaunay Department of Computer Science and Engineering 8/43

Normal and Voronoi Cells(3 D) [Amenta-Bern So. CG 98] Department of Computer Science and Engineering 9/43

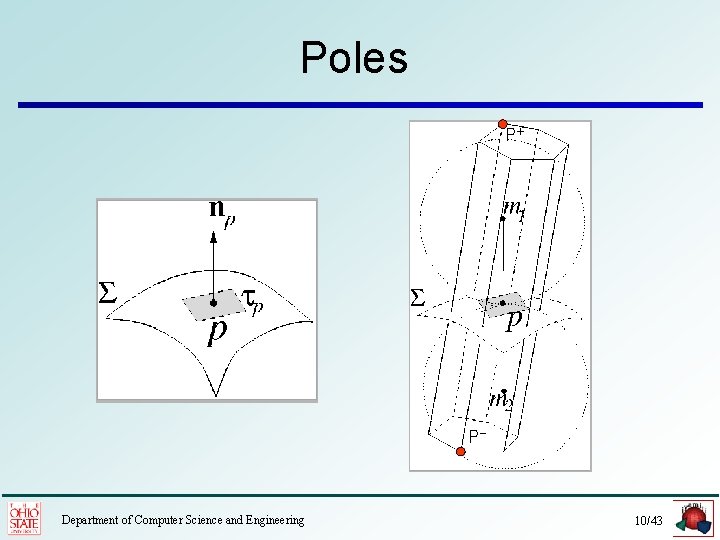
Poles P+ P- Department of Computer Science and Engineering 10/43

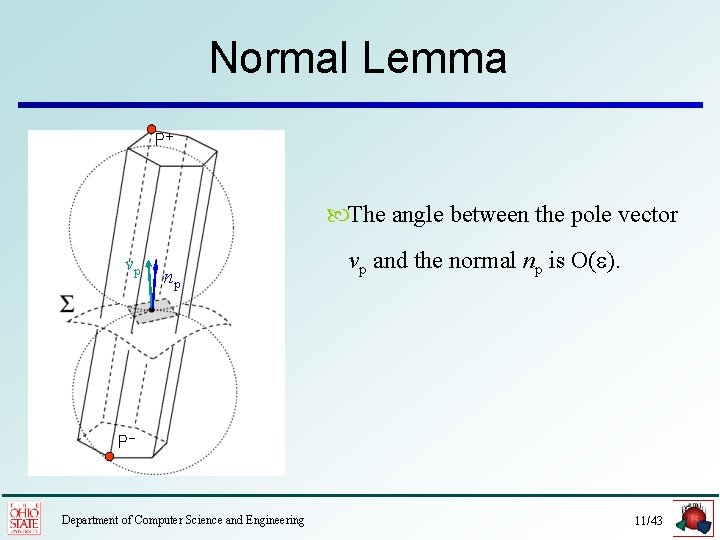
Normal Lemma P+ The angle between the pole vector vp np vp and the normal np is O( ). P- Department of Computer Science and Engineering 11/43

Restricted Delaunay • If the point set is sampled from a domain D. • We can define the restricted Delaunay triangulation, denoted Del P|D. • Each simplex Del P|D is the dual of a Voronoi face V that has a nonempty intersection with the domain D. Department of Computer Science and Engineering 12/43

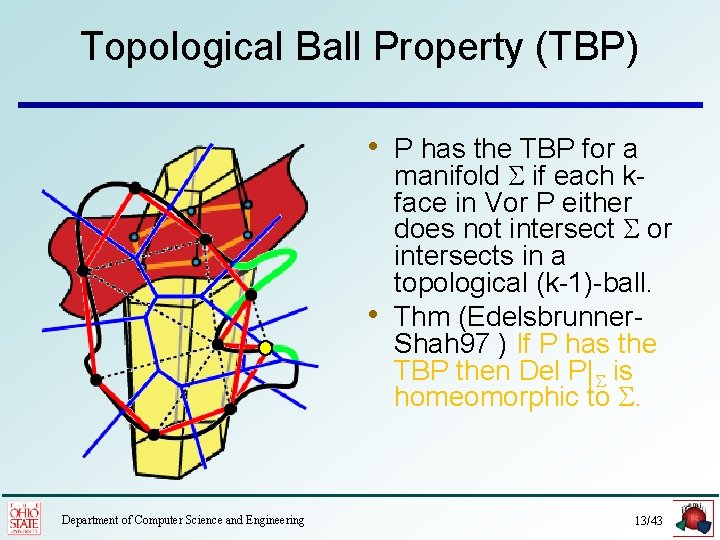
Topological Ball Property (TBP) • P has the TBP for a • Department of Computer Science and Engineering manifold S if each kface in Vor P either does not intersect S or intersects in a topological (k-1)-ball. Thm (Edelsbrunner. Shah 97 ) If P has the TBP then Del P|S is homeomorphic to S. 13/43

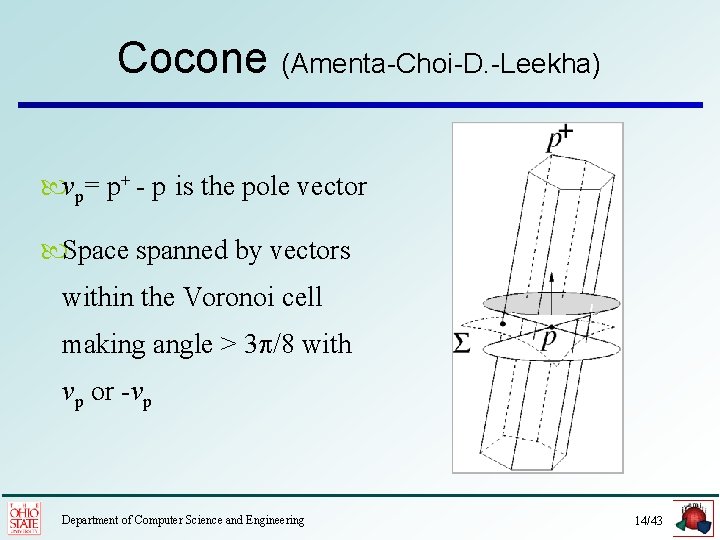
Cocone (Amenta-Choi-D. -Leekha) vp= p+ - p is the pole vector Space spanned by vectors within the Voronoi cell making angle > 3 /8 with vp or -vp Department of Computer Science and Engineering 14/43

Cocone Algorithm Department of Computer Science and Engineering 15/43

Cocone Guarantees Theorem: Any point x S is within O( )f(x) distance from a point in the output. Conversely, any point of output surface has a point x S within O( )f(x) distance. Triangle normals make O( ) angle with true normals at vertices. Theorem: The output surface computed by Cocone from an -sample is homeomorphic to the sampled surface for sufficiently small (<0. 06). Department of Computer Science and Engineering 16/43

Meshing • Input • • Polyhedra Smooth Surfaces Piecewise-smooth Surfaces Non-manifolds & Department of Computer Science and Engineering 17/43

Basics of Delaunay Refinement • Pioneered by Chew 89, Ruppert 92, • Shewchuck 98 To mesh some domain D, 1. Initialize a set of points P D, compute Del P. 2. If some condition is not satisfied, insert a point c from D into P and repeat step 2. 3. Return Del P|D. • Burden is to show that the algorithm terminates (shown by a packing argument). Department of Computer Science and Engineering 18/43

Polyhedral Meshing • Output mesh conforms to input: • All input edges meshed as a • collection of Delaunay edges. All input facets are meshed with a collection of Delaunay triangles. • Algorithms with angle restrictions: • Chew 89, Ruppert 92, Miller-Talmor. Teng-Walkington 95, Shewchuk 98. • Small angles allowed: • Shewchuk 00, Cohen-Steiner- Verdiere-Yvinec 02, Cheng-Poon 03, Cheng-Dey-Ramos-Ray 04, Pav. Walkington 04. Department of Computer Science and Engineering 19/43

Smooth Surface Meshing • Input mesh is either an implicit • surface or a polygonal mesh approximating a smooth surface Output mesh approximates input geometry, conforms to input topology: • No guarantees: • Chew 93. • Skin surfaces: • Cheng-Dey-Edelsbrunner-Sullivan 01. • Provable surface algorithms: • Boissonnat-Oudot 03 and Cheng. Dey-Ramos-Ray 04. • Interior Volumes: • Oudot-Rineau-Yvinec 06. Department of Computer Science and Engineering 21/43

Sampling Theorem Modified Theorem: (Amenta-Bern (Boissonat-Oudot 2005): Theorem 98, Cheng-Dey-Edelsbrunner-Sullivan 01) P SSisisaadiscrete sample so that If. If P -sampleofofa asmoothsurface. SS, eachfor x where a Voronoi edge Delaunay intersects triangulation S lies within f(x) then < 0. 09 the restricted distance from sample, then for <0. 09, the restricted Del P|S has the afollowing properties: Delaunay triangulation Del P|S has the following properties: (i) It is homeomorphic to S (even isotopic embeddings). (ii) Each triangle has normal aligning within O( ) angle to the surface normals (iii) Hausdorff distance between S and Del P|S is O( 2) of the local feature size. Department of Computer Science and Engineering 23/43

Surface Basic Delaunay. Refinement 1. Initialize a set of points P S, compute Del P. 2. If some Voronoi condition is not satisfied, insert a point c edge intersects S at x with from S into and repeat d(x, P)> f(x)Pinsert x in P. step 2. 3. Return Del P|S. Department of Computer Science and Engineering 24/43

Difficulty • How to compute f(x)? • Special surfaces such as skin • surfaces allow easy computation of f(x) [CDES 01] Can be approximated by computing approximate medial axis, needs a dense sample. Department of Computer Science and Engineering 25/43

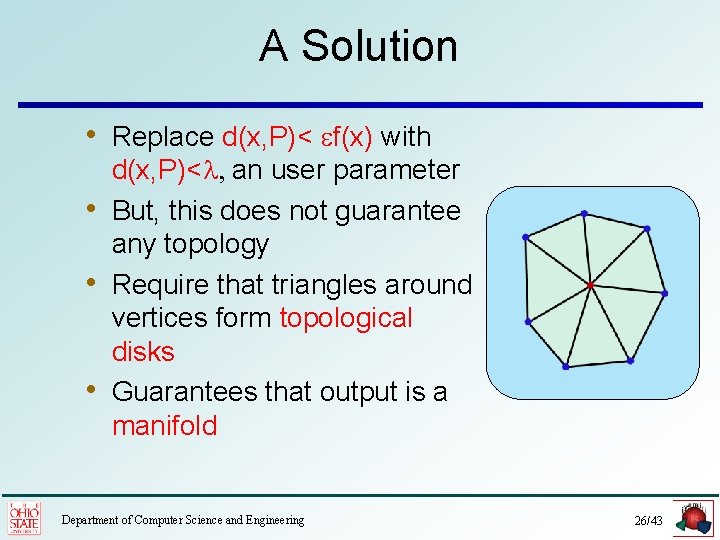
A Solution • Replace d(x, P)< f(x) with • • • d(x, P)<l, an user parameter But, this does not guarantee any topology Require that triangles around vertices form topological disks Guarantees that output is a manifold Department of Computer Science and Engineering 26/43

A Solution Algorithm Del. Surf(S, l) 1. Initialize a set of points P S, compute Del P. 2. (a) If some Voronoi edge intersects M at If some Voronoi edge intersects S xatwith x with d(x, P)> f(x) insert and repeat step 2. d(x, P)> l insert x in P, P, and repeat step 2(a). 2. (b)If restricted triangles around a vertex p do not X=center of largest Surface form a topological disk, x insert furthest x where a dual Delaunay ball Voronoi edge of a triangle around p intersects S. 3. Return Del P|S Department of Computer Science and Engineering 27/43

A Meshing. Theorem: The algorithm Del. Surf produces output mesh with the following guarantees: (i) The output mesh is always a 2 -manifold (ii) If l is sufficiently small, the output mesh satisfies topological and geometric guarantees: 1. It is related to S with an isotopy. 2. Each triangle has normal aligning within O(l) angle to the surface normals 3. Hausdorff distance between S and Del P|S is O(l 2) of the local feature size. Department of Computer Science and Engineering 28/43

Implicit surface Department of Computer Science and Engineering 29/43

Remeshing Department of Computer Science and Engineering 30/43

PSCs – A Large Input Class [Cheng-D. -Ramos 07] • Piecewise smooth complexes (PSCs) include: • Polyhedra • Smooth Surfaces • Piecewise-smooth Surfaces • Non-manifolds & Department of Computer Science and Engineering 31/43

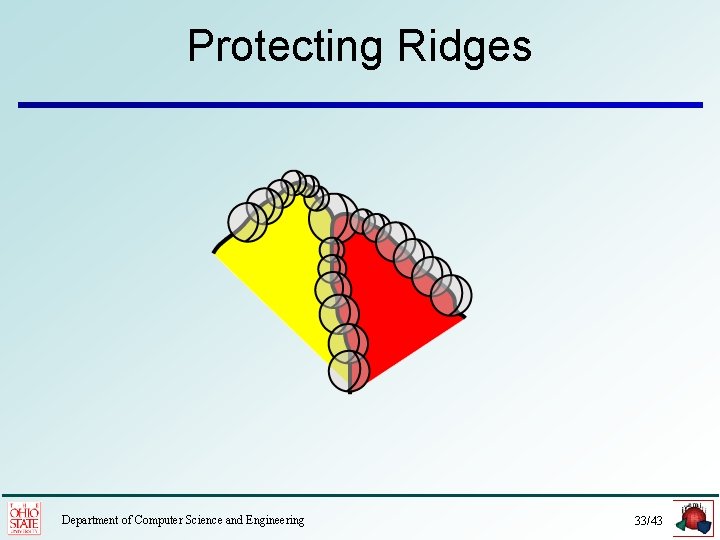
Protecting Ridges Department of Computer Science and Engineering 33/43

Del. PSC Algorithm [Cheng-D. -Ramos-Levine 07, 08] Del. PSC(D, λ) 1. Protect ridges of D using protection balls. 2. Refine in the weighted Delaunay by turning the balls into weighted points. 1. Refine a triangle if it has orthoradius > l. 2. Refine a triangle or a ball if disk condition is violated 3. Refine a ball if it is too big. 3. Return i Deli S|Di Department of Computer Science and Engineering 36/43

Guarantees for Del. PSC 1. Manifold • For each σ D 2, triangles in Del S|σ are a manifold with vertices only in σ. Further, their boundary is homeomorphic to bd σ with vertices only in σ. 2. Granularity • • There exists some λ > 0 so that the output of Del. PSC(D, λ) is homeomorphic to D. This homeomorphism respects stratification, For 0 ≤ i ≤ 2, and σ Di, Del S|σ is homemorphic to σ too. Department of Computer Science and Engineering 37/43

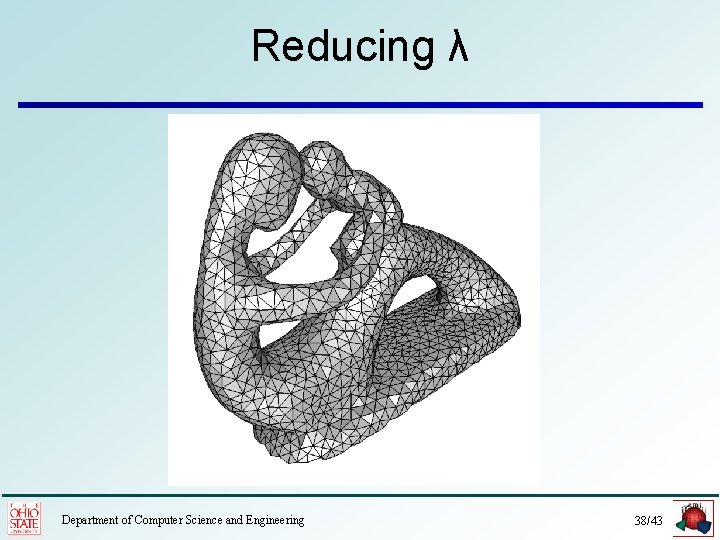
Reducing λ Department of Computer Science and Engineering 38/43

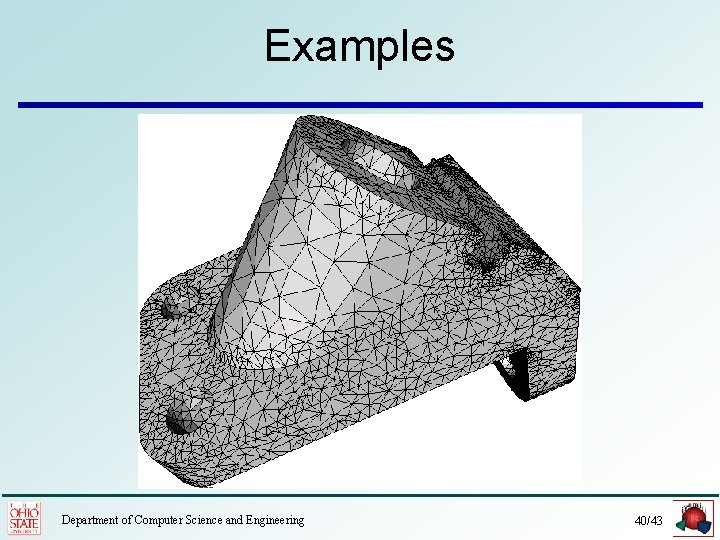
Examples Department of Computer Science and Engineering 40/43

Examples Department of Computer Science and Engineering 42/43

Some Resources • Software available from http: //www. cse. ohio-state. edu/~tamaldey/cocone. html http: //www. cse. ohio-state. edu/~tamaldey/delpsc. html http: //www. cse. ohio-state. edu/~tamaldey/locdel. html Open : Reconstruct piecewise smooth surfaces, non-manifolds Open: Guarantee quality of all tetrahedra in volume meshing A book Delaunay Mesh Generation: w/ S. -W. Cheng, J. Shewchuk (2012) Department of Computer Science and Engineering 43/43

Thank You! Department of Computer Science and Engineering 44/43