Degenerate Quantum Gases on a Chip Dept Of

Degenerate Quantum Gases on a Chip Dept. Of Physics, University of Toronto Prof: Joseph Thywissen Post Docs: Seth Aubin Stefan Myrskog Ph. D. Students: Marcius Extavour M. Sc. Students: Lindsay Le. Blanc Undergrads: Research Technologist: Barbara Cieslak Ian Leroux Alan Stummer

Outline • • • Quantum Gases – Bosons (87 Rb) + Fermions (40 K) Laser Cooling Magnetic Traps Chip Traps Evaporative/Sympathetic Cooling Outlook 10 -13 thermal atoms 10 -6 MOT magnetic traps 1 evap. cooling BEC / DFG 105 psd science!

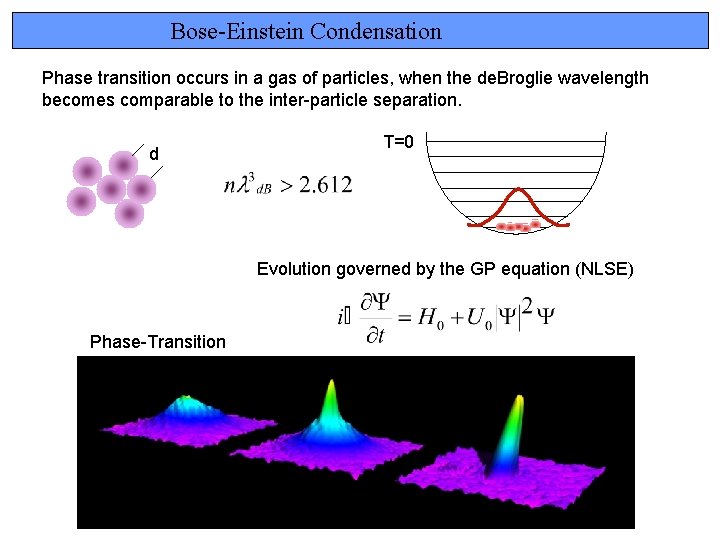
Bose-Einstein Condensation Phase transition occurs in a gas of particles, when the de. Broglie wavelength becomes comparable to the inter-particle separation. d T=0 Evolution governed by the GP equation (NLSE) Phase-Transition

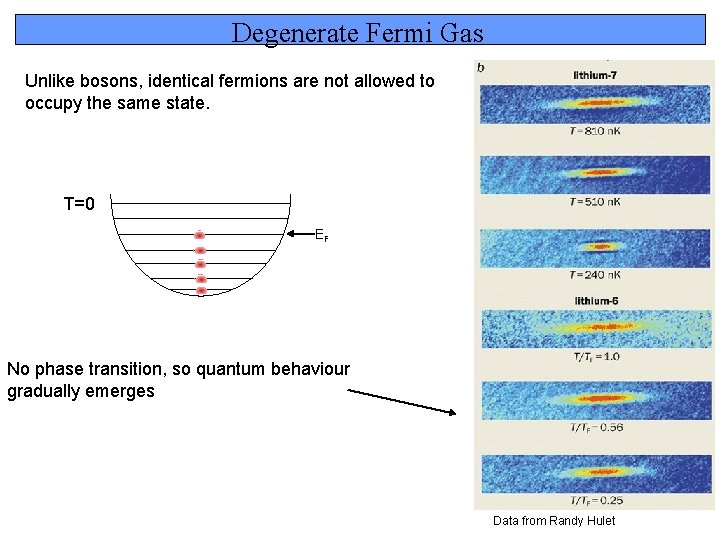
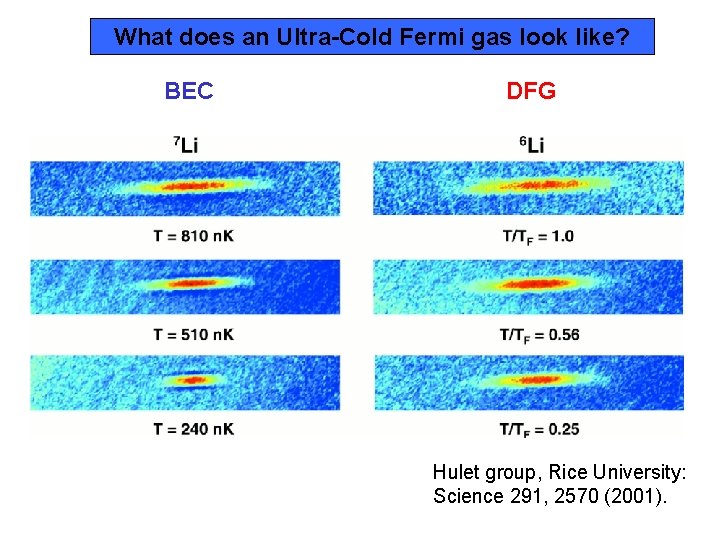
Degenerate Fermi Gas Unlike bosons, identical fermions are not allowed to occupy the same state. T=0 EF No phase transition, so quantum behaviour gradually emerges Data from Randy Hulet

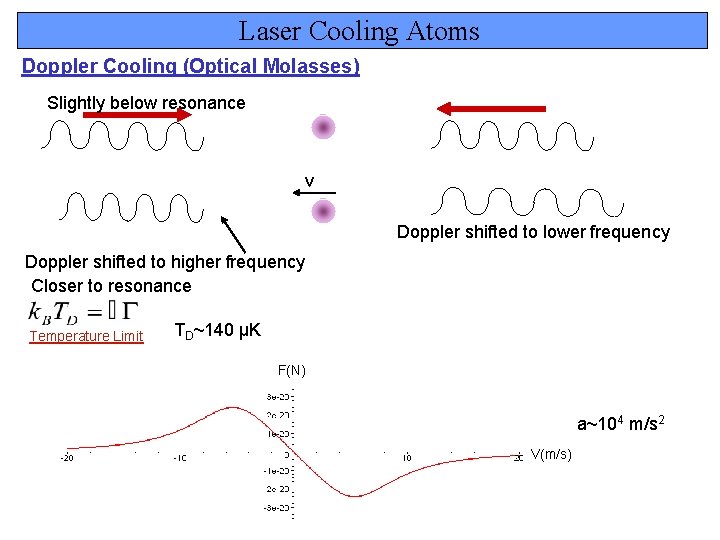
Laser Cooling Atoms Doppler Cooling (Optical Molasses) Slightly below resonance v Doppler shifted to lower frequency Doppler shifted to higher frequency Closer to resonance Temperature Limit TD~140 μK F(N) a~104 m/s 2 V(m/s)

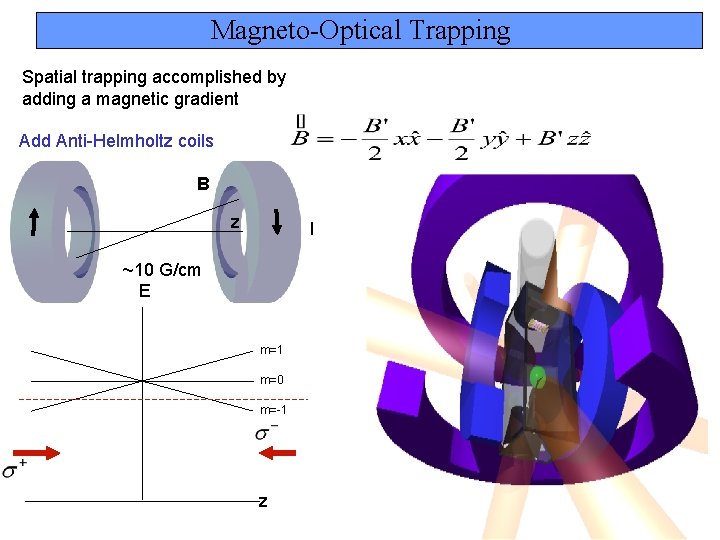
Magneto-Optical Trapping Spatial trapping accomplished by adding a magnetic gradient Add Anti-Helmholtz coils B z I ~10 G/cm E m=1 m=0 m=-1 z

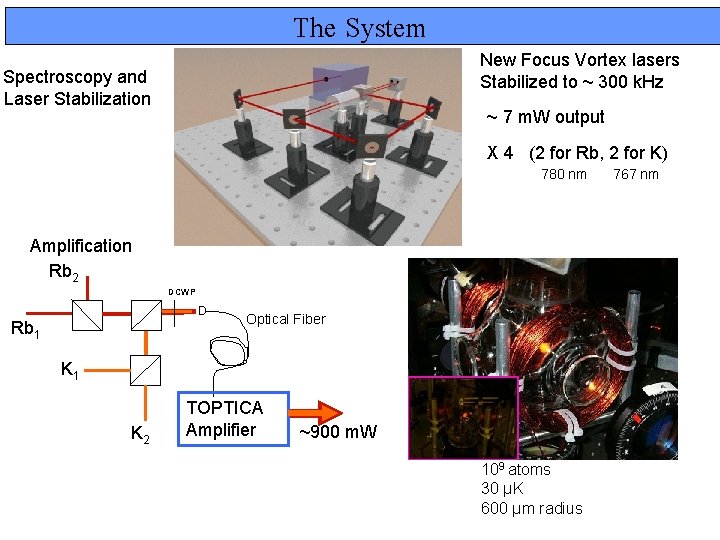
The System New Focus Vortex lasers Stabilized to ~ 300 k. Hz Spectroscopy and Laser Stabilization ~ 7 m. W output X 4 (2 for Rb, 2 for K) 780 nm Amplification Rb 2 DCWP D Rb 1 Optical Fiber K 1 K 2 TOPTICA Amplifier ~900 m. W 109 atoms 30 μK 600 μm radius 767 nm

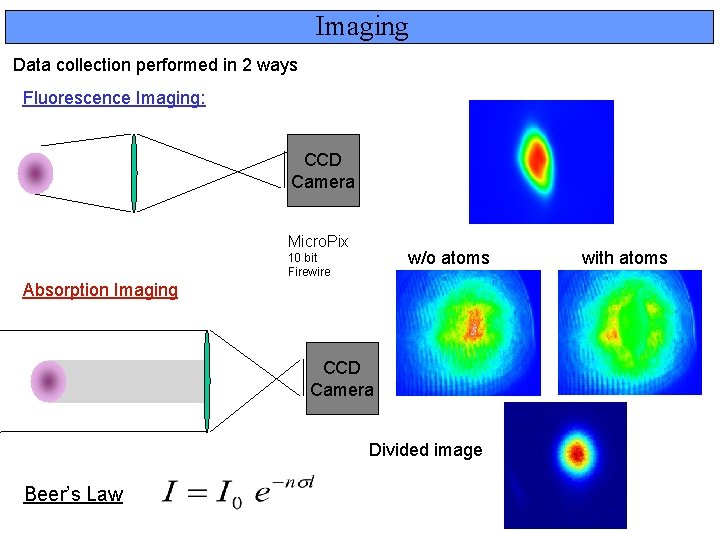
Imaging Data collection performed in 2 ways Fluorescence Imaging: CCD Camera Micro. Pix w/o atoms 10 bit Firewire Absorption Imaging CCD Camera Divided image Beer’s Law with atoms

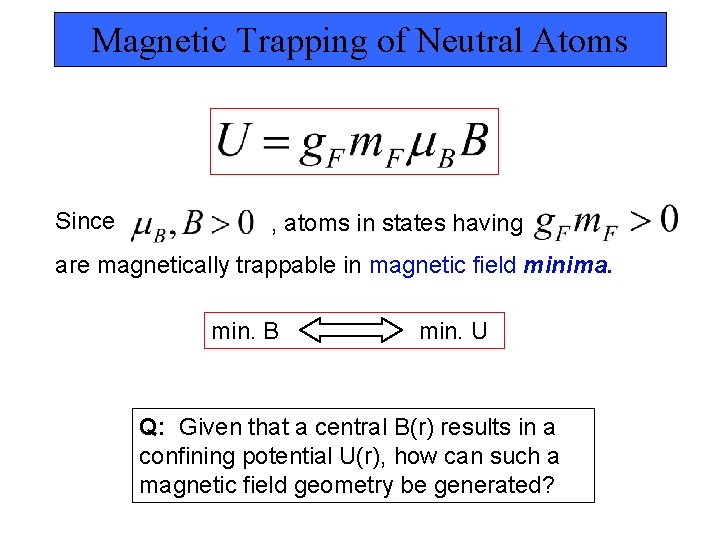
Magnetic Trapping of Neutral Atoms Interaction between external magnetic field and atomic magnetic moment: B For an atom in a state having total angular momentum F. where For an atom in the arbitrary hyperfine state so that .

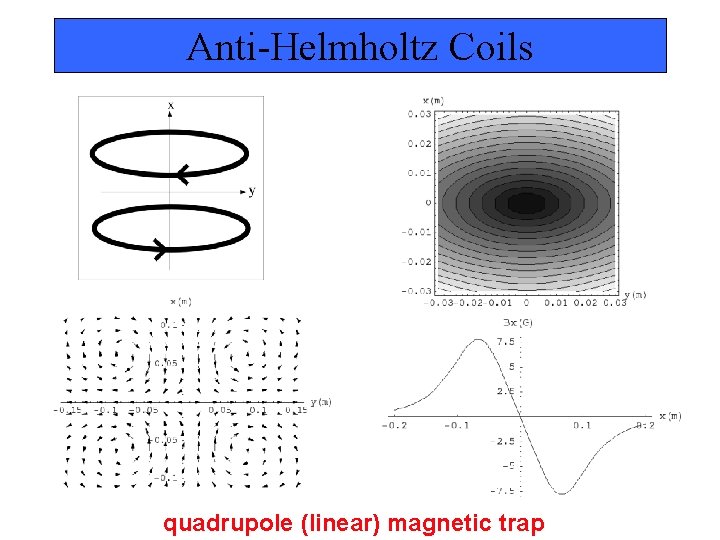
Magnetic Trapping of Neutral Atoms Since , atoms in states having are magnetically trappable in magnetic field minima. min. B min. U Q: Given that a central B(r) results in a confining potential U(r), how can such a magnetic field geometry be generated?

Anti-Helmholtz Coils quadrupole (linear) magnetic trap

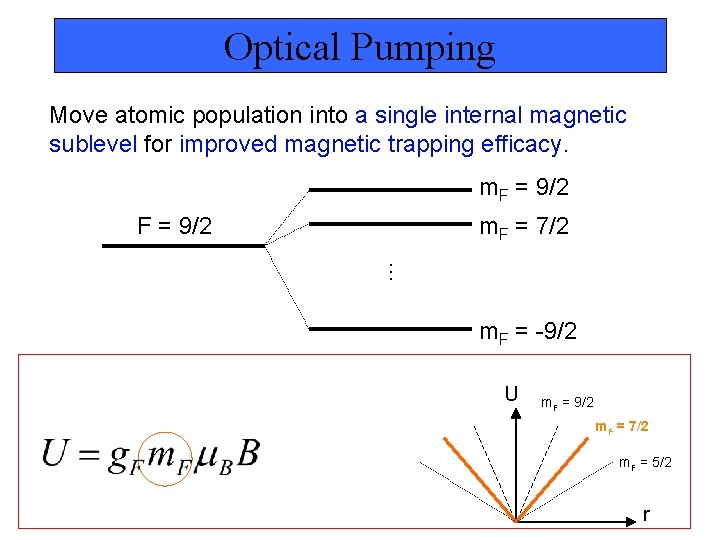
Optical Pumping Move atomic population into a single internal magnetic sublevel for improved magnetic trapping efficacy. m. F = 9/2 m. F = 7/2 … F = 9/2 m. F = -9/2 U m. F = 9/2 m. F = 7/2 m. F = 5/2 r

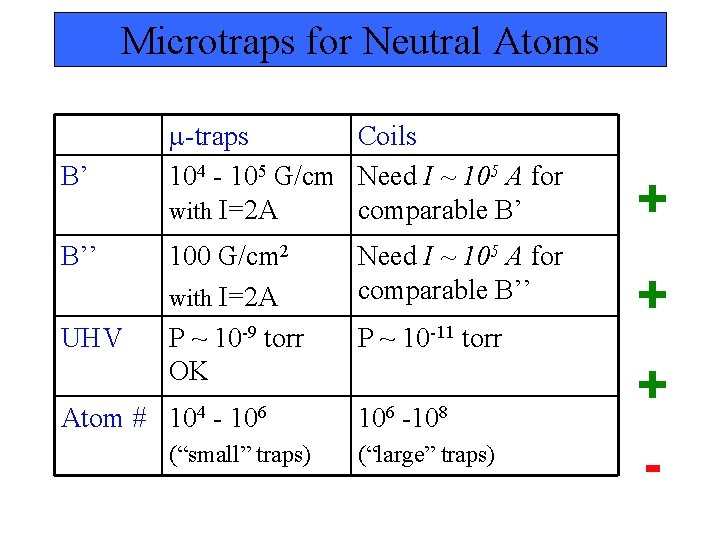
Microtraps for Neutral Atoms B’ B’’ UHV Atom # -traps Coils 104 - 105 G/cm Need I ~ 105 A for with I=2 A comparable B’ 100 G/cm 2 with I=2 A P ~ 10 -9 torr OK Need I ~ 105 A for comparable B’’ 104 106 - 106 (“small” traps) P ~ 10 -11 torr -108 (“large” traps) + + + -

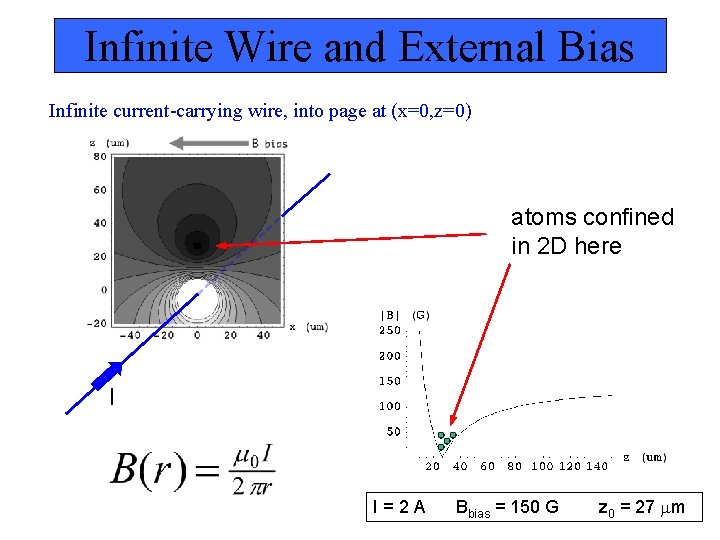
Infinite Wire and External Bias Infinite current-carrying wire, into page at (x=0, z=0) atoms confined in 2 D here I I=2 A Bbias = 150 G z 0 = 27 m

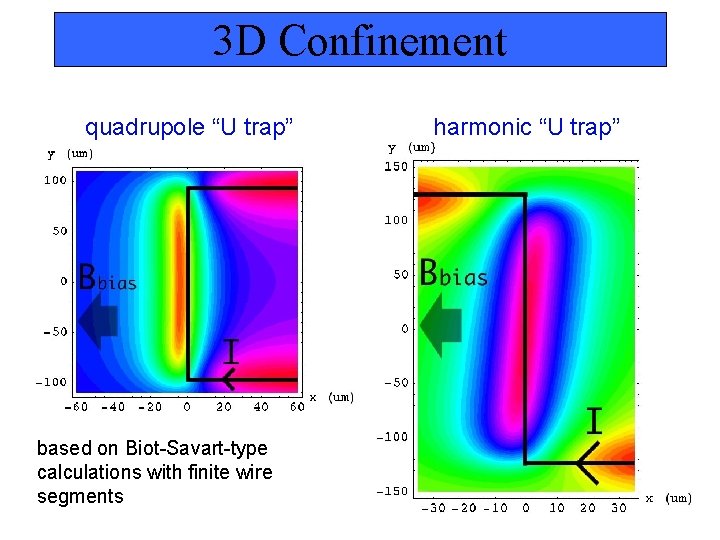
3 D Confinement quadrupole “U trap” based on Biot-Savart-type calculations with finite wire segments harmonic “U trap”

Orsay Chip 16 mm 28 mm • gold conductors (yellow) on Si. O 2 -coated Si wafer • wire widths from 20 to 460 m • wire heights of 7 m

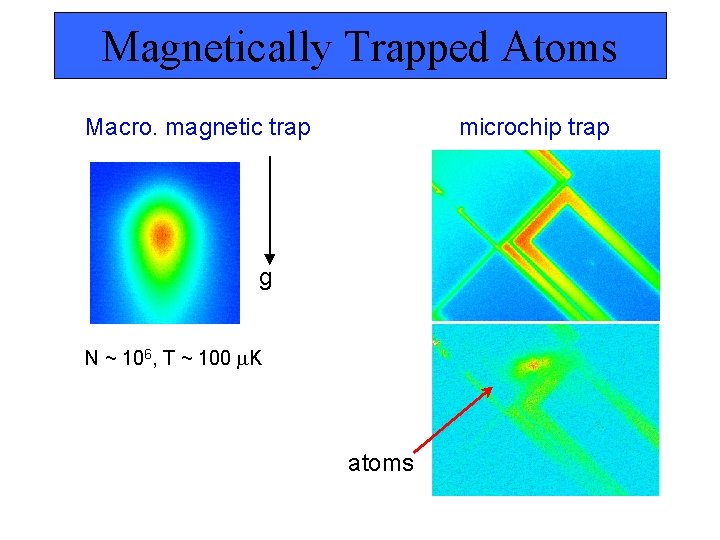
Magnetically Trapped Atoms Macro. magnetic trap microchip trap g N ~ 106, T ~ 100 K atoms

Stack • physical support of atom chip in UHV chamber (macor clamps) • electrical connections • heat-sinking • atom-dispensers

Evaporative Cooling Remove most energetic (hottest) atoms Wait for atoms to rethermalize among themselves Wait time is given by the elastic collision rate kelastic = n v Macro-trap: low initial density, evaporation time ~ 10 -30 s. Micro-trap: high initial density, evaporation time ~ 1 -2 s.

Runaway Evaporation 1. Evaporate atoms remaining atoms get colder. Natoms decreases. 2. Atoms are less energetic Atoms stay closer to trap center. Volume decreases. 3. If n=Natoms/Volume increases then atoms undergo runaway evaporation. Phase space density: Typically, 999 out of 1000 atoms are evaporated for 1 BEC atom.

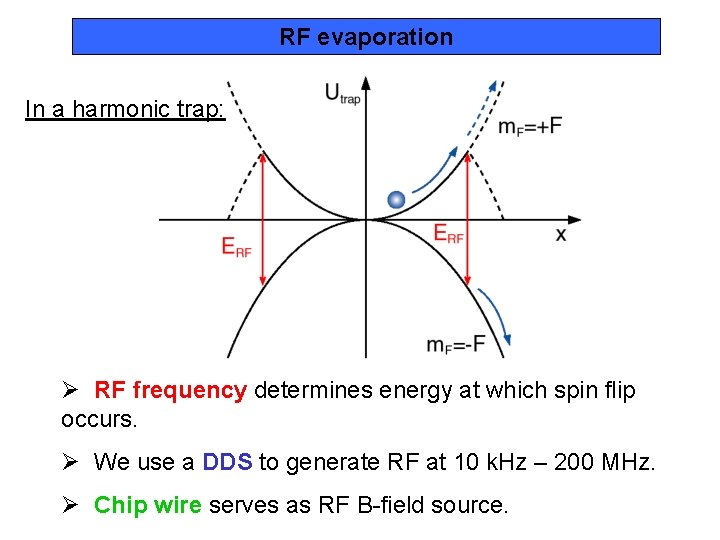
RF evaporation In a harmonic trap: Ø RF frequency determines energy at which spin flip occurs. Ø We use a DDS to generate RF at 10 k. Hz – 200 MHz. Ø Chip wire serves as RF B-field source.

Direct Digitial Synthesizer (DDS) Pulse Timing Control Sequencer chip

The problem with Fermions In traps with very low temperatures, If , then two atoms must scatter as an s-wave: s-wave is symmetric under exchange of particles: as T 0: Ø Identical Bosons undergo s-wave scattering. Ø Identical Fermions cannot scatters as s-waves. identical Fermions do not scatter (i. e. interact).

Sympathetic Cooling Problem: Cold identical fermions do not interact (cannot rethermalize) No evaporative cooling Solution: add non-identical particles s-wave scattering permitted We cool our fermionic 40 K atoms sympathetically with an 87 Rb BEC. 2 possibilities: 1. Evaporate 40 K and 87 Rb mixture simultaneously. 2. Evaporate 87 Rb only, while 40 K cools through thermal contact.

What does an Ultra-Cold Fermi gas look like? BEC DFG Hulet group, Rice University: Science 291, 2570 (2001).

Condensed Matter Physics Applications 1. BCS Cooper pairing in an ultra-cold fermi gas. 2. no clean signature yet. 2. Quantum simulation of the Fermi-Hubbard model. 3. not solved numerically or analytically. 4. proposed model for high-Tc 5. superconductors. 6. 3. Low dimensional system. Optical lattice for Fermi. Hubbard model. 7. 1 -D Fermi gas: Luttinger-Tomonaga liquid 8. 1 -D Bose gas: Tonks gas.

Interferometry Applications of Degenerate Fermions BEC DFG Good: Heisenberg limited momentum spread. Good: Vanishing atom-atom interactions. Bad: large density dependent atom-atom interactions. Less good: small momentum spread. 1. Atomic Clocks (temporal interferometer -- exp(i t) ) 2. DFG significantly reduces collision shift (clock shift). 3. 2. Spatial interferometers – exp(ikz): k=2 mv/h 4. 780 nm photon: k=8 106 m-1, 87 Rb at 1 m/s: k=1. 4 109 m-1

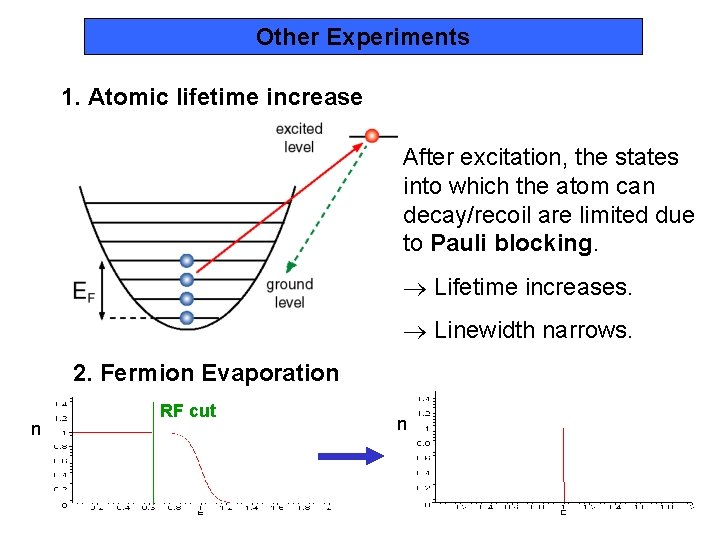
Other Experiments 1. Atomic lifetime increase After excitation, the states into which the atom can decay/recoil are limited due to Pauli blocking. Lifetime increases. Linewidth narrows. 2. Fermion Evaporation n RF cut n

Outlook Current Status: Ø 40 K and 87 Rb laser frequency and amplification set-up. Ø 39 K MOT, 87 Rb MOT. Ø 87 Rb quadrupole magnetic trap. Ø 87 Rb transported to chip. Ø 87 Rb loaded into chip U-trap. Next Steps: Ø load chip Z-trap, RF evaporation, BEC. Ø 40 K MOT, DFG.

Group Members Marcius Extavour Lindsay Le. Blanc Joseph Thywissen Stefan Myrskog Seth Aubin Barbara Cieslak Alan Stummer Ian Leroux