Degenerate Fermi Gas Ground State of a Fermi







![Neutron Stars [ M=(1. 4 -3)M ] For a dead star more massive than Neutron Stars [ M=(1. 4 -3)M ] For a dead star more massive than](https://slidetodoc.com/presentation_image/1d3a33559435c8d16b37fbbe69e13d0e/image-12.jpg)
- Slides: 19

Degenerate Fermi Gas • • • Ground State of a Fermi Gas, Fermi Energy Fermi Velocity, Fermi Momentum, Fermi Pressure and Stellar Evolution Non-Zero T, Fermi-Dirac Distribution Specific Heat of Degenerate Fermi Gas When we consider ensembles of identical particles, we need to distinguish two regimes: the low-density limit (the inter-particle distance is much greater than the de Broglie wavelength of these particles) and the high-density limit (the opposite is true). In the low-density limit, bosonic and fermionic ensembles behave in a similar way (Boltzmann statistics). In the high-density limit, fermions and bosons are quite different! high-density limit n. C depends on T ! The high-density limit is also referred to as the degeneracy limit. The degeneracy requirement can be formulated in terms of the so-called degeneracy temperature of the gas, TC which corresponds to the condition n~ n. Q: For fermions: TC ~ EF/k. B where EF is the Fermi energy (see below), for bosons: TC is the temperature of BE condensation.

Ground State of a Fermi Gas, Fermi Energy In the next two lectures, we’ll consider ideal gases of fermions and bosons. In an ideal gas, particles do not interact with one another (unless they collide, and even these processes are not likely because we consider point-like particles). Thus, when we consider an ideal gas of charged particles, we’ll assume that their charges are “screened” at short distances: e. g. , the negative charge of electrons in metals is screened by the positive charge of ions (btw, this is not the case for the protons in nuclei). The ground state (T=0) of a system of fermions is governed by the Pauli Exclusion Principle: all the low-energy states are filled to a certain maximum energy EF which depends on the density of the fermionic “gas” (the so-called Fermi energy). Occupancy (= the distribution function): the mean number of fermions in a particular quantum state While the occupancy f(�) is often less than unity, it is not a probability: n=N/V – the average density of particles Fermi energy: the max energy of an individual fermion in the ground state = the increase of the ground-sate energy when a single fermion is added to the system. Example: N fermions in a 1 D square well

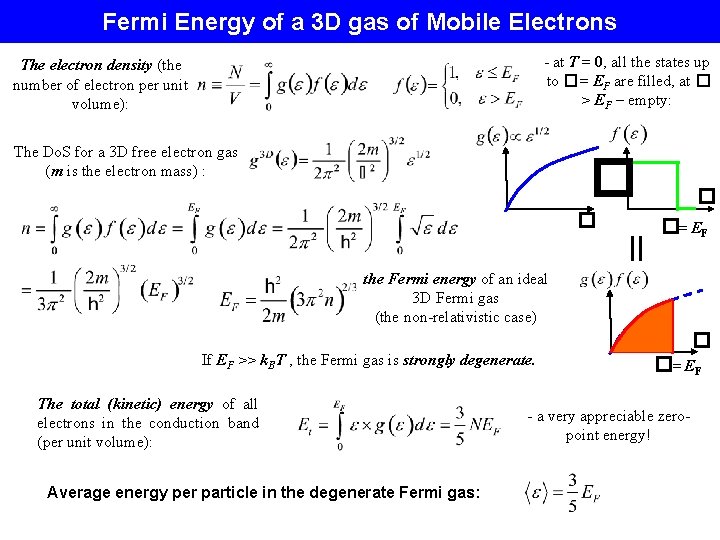
Fermi Energy of a 3 D gas of Mobile Electrons - at T = 0, all the states up to �= EF are filled, at � > EF – empty: The electron density (the number of electron per unit volume): The Do. S for a 3 D free electron gas (m is the electron mass) : � � � = �= EF the Fermi energy of an ideal 3 D Fermi gas (the non-relativistic case) � If EF >> k. BT , the Fermi gas is strongly degenerate. The total (kinetic) energy of all electrons in the conduction band (per unit volume): Average energy per particle in the degenerate Fermi gas: �= EF - a very appreciable zeropoint energy!

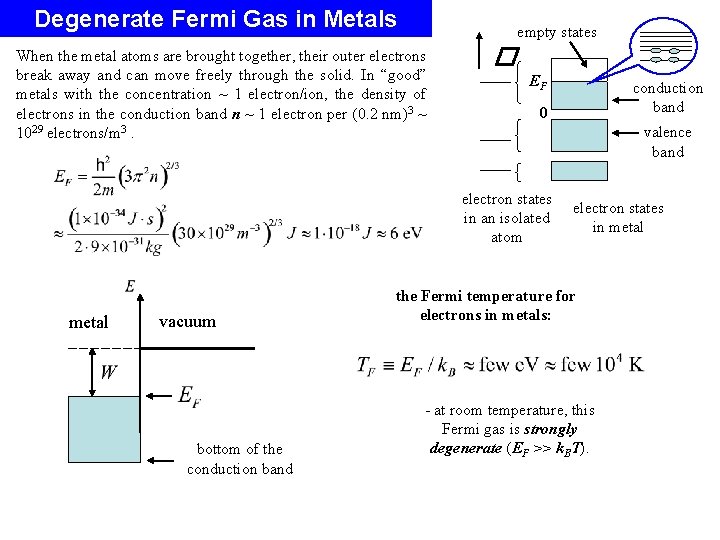
Degenerate Fermi Gas in Metals empty states When the metal atoms are brought together, their outer electrons break away and can move freely through the solid. In “good” metals with the concentration ~ 1 electron/ion, the density of electrons in the conduction band n ~ 1 electron per (0. 2 nm)3 ~ 1029 electrons/m 3. � EF 0 valence band electron states in an isolated atom metal vacuum bottom of the conduction band electron states in metal the Fermi temperature for electrons in metals: - at room temperature, this Fermi gas is strongly degenerate (EF >> k. BT).

Problem (Final 2008) (a) (10) Estimate the magnitude of thermal de Broglie wavelength (K � k. BT) for an electron at room temperature. Using this estimate, explain why Boltzmann statistics cannot be applied to the mobile electrons in copper. The density of mobile electrons in copper is 8. 5· 1028 m-3, the effective mass = the mass of a free electron. - Fermi distribution (b) (7) Calculate the Fermi energy for mobile electrons in Cu. Is room temperature sufficiently low to treat this system as degenerate electron gas? Explain. - strongly degenerate

The Fermi Gas of Nucleons in a Nucleus Let’s consider the system of nucleons in a large nucleus (both protons and neutrons are fermions). In heavy elements, the number of nucleons in the nucleus is large and statistical treatment is a reasonable approximation. We need to estimate the density of protons/neutrons in the nucleus. The radius of the nucleus that contains A nucleons: Thus, the density of nucleons is: For simplicity, we assume that the # of protons = the # of neutrons, hence their density is The Fermi energy EF >>> k. BT – at room temperature, the system is strongly degenerate (all nucleons are in their ground state) The average kinetic energy in a degenerate Fermi gas = 0. 6 of the Fermi energy - the nucleons are non-relativistic

Fermi Velocity and Fermi Momentum (non-relativistic gas) In metals, the electrons at the Fermi level are moving at a very high speed (at T=0!): - v. F is the Fermi velocity When an electron is confined in a very small space, it "flies about its tiny cell at high speed, kicking with great force against adjacent electrons in their cells. This degenerate motion. . . cannot be stopped by cooling the matter. Nothing can stop it; it is forced on the electron by the laws of quantum mechanics, even when the matter is at absolute zero temperature" (Thorne 1994). This velocity is of the same order of magnitude as the orbital velocity of the outer electrons in an atom, and ~10 times the mean thermal velocity that a non-degenerate electron gas would have at room temperature. Still, since v. F<<c, we can treat the mobile electrons as non-relativistic particles. The corresponding momentum: the Fermi momentum

Pressure of a Degenerate (non-relativistic) Fermi Gas The pressure of a degenerate Fermi gas (Fermi or degeneracy pressure) at T=0 can be very high (in stark contrast to the classical ideal gas described by the equation of state PV=RT) density n v. F � 1 s 1 m 2 assuming all electrons have the same v and 1/6 of them move towards the wall exact result obtained by integration over all angles and velocities The degeneracy pressure depends on n (as n 5/3) and does not depend on T at T << EF. Let’s estimate this pressure for a typical metal: In metals, this enormous pressure is counteracted by the Coulomb attraction of the electrons to the positive ions. !

Fermi Pressure and Stellar Evolution How stars can support themselves against gravity: • gas and radiation pressure supports stars in which reactions occur thermonuclear • pressure of a degenerate electron gas at high densities supports the objects with no fusion: dead stars (white dwarfs) and the cores of giant planets (Jupiter, Saturn) • pressure of a degenerate neutron gas at high densities support stars 3 Msun 1. 4 Msun neutron

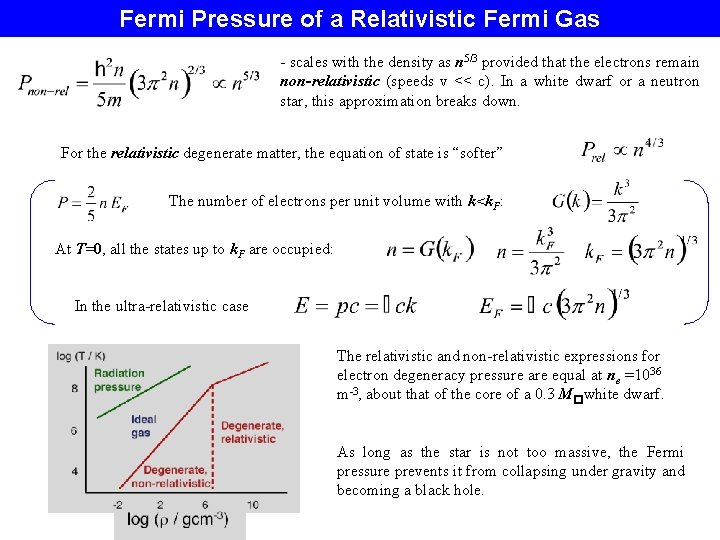
Fermi Pressure of a Relativistic Fermi Gas - scales with the density as n 5/3 provided that the electrons remain non-relativistic (speeds v << c). In a white dwarf or a neutron star, this approximation breaks down. For the relativistic degenerate matter, the equation of state is “softer” The number of electrons per unit volume with k<k. F: At T=0, all the states up to k. F are occupied: In the ultra-relativistic case The relativistic and non-relativistic expressions for electron degeneracy pressure are equal at ne =1036 m-3, about that of the core of a 0. 3 M�white dwarf. As long as the star is not too massive, the Fermi pressure prevents it from collapsing under gravity and becoming a black hole.

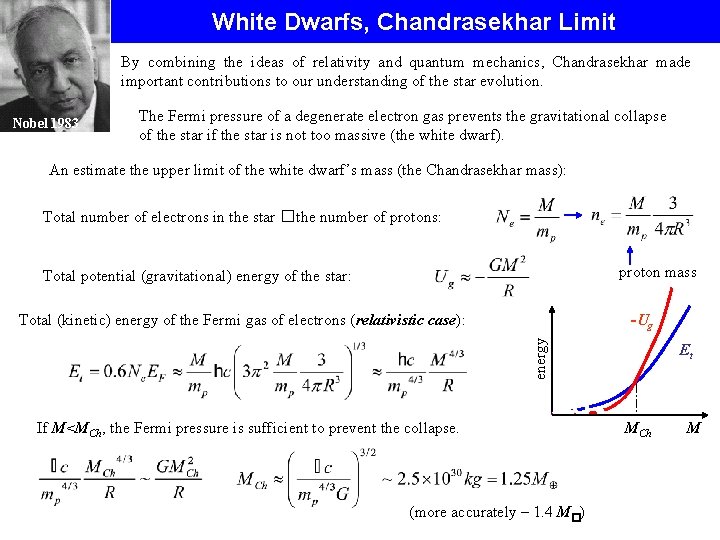
White Dwarfs, Chandrasekhar Limit By combining the ideas of relativity and quantum mechanics, Chandrasekhar made important contributions to our understanding of the star evolution. Nobel 1983 The Fermi pressure of a degenerate electron gas prevents the gravitational collapse of the star is not too massive (the white dwarf). An estimate the upper limit of the white dwarf’s mass (the Chandrasekhar mass): Total number of electrons in the star �the number of protons: proton mass Total potential (gravitational) energy of the star: -Ug energy Total (kinetic) energy of the Fermi gas of electrons (relativistic case): If M<MCh, the Fermi pressure is sufficient to prevent the collapse. (more accurately – 1. 4 M�) Et MCh M
![Neutron Stars M1 4 3M For a dead star more massive than Neutron Stars [ M=(1. 4 -3)M ] For a dead star more massive than](https://slidetodoc.com/presentation_image/1d3a33559435c8d16b37fbbe69e13d0e/image-12.jpg)
Neutron Stars [ M=(1. 4 -3)M ] For a dead star more massive than 1. 4 MSun, the electron degeneracy pressure cannot prevent the gravitational collapse. During the collapse an extra energy liberated is sufficient to drive a nuclear reaction: If the mass is not too high (<3 MSun), the further contraction is stopped by the degeneracy pressure of neutrons (otherwise – black hole). By knowing the parameters of neutron stars, we can explain why these stars are made of neutrons. A typical neutron star has a mass like the Sun (MSun = 2 × 1033 g), but a much smaller radius R ~10 km. The Fermi energy of the neutrons: EF � 30 Me. V. The neutron density: n ~ 1044 m-3 comparable to the nuclear density Let consider a hypothetical star made of protons and electrons, each with the concentration n ~ 1044 m 3 (the # of protons = the # of electrons, the star is electrically neutral). The Fermi energy for protons would be nearly the same as that for the neutrons. On the other hand, the electron EF would be greater: by the ratio Mn/me ~1838 in the non-relativistic case, but we need to consider ultra-relativistic electrons. For ultra-relativistic electrons with this density EF ~280 Me. V! Obviously, the energy difference EF(electrons)-EF(neutrons) is sufficient to drive the nuclear reaction Note that in a white dwarf [n ~ 1036 m-3 EF(electrons) � 0. 5 Me. V], this reaction is still energetically unfavorable:

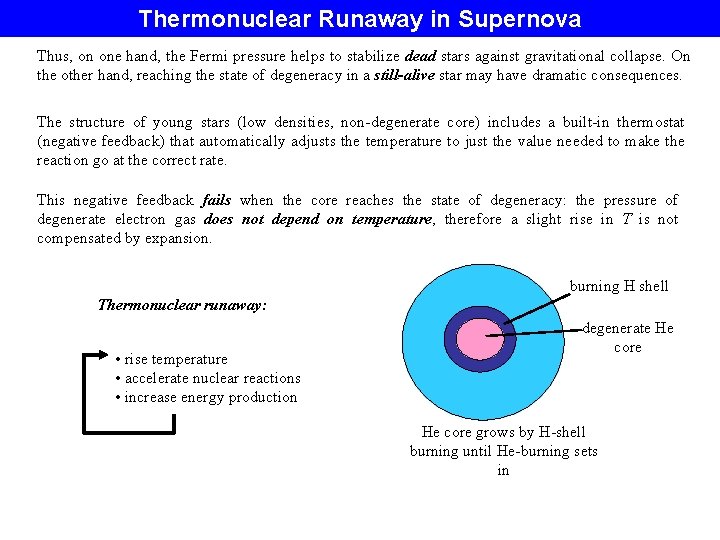
Thermonuclear Runaway in Supernova Thus, on one hand, the Fermi pressure helps to stabilize dead stars against gravitational collapse. On the other hand, reaching the state of degeneracy in a still-alive star may have dramatic consequences. The structure of young stars (low densities, non-degenerate core) includes a built-in thermostat (negative feedback) that automatically adjusts the temperature to just the value needed to make the reaction go at the correct rate. This negative feedback fails when the core reaches the state of degeneracy: the pressure of degenerate electron gas does not depend on temperature, therefore a slight rise in T is not compensated by expansion. burning H shell Thermonuclear runaway: • rise temperature • accelerate nuclear reactions • increase energy production degenerate He core grows by H-shell burning until He-burning sets in

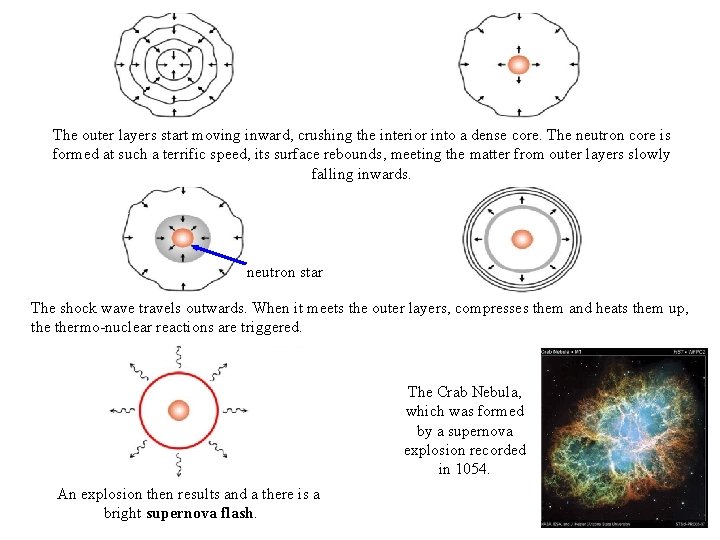
The outer layers start moving inward, crushing the interior into a dense core. The neutron core is formed at such a terrific speed, its surface rebounds, meeting the matter from outer layers slowly falling inwards. neutron star The shock wave travels outwards. When it meets the outer layers, compresses them and heats them up, thermo-nuclear reactions are triggered. The Crab Nebula, which was formed by a supernova explosion recorded in 1054. An explosion then results and a there is a bright supernova flash.

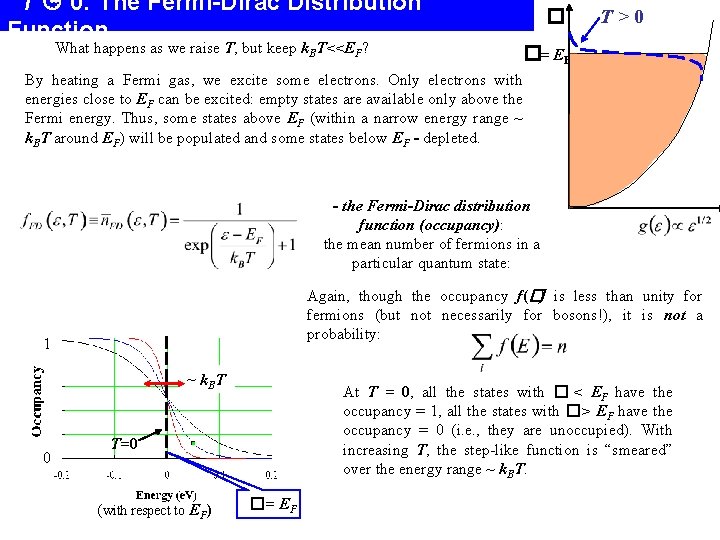
T 0: The Fermi-Dirac Distribution Function What happens as we raise T, but keep k. BT<<EF? � T>0 �= EF By heating a Fermi gas, we excite some electrons. Only electrons with energies close to EF can be excited: empty states are available only above the Fermi energy. Thus, some states above EF (within a narrow energy range ~ k. BT around EF) will be populated and some states below EF - depleted. - the Fermi-Dirac distribution function (occupancy): the mean number of fermions in a particular quantum state: Again, though the occupancy f(�) is less than unity for fermions (but not necessarily for bosons!), it is not a probability: 1 ~ k. BT 0 At T = 0, all the states with � < EF have the occupancy = 1, all the states with � > EF have the occupancy = 0 (i. e. , they are unoccupied). With increasing T, the step-like function is “smeared” over the energy range ~ k. BT. T =0 (with respect to EF) � = EF

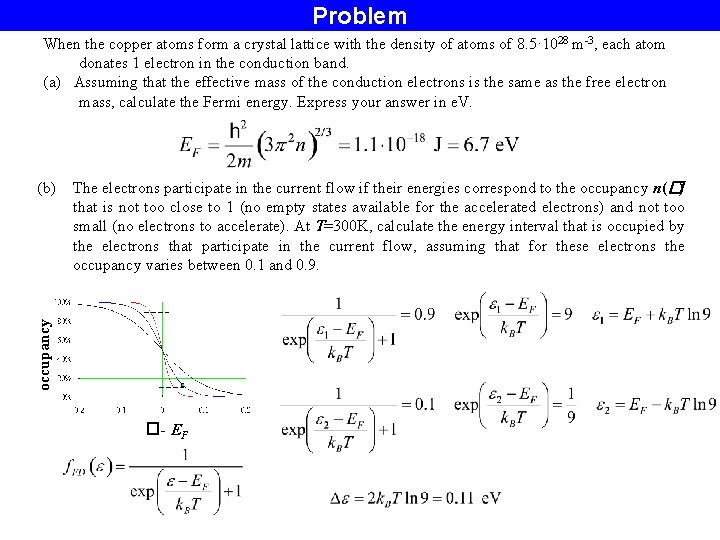
Problem When the copper atoms form a crystal lattice with the density of atoms of 8. 5· 1028 m-3, each atom donates 1 electron in the conduction band. (a) Assuming that the effective mass of the conduction electrons is the same as the free electron mass, calculate the Fermi energy. Express your answer in e. V. The electrons participate in the current flow if their energies correspond to the occupancy n(�) that is not too close to 1 (no empty states available for the accelerated electrons) and not too small (no electrons to accelerate). At T=300 K, calculate the energy interval that is occupied by the electrons that participate in the current flow, assuming that for these electrons the occupancy varies between 0. 1 and 0. 9. occupancy (b) � - EF

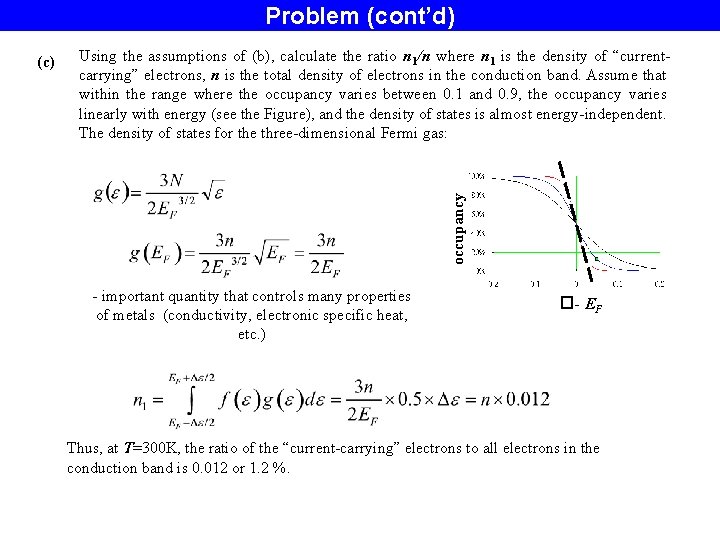
Problem (cont’d) Using the assumptions of (b), calculate the ratio n 1/n where n 1 is the density of “currentcarrying” electrons, n is the total density of electrons in the conduction band. Assume that within the range where the occupancy varies between 0. 1 and 0. 9, the occupancy varies linearly with energy (see the Figure), and the density of states is almost energy-independent. The density of states for the three-dimensional Fermi gas: occupancy (b) (c) - important quantity that controls many properties of metals (conductivity, electronic specific heat, etc. ) � - EF Thus, at T=300 K, the ratio of the “current-carrying” electrons to all electrons in the conduction band is 0. 012 or 1. 2 %.

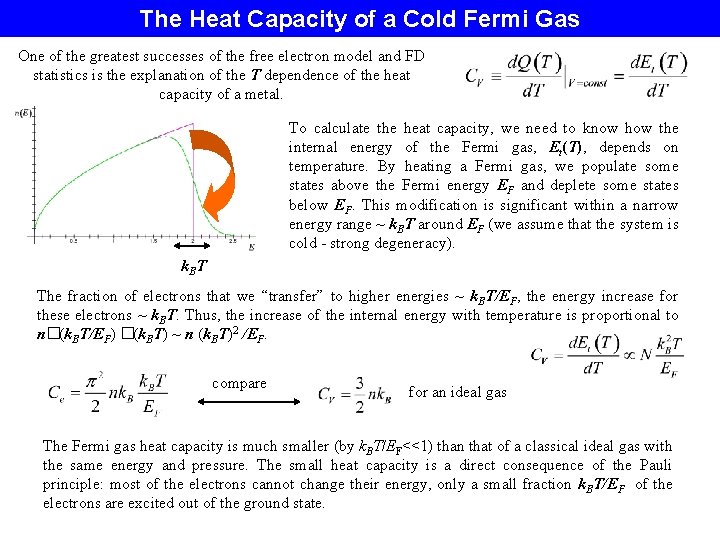
The Heat Capacity of a Cold Fermi Gas One of the greatest successes of the free electron model and FD statistics is the explanation of the T dependence of the heat capacity of a metal. To calculate the heat capacity, we need to know how the internal energy of the Fermi gas, Et(T), depends on temperature. By heating a Fermi gas, we populate some states above the Fermi energy EF and deplete some states below EF. This modification is significant within a narrow energy range ~ k. BT around EF (we assume that the system is cold - strong degeneracy). k. BT The fraction of electrons that we “transfer” to higher energies ~ k. BT/EF, the energy increase for these electrons ~ k. BT. Thus, the increase of the internal energy with temperature is proportional to n�(k. BT/EF) �(k. BT) ~ n (k. BT)2 /EF. compare for an ideal gas The Fermi gas heat capacity is much smaller (by k. BT/EF<<1) than that of a classical ideal gas with the same energy and pressure. The small heat capacity is a direct consequence of the Pauli principle: most of the electrons cannot change their energy, only a small fraction k. BT/EF of the electrons are excited out of the ground state.

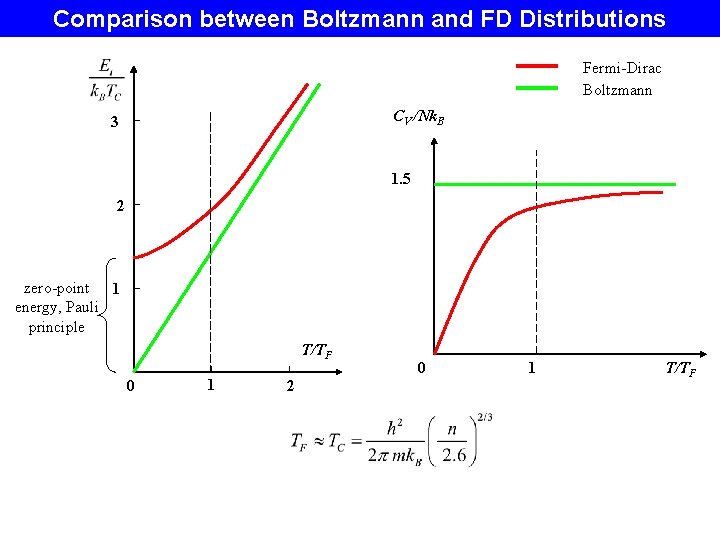
Comparison between Boltzmann and FD Distributions Fermi-Dirac Boltzmann CV /Nk. B 3 1. 5 2 zero-point 1 energy, Pauli principle T/TF 0 1 2 0 1 T/TF