Deflection Virtual Work Method Trusses Theory of Structure

Deflection: Virtual Work Method; Trusses Theory of Structure - I

Contents l l External Work and Strain Energy Principle of Work and Energy Principle of Virtual Work Method of Virtual Work: l Trusses 2

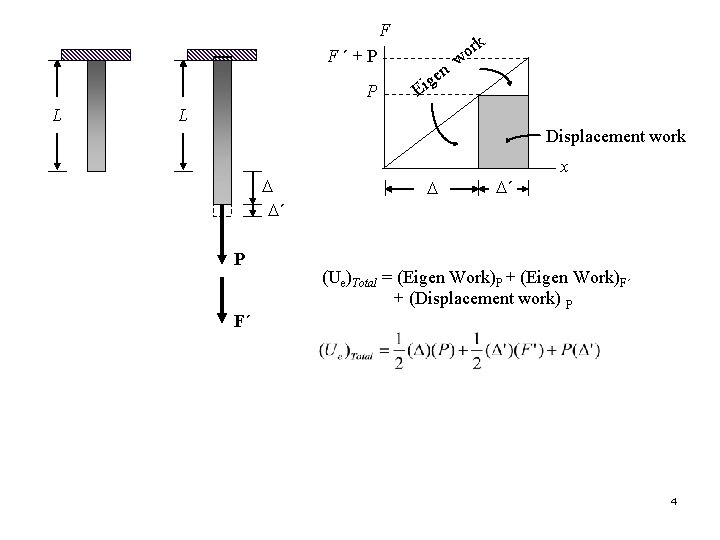
External Work and Strain Energy Most energy methods are based on the conservation of energy principle, which states that the work done by all the external forces acting on a structure, Ue, is transformed into internal work or strain energy, Ui. • External Work-Force. Ue = Ui F P Eigen work L Ue D D x As the magnitude of F is gradually increased from zero to some limiting value F = P, the final elongation of the bar becomes D. Eigen work F 3

F F´+P P L k n ge i E r wo L Displacement work D D´ P F´ D D´ x (Ue)Total = (Eigen Work)P + (Eigen Work)F´ + (Displacement work) P 4

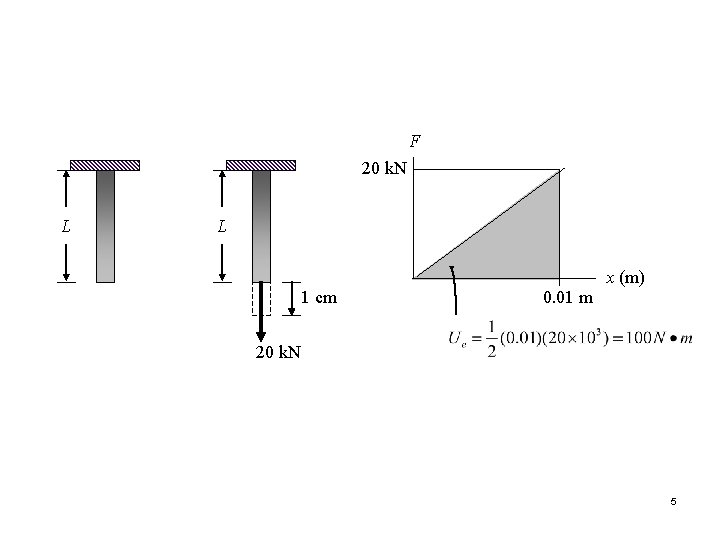
F 20 k. N L L 1 cm 0. 01 m x (m) 20 k. N 5

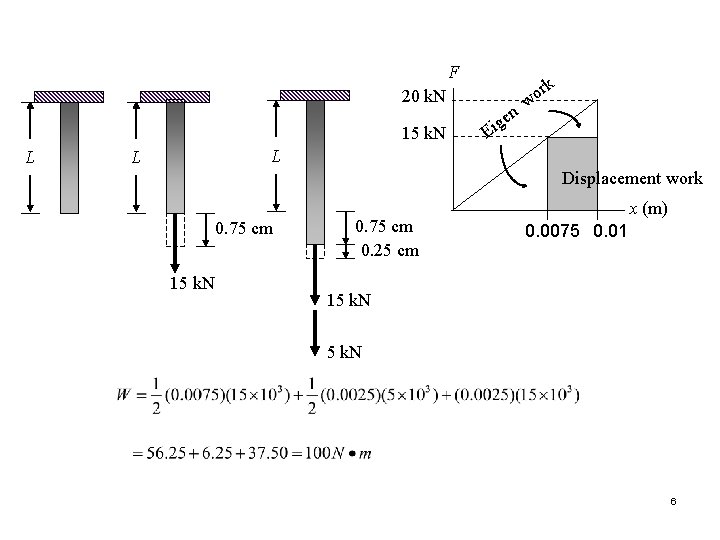
F 20 k. N 15 k. N L n ge i E rk o w L L Displacement work 0. 75 cm 15 k. N 0. 75 cm 0. 25 cm x (m) 0. 0075 0. 01 15 k. N 6

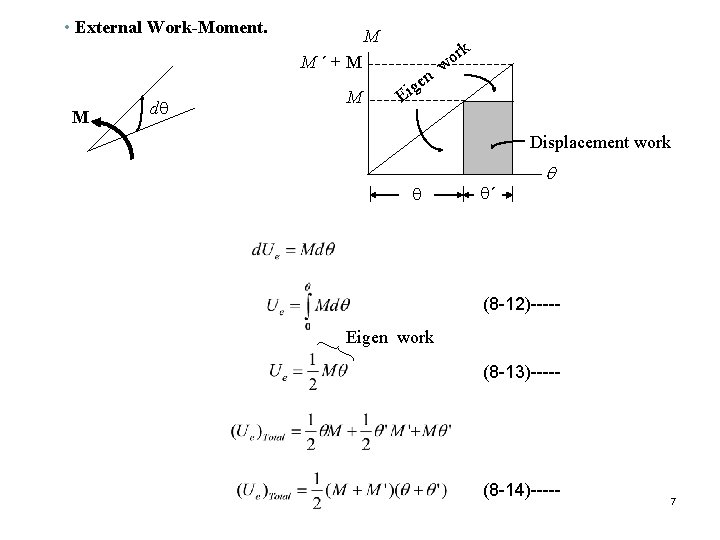
• External Work-Moment. M M´+M M dq M k n ge i E r wo Displacement work q q´ q (8 -12)----Eigen work (8 -13)----- (8 -14)----- 7

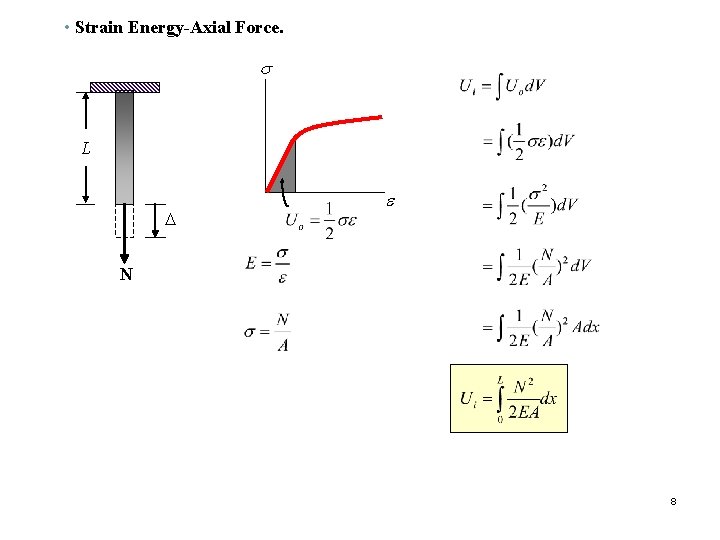
• Strain Energy-Axial Force. s L D e N 8

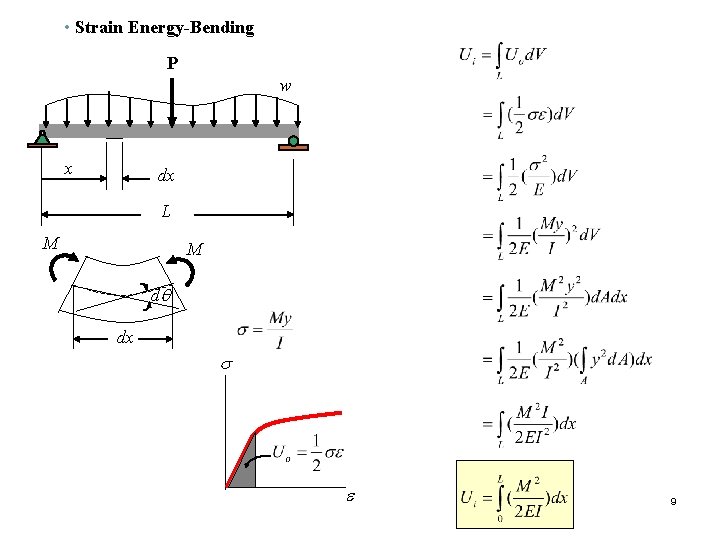
• Strain Energy-Bending P w x dx L M M dq dx s e 9

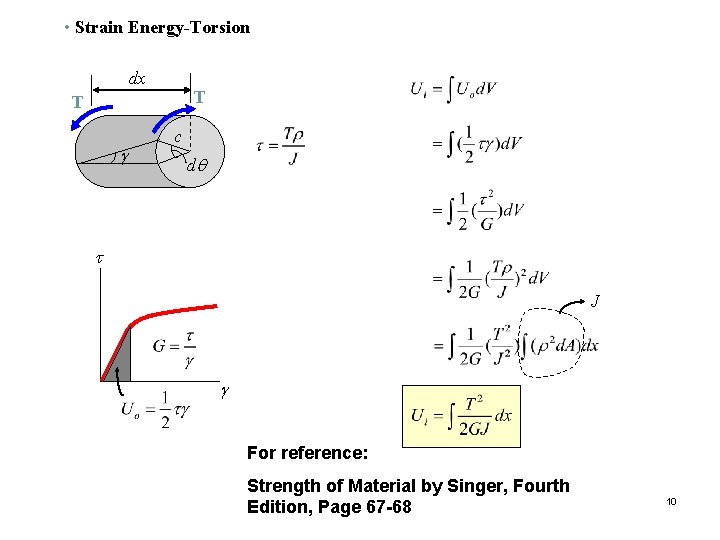
• Strain Energy-Torsion dx T T g c dq t J g For reference: Strength of Material by Singer, Fourth Edition, Page 67 -68 10

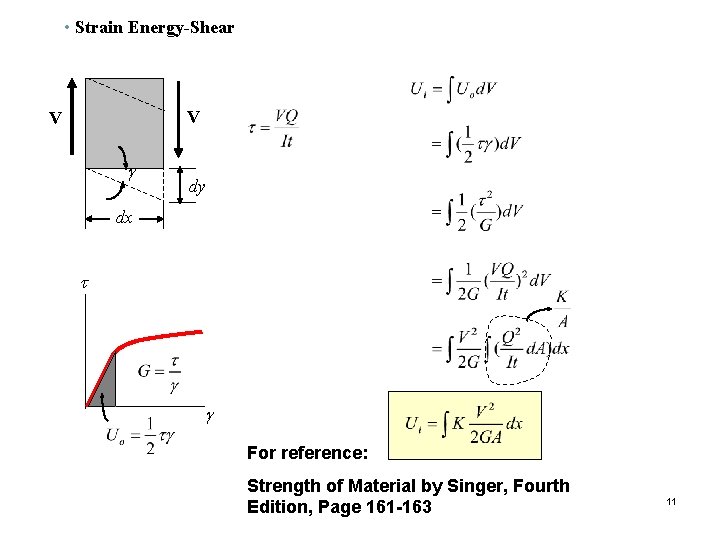
• Strain Energy-Shear V V g dy dx t g For reference: Strength of Material by Singer, Fourth Edition, Page 161 -163 11

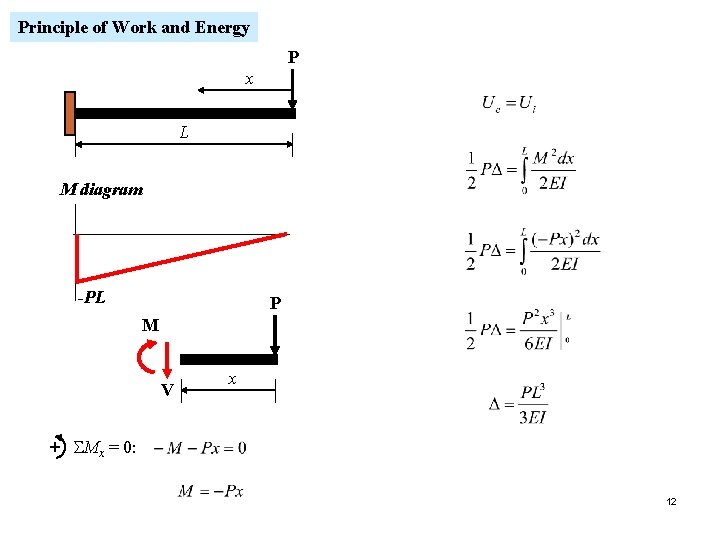
Principle of Work and Energy P x L M diagram -PL P M V x + SMx = 0: 12

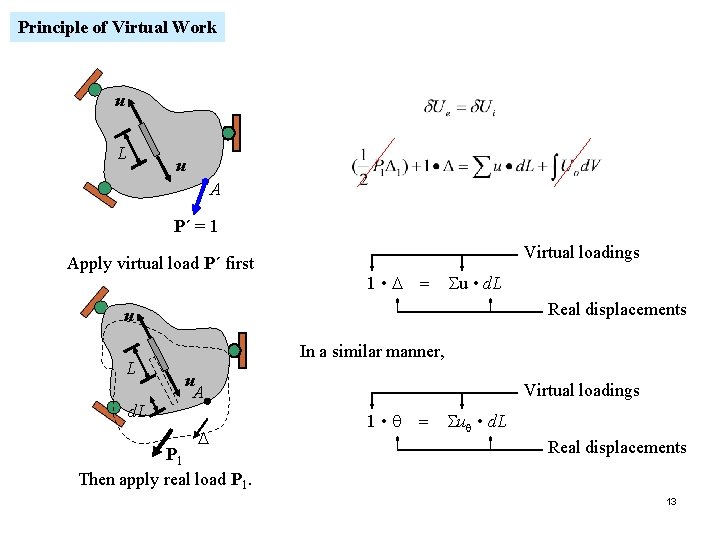
Principle of Virtual Work u L u A P´ = 1 Apply virtual load P´ first Virtual loadings 1 • D = Su • d. L Real displacements u L d. L In a similar manner, u A D P 1 Then apply real load P 1. Virtual loadings 1 • q = Suq • d. L Real displacements 13

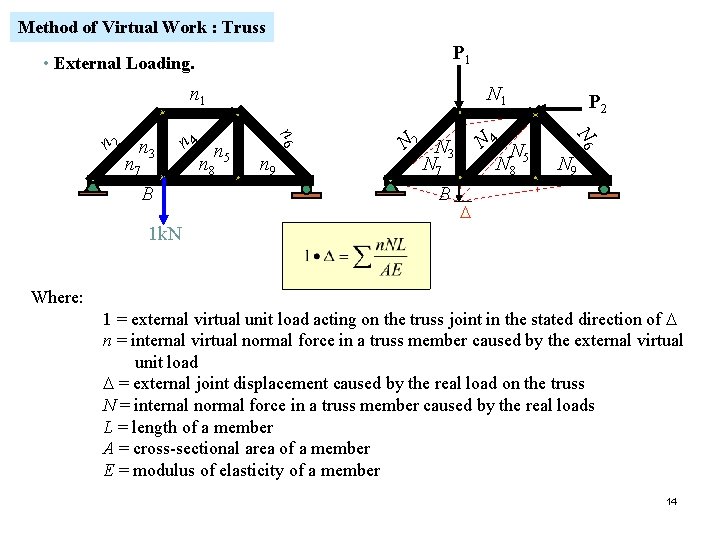
Method of Virtual Work : Truss P 1 • External Loading. n 8 n 9 4 N 3 N 7 B N 2 N 4 n n n 7 B n 5 N N 8 5 P 2 N 6 n 3 N 1 n 6 2 n 1 N 9 D 1 k. N Where: 1 = external virtual unit load acting on the truss joint in the stated direction of D n = internal virtual normal force in a truss member caused by the external virtual unit load D = external joint displacement caused by the real load on the truss N = internal normal force in a truss member caused by the real loads L = length of a member A = cross-sectional area of a member E = modulus of elasticity of a member 14

• Temperature Where: D = external joint displacement caused by the temperature change a = coefficient of thermal expansion of member DT = change in temperature of member • Fabrication Errors and Camber Where: D = external joint displacement caused by the fabrication errors DL = difference in length of the member from its intended size as 15 caused by a fabrication error

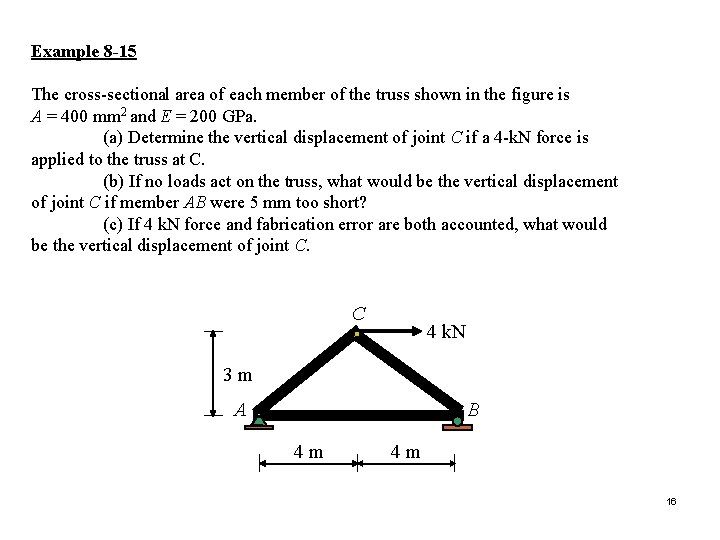
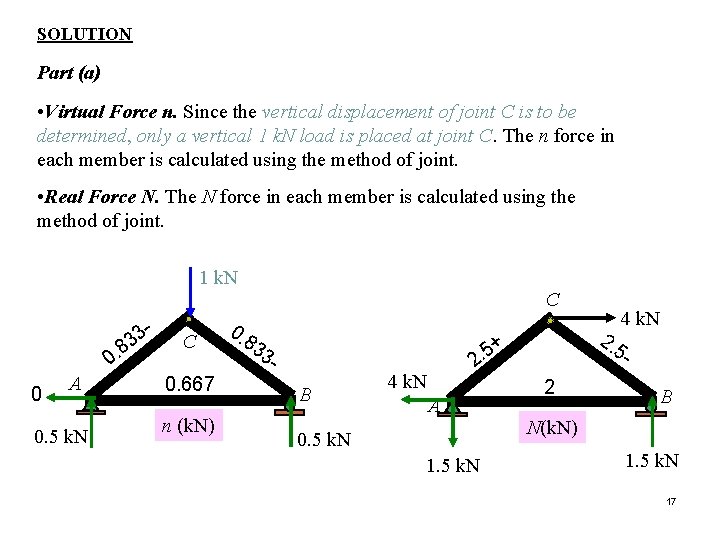
Example 8 -15 The cross-sectional area of each member of the truss shown in the figure is A = 400 mm 2 and E = 200 GPa. (a) Determine the vertical displacement of joint C if a 4 -k. N force is applied to the truss at C. (b) If no loads act on the truss, what would be the vertical displacement of joint C if member AB were 5 mm too short? (c) If 4 k. N force and fabrication error are both accounted, what would be the vertical displacement of joint C. C 4 k. N 3 m A B 4 m 4 m 16

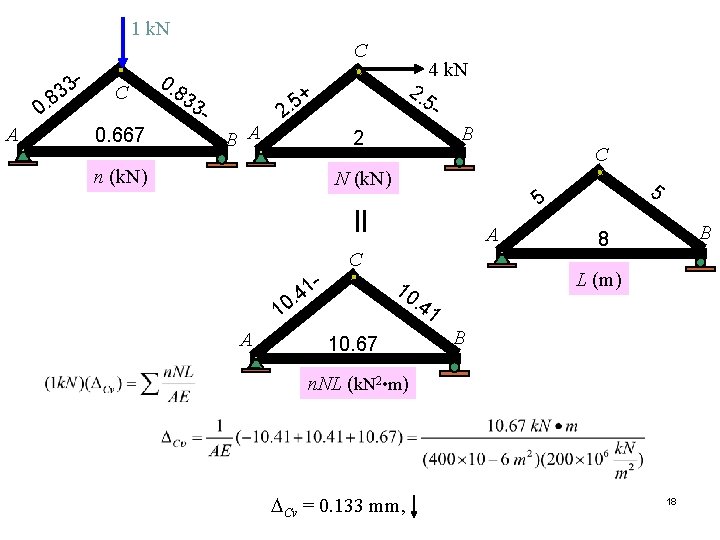
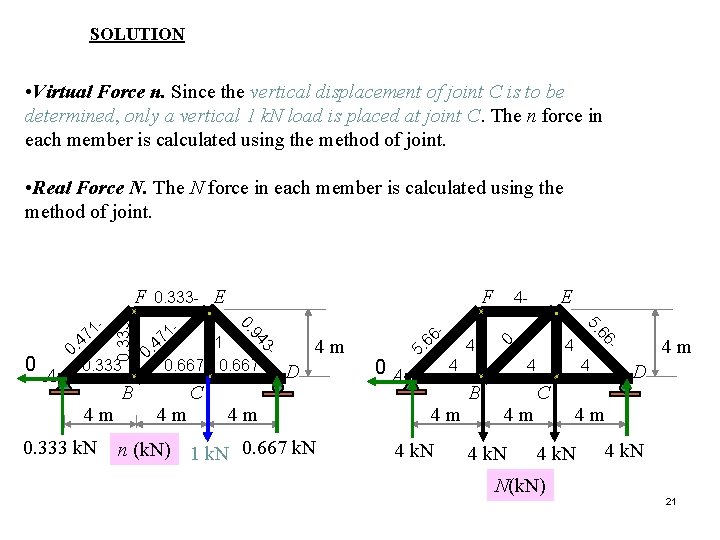
SOLUTION Part (a) • Virtual Force n. Since the vertical displacement of joint C is to be determined, only a vertical 1 k. N load is placed at joint C. The n force in each member is calculated using the method of joint. • Real Force N. The N force in each member is calculated using the method of joint. 1 k. N 3 - 83. 0 0 A 0. 5 k. N C 0. 667 n (k. N) 0. C 83 3 B 5 2. 4 k. N A + 2 4 k. N 2. 5 B N(k. N) 0. 5 k. N 17

1 k. N 3 - 0 A 3. 8 C 0. 667 0. C 83 3 B A 5 2. 4 k. N 2. 5 - + B 2 n (k. N) C N (k. N) = 1 4 A A C 10 5 5 L (m) . 4 10. 67 B 8 1 B n. NL (k. N 2 • m) DCv = 0. 133 mm, 18

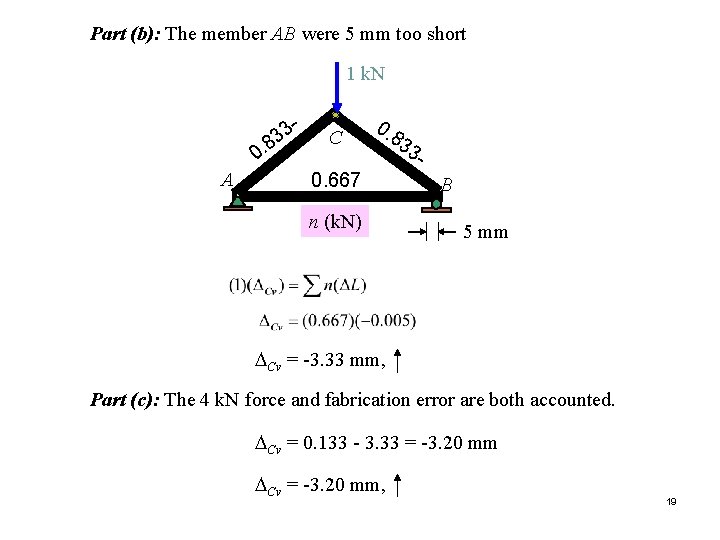
Part (b): The member AB were 5 mm too short 1 k. N 33 8 0. A C 0. 667 n (k. N) 83 3 B 5 mm DCv = -3. 33 mm, Part (c): The 4 k. N force and fabrication error are both accounted. DCv = 0. 133 - 3. 33 = -3. 20 mm DCv = -3. 20 mm, 19

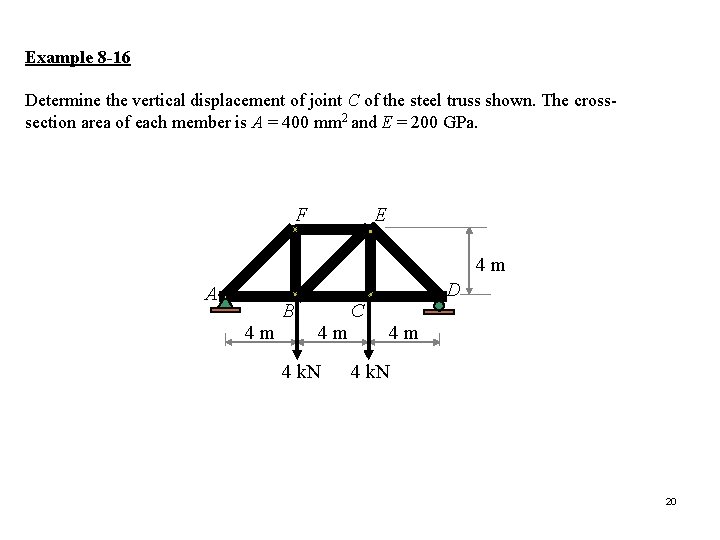
Example 8 -16 Determine the vertical displacement of joint C of the steel truss shown. The crosssection area of each member is A = 400 mm 2 and E = 200 GPa. F E 4 m A B 4 m D C 4 m 4 k. N 20

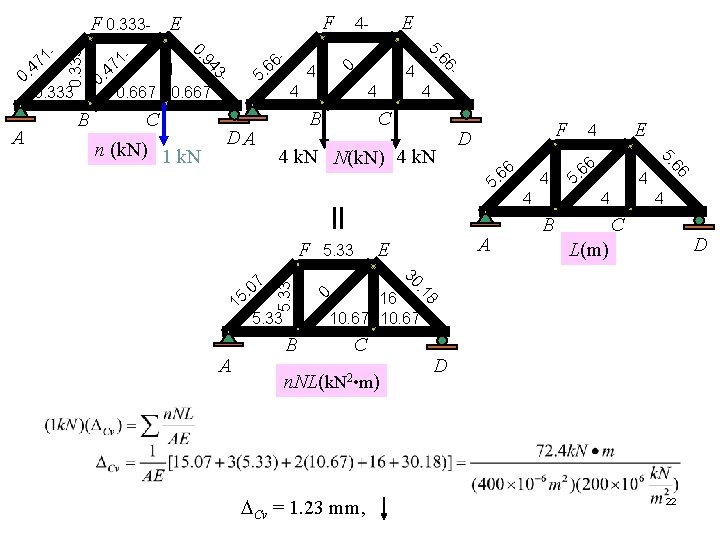
SOLUTION • Virtual Force n. Since the vertical displacement of joint C is to be determined, only a vertical 1 k. N load is placed at joint C. The n force in each member is calculated using the method of joint. • Real Force N. The N force in each member is calculated using the method of joint. 4 m 0. 333 k. N C 4 m D 4 m n (k. N) 1 k. N 0. 667 k. N 0 A 5 0 4 4 B 4 m 4 k. N 4 D C 4 m 4 k. N 4 m - B 4 m - 66 1 0. 667 6. 6 E 4 - 5. 0. 333 - F 3 - A 0. 1 47 E 94 0 0. 333 - 0. 17 4 0. 333 F 4 m 4 k. N N(k. N) 21

F F 0. 333 - E 4 4 4 B 4 C 6 5. = F B 4 4 B 4 C D L(m) 0 16 10. 67 C n. NL(k. N 2 • m) DCv = 1. 23 mm, 8 A 5. 33 4 6 6 5. . 1 1 4 30 07. 5 A E 5. 33 6 E 4 66 4 k. N N(k. N) 4 k. N F D 5. n (k. N) 1 k. N DA 0 4 5. 33 0. 333 5 - C - 66 5. 6. 6 3 - A B 17 1 4 0. 0. 667 94 0. 17 4 0. 0. 333 E 4 - D 22

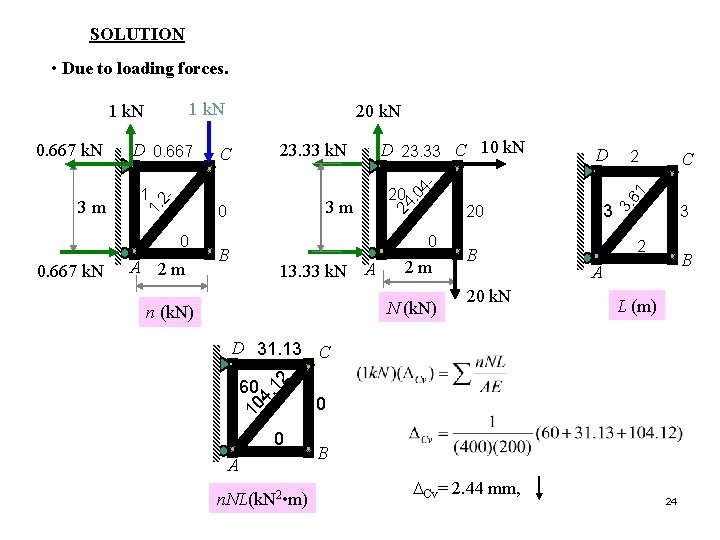
Example 8 -17 Determine the vertical displacement of joint C of the steel truss shown. Due to radiant heating from the wall, members are subjected to a temperature change: member AD is increase +60 o. C, member DC is increase +40 o. C and member AC is decrease -20 o. C. Also member DC is fabricated 2 mm too short and member AC 3 mm too long. Take a = 12(10 -6) , the cross-section area of each member is A = 400 mm 2 and E = 200 GPa. wall C 10 k. N D 3 m B A 2 m 20 k. N 23

SOLUTION • Due to loading forces. 1 k. N A 2 m 20 0 B 13. 33 k. N A 2 m N (k. N) n (k. N) 2 B 20 k. N 3 C 61 20 D 4 - D 23. 33 C 10 k. N 3 3. 3 m 0 0 2 B A L (m) 60 12 D 31. 13 C 10 4. 0. 667 k. N 23. 33 k. N C . 0 1 2 - 3 m D 0. 667 1. 0. 667 k. N 20 k. N 24 1 k. N 0 A n. NL(k. N 2 • m) 0 B DCv= 2. 44 mm, 24

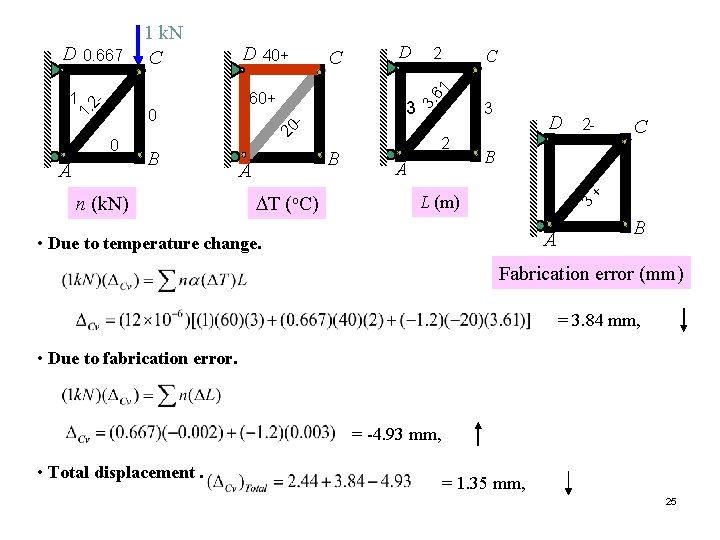
D B n (k. N) 2 1 C 3. 6 60+ 3 3 D B A DT (o. C) 2 A 2 - C B + A C L (m) 3 0 40+ 20 0 D - 1. 2 1 0. 667 - D 1 k. N C A • Due to temperature change. B Fabrication error (mm) = 3. 84 mm, • Due to fabrication error. = -4. 93 mm, • Total displacement. = 1. 35 mm, 25

26