Definitions Translation shifts a graph horizontally andor vertically

Definitions �Translation: shifts a graph horizontally and/or vertically, but does not change its size, shape, or orientation. �Reflection: when a= -1. �Y = a x- h + k ; where a = slope, (h, k) is vertex

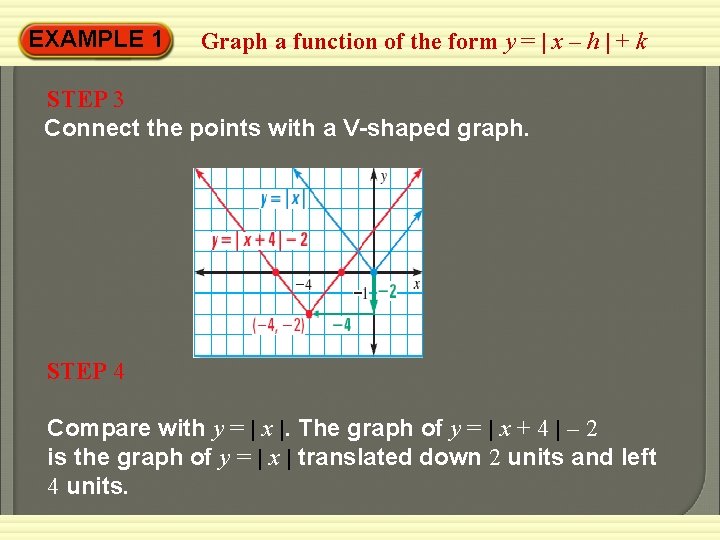
EXAMPLE 1 Graph a function of the form y = | x – h | + k Graph y = | x + 4 | – 2. Compare the graph with the graph of y = | x |. SOLUTION STEP 1 Identify and plot the vertex, (h, k) = (– 4, – 2). STEP 2 Plot another point on the graph, such as (– 2, 0). Use symmetry to plot a third point, (– 6, 0).

EXAMPLE 1 Graph a function of the form y = | x – h | + k STEP 3 Connect the points with a V-shaped graph. STEP 4 Compare with y = | x |. The graph of y = | x + 4 | – 2 is the graph of y = | x | translated down 2 units and left 4 units.

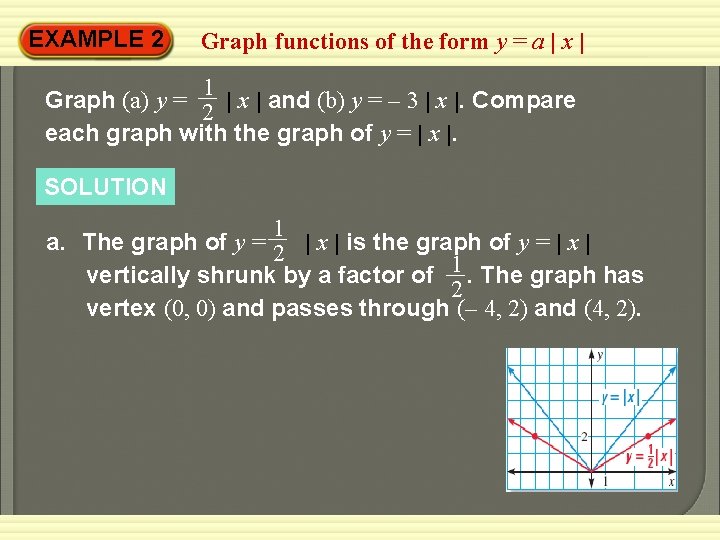
EXAMPLE 2 Graph functions of the form y = a | x | 1 Graph (a) y = | x | and (b) y = – 3 | x |. Compare 2 each graph with the graph of y = | x |. SOLUTION 1 a. The graph of y = 2 | x | is the graph of y = | x | vertically shrunk by a factor of 1. The graph has 2 vertex (0, 0) and passes through (– 4, 2) and (4, 2).

EXAMPLE 2 Graph functions of the form y = a | x | b. The graph of y = – 3 | x | is the graph of y = | x | vertically stretched by a factor of 3 and then reflected in the x-axis. The graph has vertex (0, 0) and passes through (– 1, – 3) and (1, – 3).

EXAMPLE 3 Graph a function of the form y = a x – h + k Graph y = – 2 x – 1 + 3. Compare the graph with the graph of y = x. SOLUTION STEP 1 Identify and plot the vertex, (h, k) = (1, 3). STEP 2 Plot another point on the graph, such as (0, 1). Use symmetry to plot a third point, (2, 1).

EXAMPLE 3 Graph a function of the form y = a x – h + k STEP 3 Connect the points with a V-shaped graph. STEP 4 Compare with y = x. The graph of y = – 2 x – 1 + 3 is the graph of y = x stretched vertically by a factor of 2, then reflected in the x-axis, and finally translated right 1 unit and up 3 units.

GUIDED PRACTICE for Examples 1, 2 and 3 Graph the function. Compare the graph with the graph of y = |x|. 1. y = |x – 2| + 5 SOLUTION STEP 1 Identify and plot the vertex, (h, k) = (– 2, 5). STEP 2 Plot another point on the graph, such as (5, 0). Use symmetry to plot a third point, (7, 5).

GUIDED PRACTICE for Examples 1, 2 and 3 Connect the points with a V-shaped graph. STEP 4 Compare with y = | x |. The graph of y = |x – 2| + 5 is the graph of y = | x | translated right 2 units and up 5 units. SOLUTION The graph is translated right 2 units and up 5 units

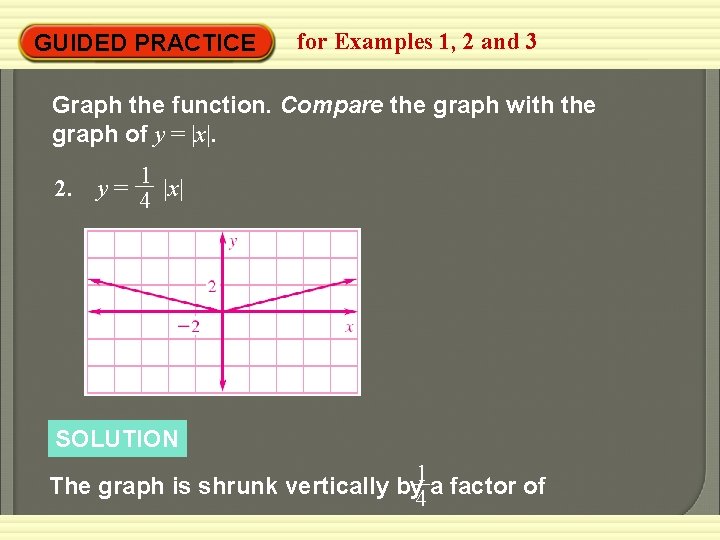
GUIDED PRACTICE for Examples 1, 2 and 3 Graph the function. Compare the graph with the graph of y = |x|. 1 2. y = 4 |x| SOLUTION 1 The graph is shrunk vertically by 4 a factor of

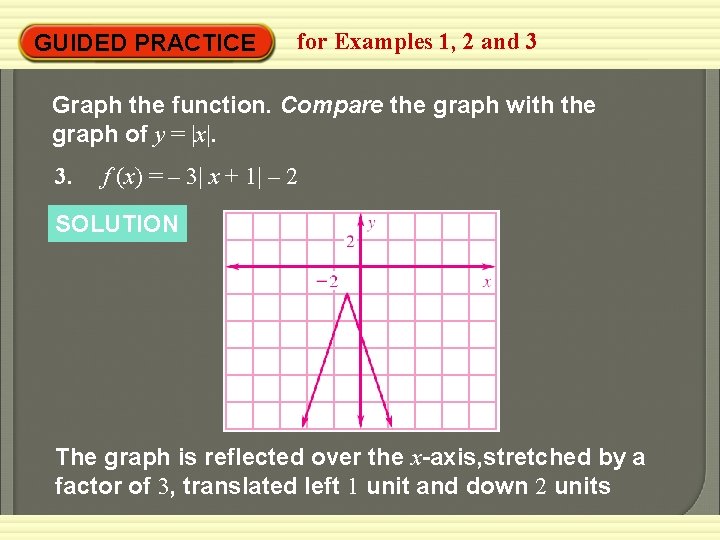
GUIDED PRACTICE for Examples 1, 2 and 3 Graph the function. Compare the graph with the graph of y = |x|. 3. f (x) = – 3| x + 1| – 2 SOLUTION The graph is reflected over the x-axis, stretched by a factor of 3, translated left 1 unit and down 2 units