Definition of Trace Function n Trace function Trace

Definition of Trace Function n Trace function 定義如下:

Trace Function examples

(Generalized)Definition of WG transform Input: Output: 假設 Trace表示法為 即為 WG-Transform結果 , 其中 之

WG transform example 經過WG-Transform後得到

(Generalized)Definition of WG sequence Input: {a} a binary sequence, period Output: {b} a binary sequence, period 將{a}以Trace表示, 找到其相對應的產生function I. e: 則將 作WG Transform得到之 依序求出 則{b}稱為{a}的WG Transform Sequence

WG transform sequence example {a}={0111111} 對應的產生函數為 經過WG-Transform {b}={1000000}

WG transform special case 雖然WG-Transform定義域為 但目前僅發現於 n=3 k-1時: n=3 k-2時: 轉換所得之 所產生的sequence具備 2 -level autocorrelation性質

WG transform special case n 因為只有此特殊形式的f(x)=Tr(g(x))經過WGTransform會產生autocorrlelation, 所以之後的 討論均僅針對此形式經過WG-Transform後所 得的 , 談論以下性質 n n 所產生sequence的autocorrelation特性 對應Boolean Function的Nonlinearlity 對應Boolean Function的CI 對應Boolean Function的algebraic degree

Definition of Hadamard Transform n 對於 Transform定義如下: 的Hadamard

Hadamard Transform example

Hadamard Transform example (cont. )

Hadamard Transform example (cont. )

Hadamard Transform of WG-transform n 討論特殊g(x)型態下, WG-Transform後的結果 進行Hadamard Transform, 其值如下: By [Multiplicative difference sets via additive characters] DILLON 99

Definition of Hadamard Transform Boolean function version n 特殊g(x)型態下, WG-Transform後的結果 當中的 x 改以一組基底的線性 組合來表示, 則展開化簡後形成一Boolean Function Example: (此處以較簡單的g(x)展示)

Hadamard Transform Boolean function version example 取標準基底 , 則

Hadamard Transform of polynomial form and Walsh Transform of Boolean form n 參數關係如下: 一定找的到對應的參數

Example

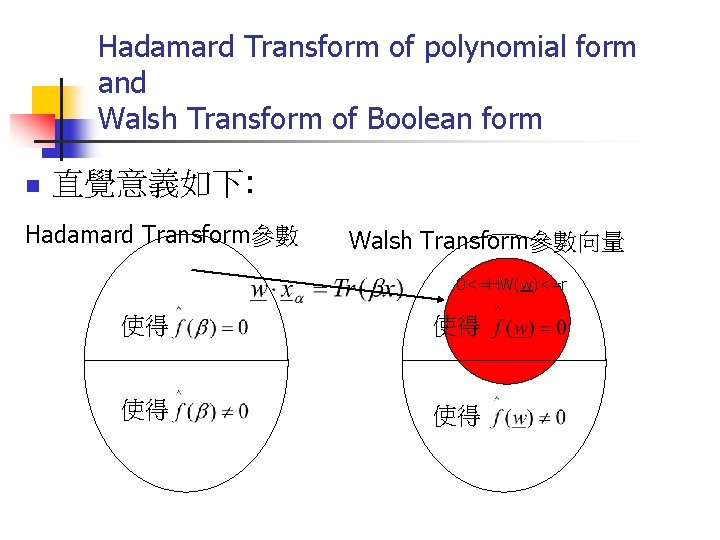
Hadamard Transform of polynomial form and Walsh Transform of Boolean form n 直覺意義如下: Hadamard Transform參數 Walsh Transform參數向量 0<=HW(w)<=r 使得 使得

r-Resilient of Boolean form WG-Transform n f(x) is r-order correlation immune if n Recall that Let And Theorem f(x) is r-resilient n , be a basis of over

1 -Resilient of Boolean form WG-Transform Theorem 設基底為 收集n個 集合中線性獨立向量 寫作A矩陣之列向量, 則取新基底如下, 則依此新基底所產 生之Boolean Function具有1 -order correlation immune n

1 -Resilient of Boolean form WG-Transform n Pf:

WG’s Boolean version CI order upper bound n Theorem: WG-transform Boolean version with CI order upper bound Pf: