Definition of Sine and Cosine Revisited Suppose P

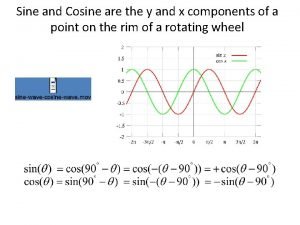
Definition of Sine and Cosine Revisited • Suppose P = (x, y) is the point on the unit circle specified by the angle. We define the functions, cosine of , or , and the sine of , or , by either pair of formulas: (-1, 0) Hypotenuse Side Adjacent Side Opposite

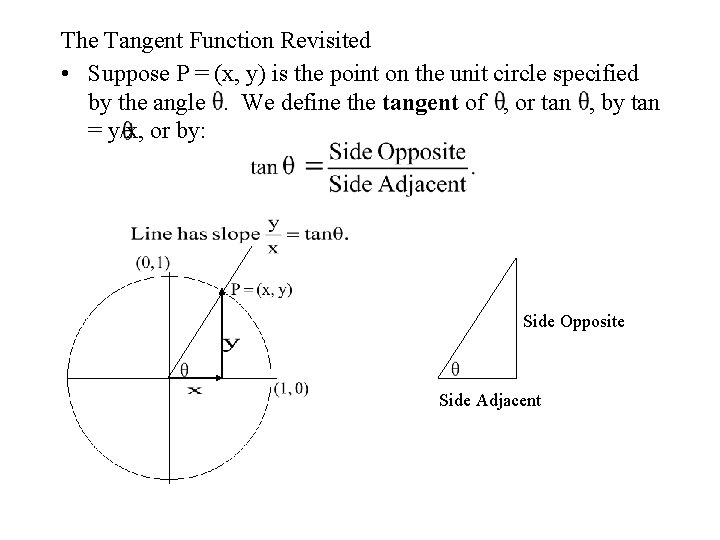
The Tangent Function Revisited • Suppose P = (x, y) is the point on the unit circle specified by the angle. We define the tangent of , or tan , by tan = y/x, or by: Side Opposite Side Adjacent

Solving Right Triangles • One of the angles of a right triangle is 90°. Thus, one part is already known and the only additional information necessary is either two sides or an acute angle and a side. With this additional information, it is possible to solve for the remaining parts. • Making a carefully labeled sketch of the triangle is important in solving these problems. • Problem 8, page 292. The top of a 200 -foot tower is to be anchored by cables that make an angle of 30° with the ground. How long must the cables be? How far from the base of the tower should the anchors be placed? h 200 ft 30° x sin 30° = 200/h => h = 200/sin 30° = 400 ft tan 30° = 200/x => x = 200/tan 30° = 346. 4 ft

Solving Non-right Triangles • Suppose the triangle to be solved does not contain a right angle. If we are given three parts of the triangle, not all angles, then we can solve for the remaining parts. The solution exists and is unique except in one case--discussed in a later slide. • Usually we label the angles of the triangle as A, B, C and the sides opposite these angles as a, b, and c, respectively. b A • Law of Cosines: • Law of Sines: C c a B

An example using the Law of Cosines • A person leaves her home and walks 5 miles due east and then 3 miles northeast. How far away from home (as the crow flies) is she? As seen from her home, what is the angle between the easterly direction and the direction to her destination? Destination N x Home 5 3 135° 45° • By applying the Law of Cosines, we can solve for x: • A second application of the Law of Cosines gives:

An example using the Law of Sines • Problem 21, page 298. Two fire stations are located 567 feet apart, at points A and B. There is a forest fire at point C. If CAB = 54° and CBA = 58°, which fire station is closer? How much closer? C b 68° a 58° B A 54° c = 567 ft • The fire station at point B is closer to the fire by 518. 61 – 494. 74 = 23. 87 feet.

The ambiguous case for solving a triangle • Suppose we are given two sides of a triangle and the angle opposite one of them, and we are asked to find the remaining parts of the triangle. Depending on the data given, there may be: two possible triangles, one possible triangle, or no possible triangle. • Example. CAB = 45°, b = 1, and various values of a: C a=3/10 b=1 45° A No triangle exists. C b=1 45° A C a= 2/2 One triangle exists. B C b=1 45° A a=8/10 Two triangles exist. b=1 45° A a=11/10 B

Summary for Trigonometry • Sine, cosine, and tangent were redefined in terms of right triangles. • Right triangles in which either two sides or an acute angle and a side are given can be solved. • We may consider solving non-right triangles in which three parts, not all angles, are given. The solution exists and is unique except in the ambiguous case when two sides and the angle opposite one of them are given. • In the ambiguous case, there may be: two possible triangles, one possible triangle, or no possible triangle. • The law of cosines is a generalization of the Pythagorean theorem that works for any triangle. • The law of sines is useful when we know a side and the angle opposite it.