Definition of Computer Science is the science of

Definition of Computer Science is the science of algorithmic problem solving. Their formal and mathematical properties Studying the behavior of algorithms to determine whether they are correct and efficient. Their hardware realizations Designing and building computer systems that are able to execute algorithms Their linguistic realizations Designing programming languages and translating algorithms into these languages so that they can be executed by hardware Their applications Identifying important problems and designing correct and efficient software packages to solve these problems.

Algorithms Step-by-step instructions that tell a computing agent how to solve some problem using only finite resources Resources Memory CPU cycles Time/Space Types of instructions Sequential Conditional If statements Iterative Loops 3

Pseudocode: The Interlingua for Algorithms an English-like description of the sequential, conditional, and iterative operations of an algorithm no rigid syntax. As with an essay, clarity and organization are key. So is completeness. 4

Pseudocode Example Find Largest Number Input: A list of positive numbers Output: The largest number in the list Procedure: 1. Set Largest to zero 2. Set Current-Number to the first in the list 3. While there are more numbers in the list 3. 1 if (the Current-Number > Largest) then 3. 1. 1 Set Largest to the Current-Number 3. 2 Set Current-Number to the next one in the list 4. Output Largest 5

Pseudocode Example Find Largest Number Input: A list of positive numbers Output: The largest number in the list Procedure: conditional 1. Set Largest to zero operation 2. Set Current-Number to the first in the list 3. While there are more numbers in the list 3. 1 if (the Current-Number > Largest) then 3. 1. 1 Set Largest to the Current-Number 3. 2 Set Current-Number to the next one in the list 4. Output Largest 6

Pseudocode Example Find Largest Number Input: A list of positive numbers Output: The largest number in the list iterative Procedure: operation 1. Set Largest to zero 2. Set Current-Number to the first in the list 3. While there are more numbers in the list 3. 1 if (the Current-Number > Largest) then 3. 1. 1 Set Largest to the Current-Number 3. 2 Set Current-Number to the next one in the list 4. Output Largest 7

Pseudocode Example Find Largest Number Input: A list of positive numbers Output: The largest number in the list Procedure: 1. Set Largest to zero 2. Set Current-Number to the first in the list 3. While there are more numbers in the list 3. 1 if (the Current-Number > Largest) then 3. 1. 1 Set Largest to the Current-Number 3. 2 Set Current-Number to the next one in the list 4. Output Largest Let’s “play computer” to review this algorithm… 8

Question How do we measure running time? Analysis of Algorithms 9

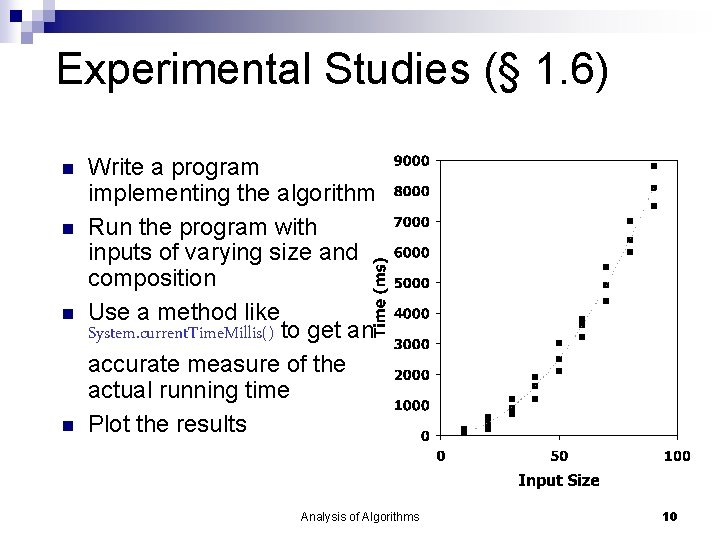
Experimental Studies (§ 1. 6) Write a program implementing the algorithm Run the program with inputs of varying size and composition Use a method like System. current. Time. Millis() to get an accurate measure of the actual running time Plot the results Analysis of Algorithms 10

Limitations of Experiments It is necessary to implement the algorithm, which may be difficult Results may not be indicative of the running time on other inputs not included in the experiment. In order to compare two algorithms, the same hardware and software environments must be used 11 Analysis of Algorithms

Question What is solution? Analysis of Algorithms 12

Primitive Operations 13 Basic computations performed by an algorithm Identifiable in pseudocode Largely independent from the programming language Exact definition not important (we will see why later) Assumed to take a constant amount of time in the RAM model Examples: Evaluating an expression Assigning a value to a variable Indexing into an array Calling a method Returning from a method Analysis of Algorithms

Counting Primitive Operations By inspecting the pseudocode, we can determine the maximum number of primitive operations executed by an algorithm, as a function of the input size Algorithm array. Max (A, n) # operations current. Max A[0] 2 for i 1 to n 1 do 2+n if A[i] current. Max then 2(n 1) current. Max A[i] 2(n 1) { increment counter i } 2(n 1) return current. Max 1 Total 7 n 1 14 Analysis of Algorithms

Estimating Running Time Algorithm array. Max executes 7 n 1 primitive operations in the worst case. Define: a = Time taken by the fastest primitive operation b = Time taken by the slowest primitive operation 15 Let T(n) be worst-case time of array. Max. Then a (7 n 1) T(n) b(7 n 1) Hence, the running time T(n) is bounded by two linear functions Analysis of Algorithms

Growth Rate of Running Time Changing the hardware/ software environment Affects T(n) by a constant factor, but Does not alter the growth rate of T(n) 16 The linear growth rate of the running time T(n) is an intrinsic property of algorithm array. Max Analysis of Algorithms

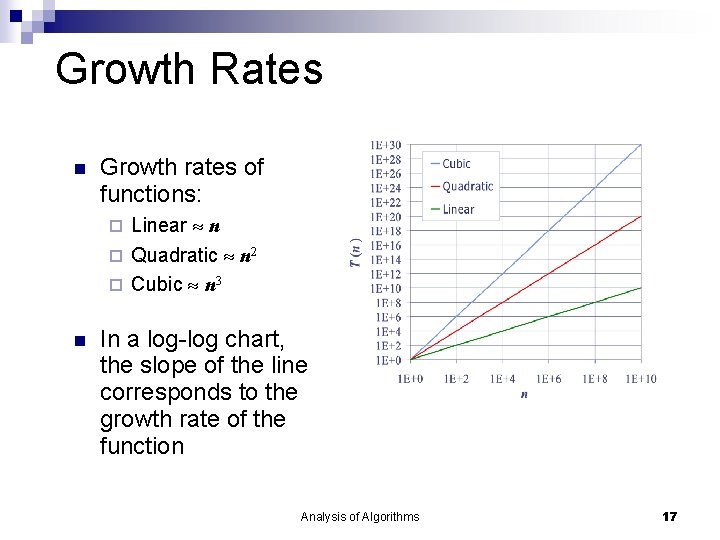
Growth Rates Growth rates of functions: Linear n Quadratic n 2 Cubic n 3 In a log-log chart, the slope of the line corresponds to the growth rate of the function Analysis of Algorithms 17

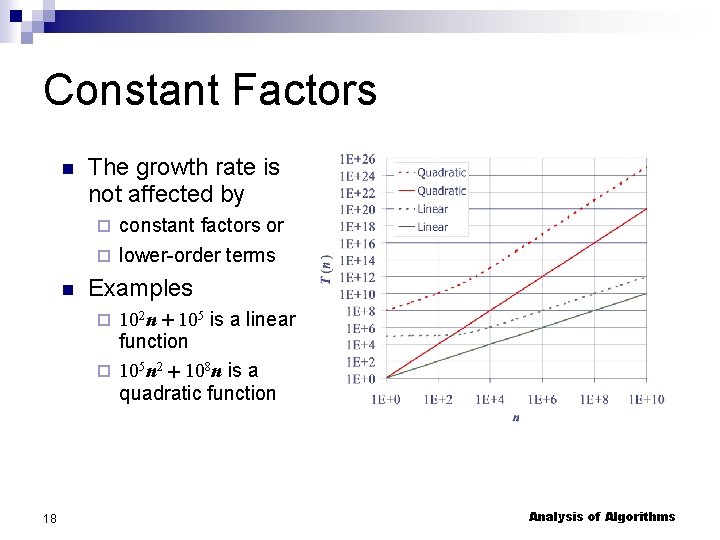
Constant Factors The growth rate is not affected by constant factors or lower-order terms Examples 102 n + 105 is a linear function 105 n 2 + 108 n is a quadratic function 18 Analysis of Algorithms

More Big-Oh Examples 7 n-2 is O(n) 3 n 3 + 20 n 2 + 5 is O(n 3) 3 log n + log log n is O(log n) 19 Analysis of Algorithms

Algorithms vary in efficiency example: sum the numbers from 1 to n Algorithm I 1. Set sum to 0 2. Set curr. Num to 1 3. Repeat until curr. Num > n 4. Set sum to sum + curr. Num 5. Set curr. Num to curr. Num + 1 efficiency space= 3 memory cells time = t(step 1) + +t(step 2) +. . . + +t(step n) • space requirement is constant (i. e. independent of n) • time requirement is linear (i. e. grows linearly with n) This is written “O(n)” to see this graphically. . . 20

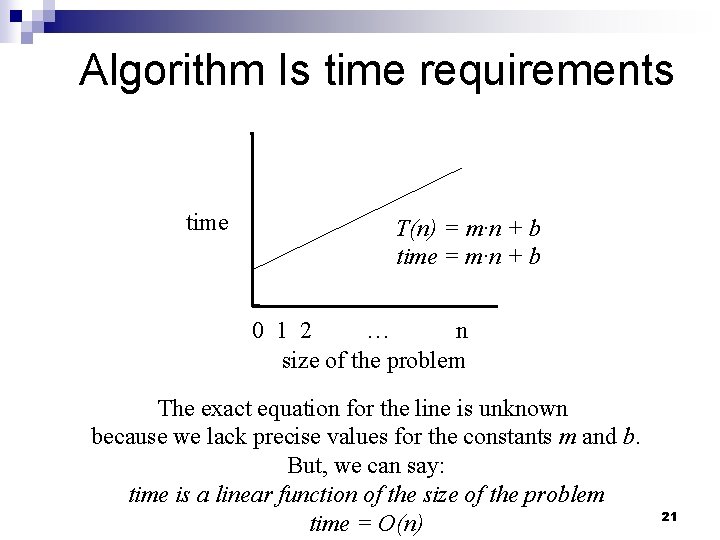
Algorithm Is time requirements time T(n) = m·n + b time = m·n + b 0 1 2 … n size of the problem The exact equation for the line is unknown because we lack precise values for the constants m and b. But, we can say: time is a linear function of the size of the problem time = O(n) 21

Algorithm II for summation First, consider a specific case: n = 100. The “key insight”, due to Gauss: the numbers can be grouped into 50 pairs of the form: 1 + 100 = 101 2 + 99 = 101 sum = 50 x 101. . . 50 + 51 = 101 } This algorithm requires a single multiplication! Second, generalize the formula for any n : sum = (n / 2) (n + 1) Time requirement is constant. time = O(1) 22

Sequential Search: A Commonly used Algorithm Suppose you want to a find a student in the TSU directory. It contains EIDs, names, phone numbers, lots of other information. You want a computer application for searching the directory: given an EID, return the student’s phone number. You want more, too, but this is a good start… 23

Sequential Search of a student database name 1 John Smith 2 Paula Jones 3 Led Belly . . . n Chuck Bin EID major JS 456 PJ 123 LEB 900 physics history . . . CB 1235 algorithm to search database by EID : music credit hrs. 36 125 72 . . . math 89 1. ask user to enter EID to search for 2. set i to 1 3. set found to ‘no’ 4. while i <= n and found = ‘no’ do 5. if EID = EIDi 6. then set found to ‘yes’ else 6. increment i by 1 7. if found = ‘no’ then print “no such student” 24 else < student found at array index i >

Time requirements for sequential search • best case (minimum amount of work): EID found in student 1 one loop iteration • worst case (maximum amount of work): EID found in studentn n loop iterations • average case (expected amount of work): EID found in studentn/2 loop iterations amount of work because the amount of work is a constant multiple of n, the time requirement is O(n) in the worst case and the average case. 25

O(n) searching is too slow Consider searching TSU’s student database using sequential search on a computer capable of 20, 000 integer comparisons per second: n = 150, 000 (students registered during past 15 years) average case 150, 000 2 comparisons x 1 seconds 20, 000 comparisons = 3. 75 seconds worst case 150, 000 comparisons x 1 seconds = 7. 5 seconds 20, 000 comparisons Bad news for searching NYC phone book, IRS database, 26. . .

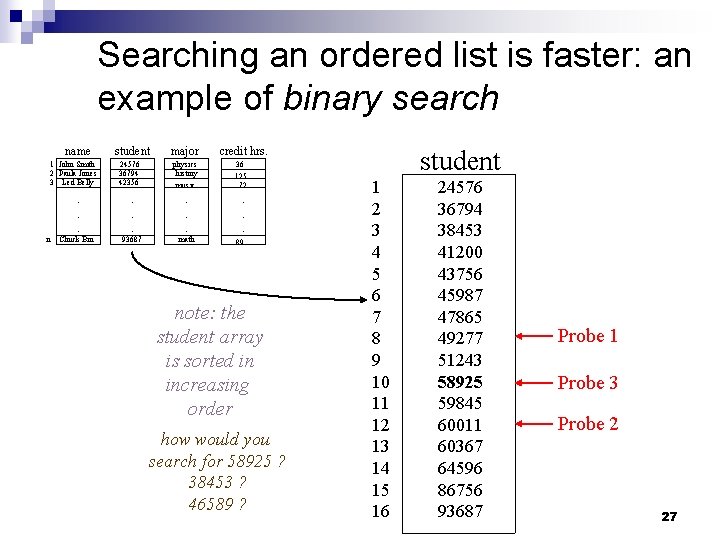
Searching an ordered list is faster: an example of binary search name 1 John Smith 2 Paula Jones 3 Led Belly n student 24576 36794 42356 major physics history music . . Chuck Bin 93687 math credit hrs. 36 125 72 . . . 89 note: the student array is sorted in increasing order how would you search for 58925 ? 38453 ? 46589 ? student 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 24576 36794 38453 41200 43756 45987 47865 49277 51243 58925 59845 60011 60367 64596 86756 93687 Probe 1 Probe 3 Probe 2 27

The binary search algorithm assuming that the entries in student are sorted in increasing order, 1. ask user to input student. Num to search for 2. set found to ‘no’ What does this mean? 3. while not done searching and found = ‘no’ 4. set middle to the index counter at the middle of the student list 5. if student. Num = studentmiddle then set found to ‘yes’ 6. if student. Num < studentmiddle then chop off the last half of the student list How? 7. If student. Num > studentmiddle then chop off the first half of the student list How? 8. if found = ‘no’ then print “no such student” else <student. Num found at array index middle> 28

The binary search algorithm assuming that the entries in student are sorted in increasing order, 1. ask user to input student. Num to search for 2. set beginning to 1 3. set end to n 4. set found to ‘no’ 5. while beginning <= end and found = ‘no’ 6. set middle to (beginning + end) / 2 {round down to nearest integer} 7. if student. Num = studentmiddle then set found to ‘yes’ 8. if student. Num < studentmiddle then set end to middle - 1 9. if student. Num > studentmiddle then set beginning to middle + 1 10. if found = ‘no’ then print “no such student” else <student. Num found at array index middle> 29

Time requirements for binary search At each iteration of the loop, the algorithm cuts the list (i. e. the list called student) in half. In the worst case (i. e. when student. Num is not in the list called student) how many times will this happen? n = 16 1 st iteration 16/2 = 8 2 nd iteration 8/2 = 4 3 rd iteration 4/2 = 2 4 th iteration 2/2 = 1 the number of times a number n can be cut in half and not go below 1 is log 2 n. Said another way: log 2 n = m is equivalent to 2 m = n In the average case and the worst case, binary search is O(log 2 n) 30

This is a major improvement n 100 150, 000 20, 000 sequential search O(n) binary search O(log 2 n) 100 150, 000 20, 000 7 18 25 number of comparisons needed in the worst case 27=128 218=262, 144 225 is about 33, 000 in terms of seconds. . . sequential search: vs. binary search: 150, 000 comparisons x 18 comparisons x 1 second = 7. 5 seconds 20, 000 comparisons 1 second >. 001 seconds 20, 000 comparisons 31

Conclusions Algorithms are the key to creating computing solutions. The design of an algorithm can make the difference between useful and impractical. Algorithms often have a trade-off between space (memory) and time. Efficient Algorithms allow to solve a problem faster thus wasting less electricity. 32

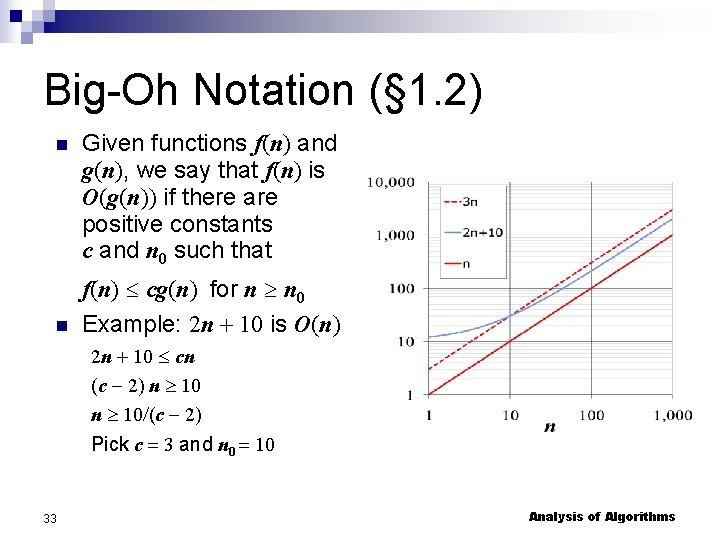
Big-Oh Notation (§ 1. 2) Given functions f(n) and g(n), we say that f(n) is O(g(n)) if there are positive constants c and n 0 such that f(n) cg(n) for n n 0 Example: 2 n + 10 is O(n) 2 n + 10 cn (c 2) n 10/(c 2) Pick c = 3 and n 0 = 10 33 Analysis of Algorithms

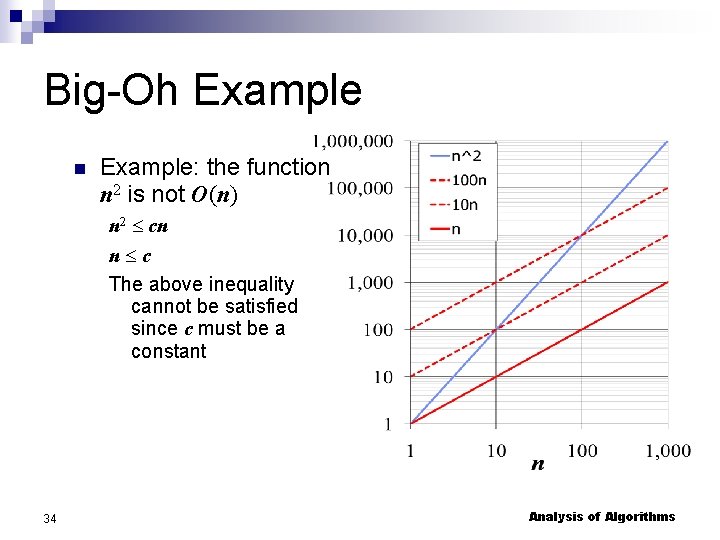
Big-Oh Example: the function n 2 is not O(n) n 2 cn n c The above inequality cannot be satisfied since c must be a constant 34 Analysis of Algorithms

More Big-Oh Examples T(n)=7 n-2 is O(n) need c > 0 and n 0 1 such that 7 n-2 c • n for n n 0 this is true for c = 7 and n 0 = 1 T(n)= 3 n 3 + 20 n 2 + 5 is O(n 3) need c > 0 and n 0 1 such that 3 n 3 + 20 n 2 + 5 c • n 3 for n n 0 this is true for c = 4 and n 0 = 21 T(n)=3 log n + log log n is O(log n) need c > 0 and n 0 1 such that 3 log n + log n c • log n for n n 0 this is true for c = 4 and n 0 = 2 35 Analysis of Algorithms