Definition and finding the limit When substitution results

Definition and finding the limit When substitution results in a 0/0 fraction, the result is called an indeterminate form. The limit of an indeterminate form exists, but to find it you must use a technique, such as factor and cancel.

Calculus Date: 9/26/14 Objective: SWBAT define, calculate & apply properties of limits graphically, numerically and now analytically. Do Now – Mini Quiz 5 minutes Take out a piece of paper. Can be a half sheet. HW Requests: HW: pg 30 SM all In class: worksheets ( possibilities Worksheet limits or Mc. Cafrey) To get ahead, You have to do extra! HW: Complete Worksheets Announcements: Mandatory session Sine and Cosine functions starting with the Unit Circle Quiz Friday

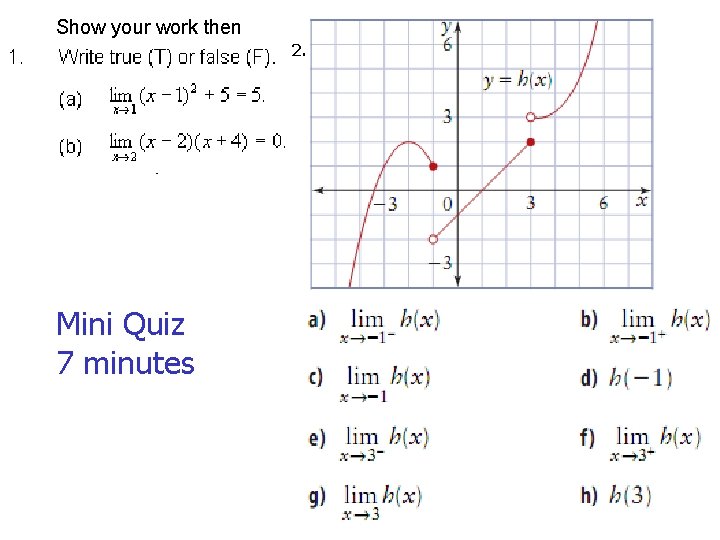
Show your work then 2. Mini Quiz 7 minutes

Techniques-Finding limits for Rational Expressions 1. Try Substitution, if doesn’t work 2. Try Factor and cancel and then 3. Try Substitution again, if doesn’t work 4. Do DNE or +/- infinity check - If the right and left side limit are not equal the limit does not exist - DNE Let’s go to the SM pg #28 #1 -8 (10) HW: pg 30 SM all

Rationalizing Technique If there is a radical in the numerator or the denominator, rationalize, simplify and cancel, then try substitution. Substituting we get Hint: Often you cancel a common term in the numerator and denominator when simplifying

Rationalizing Technique Rationalize, simplify (cancel) and try substitution. Substituting we get = 1 4

Try This Find: 2 f(0)is undefined; 2 is the limit

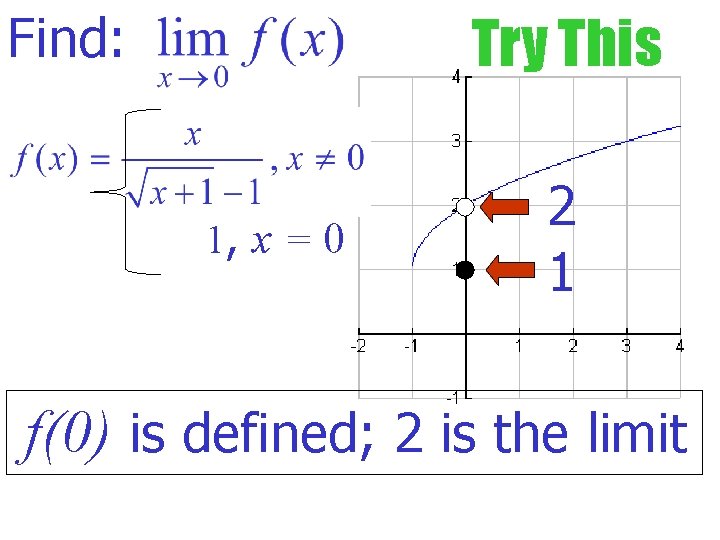
Find: Try This 1, x = 0 2 1 f(0) is defined; 2 is the limit

Try This Find the limit if it exists: DNE

Try This Find: if

Try This Find the limit of f(x) as x approaches 3 where f is defined by:

Example Find the limit if it exists: Try substitution

Example Find the limit if it exists: Substitution doesn’t work…does this mean the limit doesn’t exist?

Use the factor & cancellation technique and are the same except at x=-1

Use the factor & cancellation technique After factoring and cancelling, now try substituting -1 again. =3

Try This s a ? y w Find the limitasif it exists: s u l e u t c l ? a t a l h c t u c k i t ’ f n f i i n h d s t I u be o y o t d g 5 i D in o g

Try This Solve using limit properties and substitution: 6

Try This Find the limit if it exists:

Example Sometimes limits do not exist. Consider: If substitution gives a constant divided by 0, the limit does not exist (DNE)

Try This Find the limit if it exists: Confirm by graphing The limit doesn’t exist

Lesson Close Name 3 ways a limit may fail to exist.

Exit Ticket • In Class: SM – pg 28 #1 -5 • HW: SM pg 30 #1 -15

Try This Find the limit if it exists: -5

Limit properties again The existence or non-existence of f(x) as x approaches c has no bearing on the existence of the limit of f(x) as x approaches c. What matters is…what value does f(x) get very, very close to as x gets very, very close to c. This value is the limit.

Limits, again! Ø In order for a limit to exist at c, the left-hand limit must equal the right hand limit. Ø If the left-hand limit equals the right hand limit, then the limit exists and we write: Watch out for piecewise functions

When finding the limit of a function it is important to let x approach a from both the right and left. If the same value of L is approached by the function the limit exist and

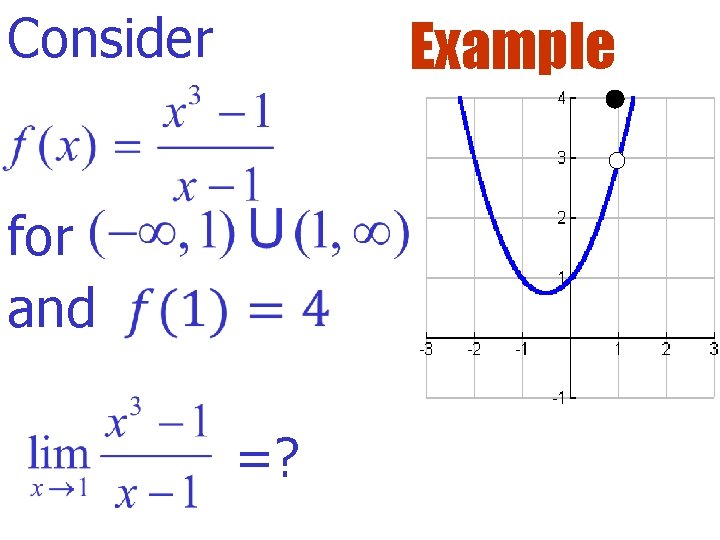
Consider Example for and =?

Try This Graph and find the limit (if it exists): DNE

Example Trig functions may have limits.

Try This

Using the Product Rule Technique

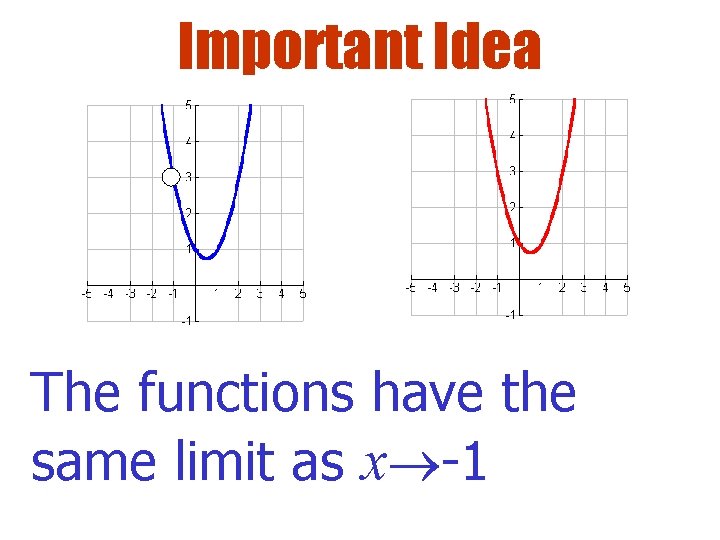
Important Idea The functions have the same limit as x -1

Try This Graph and on the same axes. What is the difference between these graphs?

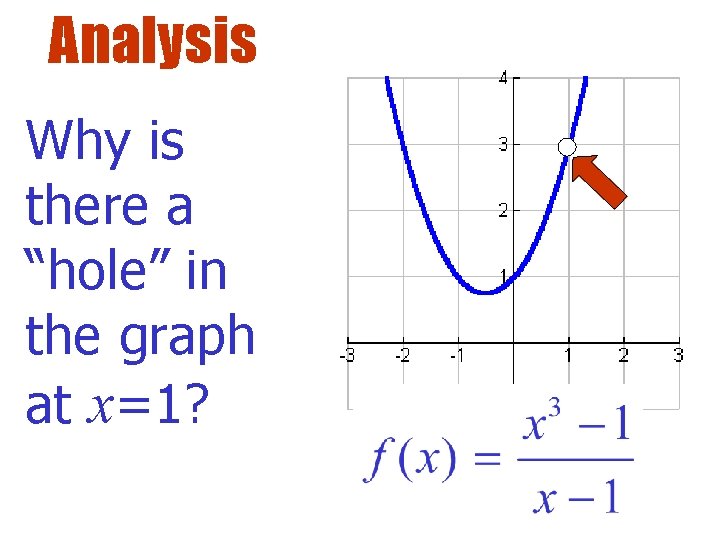
Analysis Why is there a “hole” in the graph at x=1?

Example Consider What happens at x=1? Let x get close to 1 from the left: x. 75. 9. 999 f(x)

Try This Consider Let x get close to 1 from the right: x f(x) 1. 25 1. 1 1. 001

Try This What number does f(x) approach as x approaches 1 from the left and from the right?

Informal Definition of Limit • If f(x) becomes arbitrarily close to a single number L as x approaches a number c from either side, the limit of f(x), as x approaches c, is L.

- Definition of Limit • Let f be a function defined on an open interval containing c (except possibly at c) and let L be a real number. The statement means that for each >0 there exists a >0 such that if then.

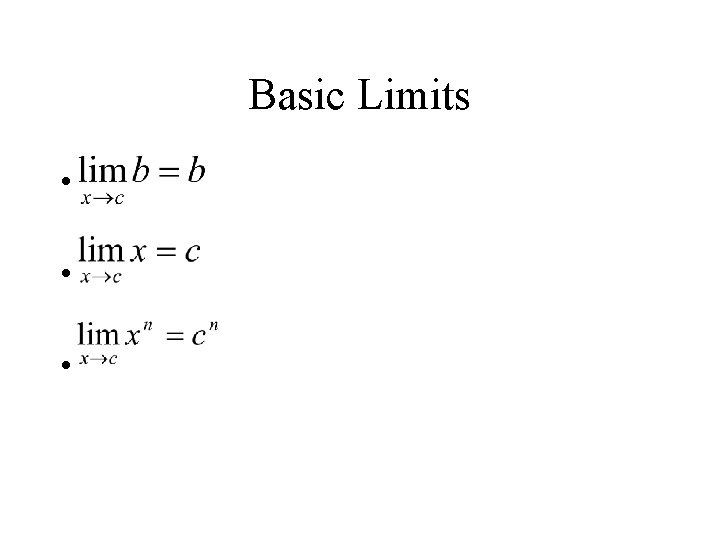
Basic Limits • • •

Constant Function Limits • a and b are both constants • This means that for any constant function f(x) = b, as x approaches any constant a, the limit will always be b.

Linear Function Limits The limit of f(x) = x as x approaches any constant is the constant itself.

Exponential Function Limits Just plug in a for x

Properties �Let and �Scalar multiple: �Sum or difference: �Product: �Quotient: �Power: , if K 0

• Let's try a practice problem. • Property (B) tells us we can split these apart: • Using limit (1) and limit (2) from the basic limits, we get:

Putting it all together • So, This is called the Substitution method

Try This Solve using limit properties and substitution: 25