Definition A linear inequality in two variables x

Definition • A linear inequality in two variables x and y is an inequality that can be written in one of the following forms: Ax + By < C Ax + By > C Ax + By ≤ C Ax + By ≥ C provided A and B are not both zero. • A solution to a linear inequality in two variables is an ordered pair that makes the inequality true.

Graphing a Linear Inequality in Two Variables Step 1 Solve for y, if possible. Step 2 Graph the related equation. Draw a dashed line if the inequality is strict, < or >. Otherwise, draw a solid line. Step 3 Shade above or below the line as follows: • Shade above the line if the inequality is of the form y > mx + b or y ≥ mx + b. • Shade below the line if the inequality is of the form y < mx + b or y ≤ mx + b.

Graphing a Linear Inequality in Two Variables Note: A dashed line indicates that the line is not included in the solution set. A solid line indicates that the line is included in the solution set.

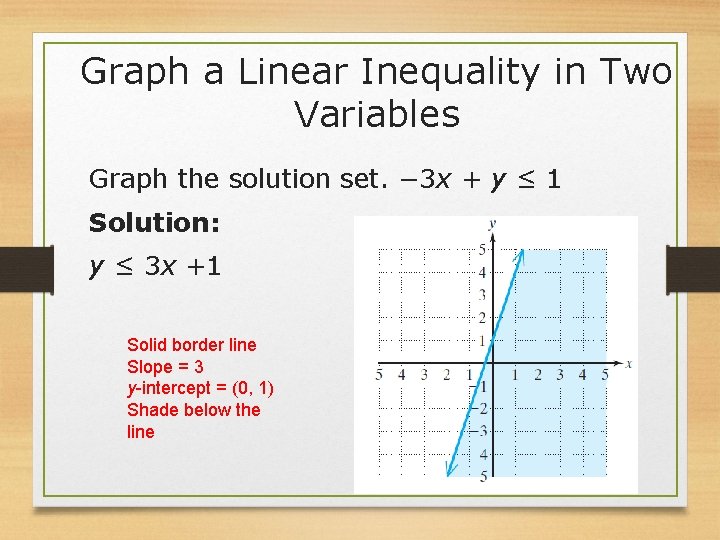
Graph a Linear Inequality in Two Variables Graph the solution set. − 3 x + y ≤ 1 Solution: y ≤ 3 x +1 Solid border line Slope = 3 y-intercept = (0, 1) Shade below the line

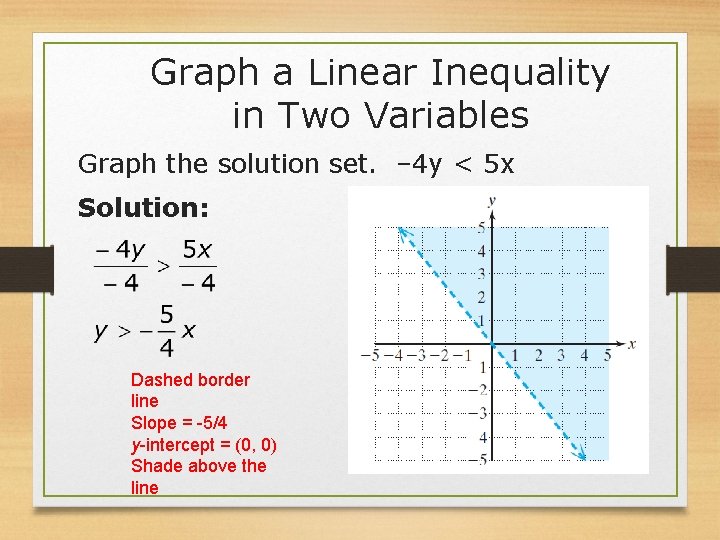
Graph a Linear Inequality in Two Variables Graph the solution set. − 4 y < 5 x Solution: Dashed border line Slope = -5/4 y-intercept = (0, 0) Shade above the line

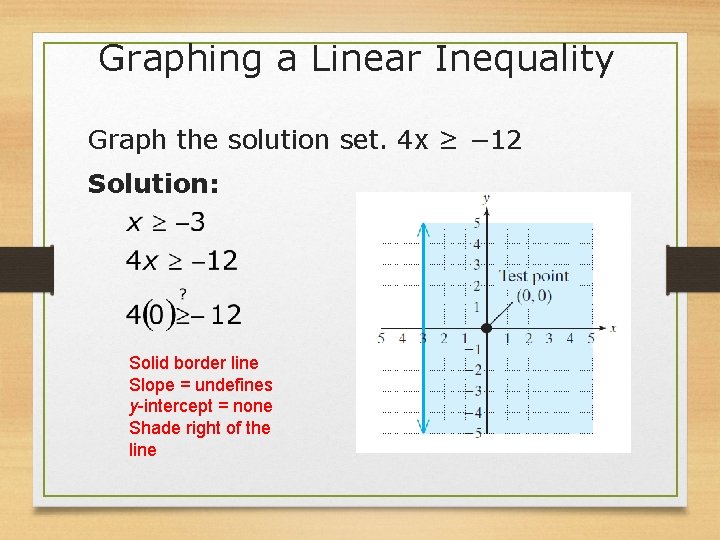
Graphing a Linear Inequality Graph the solution set. 4 x ≥ − 12 Solution: Solid border line Slope = undefines y-intercept = none Shade right of the line

Graphing a System of Linear Inequalities Graph the solution set of the system of inequalities. Solution:

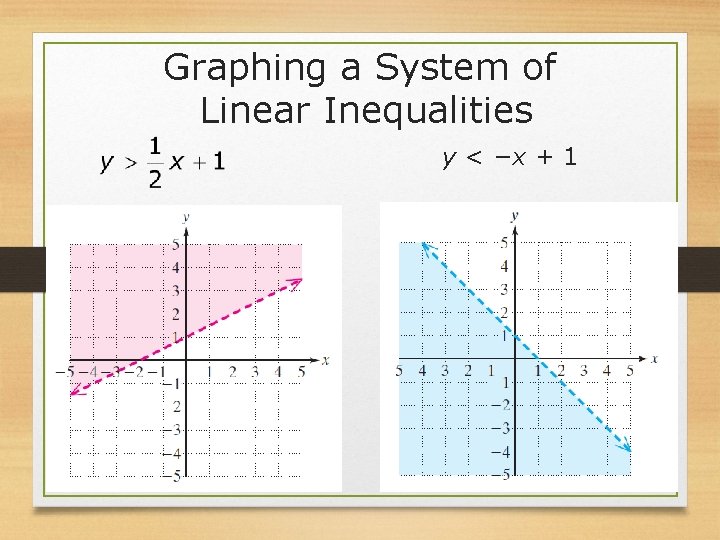
Graphing a System of Linear Inequalities y < −x + 1

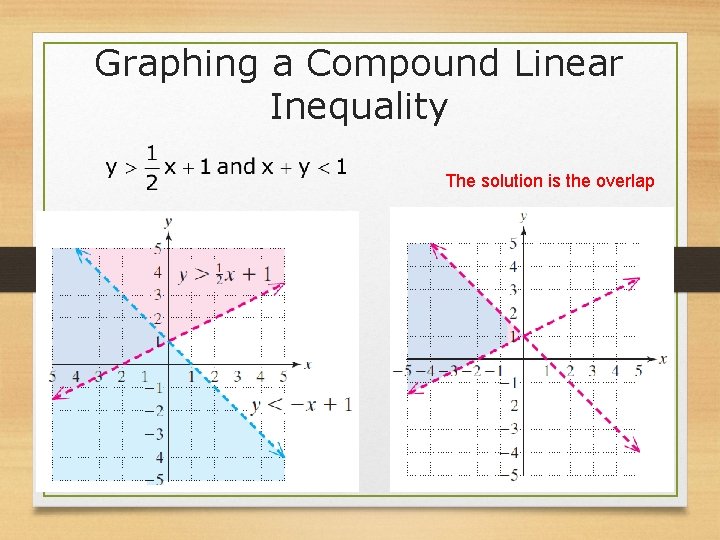
Graphing a Compound Linear Inequality The solution is the overlap

Graphing a System of Linear Inequalities Describe the region of the plane defined by the system of inequalities. The intersection of these regions is the set of points in the second quadrant (with the boundaries included).