Definite Integrals in Physics Background and Examples Integral

Definite Integrals in Physics Background and Examples

Integral as anti-derivative • Let f(x) be a continuous function. The derivative of the function f’(x) = df/dx is itself a function that describes the slope of the tangent line to f(x) • The integral of a function is the anti-derivative of the function and it describes the area under the graph of f(x)

Examples in kinematics

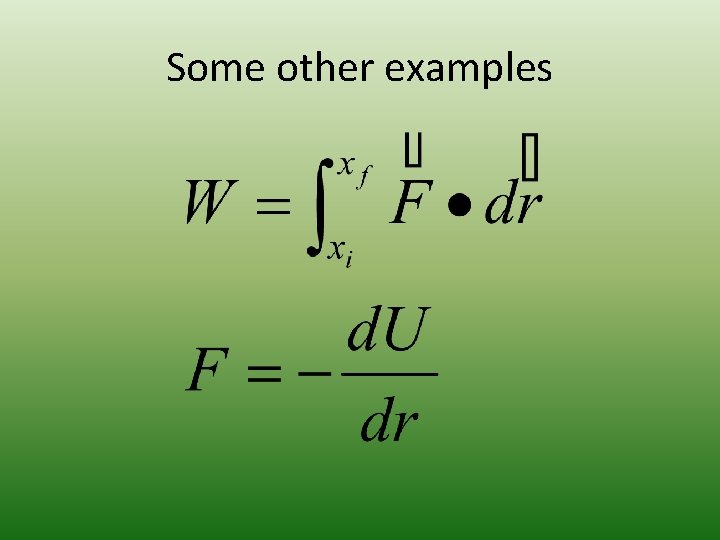
Some other examples

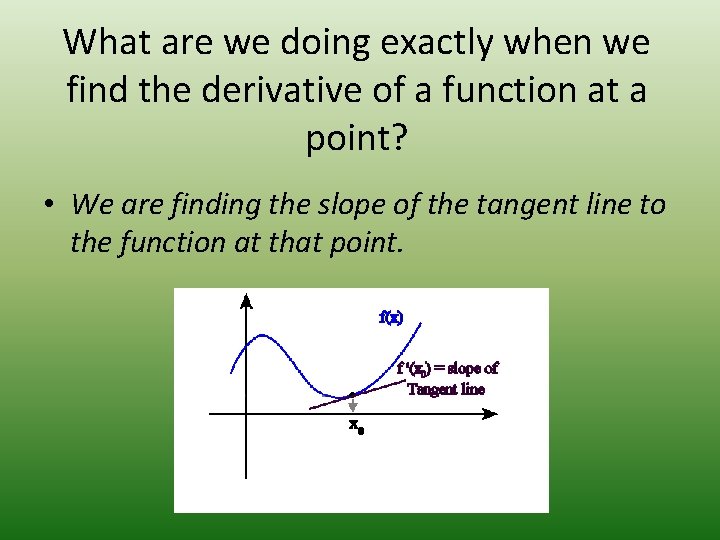
What are we doing exactly when we find the derivative of a function at a point? • We are finding the slope of the tangent line to the function at that point.

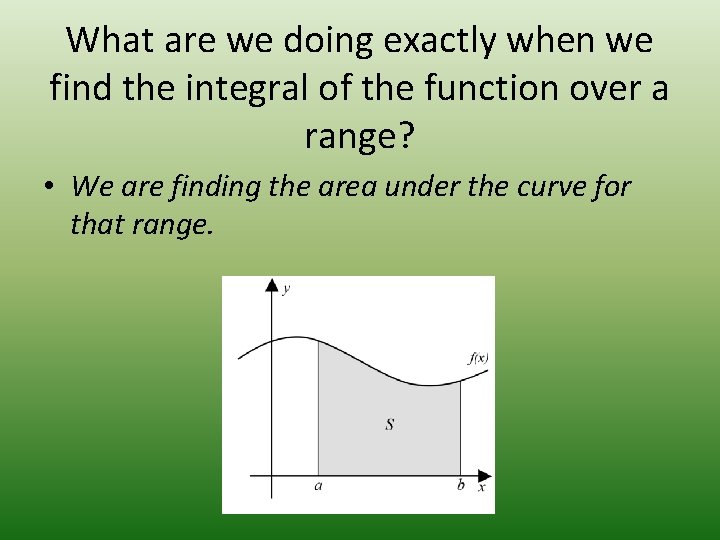
What are we doing exactly when we find the integral of the function over a range? • We are finding the area under the curve for that range.

“New” application of integration for us • Just like adding up the areas of an infinite number of rectangles under the curve to determine the total area, we want to break up continuous objects into an infinite number of tiny pieces and then add them up • (Slightly) older application: When force varies with position F(r), then we must take an infinite number of tiny steps, calculating the work it takes for each little step, and adding them to get the total work done

Important Rule

Try some samples

Finding mass of a continuous object of length L with variable density Linear density (kg/m) can be represented by L x

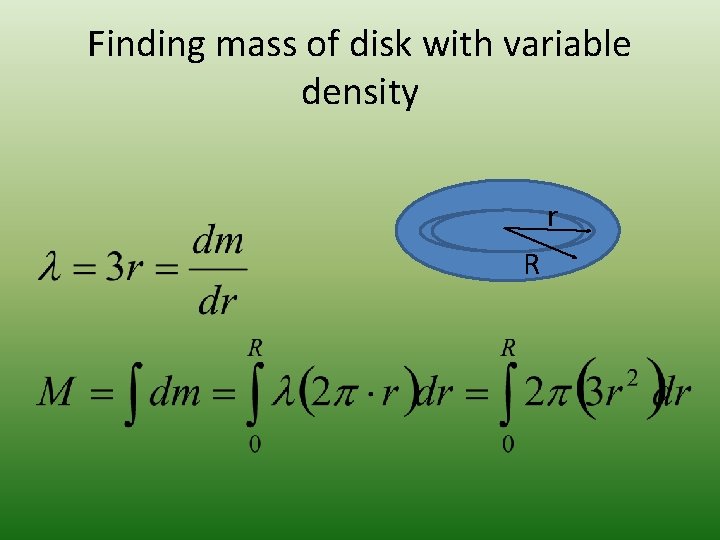
Finding mass of disk with variable density r R

Finding CM of continuous object with variable density • First calculate the total mass as shown in previous slide • Apply the CM formula for continuous objects