DEFINISI Peluang bersyarat A bila B diketahui dilambangkan

DEFINISI • Peluang bersyarat A bila B diketahui dilambangkan dengan P(A|B) dan didefinisikan sebagai jika P(B) > 0

PELUANG BERSYARAT • Misal satu dadu dilantunkan didifinisikan A kejadian angka lebih besar dari 3 dan B angka kuadrat • A=(4, 5, 6) dan B= (1, 4) • P(B)=2/6. berapa peluang B jika diketahui yang muncuk diantara 4, 5, 6 atau dengan syarat A • Jika sebagai syarat berarti A sebagai ruang contoh dari B dan anggota dari B yang tidak sesuai dengan A tidak diperhitungkan--- A. B sehingga peluang P(B/A)=1/3 • Jika dengan rumus P(B/A)=1/6 / 3/6=1/3

• • Jika muncul anka genap dua kali ganjil P(B/A)=2/5 Jika pakai rumus P(B/A)=2/9 / 5/9 = 2/5

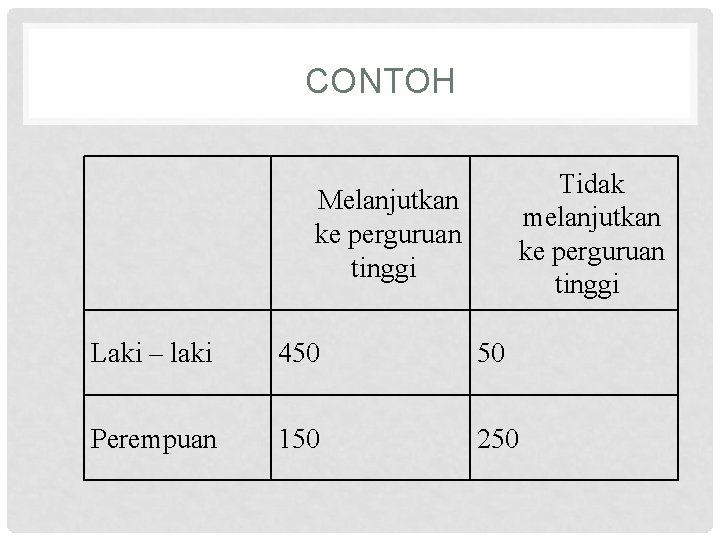
CONTOH Tidak melanjutkan ke perguruan tinggi Melanjutkan ke perguruan tinggi Laki – laki 450 50 Perempuan 150 250

Perhatikan kejadian – kejadian berikut : L : kejadian yang terpilih laki - laki K: kejadian yang terpilih adalah orang yang melanjutkan ke perguruan tinggi Dengan menggunakan ruang contoh yang dipersempit K, maka akan didapatkan P(L|K) = 450/600 = ¾

• Misalkan n(A) melambangkan banyaknya unsur dalam himpunan A

• Contoh • Kotak berisi 20 sekering dan lima diantaranya cacat. Jika diambil dua sekering satu demi satu tanpa pengembalian, berapa peluang dua sekering cacat. • Jawab • Misal A= sekering pertama cacat • Misal B= sekering kedua cacat • P(A. B)=P(A)P(B/A) • P(A. B)=(5/20)(4/19)=1/19 • Secara umum • P(A. B. C. D)=P(A)P(A/B)P(C/A. B)P(D/A. B. C)

KEJADIAN BEBAS • Jika pengambilan sekering dengan pengembalian, maka • P(A. B)=P(A)P(B/A) • P(A. B)=(5/20)=25/400 • Ini berarti P(B/A)=P(B) • Kejadian bebas • P(A. B)=P(A)P(B)

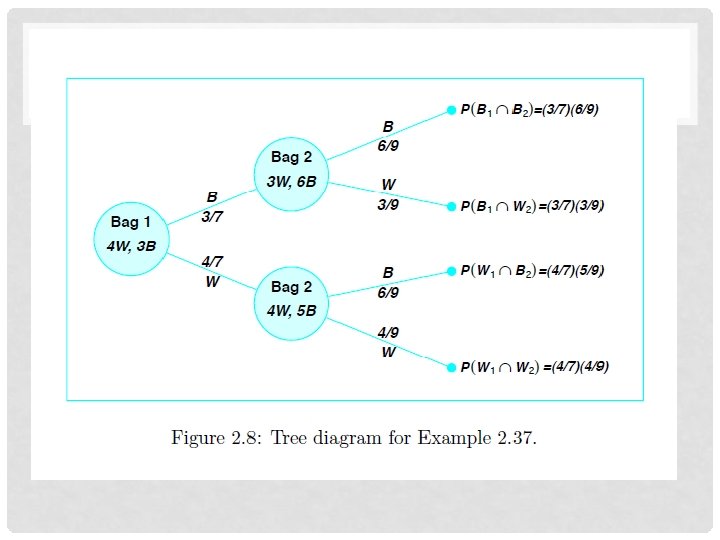
• Suatu kantung berisi 4 bola putih dan 3 bola hitam. Kantung kedua berisi 3 bola putih dan 5 bola hitam. Satu bola diambil dari kantung pertama tanpa melihatnya dan dimasukkan ke kantung kedua. Berapa peluang mengambil bola hitam dari kantung kedua.

• Contoh • Dua dadu dilantunkan dua kali. Berapa peluang mendapat jumlah 7 dan 11 dalam dua kali lantunan. • Jawab • Misal A 1, A 2 kejadian bebas muncul angka 7 lantunan 1 dan 2, B 1, B 2 muncul angka 11 lantunan 1 dan 2 • P((A 1. B 2)U(B 1. A 2))= P((A 1. B 2)+(B 1. A 2)) • = P(A 1)P(B 2)+P(B 1)P(A 2) • =(1/16)(1/18)+(1/18)(1/16)=1/54

• Suatu sistem penyediaan air terdiri atas satu sumber, lima pompa air, dan satu tujuan. Bila tiap rumah pompa dapat dijalankan pada waktu to dengan peluang p, bila antar pompa bebas. Carilah peluang R(p) bahwa air mengalir ke tujuan. (R(p)=keterandalan sistem) • |-- --1 -------2 ------| • ->--|--- ---5< |--- tujuan • |-- --3 -------4 ------|

• Misal Ai=pompa i dapat dijalankan pada waktu to. P(A 1)=. . . =P(A 5)=p. Misal B= air mengalir ke tujuan pada waktu to. P(B)=R(p) • P(B)= P(B. A 5)+P(B. A 5*) • =P(B/A 5)P(A 5)+P(B/A 5*)P(A 5*) • =p. P(B/A 5)+(1 -p)P(B/A 5*) • P(B/A 5*)=P((A 1. A 2)U(A 3. A 4)/A 5*) • =P(A 1. A 2/A 5*)+P(A 3. A 4/A 5*)-P(A 1 A 2 A 3 A 4/A 5*) • = p 2+p 2 -p 4=2 p 2 +p 4 • P(B/A 5)=P(A 2 UA 4/A 5) • =P(A 2/A 5)+P(A 4/A 5)-P(A 2 A 4/A 5) • = p +p – p 2= 2 p – p 2 • Sehingga P(B)= p(2 p-p 2)+(1 -p)(2 p 2 – p 4) = 4 p 2 – 3 p 3 – p 4 + p 5

CONTOH LAIN Peluang Kereta Api Gajayana berangkat tepat pada waktunya adalah P(B) = 0. 85, peluang Kereta Api Gajayana datang tepat pada waktunya adalah P(D) = 0. 90 dan peluang kereta api tersebut berangkat dan datang tepat pada waktunya adalah P(B D) = 0. 75. Hitung peluang bahwa Kereta Api Gajayana itu (a) datang tepat pada waktunya bila diketahui kereta api tersebut berangkat tepat pada waktunya, dan (B) berangkat tepat pada waktunya bila diketahui kereta api tersebut datang tepat pada waktunya.

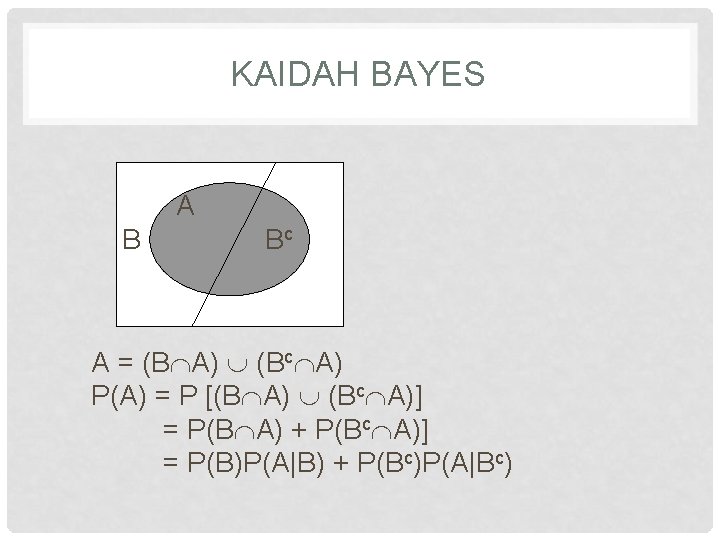
KAIDAH BAYES A B Bc A = (B A) (Bc A) P(A) = P [(B A) (Bc A)] = P(B A) + P(Bc A)] = P(B)P(A|B) + P(Bc)P(A|Bc)

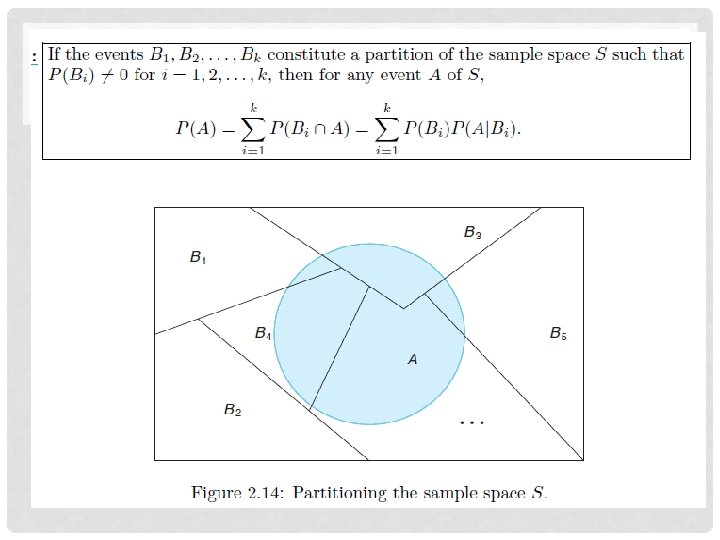
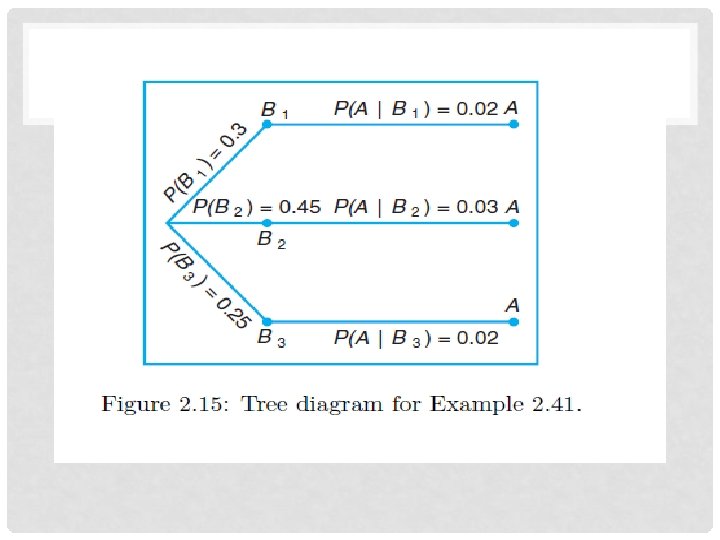
KAIDAH TOTAL PELUANG Bila kejadian – kejadian Bi untuk i = 1, 2, …, k, maka untuk sembarang kejadian A yang merupakan himpunan bagian S berlaku P(A) = P(B 1) P(A|B 1) + P(B 2) P(A|B 2) + … + P(Bk) P(A|Bk).

CONTOH 1 Tiga wakil partai A, B dan C mencalonkan diri sebagai presiden. Peluang wakil dari partai A terpilih sebagai presiden adalah 0. 4, peluang wakil dari partai B terpilih adalah 0. 3 dan peluang wakil dari partai C terpilih adalah 0. 3. Seandainya wakil dari partai A terpilih sebagai presiden, peluang terjadinya kenaikan harga BBM adalah 0. 7. Seandainya yang terpilih adalah wakil dari partai B, peluang terjadinya kenaikan harga BBM adalah 0. 4. Bila yang terpilih adalah wakil dari partai C maka peluang terjadinya kenaikan harga BBM adalah 0. 6. Berapa peluang terjadinya kenaikan harga BBM ?

CONTOH 2 • Sebuah toko menjual bola lampu. Empat puluh lima persen dari bola lampu yang dijual toko tersebut diproduksi oleh pabrik A dan sisanya diproduksi oleh pabrik B. Bola lampu yang diproduksi pabrik A mempunyai peluang cacat sebesar 3 persen sedangkan yang diproduksi pabrik B mempunyai peluang cacat sebesar 5 persen. Bila seseorang membeli bola lampu dari toko tersebut, berapa peluang dia akan mendapatkan bola lampu yang cacat?

KAIDAH BAYES Jika kejadian – kejadian B 1, B 2, …, Bk merupakan sekatan dari ruang contoh S dengan P(Bi) 0 untuk I = 1, 2, …, k, maka untuk sembarang kejadian A yang bersifat P(A) 0,

• Untuk masalah dalam Contoh 1 misalkan ada orang yang tidak mengetahui siapa yang menjadi presiden karena dia tinggal di pelosok daerah. Bila beberapa waktu kemudian ternyata harga BBM naik, berapa peluang bahwa yang menjadi presiden adalah wakil dari partai A?

Untuk masalah pada contoh 2, misalkan ada seseorang yang membeli bola lampu dari toko tersebut. Setelah sampai rumah dan dicoba, ternyata lampu tersebut cacat. Berapa peluang bahwa lampu tersebut diproduksi oleh pabrik A?

SOAL - SOAL 1. Proses produksi bola lampu dalam suatu pabrik dibagi dalam empat shift. Pada suatu hari, 1% dari bola lampu yang diproduksi oleh shift pertama rusak, 3% dari yang diproduksi shift kedua rusak, 2% dari yang diproduksi shift ketiga rusak dan 1% dari yang diproduksi oleh shift keempat rusak. Bila produktivitas keempat shift tersebut sama, berapa peluang bola lampu yang diproduksi pada hari itu rusak?

2. Kantong A berisi 3 bola biru, 2 bola merah dan 5 bola hijau. Kantong B berisi 1 bola biru, 4 merah dan 3 hijau. Sebuah bola diambil dari kantong A dan tanpa dilihat warnanya kemudian dimasukkan ke kantong B. Lalu dari kantong B diambil 1 bola. Berapa peluang terambilnya bola hijau.

3. Suatu produk yang dijual oleh toko A, 30% - nya diproduksi oleh pabrik X dan sisanya diproduksi oleh pabrik Y. Produk yang diproduksi oleh pabrik X mempunyai peluang cacat sebesar 0. 05 dan produk yang diproduksi pabrik Y mempunyai peluang cacat sebesar 0. 07. Bila Dion membeli produk tersebut dari toko A dan ternyata produk tersebut cacat, berapa peluang bahwa produk tersebut adalah produk yang diproduksi oleh pabrik X?

4. Suatu kuliah Pengantar Teori Peluang diikuti oleh 50 mahasiswa tahun ke-2, 15 mahasiswa tahun ke-3 dan 10 mahasiswa tahun ke-4. Diketahui mahasiswa yang mendapat nilai A adalah 10 orang dari mahasiswa tahun ke-2, 8 orang dari mahasiswa tahun ke-3 dan 5 orang dari mahasiswa tahun ke-4. Bila seorang mahasiswa dipilih secara acak, berapa peluang dia : • Mendapat nilai A, bila diketahui dia mahasiswa dari tahun ke-3? • Mendapat nilai A? • Mahasiswa tahun ke-2, bila diketahui dia mendapat nilai A?

LATIHAN • Suatu kotak berisi 4 bola putih 3 bola hitam sedang kantung kedua 3 bola putih dan 5 bola hitam. Suatu bola diambil dari kantung pertama tanpa melihatnya dimasukkan kantung ke 2. Berapakah peluang mengambil bola hitam dari kantung kedua. • Sebuah kotak berisi 5 bola hitam dan 3 hijau. Tiga bola diambil secara berurutan dengan pengembalian. Berapa peluang ketiga bola berwarna sama dan berapa peluang kedua warna terambil. • Seorang pengusaha real estate mempunyai delapan kunci indukuntuk membuka beberapa rumah baru. Suatu rumah hanya dapat dibuka dengan kunci tertentu. Bila 40 % dari rumah biasanya tak terkunci, berapakah peluang pengusaha tersebut dapat masuk ke dalam rumah tertentu bila dia hanya membawa 3 kunci secara acak.