Defending and attacking a network of two arcs

Defending and attacking a network of two arcs subject to traffic congestion 2013 Reliability Engineering and System Safety Presenter : Yen Fen Kao Advisor : Yeong Sung Lin

2 Agenda Introduction The model Results Conclusions

3 Introduction A growing literature analyzes how networks and infrastructures are defended and attacked. A largely separate literature analyzes traffic congestion, assuming neither defense nor attack. This paper is to our knowledge the first to develop an understanding of how the two literatures can be merged.

4 Introduction we consider a simple model in which multiple drivers choose the more time-efficient of two arcs of different lengths. Both arcs are subjected to traffic congestion, and also to interdiction. We describe the interdiction as being performed by a terrorist, but it may also be performed by a government organization, for example for interdiction of drug smuggling [45]. In our model, the government allocates a resource to protect travel along the two arcs. The terrorist has the opposite objective of interdicting the arcs.

5 Introduction There are three possible outcomes: both arcs operate; one arc operates while the other is blocked; or both arcs are blocked. The drivers have reservation travel times such that if an individual driver’s reservation travel time is exceeded, the driver prefers not to travel. The objective function, which the government minimizes and the terrorist maximizes, weights the travel times by the number of drivers along the two arcs, and weights the average penalty (which equals the trip value) suffered by those preferring not to travel by the number of drivers who do not travel. Since the travel times in the objective function are computed taking congestion into account, this objective function implicitly considers travel time delays, but also an estimate of the losses to those who choose not to travel due to congestion.

6 Introduction Azaiez and Bier [2] consider the optimal resource allocation for security in reliability systems. Dighe et al. [15] consider secrecy in defensive allocations as a strategy for achieving more cost-effective attacker deterrence. Zhuang and Bier [47] consider defender resource allocation for countering both terrorism and natural disasters.

7 Introduction Brown et al. [10] consider defender–attacker–defender models. First, the defender invests in protecting its infrastructure, subject to a budget constraint; then a resource-constrained attack is carried out; and finally, the defender operates the residual system as well as possible. Brown et al. [10] illustrate their approach with applications to border control, the US strategic petroleum reserve, and electric power grids. Ukkusuri and Yushimito [41] present a methodology to assess the criticality of highway-transportation networks. They use concepts from the science of complicated networks to assess the importance of highway networks, using travel time as a performance measure to assess criticality.

8 Introduction Nagurney and Qiang [25, 26] present an efficiency measure for congested networks, accounting for demands and costs and the underlying behavior of network users. However, most such models do not address problems of transportation security. To our knowledge there have not yet been any models of transportation infrastructure that take into account the effects of congestion in systems with a strategic attacker, a strategic defender, and strategic drivers.

9 Introduction The model suggested in this paper relies on a contest-success function commonly used in models of economic conflict when players have opposite preferences [36, 40]. Contest-success functions have been less commonly used in the war and combat literature, where Lanchester [19] differential equations have been more common, but are equally applicable to war and combat. In addition, we explicitly include a model of congestion, based on the approach taken in Small and Verhoef [37].

10 Agenda Introduction The model Results Conclusions

11 The model - Notation

12 The model - Notation

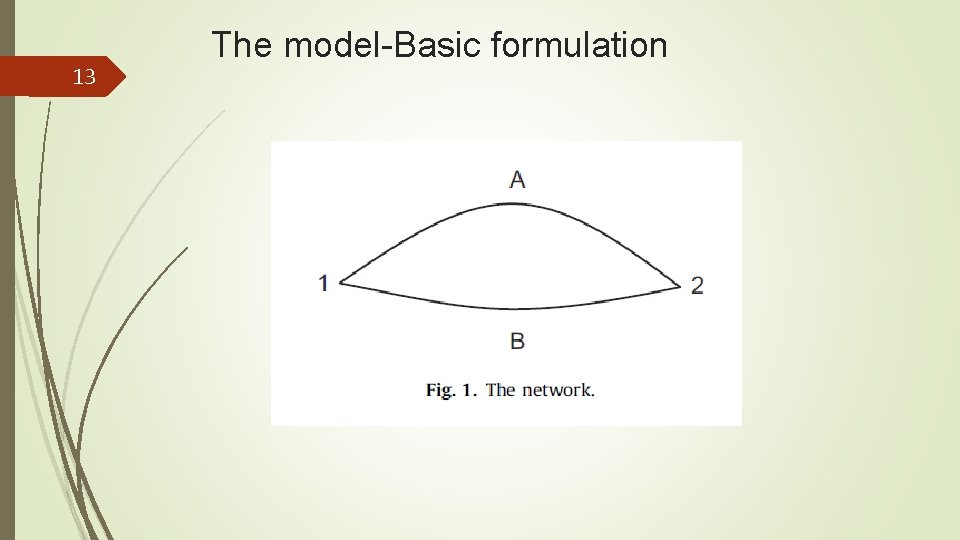
13 The model-Basic formulation

14 The model-Basic formulation It is common and realistic to assume that the government chooses its protection effort first and the terrorist chooses its interdiction effort second. However, since we consider a zero-sum game, the same equilibrium solution is obtained regardless of whether the government and the terrorist choose their strategies simultaneously and independently, or one player chooses first and the other player responds. This follows from Von Neumann’s [42] min–max theorem, and from Von Neumann and Morgenstern’s [43] finding (Section 15. 3. 1) that zero-sum two-person games are solvable by backward induction. (For non-zero-sum games, simultaneous and sequential games yield different solutions. )

15 The model-Basic formulation After the government and the terrorist have made their decisions, the drivers choose the optimal arc, A or B. Both the structure of the network and all parameter values are common knowledge. The distance (in miles) along arc k is. The average speed (in miles/h) along arc k is. The average time to travel from node 1 to node 2 along arc k is given by (in h), where

16 The model-Basic formulation We define the traffic density, (in drivers/h), as the average number of drivers arriving at the destination point (or, equivalently, passing any given point) along arc k per unit time. The average number of drivers on arc k at any point in time is thus

17 The model-Basic formulation Example 1. Consider a benchmark system with no congestion. Set miles, drivers/h, and miles/h. Eqs. (1) and (2) give and drivers. Set miles. Making drivers indifferent between the two arcs means ; Eq. (1) then gives the speed to be miles/h. If neither nor is specified, Eq. (2) is indeterminate for arc B, which means that there can be either many or few drivers on arc B. This illustrates how congestion plays no role in this example.

18 The model-Basic formulation We model congestion along arc k by Where congestion. is a parameter that expresses the effect of Eq. (3) states that the traffic density reaches its maximum when speed is at its optimum level, .

19 The model-Basic formulation Using data from a four-lane section of the Washington (DC) Beltway, Boardman and Lave [8] have quantified the parameters in Eq. (3) as follows Where is in drivers/h per lane.

20 The model-Basic formulation Example 2. Assume that drivers arrive at node 1 per hour, and seek to proceed as quickly as possible to node 2. The drivers distribute themselves across arcs A and B so that ; i. e Although drivers may be boundedly rational and have incomplete information, we consider as a reasonable assumption that drivers distribute themselves to achieve. Applying Eq. (1) gives Which Hence, more drivers travel along the shorter arc, B, but at a lower speed than the drivers traveling along arc A.

21 The model-Basic formulation The government exerts effort at unit cost to protect travel along arc k. The terrorist exerts effort at unit cost to interdict travel along arc k. The government has a total defensive budget r, and must satisfy The terrorist has a resource R, obtained through sponsorship or in other ways, allocated such that

22 The model-Basic formulation We define the travel reliability along arc k as the probability that arc k will be passable. We model using the common ratio form contest-success function [36, 40], which expresses the probability that there will not be a successful attack on arc k where is a parameter expressing the intensity of the contest, yielding and.

23 The model-Basic formulation If both arcs are operational, drivers distribute themselves across both arcs so that they experience the same travel time on both arcs. If an attack on one arc succeeds, then the other arc is succeed, then no arcs are passable, and all drivers must stay home. Assume that D drivers want to travel through the network. If D exceeds the network capacity, then the excess drivers cannot travel, and stay at home. We define a driver’s reservation travel time as the largest acceptable time for travel from node 1 to node 2. It can be determined either empirically or by survey methods such as contingent valuation. We interpret this as the driver’s value of traveling (i. e. , the trip value).

24 The model-Basic formulation If the actual travel time exceeds the reservation travel time, the driver prefers not to travel, and stays at home. If the actual travel time is less than the reservation travel time, the driver enjoys both the trip value and the savings in travel time. We assume that the D drivers have reservation travel times uniformly distributed between and , where , as shown in Fig. 2. Assume that the actual travel time is t. Then drivers with small reservation travel times (between and ) prefer not to travel, and drivers with large reservation travel times (between and ) prefer to travel.

25 The model - Special formulation when one arc is blocked Assume that arc k is not blocked, while arc j is blocked, . We search for equilibrium on arc k where the marginal driver with travel time is indifferent between traveling and not traveling. This means that has the joint interpretation of this marginal driver’s travel time on arc k, and the driver being indifferent between traveling and not traveling. In this equilibrium, it is straightforward that there will be drivers on arc k, and drivers who prefer not to travel. Inserting into Eq. (3) and applying Eq. (1) gives

26 The model - Special formulation when one arc is blocked Eq. (10) determines the travel time when a non-zero number of drivers prefers not to travel. In that case, the travel time on arc k must also equal the reservation travel time of a driver who is indifferent between traveling and not traveling. Identifying that value simultaneously specifies the number of drivers on the left-hand side of Eq. (10). All drivers on arc k have travel time , which means that they travel at speed Sk. Hence, the drivers with reservation travel times between and , on the left-hand side of Eq. (10), enjoy a time savings relative to their reservation travel time. On the other hand, the remaining drivers prefer not to travel, since their reservation travel times are lower than.

27 The model - Special formulation when one arc is blocked The real solution is given by which specifies the travel time on arc k when the other arc is blocked.

28 The model - Special formulation when one arc is blocked Example 3. Extending Example 2, assume that the value of and when both arcs are operational is equal to the lower bound of. Hence, under these conditions, all drivers would prefer to travel, since by definition none have reservation travel times below. Now assume that arc A is blocked. Arc B can maximally carry 2490 drivers if miles/h, which means a travel time of. Assume. Inserting these numerical values into Eq. (11) gives , drivers, where the subscript ‘‘sn’’ denotes that there was a successful attack on arc A but no successful attack on arc B.

29 The model - Special formulation when one arc is blocked Our result shows that the drivers speed up above the speed of 35. 34 miles/h that maximizes the carrying capacity of arc B, in order to shorten their travel time below 2. 12 h, thus causing congestion and allowing only 2487 drivers to travel (which means that three of the 2490 drivers must stay home). In return, these 2487 drivers enjoy a driving time of , which is less than the 2. 12 h without congestion, but more than the 1. 58 h when both arcs operate. Analogously, when arc B is blocked, we get , and drivers, where the subscript ‘‘ns’’ denotes no successful attack on arc A and a successful attack on arc B. Thus, arc A can carry fewer drivers than arc B, but at a higher speed, resulting in a marginally longer travel time due to the greater length of arc A.

30 The model - General formulation and solution Inserting from Eq. (1) into Eq. (3) shows that as the travel time becomes sufficiently small, congestion can force the density to zero. The government seeks to balance the competing objectives of low travel time, high density, and few drivers unable to travel. We thus formulate an objective function weighting the travel time by the number of drivers experiencing this travel time, and weighting the penalty for not traveling (also denominated in hours, and represented by the reservation travel time) by the number of drivers who do not travel due to congestion.

31 The model - General formulation and solution If both arcs are passable, which occurs with probability , the total travel time is proportional to , which weights the travel time along each arc by the density along that arc, where the subscript ‘‘nn’’ means that there was no successful attack on either arc. Moreover, since , the expression expresses the loss for those who travel. In addition, the drivers who do not travel have average trip values of , because their reservation travel times are uniformly distributed; see Fig. 2. Hence, losses for those who do not travel are proportional to. When , all demand is served under normal circumstances. Inserting Eqs. (1) and (3) into gives which specifies the corresponding equilibrium travel time when both arcs are operational.

32 The model - General formulation and solution With probability , there is no successful attack on arc A, but a successful attack on arc B. The quantity , which can be determined using Eq. (3), is the density on arc A when arc B is blocked, where the subscript ‘‘ns’’ means no successful attack on arc A, but a successful attack on arc B. Hence, gives the rate of travel-time losses along arc A for those who travel, and gives the rate of losses for those who do not travel. Analogously, with probability , there is a successful attack on arc A, but no successful attack on arc B. The quantity again gives the density on the operational arc B when arc A is blocked, where the subscript ‘‘sn’’ means a successful attack on arc A and no successful attack on arc B. Hence, gives the rate of travel-time losses along arc B for those who travel, and expresses the rate of lost trip values for those who do not travel.

33 The model - General formulation and solution Finally, with probability , there are successful attacks on both arcs. This gives zero density on both arcs. Hence, expresses the rate of lost trip values for travelers being unable to travel in this condition. We thus get the objective function which the government minimizes and the terrorist maximizes. In (13), the government’s strategic decision variable is , the terrorist’s strategic decision variable is , and each driver’s two strategic choices are whether to travel at all, and if so, whether to travel on arc A or arc B (with the restriction that a blocked arc cannot be chosen).

34 The model - General formulation and solution The government exerts effort in an attempt to ensure large values of and. Analogously, the terrorist exerts effort to achieve small values of and. Solving Eqs. (7) and (8) with respect to the defense and attack efforts and , respectively, gives and. Inserting these into Eq. (9) and Eq. (9) into Eq. (13) and then applying Eqs. (1) and (3) gives our objective function as a function of the free choice variables and. The expected traffic density , which expresses the expected average number of drivers arriving at the destination point per time unit (accounting for the probabilities of successful arc interdiction), is

35 The model - General formulation and solution This expression weights the traffic density under each condition by the probability of that condition. Hence, DED expresses the expected average number of drivers not traveling per time unit, which we refer to as the density of lost trips. Note that Eq. (14) assigns zero weight to the event that occurs with probability , which reflects the fact that the density of travelers is zero when both arcs are blocked. ED can thus be arbitrarily close to zero when the terrorist is likely to be successful in blocking both arcs. In addition, the conditional expected travel time Et, given that at least one arc is passable, is

36 The model - General formulation and solution The objective function in Eq. (13) can be optimized considering only and , since the values of and follow from Eqs. (7) and (8), respectively. Therefore, we assume that the government chooses to minimize the objective function in Eq. (13), and the terrorist chooses to maximize it. Since the game is zero-sum, Von Neumann’s [42] min–max theorem implies that the same solution follows regardless of whether the government and the terrorist choose their strategies simultaneously and independently, the government moves first to minimize the maximum value of f that the terrorist can obtain by choosing its best response (min–max), or the terrorist moves first to maximize the minimum value of f obtainable by the government playing its best response (max–min). Von Neumann and Morgenstern’s [43] proposal (Section 15. 3. 1) of solving the zero-sum game by backward induction, which is the common method to solve sequential games, gives a more complicated analyzis than solving the simultaneous game. We thus solve the simultaneous game.

37 The model - General formulation and solution Differentiating Eq. (13) gives Eqs. (A 1) and (A 2) in Appendix A, which are solved to yield The quantities S, A, B, and F in Eq. (16) are computed according to Eq. (13), using the values of and given in Eq. (11), and the value of specified in Eq. (12).

38 Agenda Introduction The model Results Conclusions

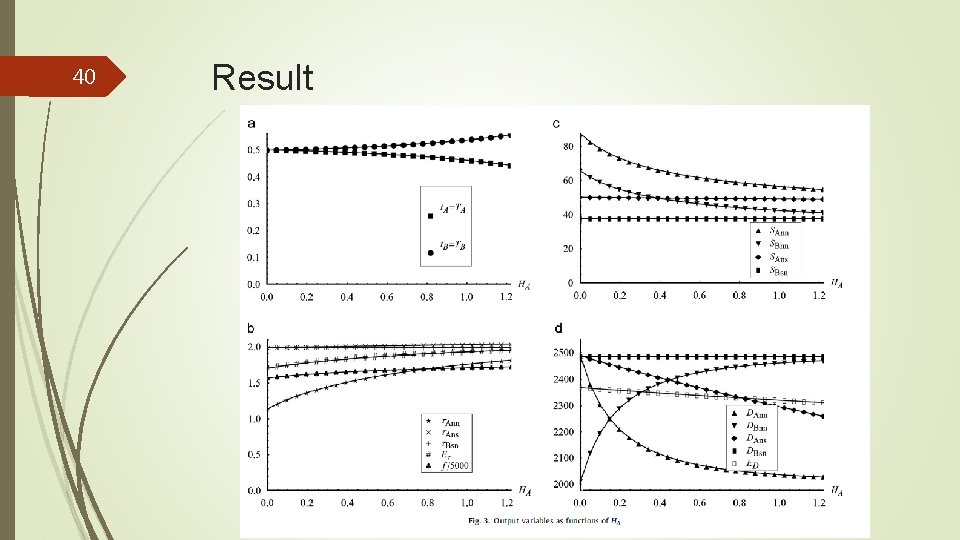
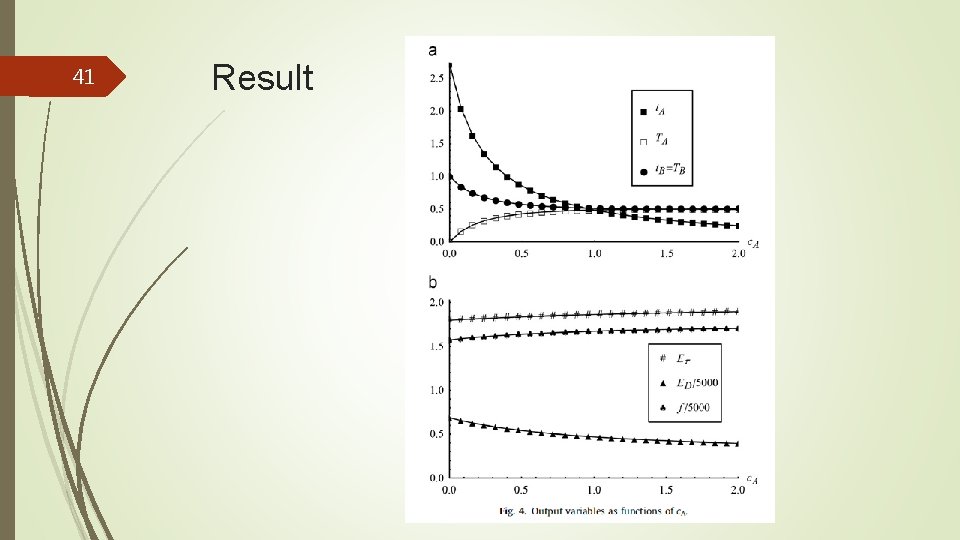
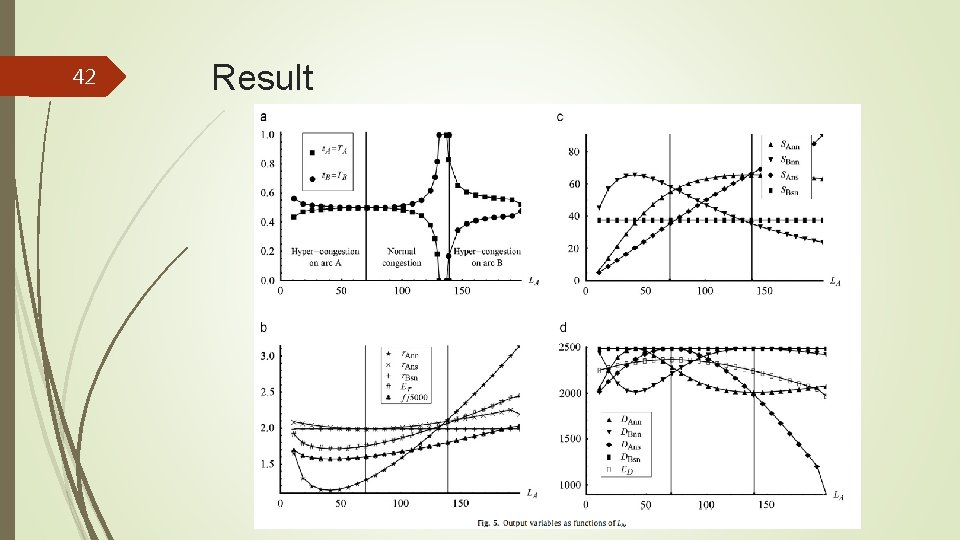
39 Result We use the following baseline parameter values：

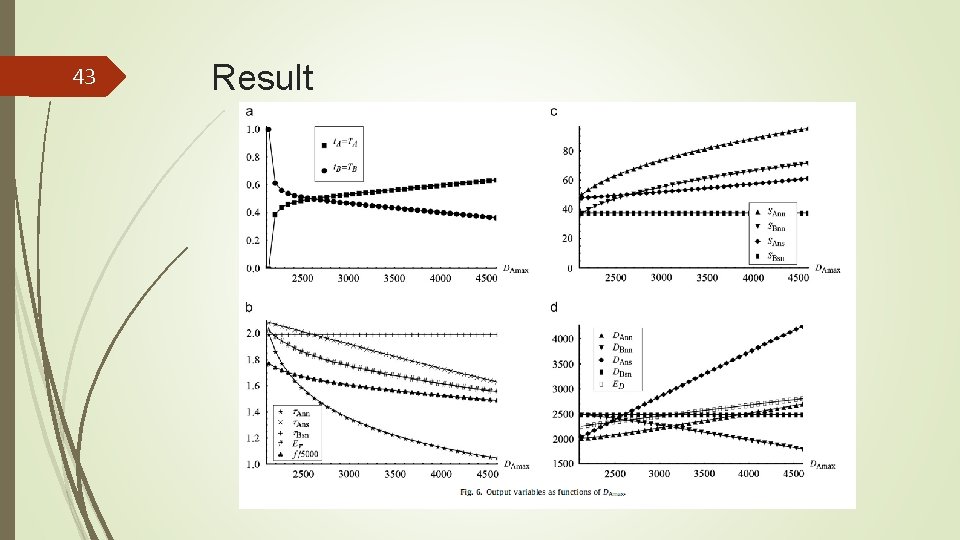
40 Result

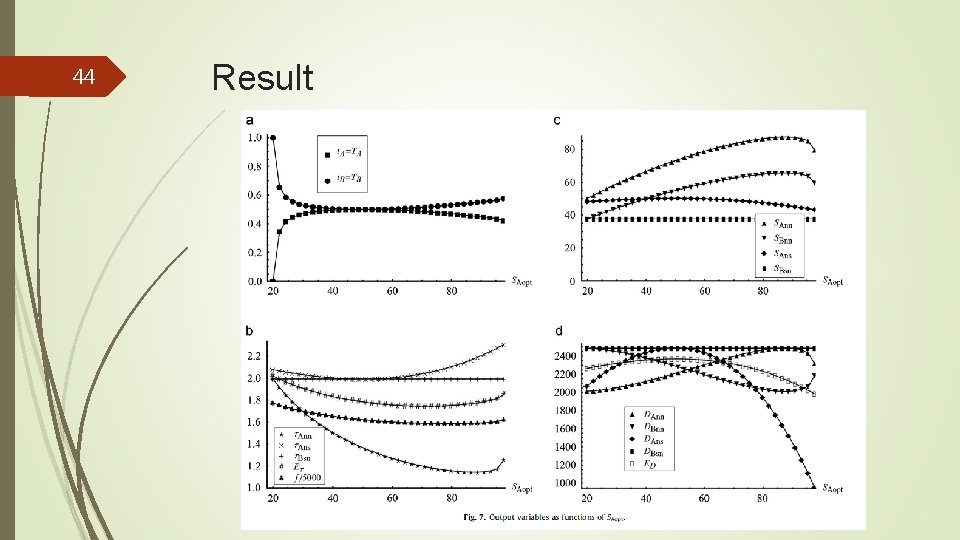
41 Result

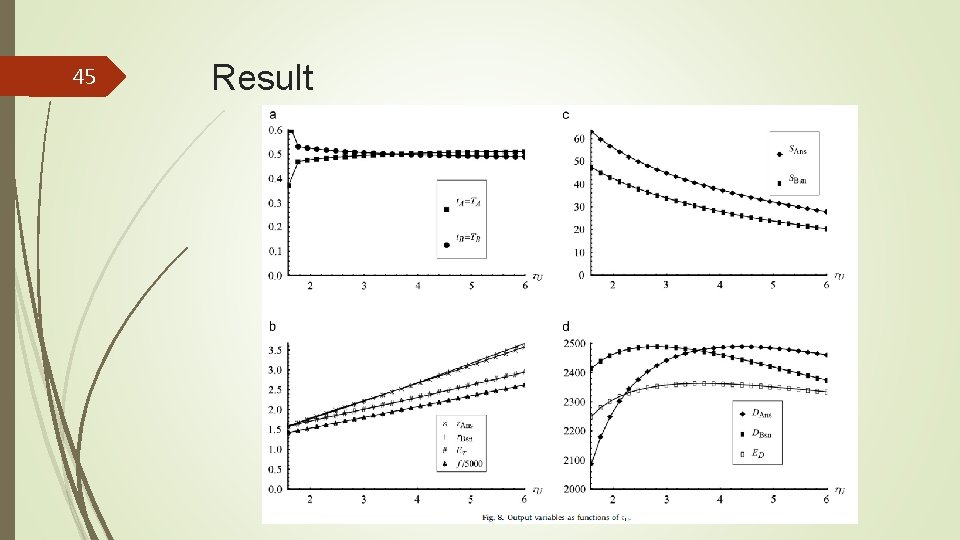
42 Result

43 Result

44 Result

45 Result

46 Agenda Introduction The model Results Conclusions

47 Conclusions To our knowledge, this is the first model of interdiction to explicitly consider congestion, rather than just increased travel distance. Although we consider a system of only two arcs, this is adequate for investigating some basic congestion phenomena. In our model, each of a population of drivers chooses the more time-efficient of two arcs of different lengths. Both arcs are subject to traffic congestion, and also to interdiction by an attacking terrorist. The players consist of the government, the terrorist, and the drivers. The government allocates a fixed resource to protect travel along the two arcs, while the terrorist allocates a fixed resource to interdict travel along the two arcs. The drivers choose the arc that gives the shortest travel time, and cannot choose a blocked arc.

48 Conclusions While the model is simple, with only two arcs, we provide interesting results. For example, our paper suggests that greater defensive effort should be allocated to less congested arcs (with faster travel times), and to routes with greater maximum travel density (e. g. , wider or straighter roads). Future research should extend this basic approach to networks with more than two arcs, and possibly also additional models of congestion. However, we believe that our results, while simple, help to pave the way for more realistic models of interdiction that consider congestion. Additional extensions may also be desirable, of course; for example, allowing the terrorist to attack different arcs in the system sequentially rather than simultaneously, thus making it possible for the terrorist to observe whether earlier attacks were successful before determining where to direct subsequent attacks.

Thanks for your attention