Deep Learning Exploiting Unlabeled Data Hungyi Lee Introduction

Deep Learning Exploiting Unlabeled Data Hung-yi Lee

Introduction • You already learn some machine learning techniques. • With labelled data, you can do any thing (hopefully). • Labelling data is expensive. • How to exploit unlabeled data? • Introduce two approaches • Restricted Boltzmann Machine (RBM) • Auto-encoder

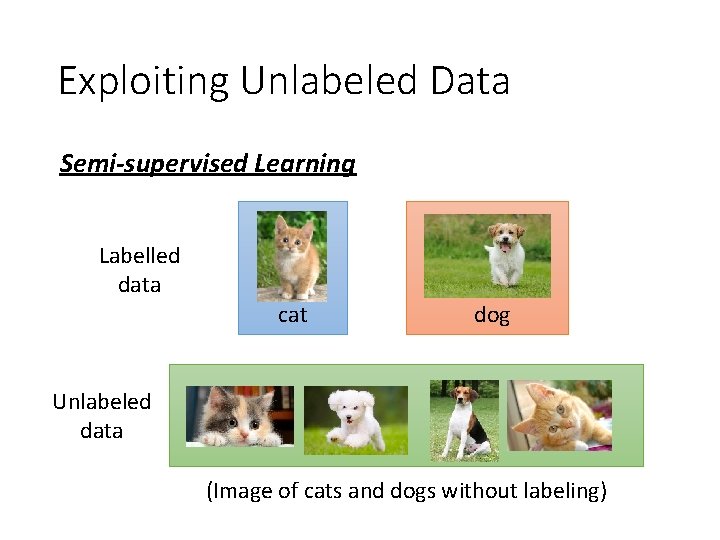
Exploiting Unlabeled Data Semi-supervised Learning Labelled data cat dog Unlabeled data (Image of cats and dogs without labeling)

Exploiting Unlabeled Data • Why semi-supervised learning helps? The distribution of the unlabeled data tell us something.

Exploiting Unlabeled Data • Sometimes unlabeled data is not related to the task. Labelled data cat dog Unlabeled data (Just crawl millions of images from the Internet)

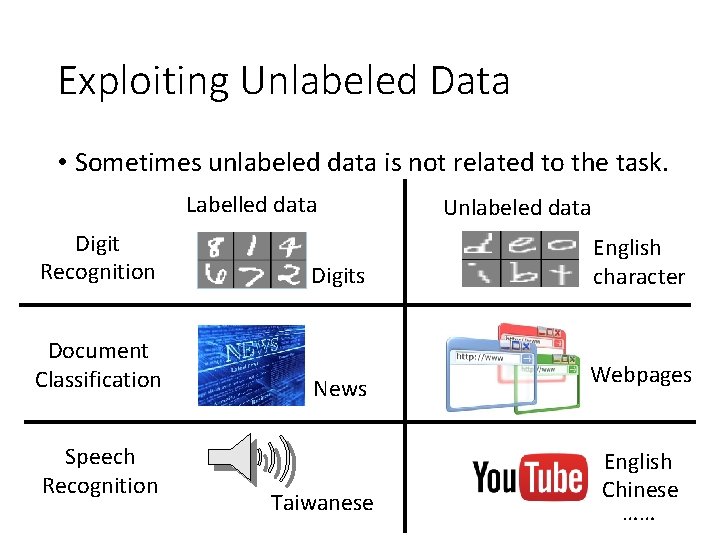
Exploiting Unlabeled Data • Sometimes unlabeled data is not related to the task. Labelled data Digit Recognition Document Classification Speech Recognition Digits News Taiwanese Unlabeled data English character Webpages English Chinese ……

Exploiting Unlabeled Data • How could unrelated unlabeled data help? Understand the nature of things The hand written images are composed of strokes ……. No. 1 No. 2 No. 3 No. 4 No. 5

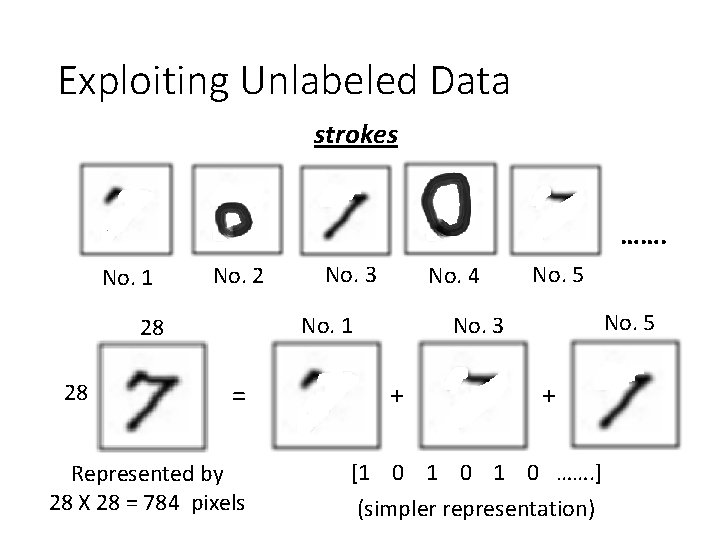
Exploiting Unlabeled Data strokes ……. No. 1 No. 2 No. 4 = Represented by 28 X 28 = 784 pixels No. 5 No. 3 No. 1 28 28 No. 3 + + [1 0 1 0 ……. ] (simpler representation)

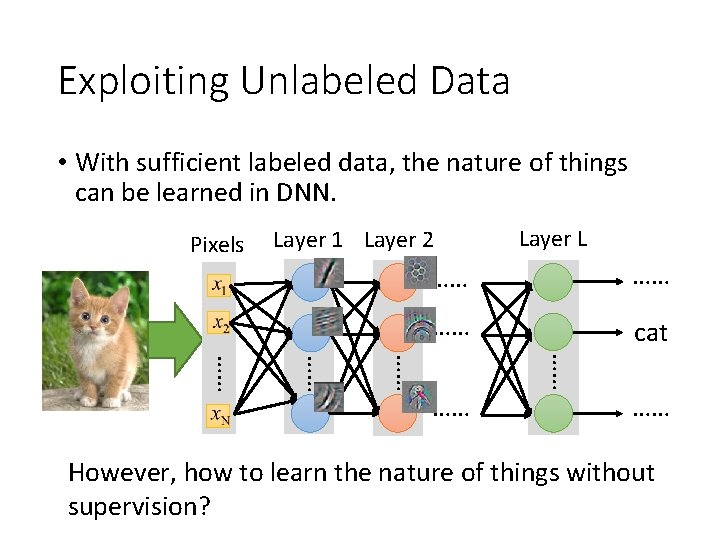
Exploiting Unlabeled Data • With sufficient labeled data, the nature of things can be learned in DNN. Pixels Layer 1 Layer 2 Layer L …… …… …… cat …… …… …… However, how to learn the nature of things without supervision?

Restricted Boltzmann Machine (RBM)

Where are we? Restricted Boltzmann Machine Undirected Graph (MRF, factor graph, etc. ) Graphical Model Structured Learning

Boltzmann Machine • Evaluation function

Boltzmann Machine - Example Probability Point of View

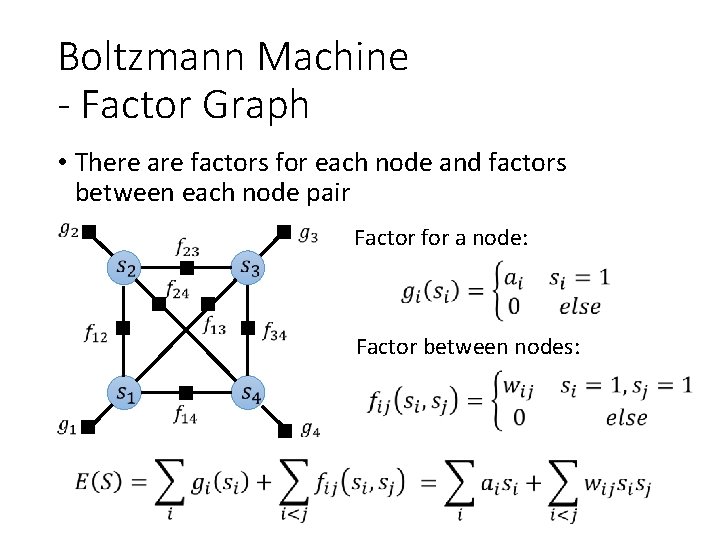
Boltzmann Machine - Factor Graph • There are factors for each node and factors between each node pair Factor for a node: Factor between nodes:

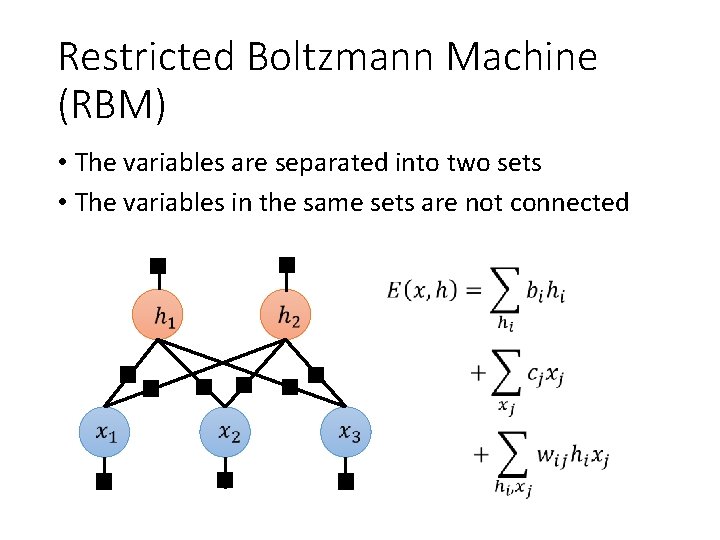
Restricted Boltzmann Machine (RBM) • The variables are separated into two sets • The variables in the same sets are not connected

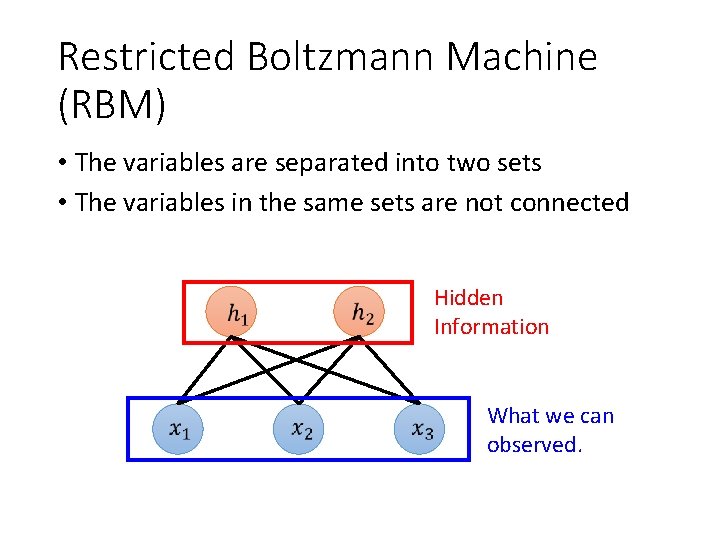
Restricted Boltzmann Machine (RBM) • The variables are separated into two sets • The variables in the same sets are not connected Hidden Information What we can observed.

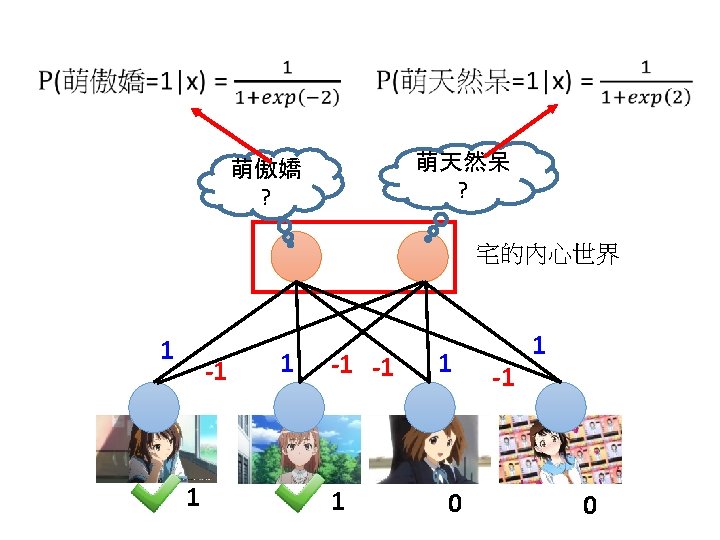
Restricted Boltzmann Machine (RBM) 宅A 宅B 宅C The world we observed. (Some combination is rare)

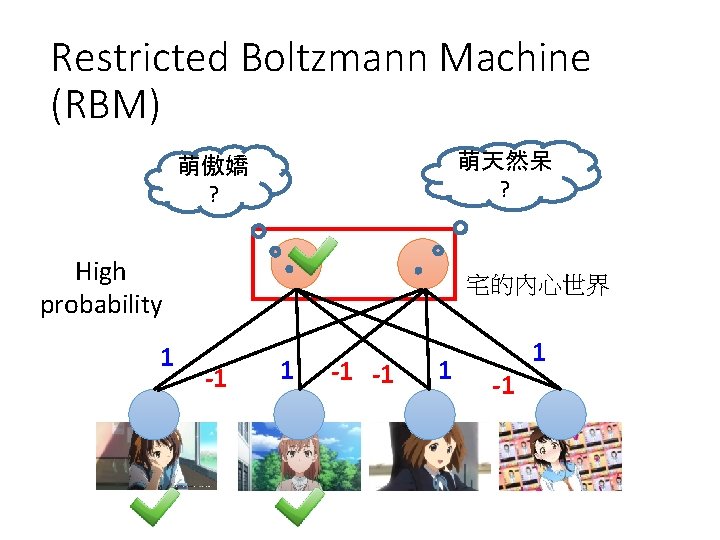
Restricted Boltzmann Machine (RBM) 萌天然呆 ? 萌傲嬌 ? High probability 1 宅的內心世界 -1 1

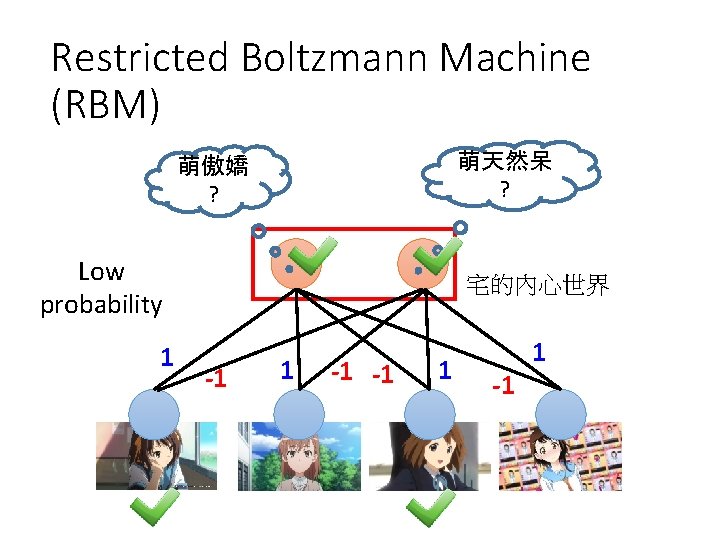
Restricted Boltzmann Machine (RBM) 萌天然呆 ? 萌傲嬌 ? Low probability 1 宅的內心世界 -1 1

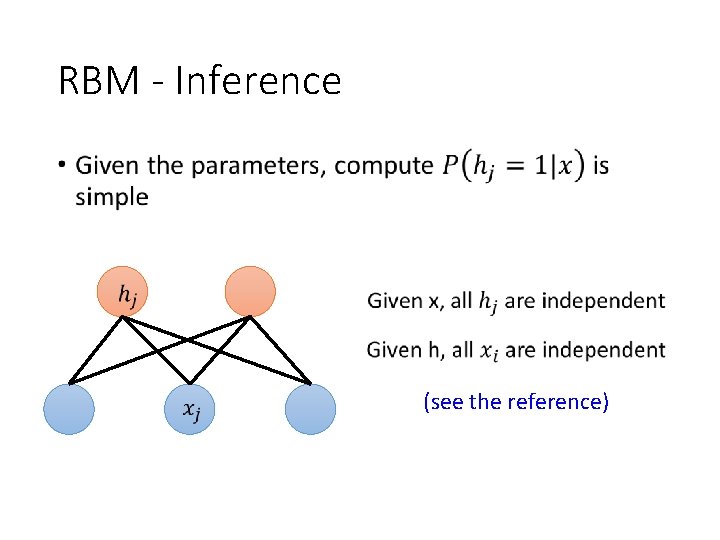
RBM - Inference • (see the reference)

RBM •

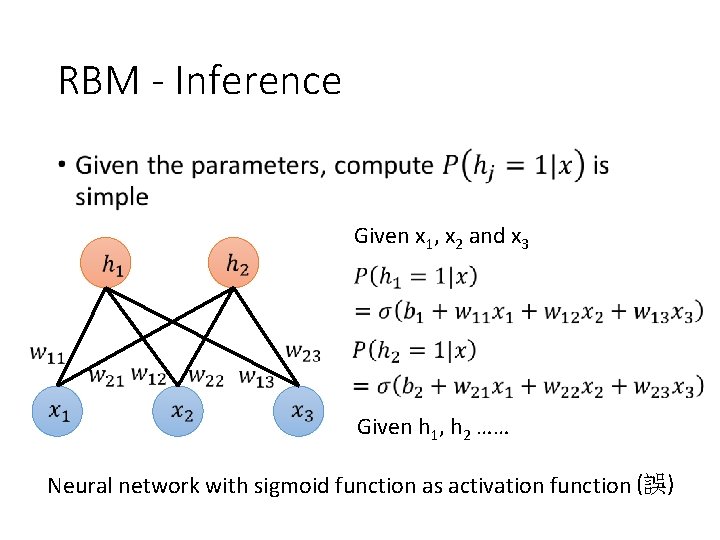
RBM - Inference • Given x 1, x 2 and x 3 Given h 1, h 2 …… Neural network with sigmoid function as activation function (誤)

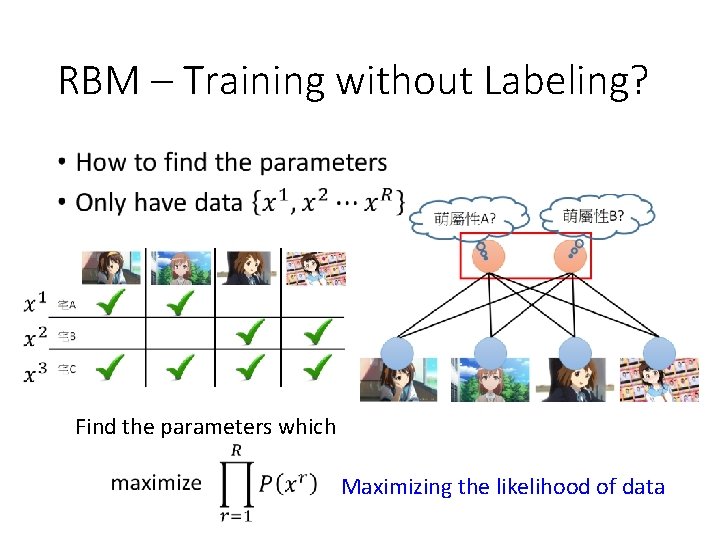
RBM – Training without Labeling? • Find the parameters which Maximizing the likelihood of data

RBM – Training without Labeling? • Intuition of maximizing P(x) (see the reference)

RBM – Training without Labeling? Soft. Plus Re. LU

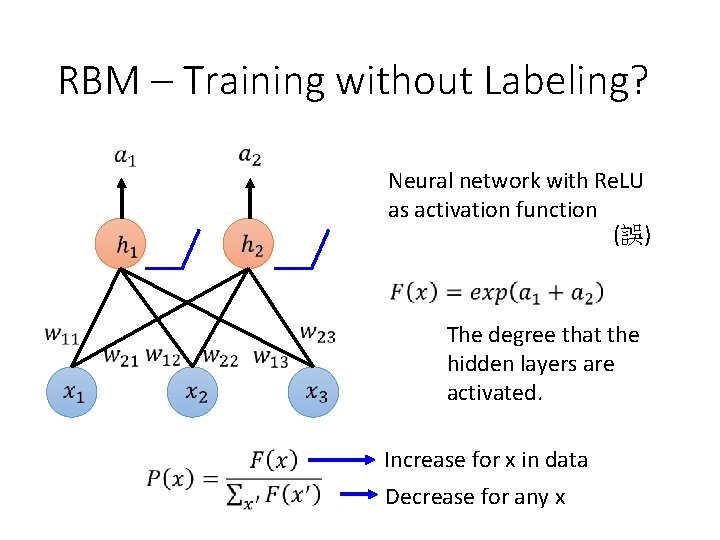
RBM – Training without Labeling? Neural network with Re. LU as activation function (誤) The degree that the hidden layers are activated. Increase for x in data Decrease for any x

RBM – Training by Gradient Ascent • compute

A B

A B

A B

A B

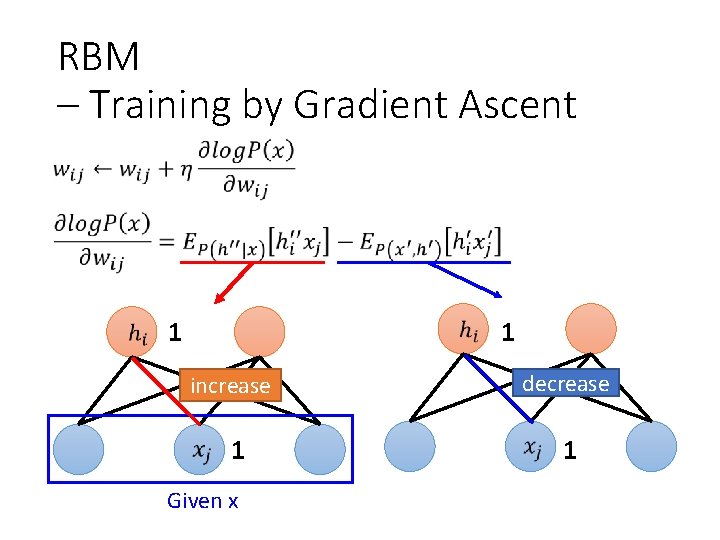
RBM – Training by Gradient Ascent 1 1 increase decrease 1 1 Given x

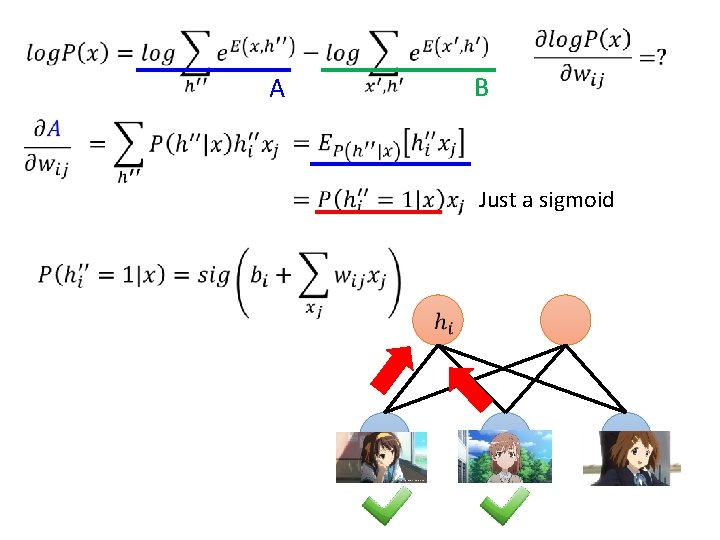
A B Just a sigmoid

B A Just a sigmoid Exact computing is not tractable …… Sample by Gibbs sampling

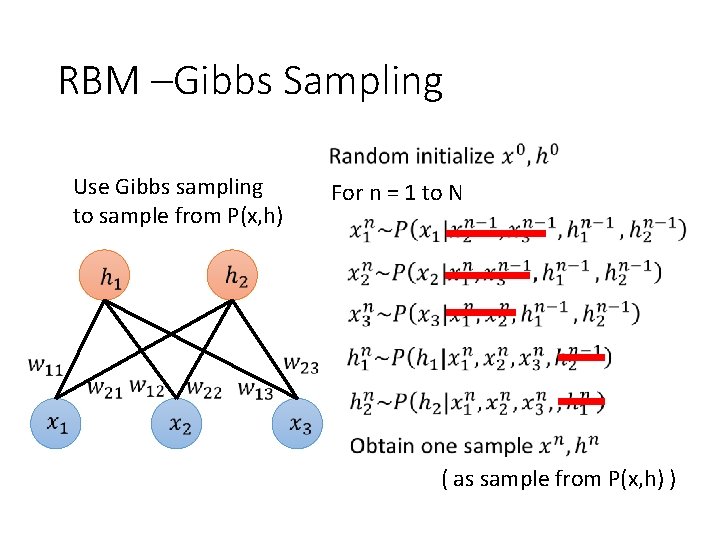
RBM –Gibbs Sampling Use Gibbs sampling to sample from P(x, h) For n = 1 to N ( as sample from P(x, h) )

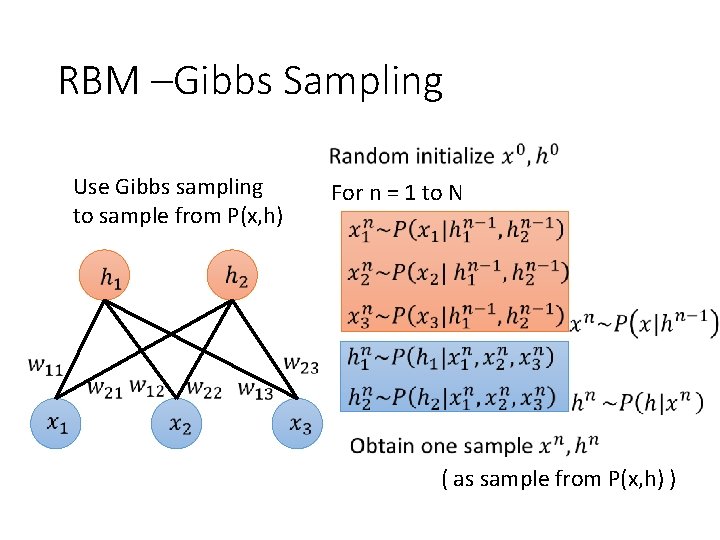
RBM –Gibbs Sampling Use Gibbs sampling to sample from P(x, h) For n = 1 to N ( as sample from P(x, h) )

RBM –Gibbs Sampling Each time we update parameters, we should do Gibbs sampling? !

RBM – Contrastive Divergence (CD) Stop! It works in reality! Persistent CD Ref: Tieleman, Tijmen. "Training restricted Boltzmann machines using approximations to the likelihood gradient. " Proceedings of the 25 th international conference on Machine learning. ACM, 2008.

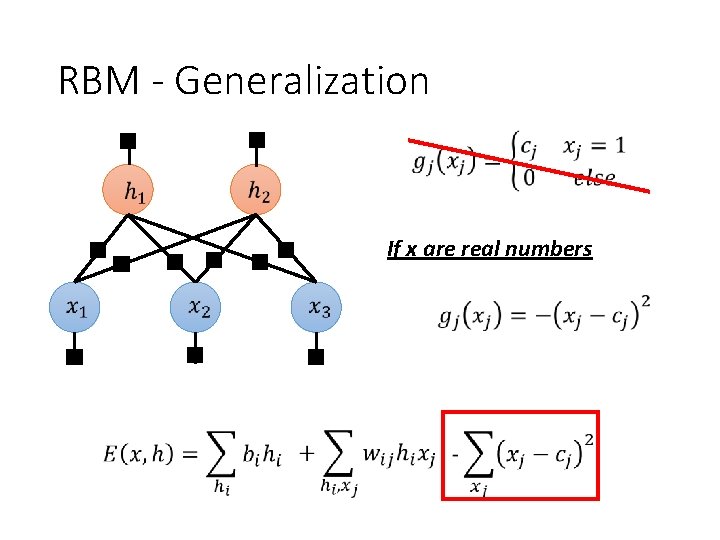
RBM - Generalization If x are real numbers

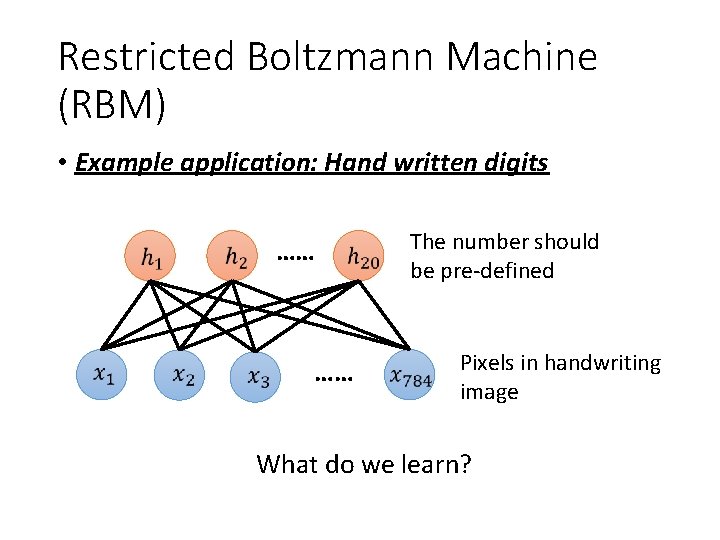
Restricted Boltzmann Machine (RBM) • Example application: Hand written digits …… …… The number should be pre-defined Pixels in handwriting image What do we learn?

RBM – Training without Labeling? Source of image: Larochelle, H. , Bengio, Y. , Louradour, J. , & Lamblin, P. (2009). Exploring strategies for training deep neural networks. The Journal of Machine Learning Research, 10, 1 -40.

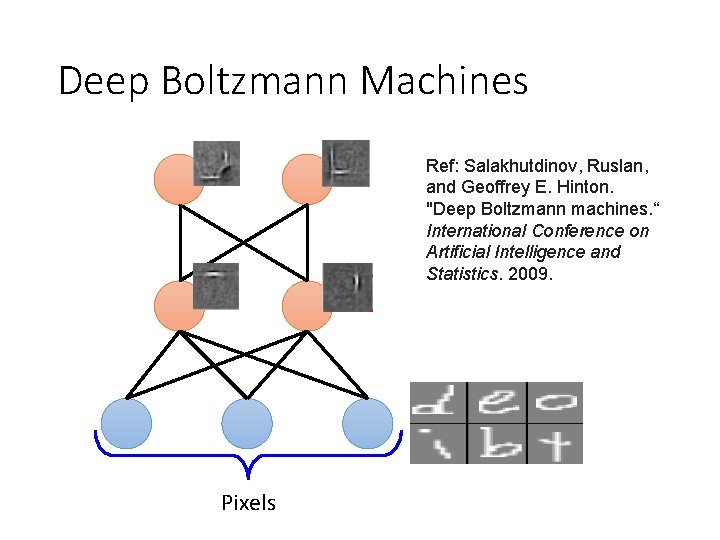
Deep Boltzmann Machines Ref: Salakhutdinov, Ruslan, and Geoffrey E. Hinton. "Deep Boltzmann machines. “ International Conference on Artificial Intelligence and Statistics. 2009. Pixels

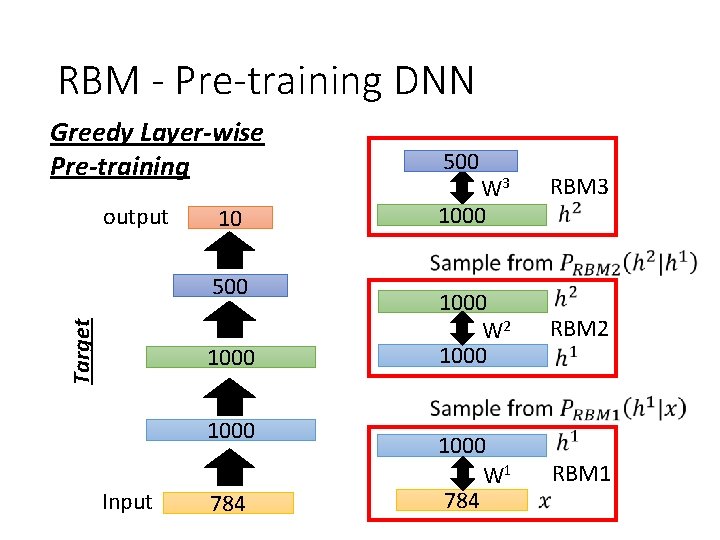
RBM - Pre-training DNN Greedy Layer-wise Pre-training output 10 Target 500 1000 Input 784 500 W 3 1000 RBM 3 1000 W 2 1000 RBM 2 1000 W 1 784 RBM 1

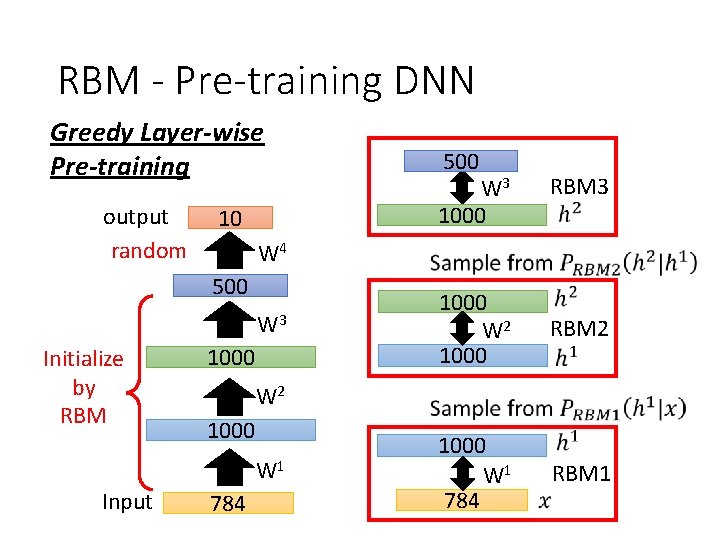
RBM - Pre-training DNN Greedy Layer-wise Pre-training output random 10 W 3 1000 RBM 3 1000 W 2 1000 RBM 2 1000 W 1 784 RBM 1 W 2 1000 W 1 Input W 3 1000 W 4 500 Initialize by RBM 500 784

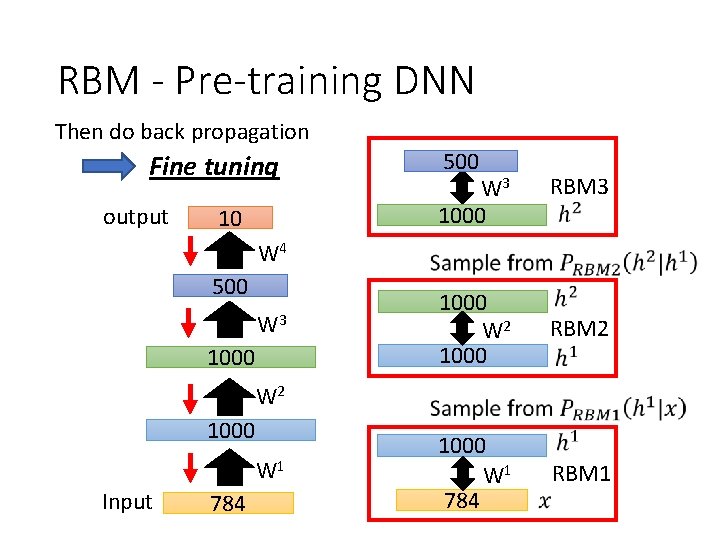
RBM - Pre-training DNN Then do back propagation Fine tuning output 10 500 W 3 1000 RBM 3 W 4 500 W 3 1000 W 2 1000 RBM 2 1000 W 1 784 RBM 1 W 2 1000 W 1 Input 784

More • RBM • Independent • https: //www. youtube. com/watch? v=lek. Ch_i 32 i. E&lis t=PL 6 Xpj 9 I 5 q. XYEc. Ohn 7 Tqgh. AJ 6 NAPr. Nm. UBH&index =37 • Neural networks [5. 2] : Restricted Boltzmann machine - inference • Intuition for maximizing likelihood • https: //www. youtube. com/watch? v=e 0 Ts_7 Y 6 h. ZU& list=PL 6 Xpj 9 I 5 q. XYEc. Ohn 7 Tqgh. AJ 6 NAPr. Nm. UBH&ind ex=38 • Neural networks [5. 3] : Restricted Boltzmann machine - free energy

More • DBN • https: //www. youtube. com/watch? v=vkb 6 AWYXZ 5 I&list =PL 6 Xpj 9 I 5 q. XYEc. Ohn 7 Tqgh. AJ 6 NAPr. Nm. UBH&index=57 • Neural networks [7. 7] : Deep learning - deep belief network • https: //www. youtube. com/watch? v=p. St. Dsc. Jh 2 Wo&list =PL 6 Xpj 9 I 5 q. XYEc. Ohn 7 Tqgh. AJ 6 NAPr. Nm. UBH&index=58 • Neural networks [7. 8] : Deep learning - variational bound • https: //www. youtube. com/watch? v=35 MUl. YCColk&list =PL 6 Xpj 9 I 5 q. XYEc. Ohn 7 Tqgh. AJ 6 NAPr. Nm. UBH&index=59 • Neural networks [7. 9] : Deep learning - DBN pretraining

Auto-encoder

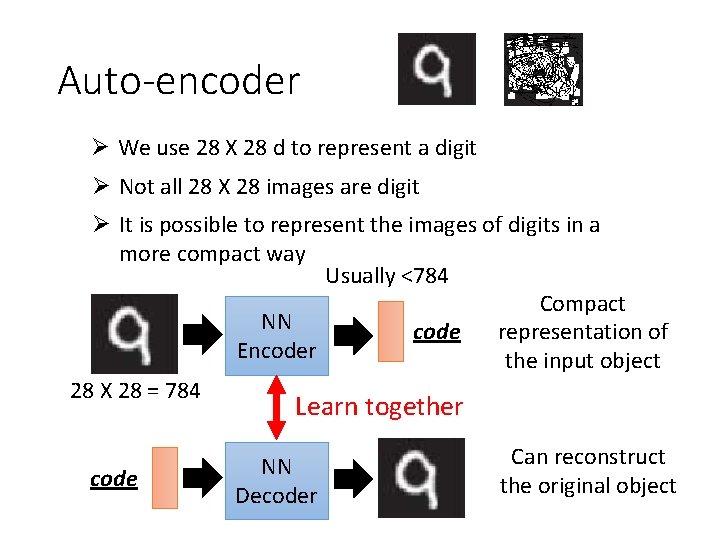
Auto-encoder Ø We use 28 X 28 d to represent a digit Ø Not all 28 X 28 images are digit Ø It is possible to represent the images of digits in a more compact way Usually <784 Compact NN representation of code Encoder the input object 28 X 28 = 784 Learn together code NN Decoder Can reconstruct the original object

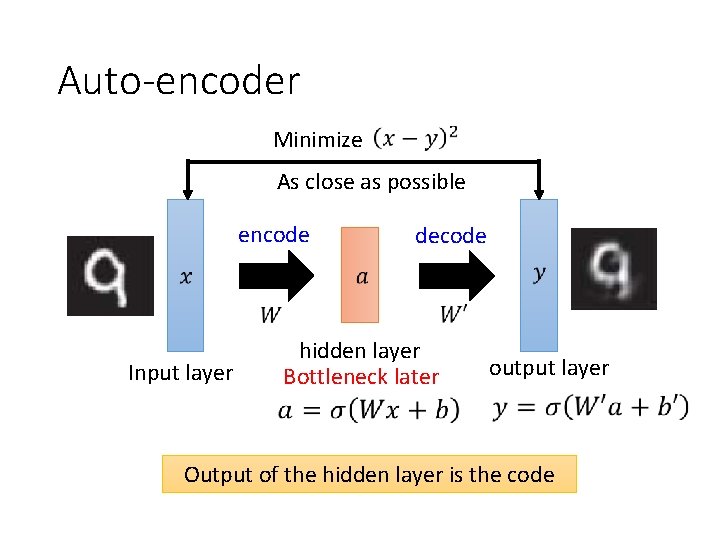
Auto-encoder Minimize As close as possible encode Input layer decode hidden layer Bottleneck later output layer Output of the hidden layer is the code

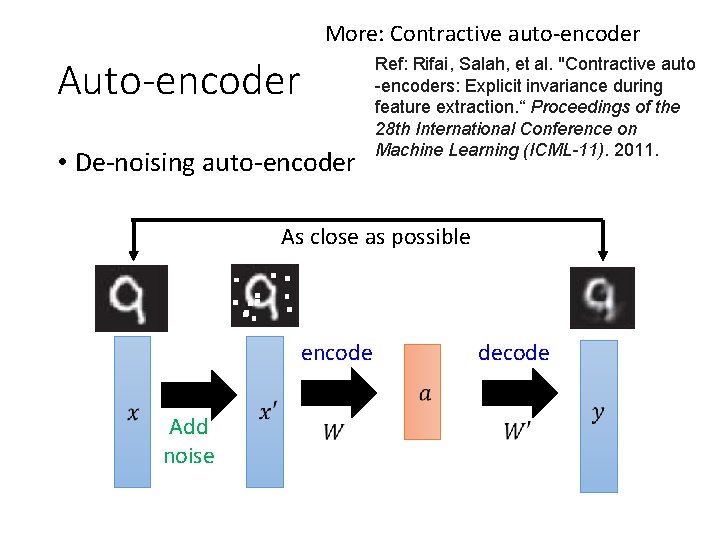
More: Contractive auto-encoder Auto-encoder • De-noising auto-encoder Ref: Rifai, Salah, et al. "Contractive auto -encoders: Explicit invariance during feature extraction. “ Proceedings of the 28 th International Conference on Machine Learning (ICML-11). 2011. As close as possible encode Add noise decode

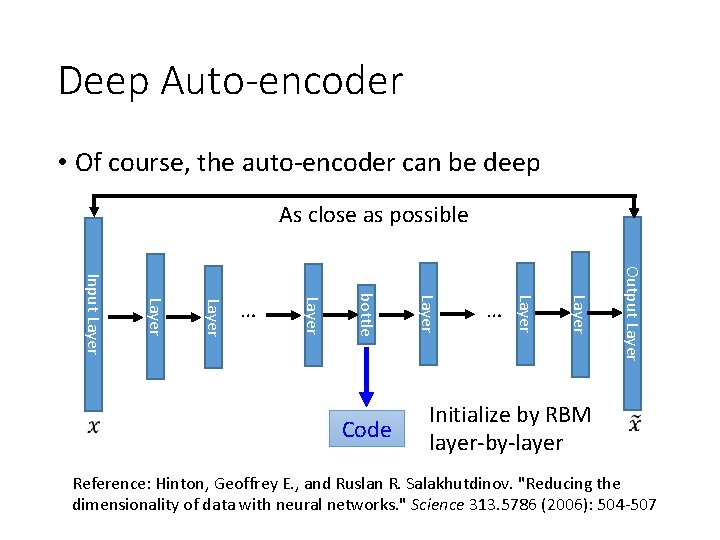
Deep Auto-encoder • Of course, the auto-encoder can be deep As close as possible Output Layer … Layer Code Layer bottle Layer Input Layer … Initialize by RBM layer-by-layer Reference: Hinton, Geoffrey E. , and Ruslan R. Salakhutdinov. "Reducing the dimensionality of data with neural networks. " Science 313. 5786 (2006): 504 -507

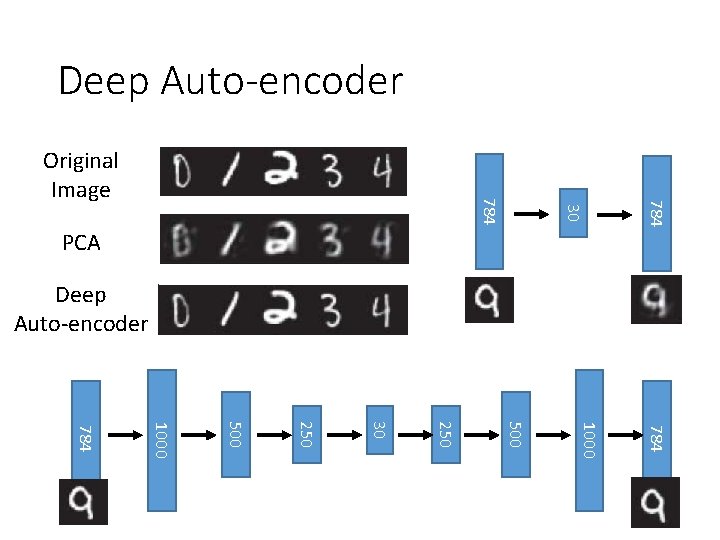
Deep Auto-encoder 784 30 784 Original Image PCA Deep Auto-encoder 784 1000 500 250 30 250 500 1000 784

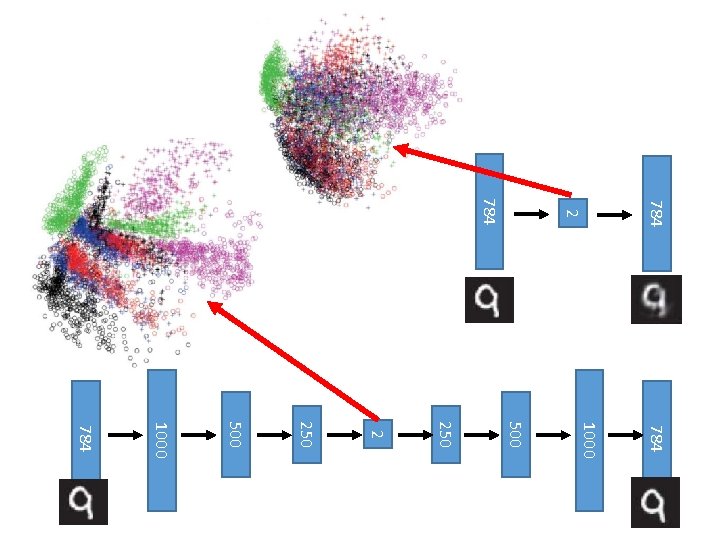
784 2 784 1000 500 250 2 250 500 1000 784

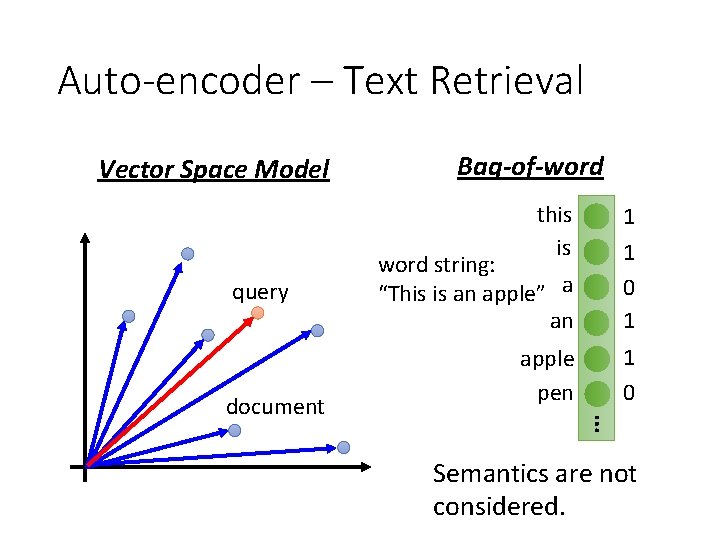
Auto-encoder – Text Retrieval Vector Space Model query this is word string: “This is an apple” a an 1 1 0 1 apple pen 1 0 … document Bag-of-word Semantics are not considered.

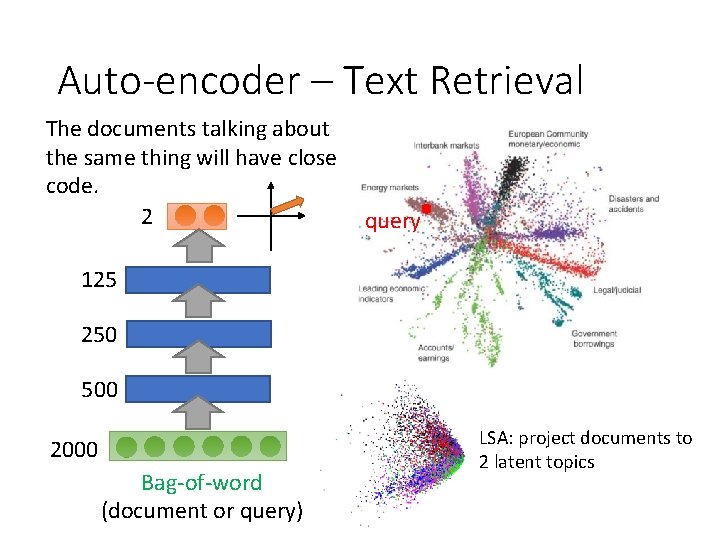
Auto-encoder – Text Retrieval The documents talking about the same thing will have close code. 2 query 125 250 500 2000 Bag-of-word (document or query) LSA: project documents to 2 latent topics

Auto-encoder – Similar Image Search Retrieved using Euclidean distance in pixel intensity space (Images from Hinton’s slides on Coursera) Reference: Krizhevsky, Alex, and Geoffrey E. Hinton. "Using very deep autoencoders for content-based image retrieval. " ESANN. 2011.

Auto-encoder – Similar Image Search code (crawl millions of images from the Internet) 256 512 1024 2048 4096 8192 32 x 32

Retrieved using Euclidean distance in pixel intensity space retrieved using 256 codes

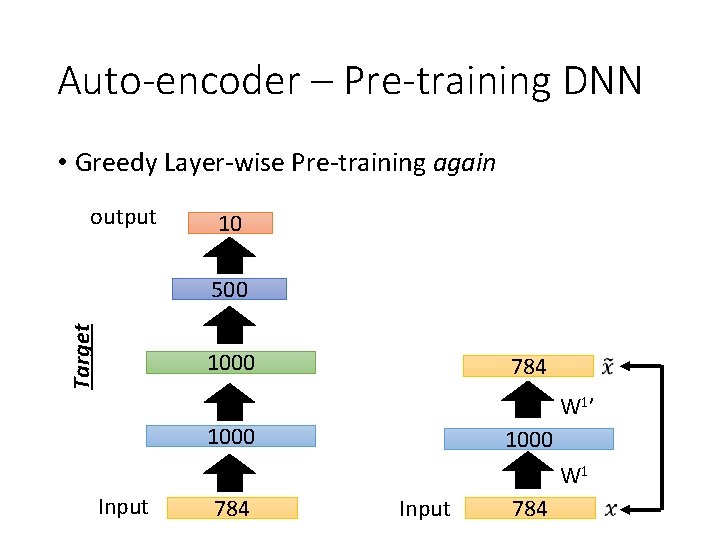
Auto-encoder – Pre-training DNN • Greedy Layer-wise Pre-training again output 10 Target 500 1000 784 W 1’ 1000 W 1 Input 784

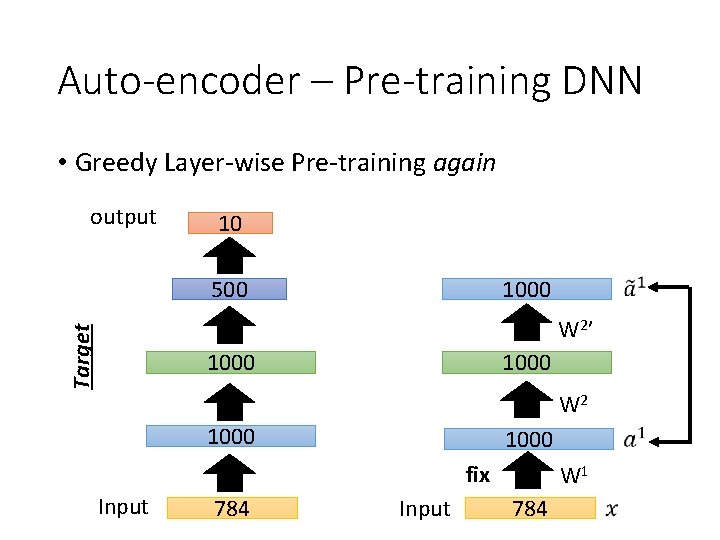
Auto-encoder – Pre-training DNN • Greedy Layer-wise Pre-training again output 10 500 1000 Target W 2’ 1000 W 2 1000 fix Input 784 Input W 1 784

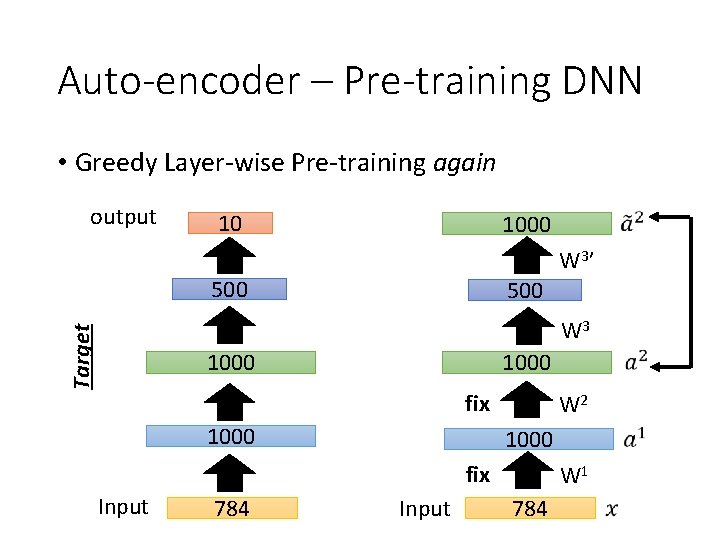
Auto-encoder – Pre-training DNN • Greedy Layer-wise Pre-training again output 10 1000 W 3’ 500 Target W 3 1000 fix 1000 W 2 1000 fix Input 784 Input W 1 784

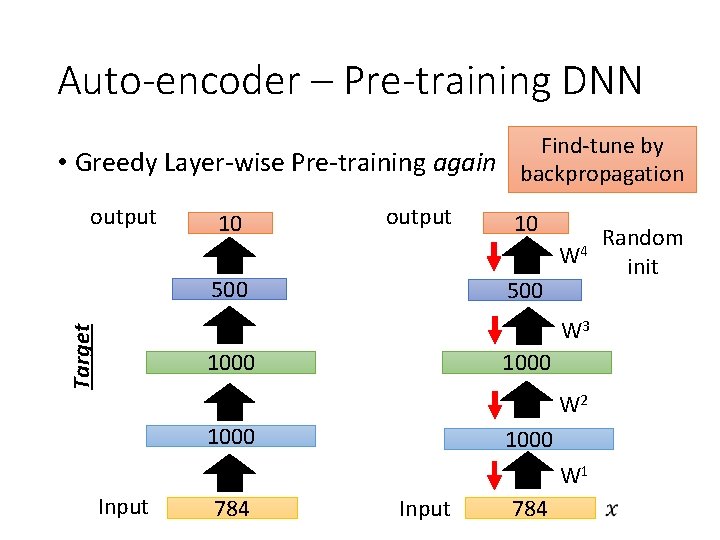
Auto-encoder – Pre-training DNN Find-tune by • Greedy Layer-wise Pre-training again backpropagation output 10 W 4 500 Target W 3 1000 W 2 1000 W 1 Input 784 Random init

Concluding Remarks

Concluding Remarks • Labeling data is expensive, but it is relatively easy to collect lots of unlabeled data. • RBM and auto-encoder exploit the unlabeled data • RBM and auto-encoder had been popular for pretraining DNN before. • With sufficient labelled data and Re. LU, pre-training is not that important. • However, it is still useful when you have lots of unlabeled data but little labelled data