Deep Image Homography Estimation Oct 8 2016 DongWon

Deep Image Homography Estimation Oct. 8, 2016 Dong-Won Shin D. De. Tone, T. Malisiewicz, and A. Rabinovich, “Deep Image Homography Estimation, ” Robotics: Science and Systems 2016, Workshop on Limits and Potentials of Deep Learning in Robotics

Contents • Introduction • Motivations • Contributions • Training Data Generation • Homography. Net • Experiment results • Conclusion 2

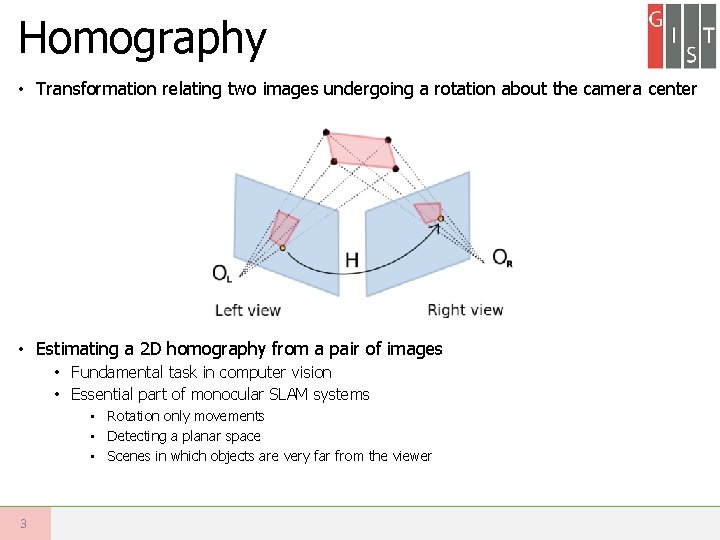
Homography • Transformation relating two images undergoing a rotation about the camera center • Estimating a 2 D homography from a pair of images • Fundamental task in computer vision • Essential part of monocular SLAM systems • Rotation only movements • Detecting a planar space • Scenes in which objects are very far from the viewer 3

Homography • Applications • Augmented Reality system based on planar structures and homographies • G. Simon, A. Fitzgibbon, and A. Zisserman. Markerless tracking using planar structures in the scene. In Proc. International Symposium on Augmented Reality, pages 120– 128, October 2000. • Camera calibration techniques using planar structures • Zhengyou Zhang. A flexible new technique for camera calibration. PAMI, 22(11): 1330– 1334, 2000. 4

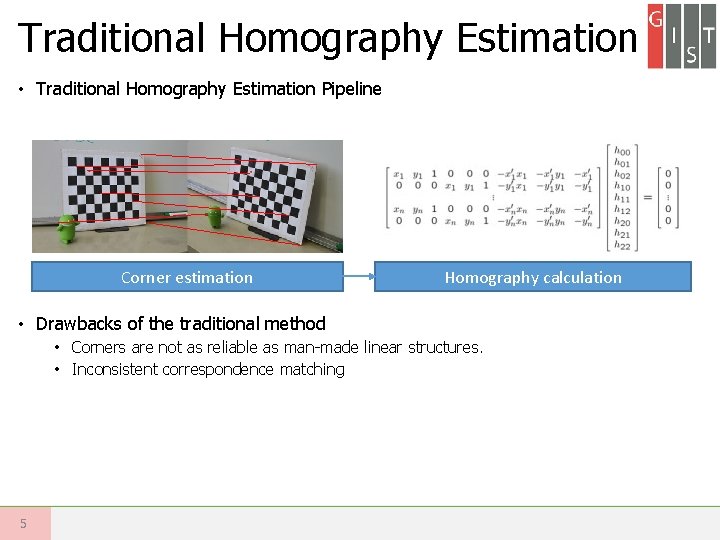
Traditional Homography Estimation • Traditional Homography Estimation Pipeline Corner estimation Homography calculation • Drawbacks of the traditional method • Corners are not as reliable as man-made linear structures. • Inconsistent correspondence matching 5

Objective • Given a pair of images, simply returns the homography relating the pair Instead of manually engineering corner-ish features, line-ish features, etc, is it possible for the algorithm to learn its own set of primitives? • Transformation estimation step as the last part of a deep learning pipeline • Ability to learn the entire homography estimation pipeline in an end-to-end fashion 6

Motivations • LSD-SLAM • Feature-less monocular SLAM algorithm • Promising results in using a full image for geometric computer vision tasks • Deep convolutional networks • state-of-the-art benchmarks in semantic tasks such as image classification, semantic segmentation and human pose estimation • Examples) Flow. Net, Deep Semantic Matching, Multi-Scale Deep Network • Promising results for dense geometric computer vision tasks like optical flow and depth estimation, and even robotic tasks like visual odometry 7 J. Engel, T. Sch¨ops, and D. Cremers. LSD-SLAM: Large-scale direct monocular SLAM. 2014. G. E. Hinton, S. Osindero, and Y. W. Teh, “A Fast Learning Algorithm for Deep Belief Nets. , ” Neural Computation, 2006.

Contributions • Homography estimation methodology using a deep convolutional neural network • Training data generation strategy • Creating a seemingly infinite dataset of training triplets • MS-COCO dataset (Microsoft Common Objects in Context) • Additional formulation of the homography estimation problem as classification 8 T. -Y. Lin, M. Maire, S. Belongie, J. Hays, Pietro Perona, D. Ramanan, P. Dollár, and C. L. Zitnick, “Microsoft COCO: Common Objects in Context, ” ar. Xiv. org, vol. cs. CV. 02 -May-2014.

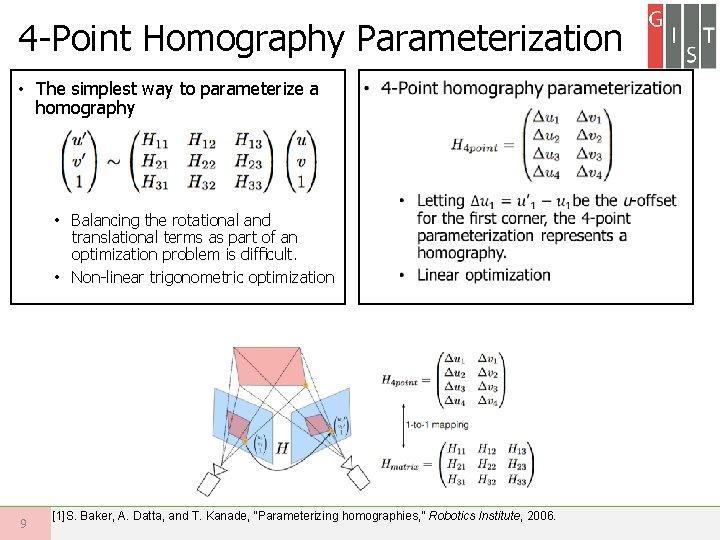
4 -Point Homography Parameterization • The simplest way to parameterize a homography • Balancing the rotational and translational terms as part of an optimization problem is difficult. • Non-linear trigonometric optimization 9 [1]S. Baker, A. Datta, and T. Kanade, “Parameterizing homographies, ” Robotics Institute, 2006.

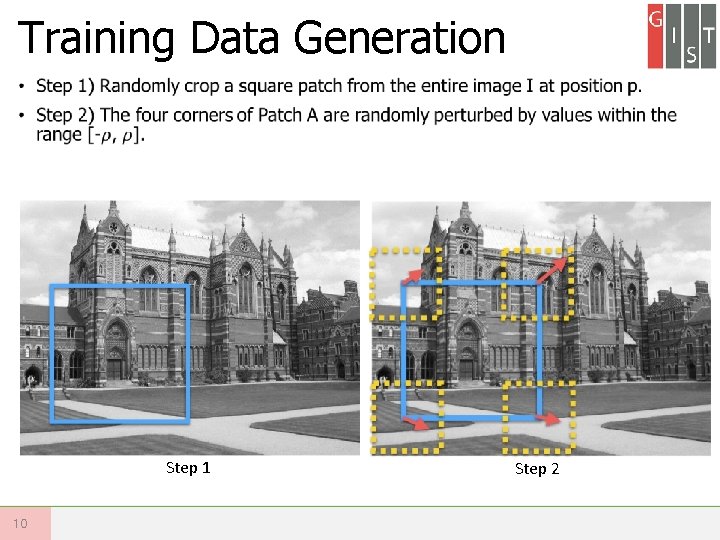
Training Data Generation • Step 1 10 Step 2

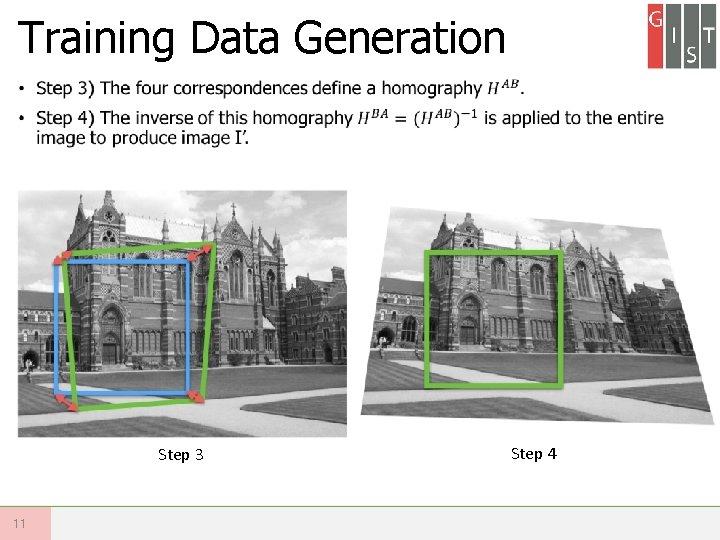
Training Data Generation • Step 3 11 Step 4

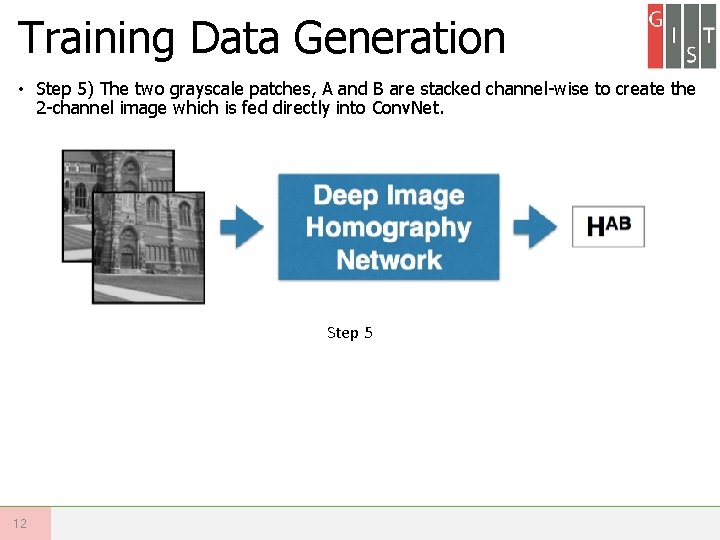
Training Data Generation • Step 5) The two grayscale patches, A and B are stacked channel-wise to create the 2 -channel image which is fed directly into Conv. Net. Step 5 12

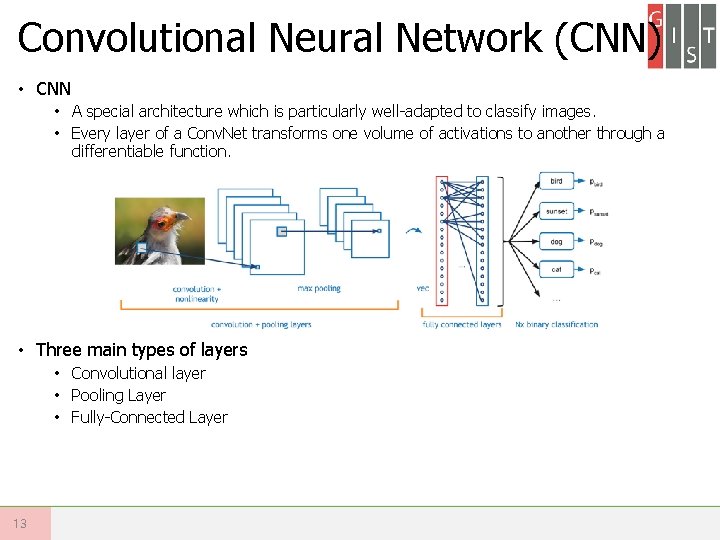
Convolutional Neural Network (CNN) • CNN • A special architecture which is particularly well-adapted to classify images. • Every layer of a Conv. Net transforms one volume of activations to another through a differentiable function. • Three main types of layers • Convolutional layer • Pooling Layer • Fully-Connected Layer 13

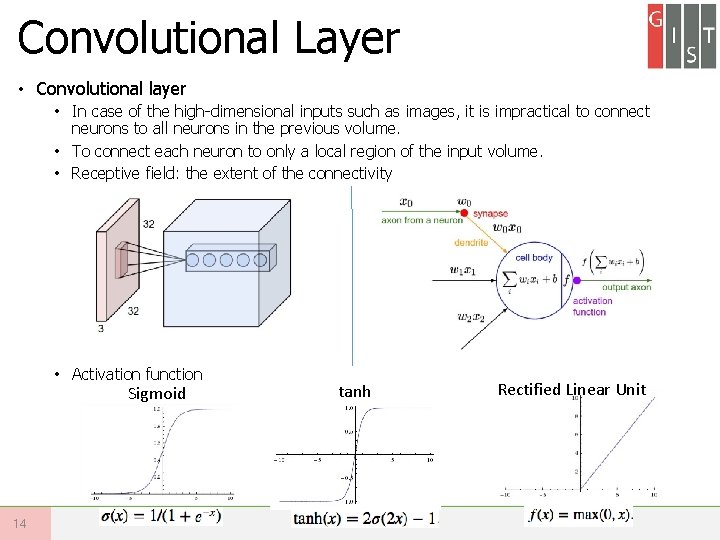
Convolutional Layer • Convolutional layer • In case of the high-dimensional inputs such as images, it is impractical to connect neurons to all neurons in the previous volume. • To connect each neuron to only a local region of the input volume. • Receptive field: the extent of the connectivity • Activation function Sigmoid 14 tanh Rectified Linear Unit

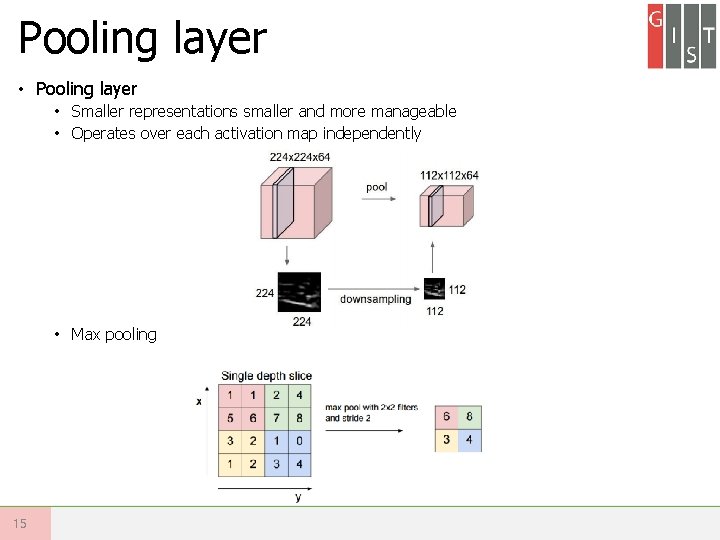
Pooling layer • Smaller representations smaller and more manageable • Operates over each activation map independently • Max pooling 15

Fully-connected layer • full connections to all activations in the previous layer, as seen in regular Neural Networks • computed with a matrix multiplication followed by a bias offset. 16

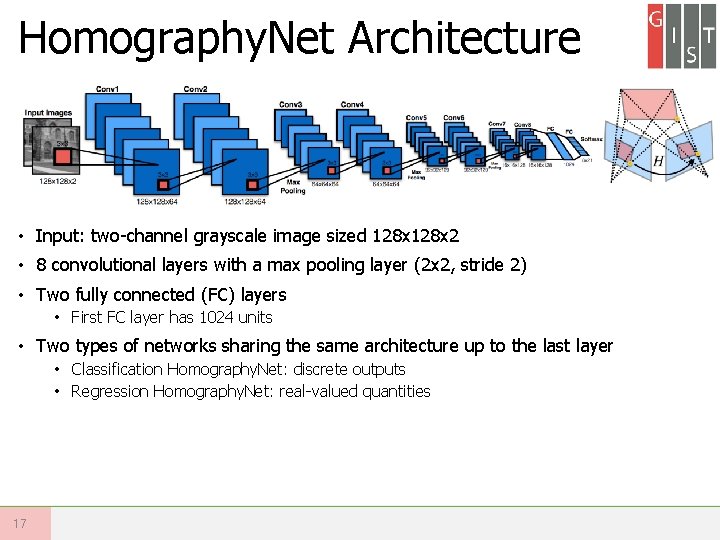
Homography. Net Architecture • Input: two-channel grayscale image sized 128 x 2 • 8 convolutional layers with a max pooling layer (2 x 2, stride 2) • Two fully connected (FC) layers • First FC layer has 1024 units • Two types of networks sharing the same architecture up to the last layer • Classification Homography. Net: discrete outputs • Regression Homography. Net: real-valued quantities 17

Regression Homography. Net • Directly produces 8 real-valued numbers • Euclidean (L 2) loss as the final layer during training • Pros: simplicity • Cons: such a direct approach could be prohibitive in certain applications. 18

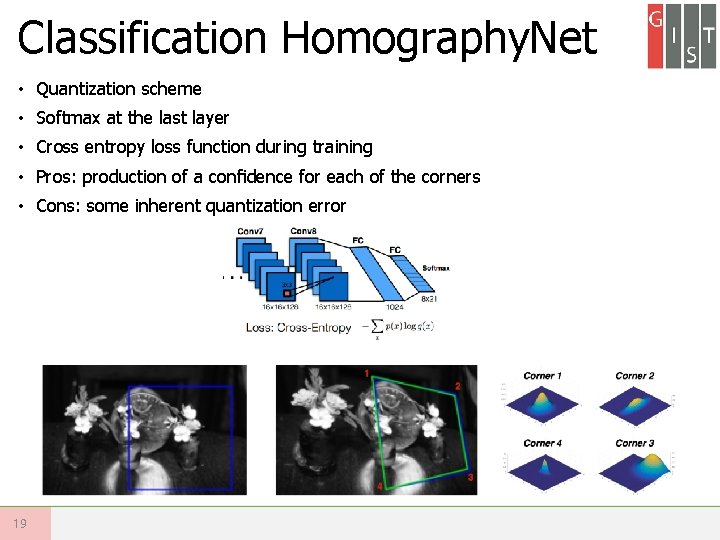
Classification Homography. Net • Quantization scheme • Softmax at the last layer • Cross entropy loss function during training • Pros: production of a confidence for each of the corners • Cons: some inherent quantization error 19

Experiments • 20

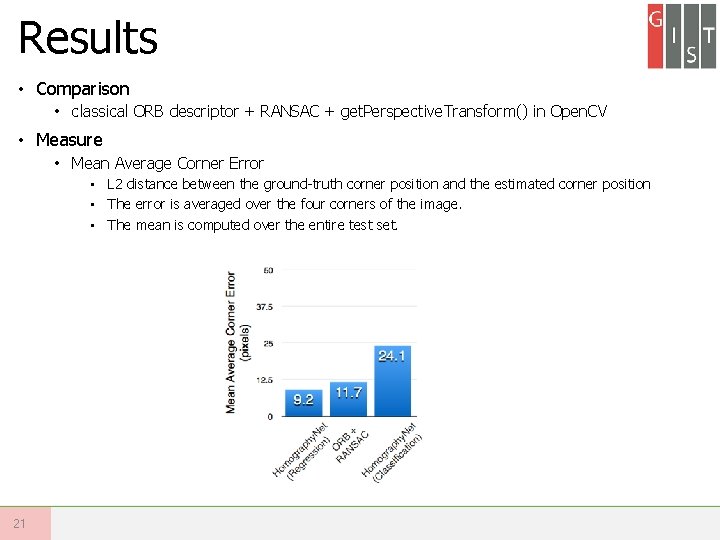
Results • Comparison • classical ORB descriptor + RANSAC + get. Perspective. Transform() in Open. CV • Measure • Mean Average Corner Error • L 2 distance between the ground-truth corner position and the estimated corner position • The error is averaged over the four corners of the image. • The mean is computed over the entire test set. 21

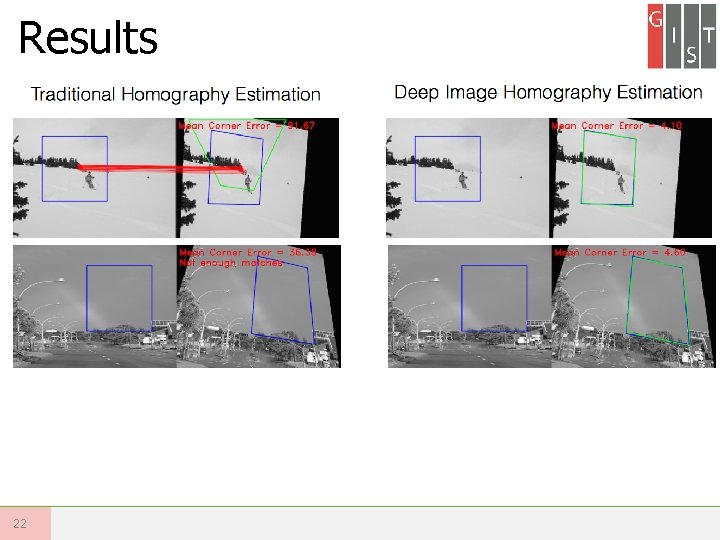
Results 22

Results 23

Applications • Advantages • Over 300 fps on an NVIDIA Titan X GPU • Light-weight • Robot that navigates an indoor floor using planar SLAM via homography estimation • Environment and sensor-specific noise, motion blur, and occlusions which might restrict the ability of a homography estimation algorithm can be tackled in a similar fashion using a Conv. Net. • Other classical computer vision tasks such as image mosaic • Markerless camera tracking systems for augmented reality 24

Conclusions • Homography. Net • End-to-end training pipeline contains two additional insights: • 4 -point corner parameterization of homographies • a large dataset of real image to create an seemingly unlimited-sized training set for homography estimation • More geometric problems in vision will be tackled using learning paradimes. 25