Deep Constrained Dominant Sets for Person ReIdentification Alemu

Deep Constrained Dominant Sets for Person Re-Identification Alemu Leulseged Tesfaye Marcello Pelillo Mubarak Shah

Overview Person Re-Identification Query Top Ranked Images

Challenges • Background clutter • Varying pose and view points • Illumination Changes • Occlusion

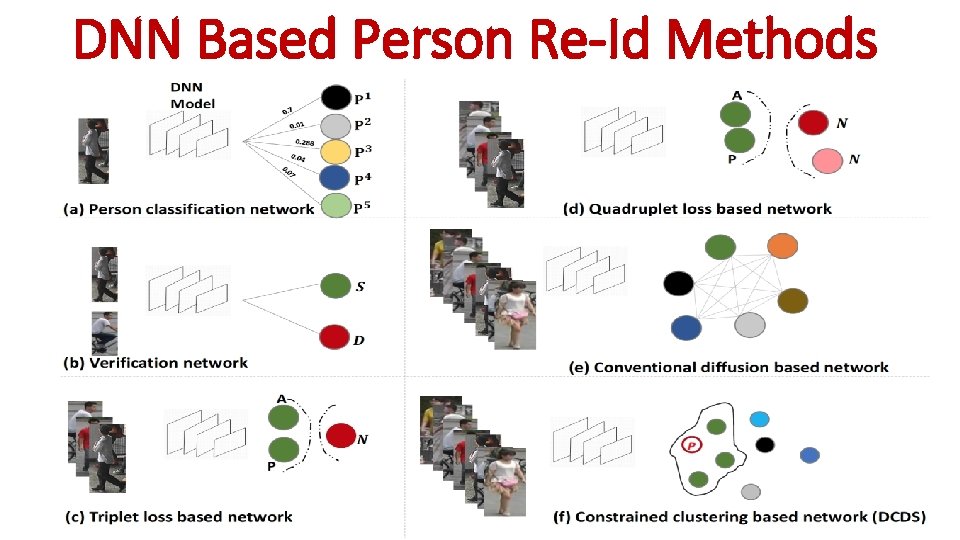
DNN Based Person Re-Id Methods

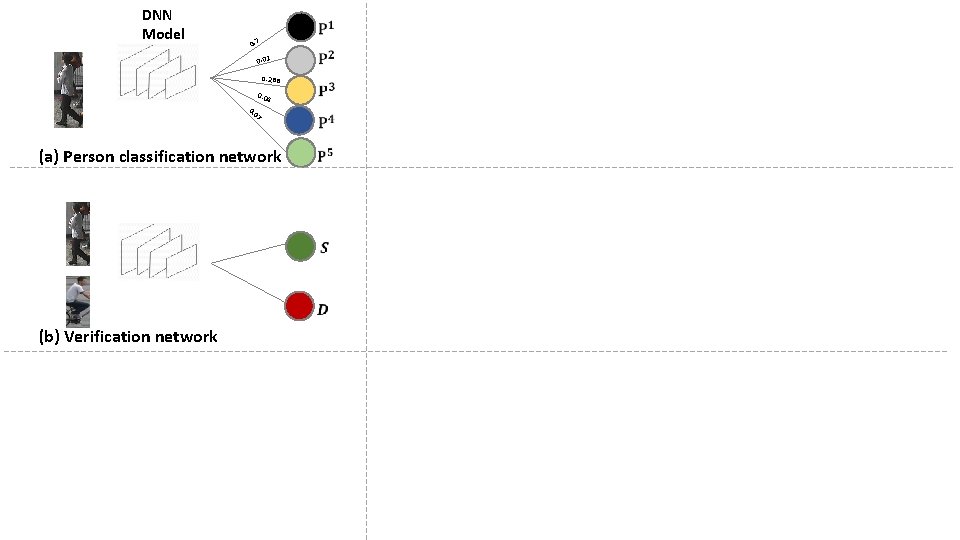
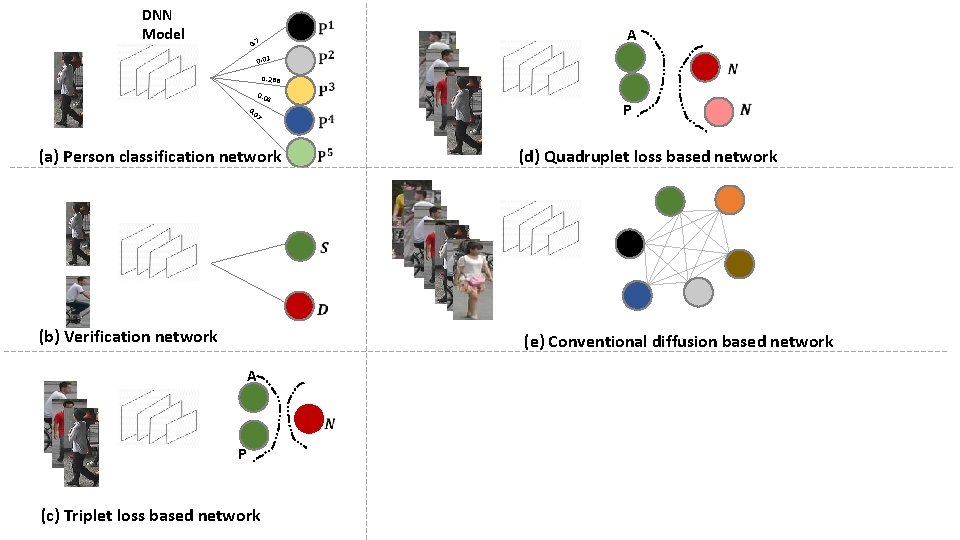
DNN Model 0. 7 0. 01 0. 288 0. 04 7 0 0. (a) Person classification network (b) Verification network

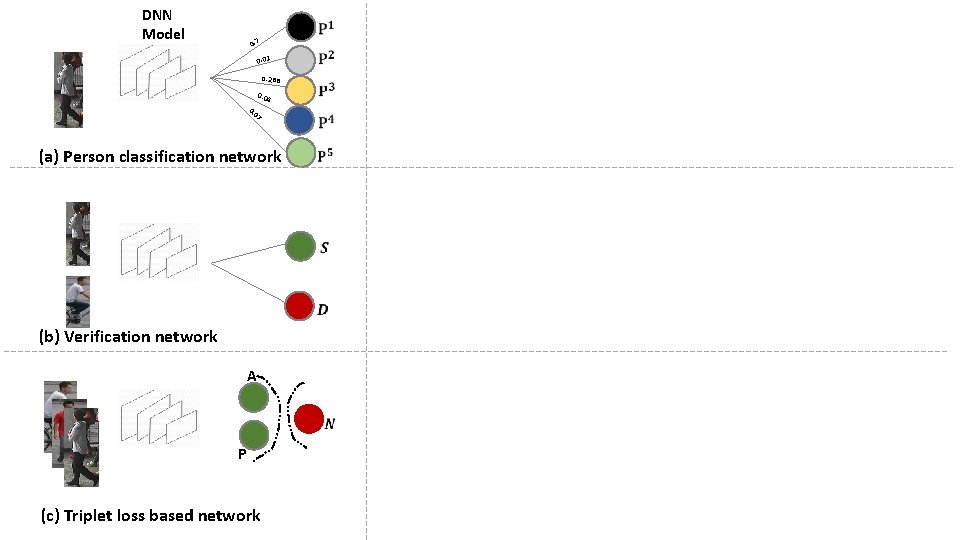
DNN Model 0. 7 0. 01 0. 288 0. 04 7 0 0. (a) Person classification network (b) Verification network A P (c) Triplet loss based network

Triplet Loss Based Network Positive Negative

Triplet Loss Based Network

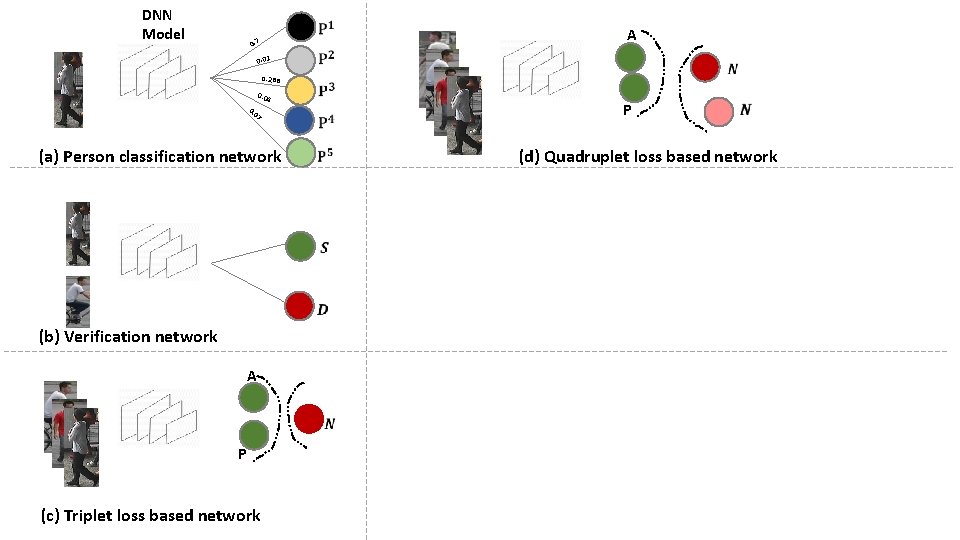
DNN Model 0. 7 0. 01 0. 288 0. 04 7 0 0. (a) Person classification network A P (d) Quadruplet loss based network (b) Verification network A P (c) Triplet loss based network

Quadruplet Loss Based Network

Quadruplet Loss Based Network

DNN Model 0. 7 0. 01 0. 288 0. 04 7 0 0. (a) Person classification network A P (d) Quadruplet loss based network (b) Verification network (e) Conventional diffusion based network A P (c) Triplet loss based network

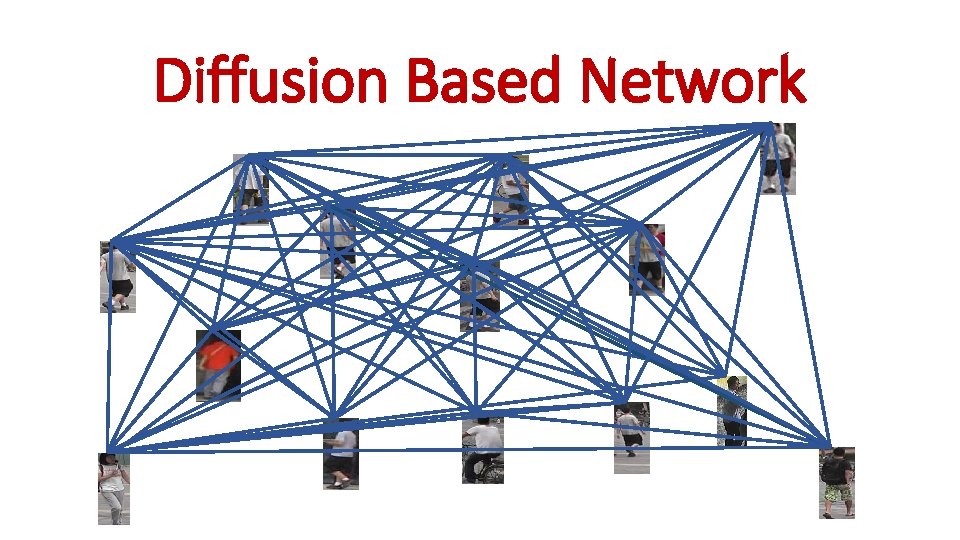
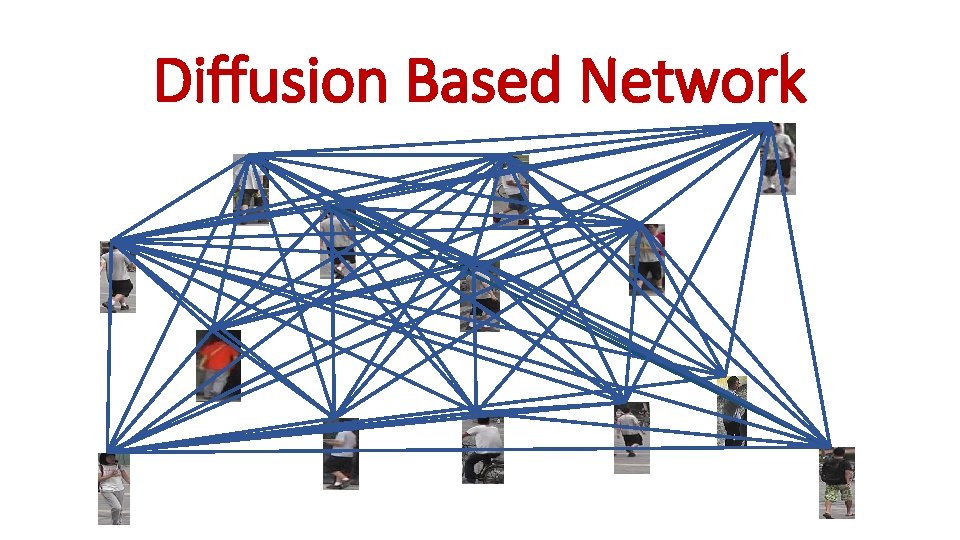
Diffusion Based Network (e) Conventional diffusion based network

Diffusion Based Network

Diffusion Based Network

Diffusion Based Network 0. 03 0. 06 0. 05 0. 13 0. 14 0. 11 0. 18 0. 006 0. 008 0. 11 0. 004 0. 12 0. 04 0. 01 Random Walk Probability

Diffusion Based Network (e) Conventional diffusion based network q. Exploit the contextual information between gallery images to provide a context sensitive similarity. q Do not apply probe image as a constraint

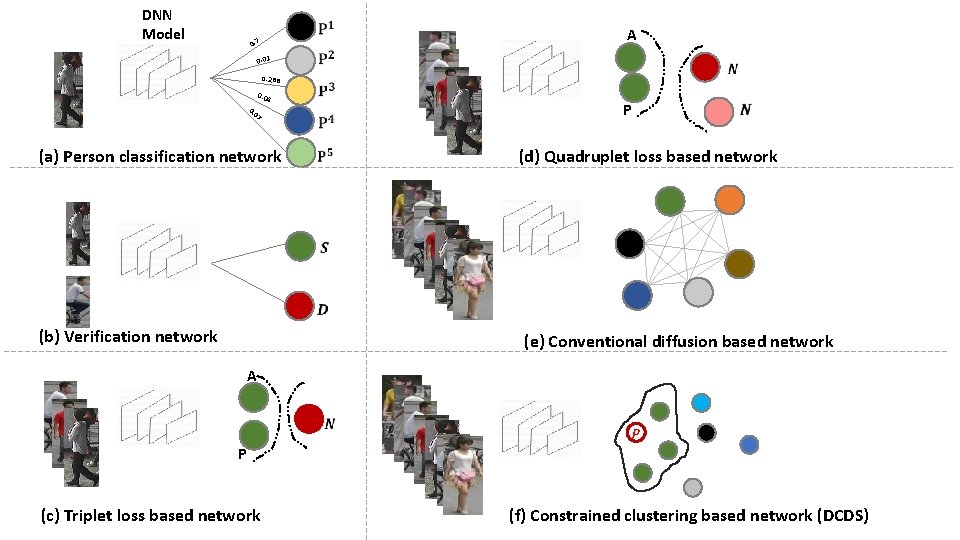
DNN Model 0. 7 0. 01 0. 288 0. 04 7 0 0. (a) Person classification network A P (d) Quadruplet loss based network (b) Verification network (e) Conventional diffusion based network A P P (c) Triplet loss based network (f) Constrained clustering based network (DCDS)

DCDS Based Network Query (Constraint)

Diffusion Based Network

DCDS Based Network 0. 10 0. 06 0. 11 0. 106 0. 01 0. 18 0. 004 0. 10 0. 121 0. 007 0. 05 0. 006 0. 12 0. 008

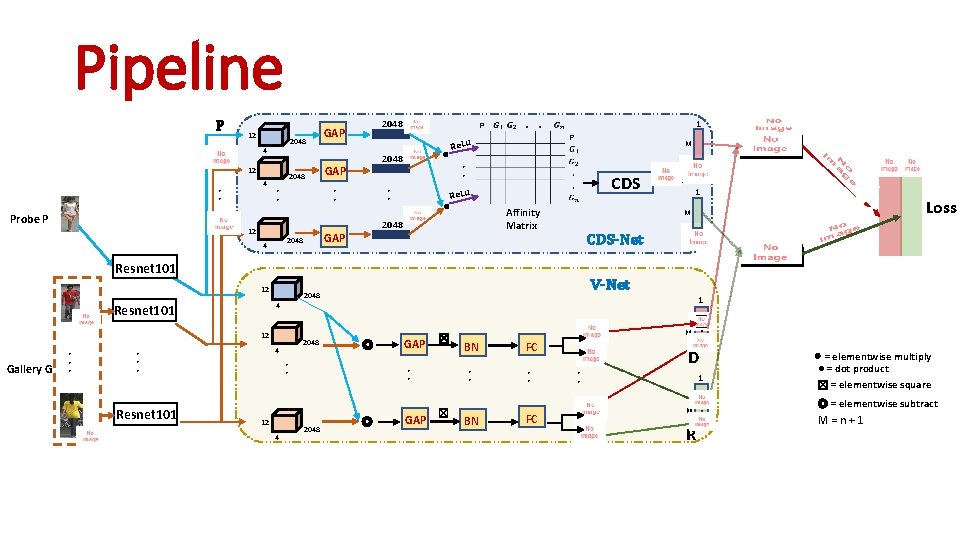
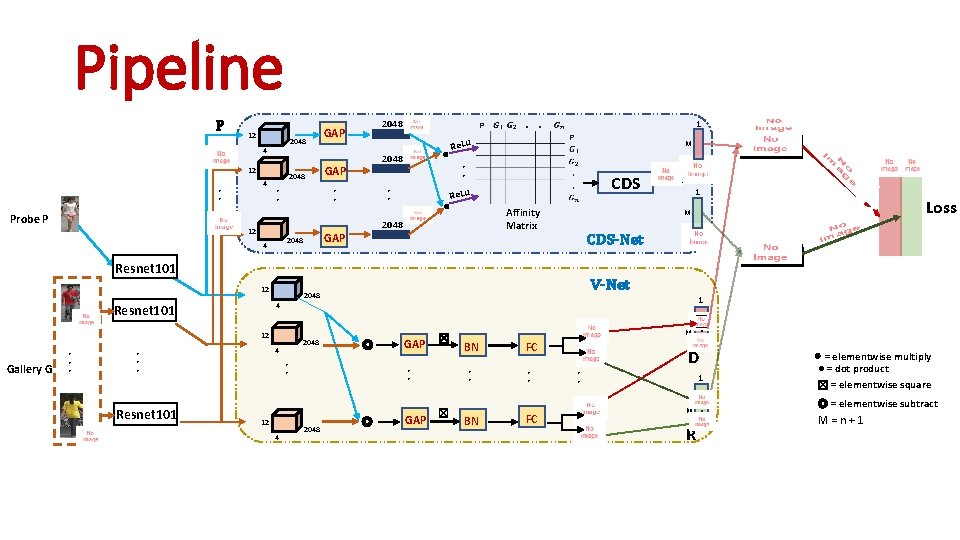
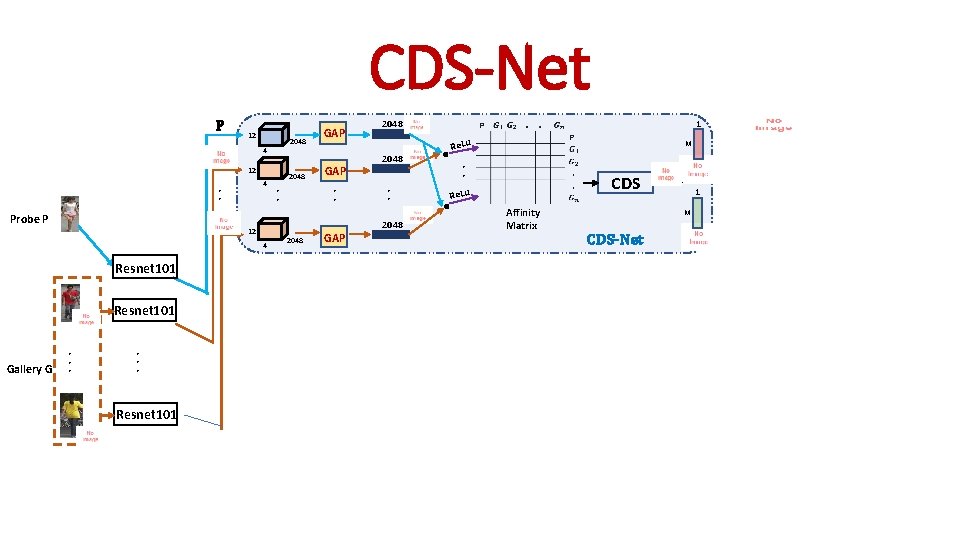
Pipeline P 12 4 • • Probe P 2048 GAP 2048 . . 1 Re. Lu M • • CDS Re. Lu • • GAP 2048 4 2048 • • 12 2048 GAP Affinity Matrix 1 CDS-Net Gallery G 4 • • • Resnet 101 2048 1 ◎ • • 12 4 GAP ☒ • • 2048 V-Net 2048 12 Loss M 4 Resnet 101 12 ◎ GAP ☒ BN FC • • BN FC . D M • • 1 . R M ⊗ = elementwise multiply ● = dot product ☒ = elementwise square ◎ = elementwise subtract M = n + 1

Pipeline P 12 4 • • Probe P 2048 GAP 2048 . . 1 Re. Lu M • • CDS Re. Lu • • GAP 2048 4 2048 • • 12 2048 GAP Affinity Matrix 1 M CDS-Net Resnet 101 12 Gallery G 12 Resnet 101 2048 4 • • • V-Net 2048 1 4 Resnet 101 ◎ • • 12 4 GAP ☒ • • 2048 ◎ GAP ☒ BN FC • • BN FC . D M • • 1 . R M ⊗ = elementwise multiply ● = dot product ☒ = elementwise square ◎ = elementwise subtract M = n + 1

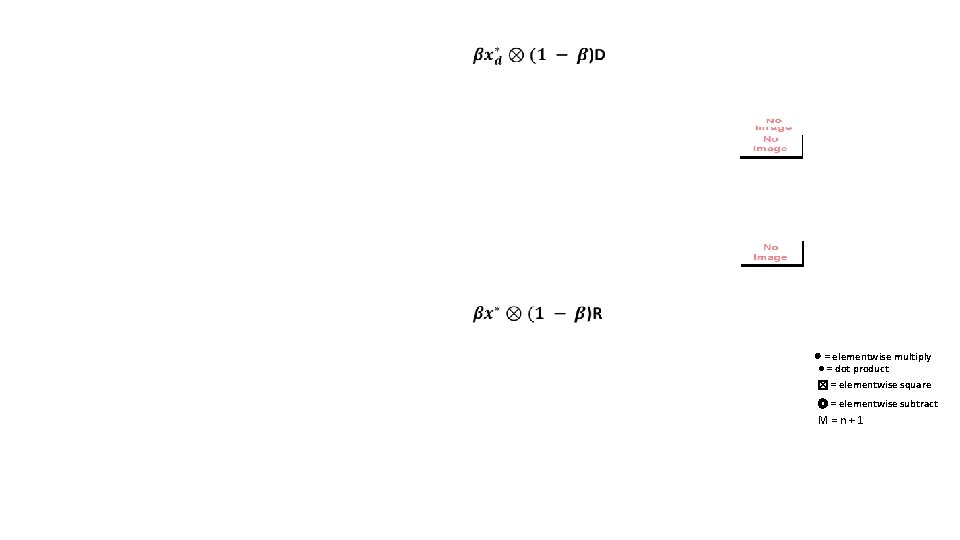
⊗ = elementwise multiply ● = dot product ☒ = elementwise square ◎ = elementwise subtract M = n + 1

Pipeline P 12 4 • • Probe P 2048 GAP 2048 . . 1 Re. Lu M • • CDS Re. Lu • • GAP 2048 4 2048 • • 12 2048 GAP Affinity Matrix 1 CDS-Net Gallery G 4 • • • Resnet 101 2048 1 ◎ • • 12 4 GAP ☒ • • 2048 V-Net 2048 12 Loss M 4 Resnet 101 12 ◎ GAP ☒ BN FC • • BN FC . D M • • 1 . R M ⊗ = elementwise multiply ● = dot product ☒ = elementwise square ◎ = elementwise subtract M = n + 1

CDS-Net P 12 4 • • Probe P 12 4 Resnet 101 Gallery G Resnet 101 • • • Resnet 101 2048 GAP • • 2048 GAP 2048 Re. Lu M • • CDS Re. Lu • • 2048 . . 1 Affinity Matrix 1 M CDS-Net

CDS-Net 1 M CDS Affinity Matrix 1 M CDS-Net

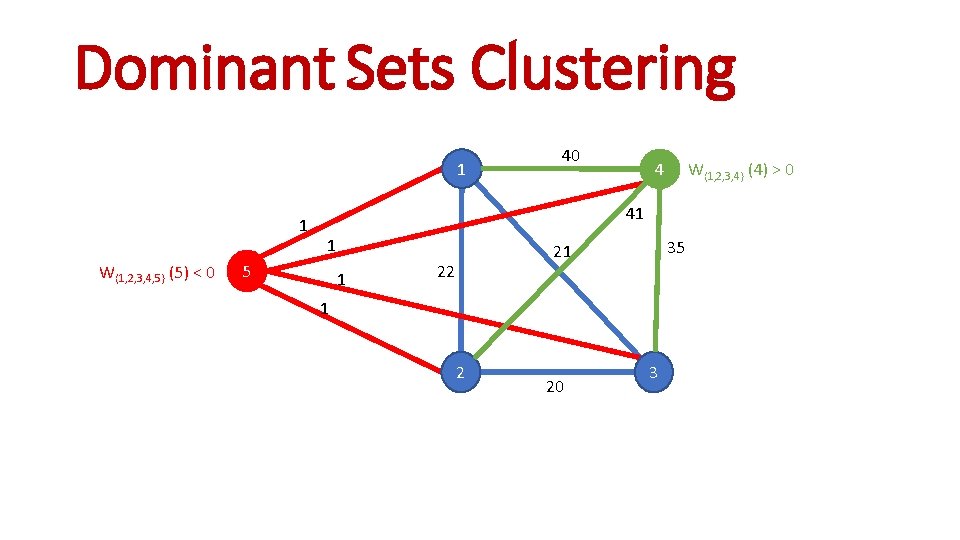
Dominant Sets Clustering • Dominant set is an edge-weighted generalization of a maximal clique Pavan et al. 2007

Dominant Sets Clustering 1 1 W{1, 2, 3, 4, 5} (5) < 0 40 4 W{1, 2, 3, 4} (4) > 0 41 1 5 1 35 21 22 1 2 20 3

Dominant Sets Clustering Consider the following linearly-constrained quadratic optimization problem [*] Pavan, M. , Pelillo, M. : Dominant sets and pairwise clustering. IEEE Trans. Pattern Anal. Mach. Intell. 29(1) (2007) 167– 172

Constrained Dominant Sets (CDS) (1)

Constrained Dominant Sets (CDS) Approaches to solve program (1): • Replicator Dynamics :

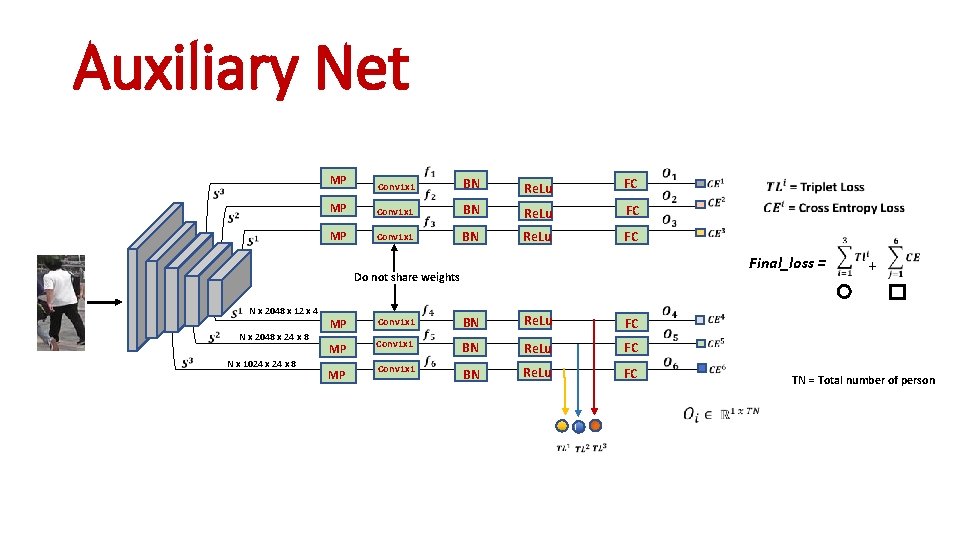
Auxiliary Net MP MP Conv 1 x 1 BN Re. Lu FC Final_loss = Do not share weights N x 2048 x 12 x 4 N x 2048 x 24 x 8 N x 1024 x 8 MP MP MP Conv 1 x 1 BN Re. Lu FC + TN = Total number of person

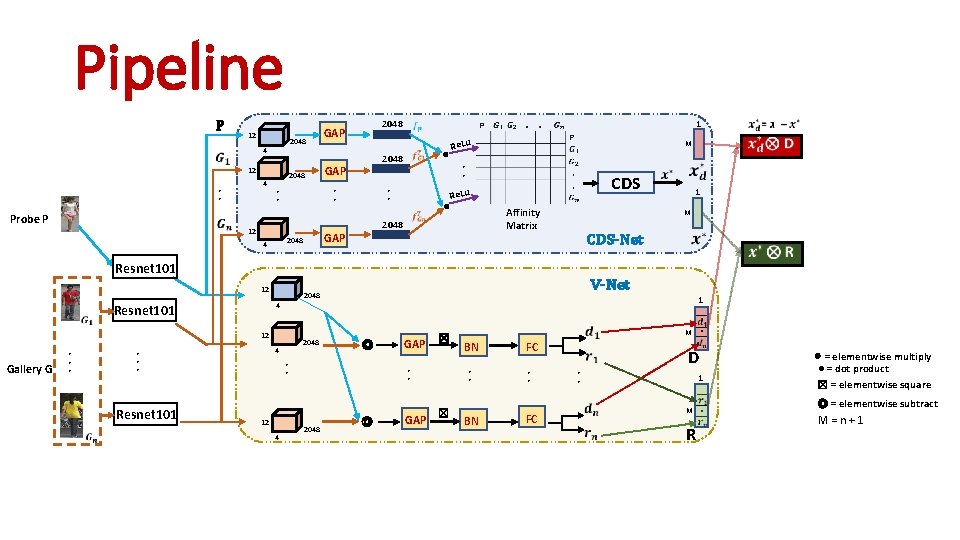
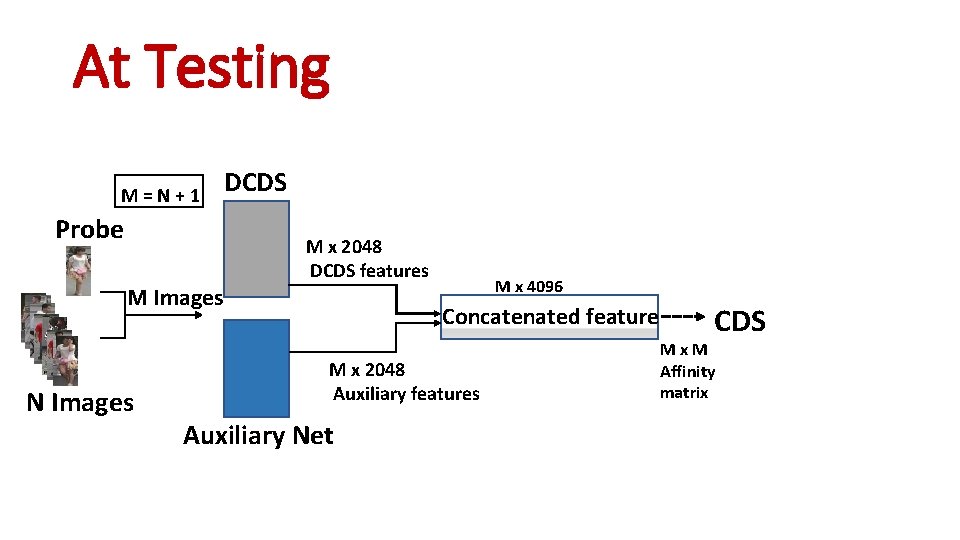
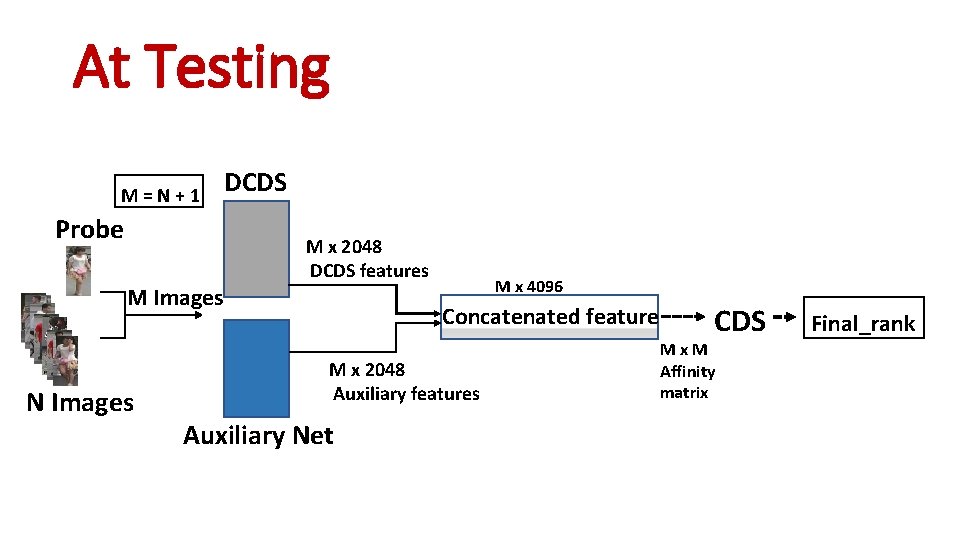
At Testing M = N + 1 Probe M Images N Images DCDS M x 2048 DCDS features M x 4096 Concatenated feature M x 2048 Auxiliary features Auxiliary Net CDS M x M Affinity matrix

At Testing CDS

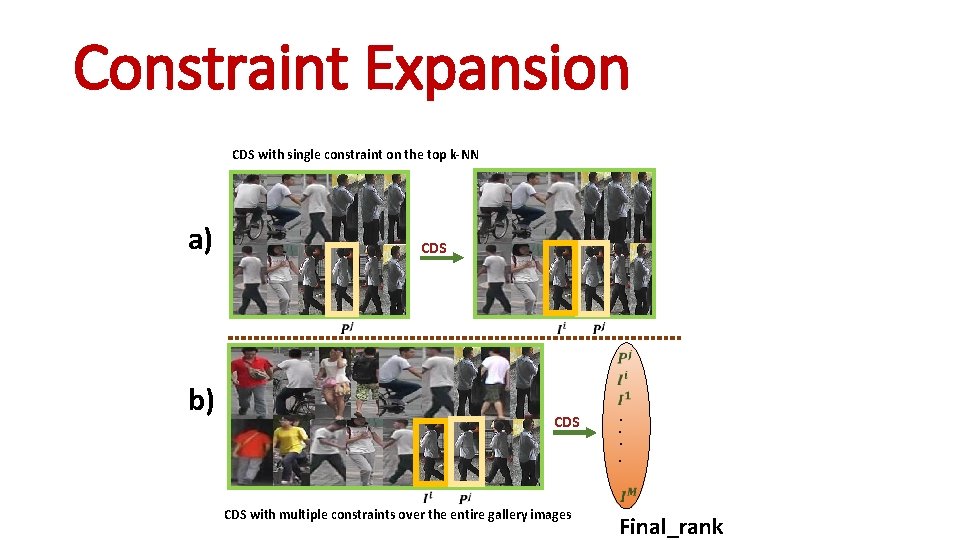
Constraint Expansion CDS with single constraint on the top k-NN a) CDS b) CDS with multiple constraints over the entire gallery images . . Final_rank

At Testing M = N + 1 Probe M Images N Images DCDS M x 2048 DCDS features M x 4096 Concatenated feature M x 2048 Auxiliary features Auxiliary Net CDS M x M Affinity matrix Final_rank

Experiments

Datasets • CUHK 03 ØTwo disjoint cameras on campus Ø 14, 097 Images of 1, 467 persons • Market 1501 ØSix cameras Ø 32, 668 images of 1501 persons • Duke. MTMC-Re-Id ØEight cameras Metrics Mean Average Precision (MAP) & Cumulated Matching Characteristics (rank-k) curves

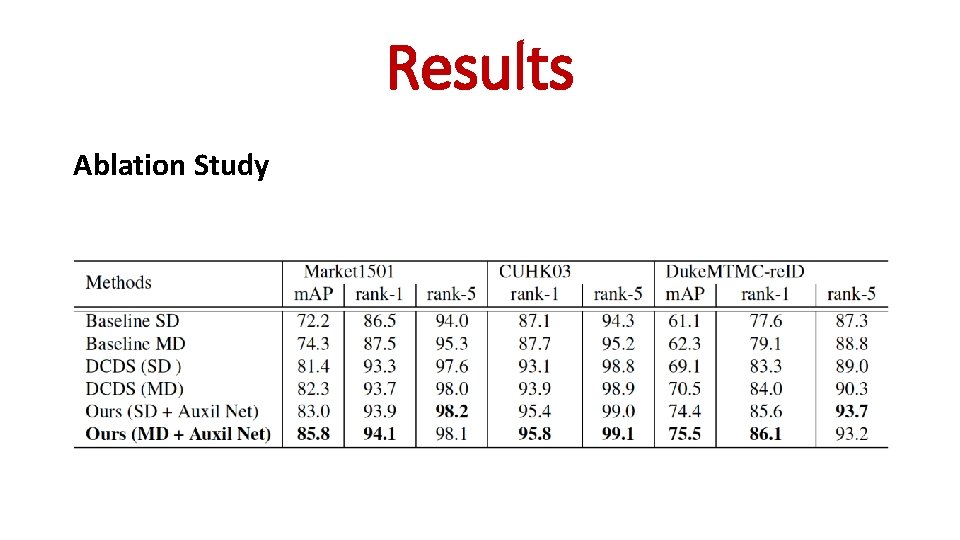
Ablation Study Results

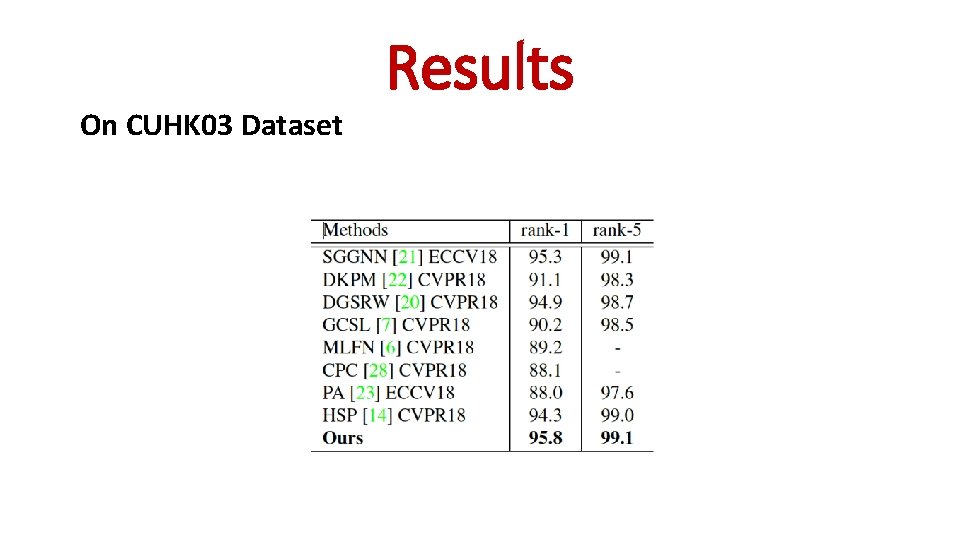
On CUHK 03 Dataset Results

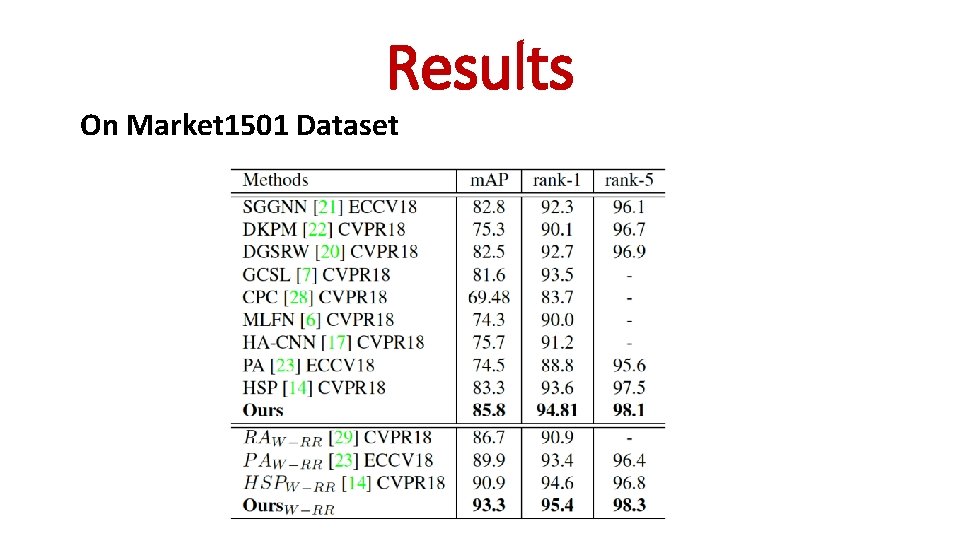
Results On Market 1501 Dataset

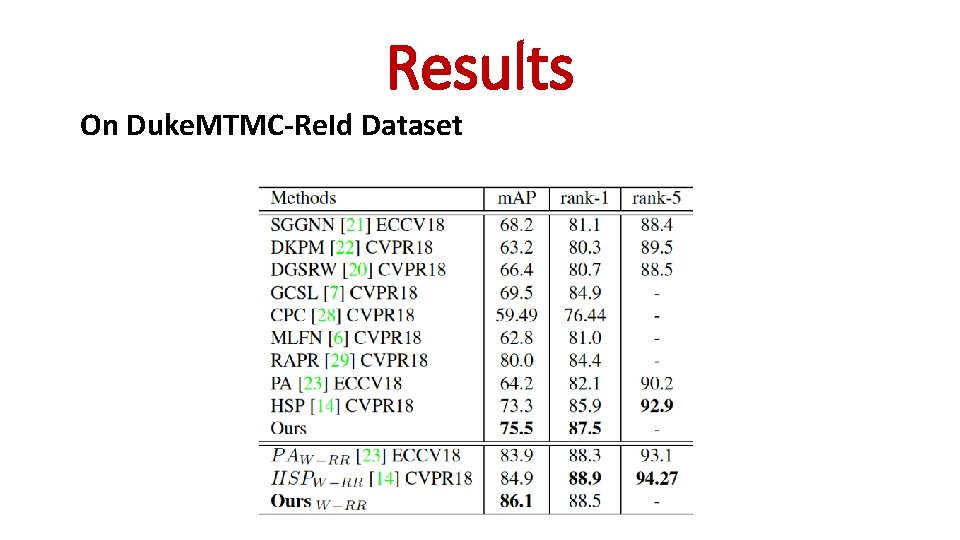
Results On Duke. MTMC-Re. Id Dataset

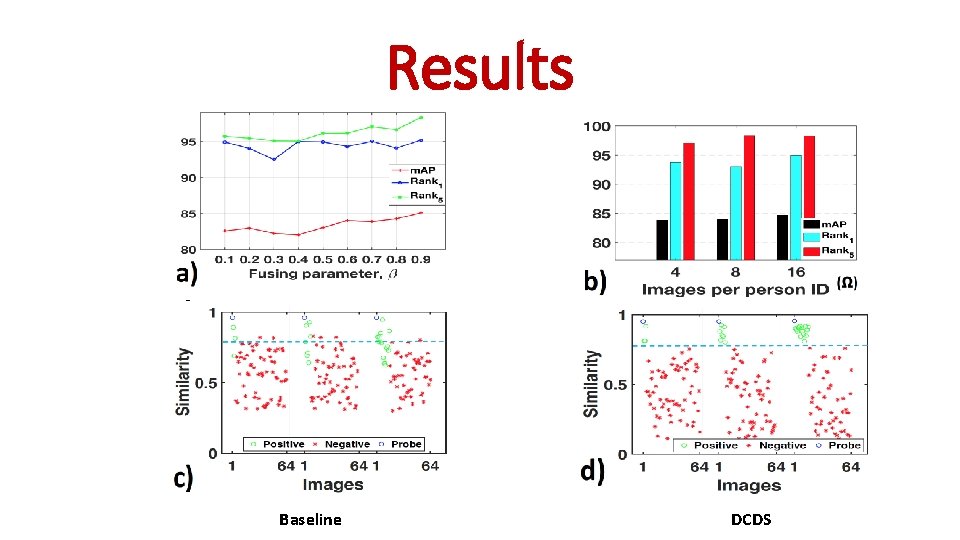
Results Baseline DCDS

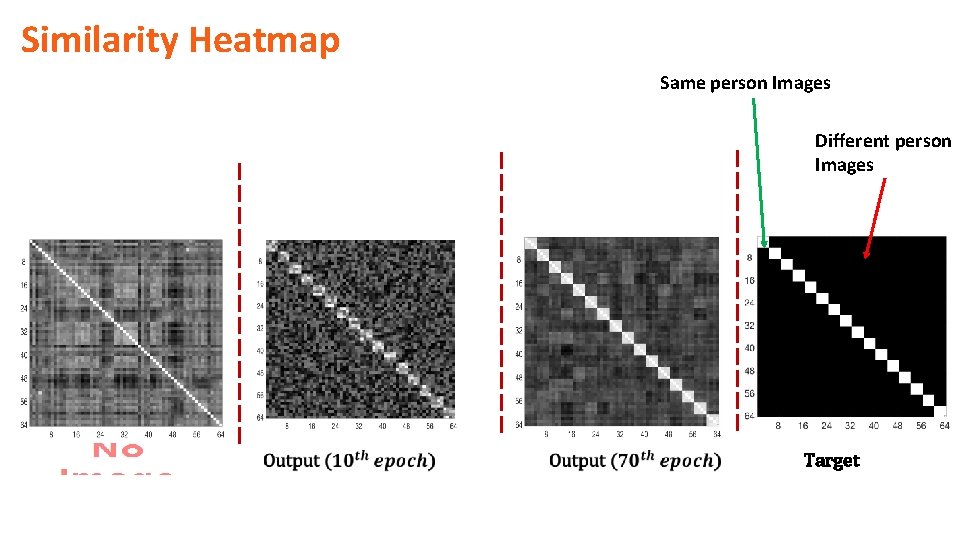
Similarity Heatmap Same person Images Different person Images Target

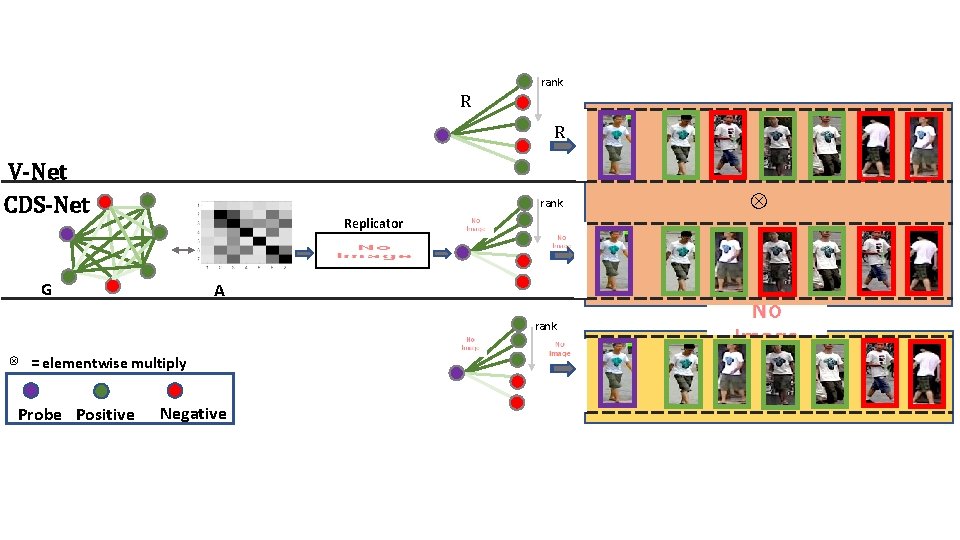
rank R R V-Net CDS-Net Replicator G ⊗ A = elementwise multiply Probe Positive ⊗ rank Negative rank

Summary • For the very first time, the dominant sets clustering method is integrated in a DNN and optimized in end-to-end fashion. • A one-to-one correspondence between person reidentification and constrained clustering problem is established. • State-of-the-art results are significantly improved. • As a future work, we would like to investigate dominant sets clustering as a loss function.

Thank you