Deep Bed Drying Calculations n In deep bed

Deep Bed Drying (Calculations)

n In deep bed drying, • All the samples in the dryer are not fully exposed to the same condition of drying air Condition of dry air at any point in mass, changes with time and with the depth of sample bed Drying in the deep bed can be taken as a sum of several thin layers Humidity and temperature of air entering and leaving each layer vary with time depending upon the stage of drying, the moisture removing from the dry layer until equilibrium moisture content is reached • • •

Some examples for deep bed drying n n Drying grain (e. g. , shelled corn) with the drying air flowing through more than two to three layers of kernels Dehydration of solid food materials
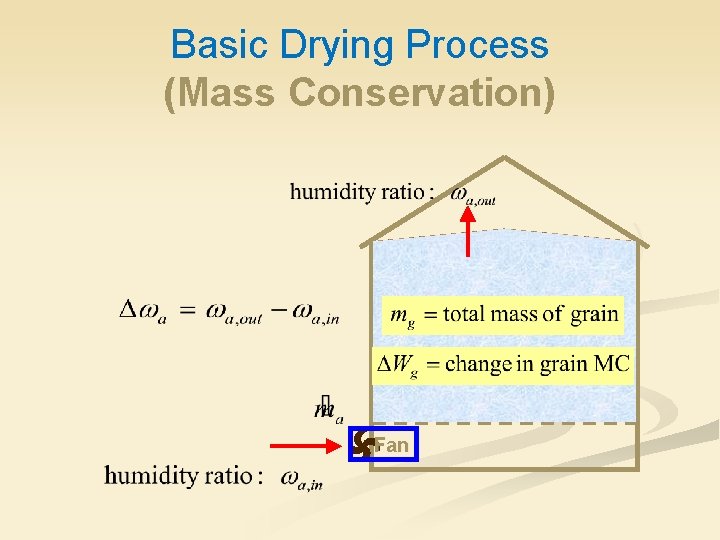
Basic Drying Process (Mass Conservation) Fan

n Total moisture conservation equation compare: moisture added to air to moisture removed from product kga kgw s s kga n Drying time kgg kgw kgg

Heat balance for drying n n n n n Q- Air flow rate m 3/min v – specific volume m 3/kg (dry air) Ca – specific heat of air k. J/kg Ta- Temperature of air in plenum 0 C Tg- Temperature of air leaving grain mass 0 C hfg –Latent heat of vaporization k. J/kg moisture DM – Dry matter content kg M 0 – Initial Moisture content (db - decimal) Me – Final equilibrium moisture content (db-decimal)

n Time taken by the drying front to reach the top of the bed can be calculated using following equation Where, M 0 = % Dry basis initial moisture content of the sample Mav = % Dry basis average moisture content at the end of the drying front advance to the top t = Time of advance (hr) A = Cross sectional area of the dryer through which air passes m = Mass flow rate of dry air (kg/ hr. m 2) Ф 2= Humidity of air leaving the dryer Ф 1 = Humidity of air entering the dryer DM = Mass of the dry sample in the bin (kg)

For the changes in drying air conditions psychrometric principles can be applied Example Hard wheat at 75°F is being dried from 18% to 12% w. b. in a batch grain drier. Drying will be stopped when the top layer reaches 13%. Ambient conditions: Tdb = 70°F, RH = 20% n Determine the exit air temperature early in the drying period? n Determine the exit air RH and
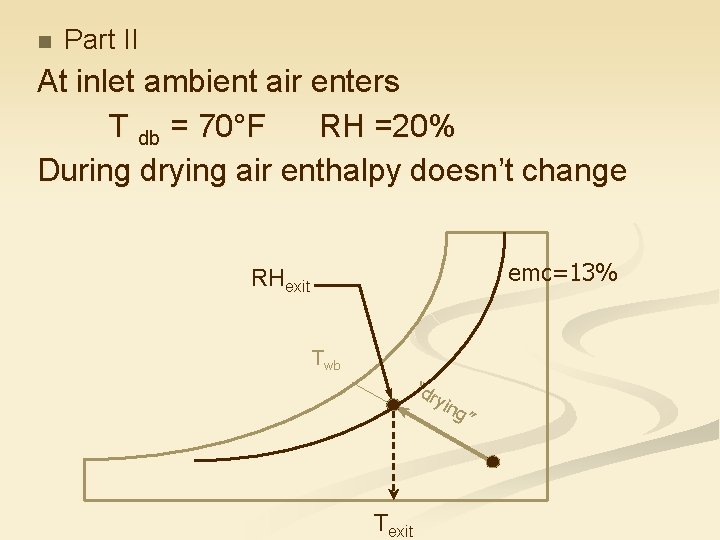
n Part II At inlet ambient air enters T db = 70°F RH =20% During drying air enthalpy doesn’t change emc=13% RHexit Twb “dr yin Texit g”
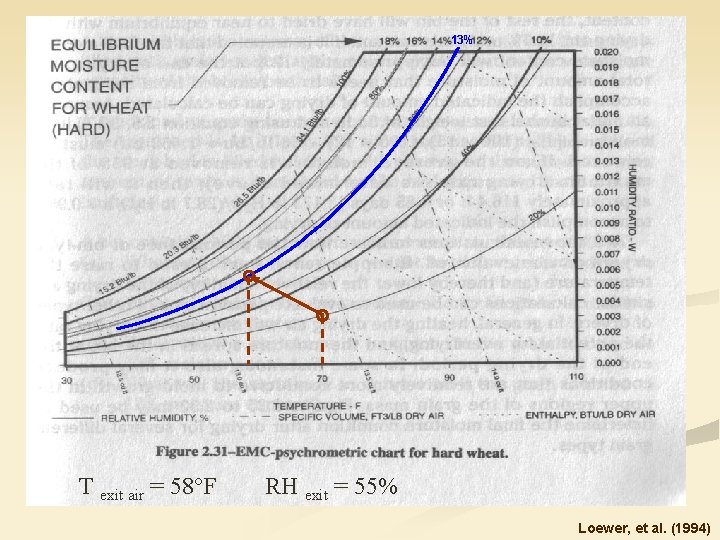
13% T exit air = 58°F RH exit = 55% Loewer, et al. (1994)
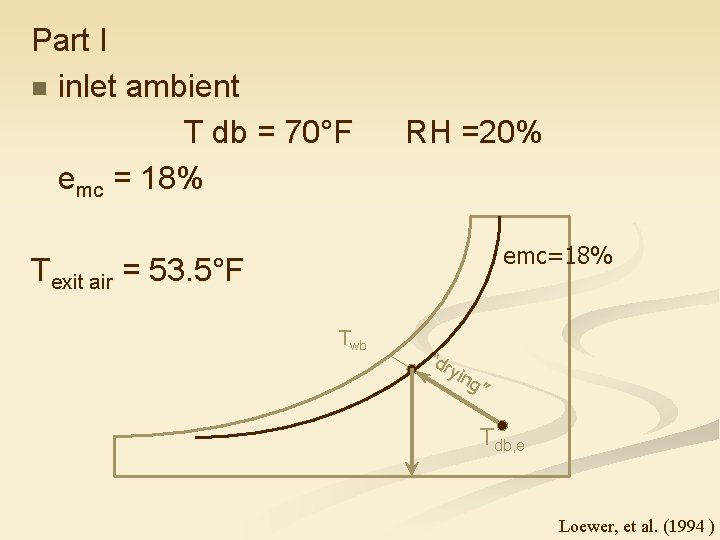
Part I n inlet ambient T db = 70°F emc = 18% RH =20% emc=18% Texit air = 53. 5°F Twb “dr yin g” Tdb, e Loewer, et al. (1994 )

Mathematical models for Deep- bed drying process

n n Mathematical models are needed to predict temperature and moisture profiles in the deep-bed and inside the grain The models propose that the system with two control volumes Grain where moisture is at liquid phase n Humid air outside the kernel n n n To pull the moisture from grain and to enter to the vapor phase sensible and latent heat is needed Models assume the steady state drying

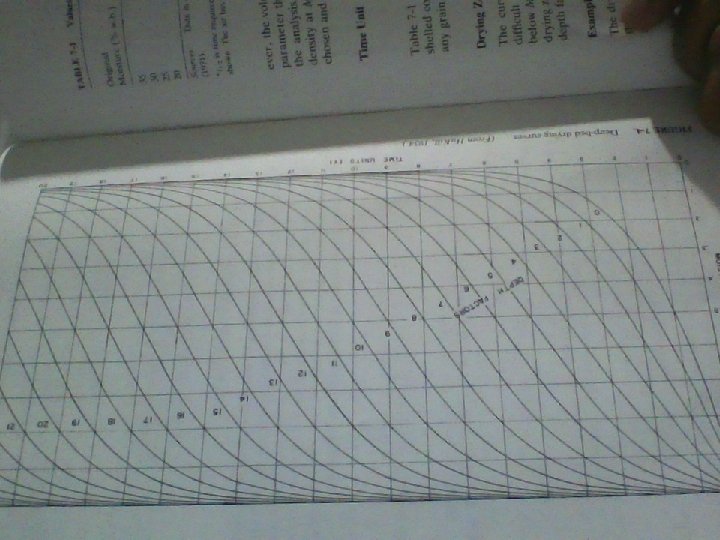
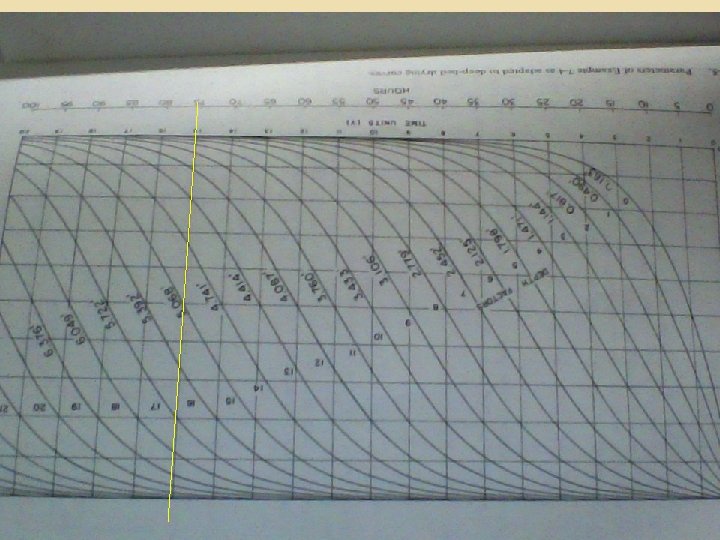
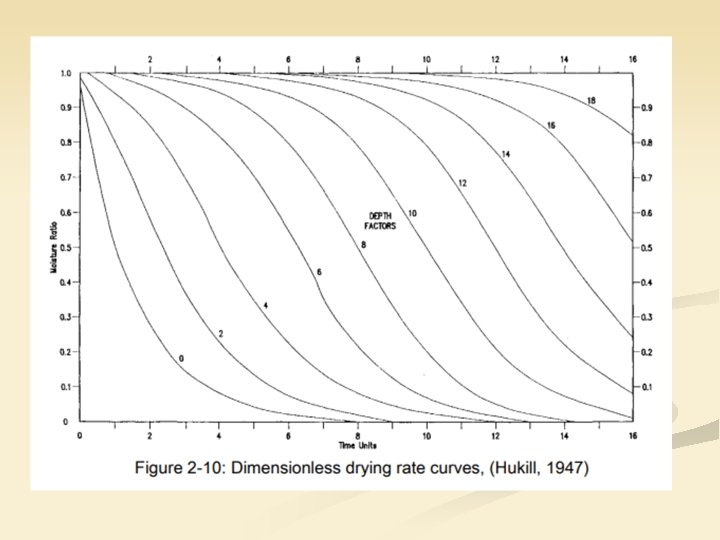
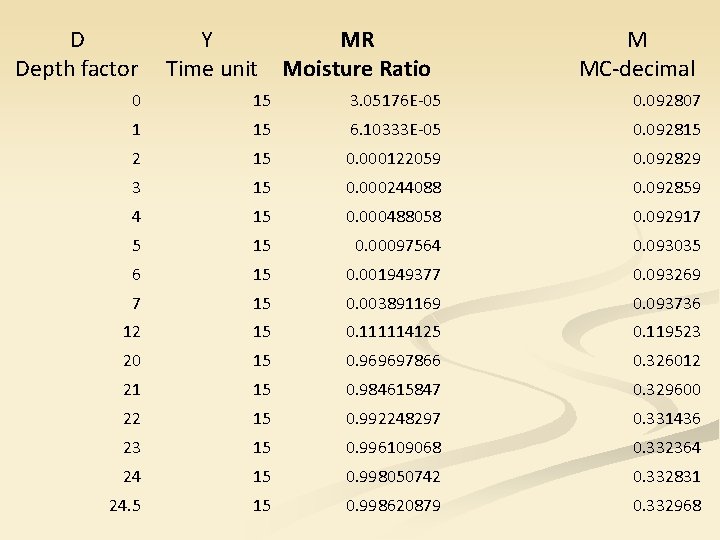
n n n According to Hukill ( 1947, 1954) bulk drying curves can be used to find: approximate moisture content at any depth in the deep bed drying system at any time after drying has started Three parameters were used to represent any deep drying systems n Moisture ratio ( MR) n Depth factor ( D) n Time unit ( Y)

Moisture ratio Where, MR = ( M – Me ) / ( Mo - Me ) Mo = Moisture content at the start of drying ( d. b. , decimal ) M = Grain Moisture ( d. b. , decimal ) Me = Moisture content when the grain as reached equilibrium with air D = Depth factor Y = Time unit

Depth factor (D) n DM’ is needed to calculate depth factor DM’ is constant throughout the drying period DM’ = dry matter per depth factor Tg = Temperature of exit air Ta = Temperature of inlet air hfg = Btu/ lb cfm = Air flow rate in cubic ft per minute ca = Btu/lb v = ft 3 / lb

Depth factor zero (D=0) n n However, D=0 contains half of the grains of the other depth factors DM’ – is considered as a constant value throughout the drying period (volume of grain/depth factor depends on density, it changes with drying ? ? But to simplify the analysis assume no shrinkage. Select a logical value, ie at M 0 )

Time unit ( Y) Y = t / t 1/2 = Time required for fully exposed grain to dry from MR=1 to MR = 0. 5 ( obtained from a table ) t = Drying time
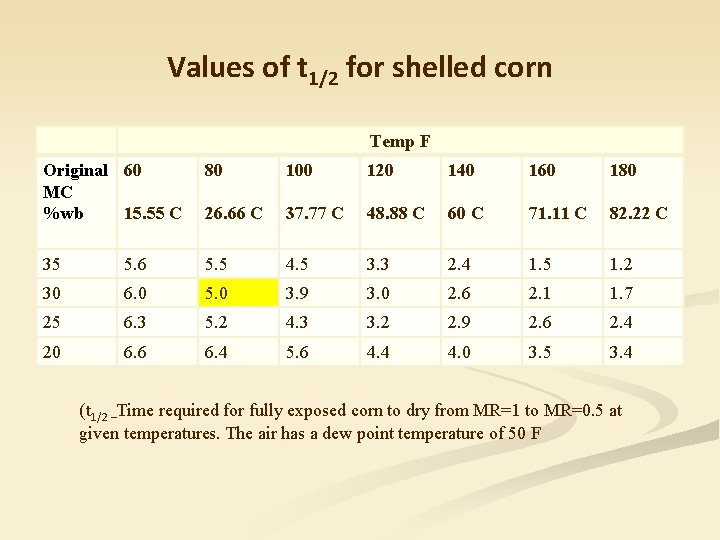
Values of t 1/2 for shelled corn Temp F Original 60 MC %wb 15. 55 C 80 100 120 140 160 180 26. 66 C 37. 77 C 48. 88 C 60 C 71. 11 C 82. 22 C 35 5. 6 5. 5 4. 5 3. 3 2. 4 1. 5 1. 2 30 6. 0 5. 0 3. 9 3. 0 2. 6 2. 1 1. 7 25 6. 3 5. 2 4. 3 3. 2 2. 9 2. 6 2. 4 20 6. 6 6. 4 5. 6 4. 4 4. 0 3. 5 3. 4 (t 1/2 –Time required for fully exposed corn to dry from MR=1 to MR=0. 5 at given temperatures. The air has a dew point temperature of 50 F

Example Air flow rate in a dryer = 16330 cfm Ta = 83. 5 F -Air temp at the plenum Фa = 35% (RH) Tg = 64. 0 F-exit air temp, Ca- 0. 24 BTU/lb F v = 13. 86 ft 3/lb specific volume of air M 0 = 33. 33% db Me = 9. 28% db -at plenum air conditions Dia of the dryer -27 ft-Floor area = 573 ft 2 - height of grain 8 ft Given Drying time 75 h Find a). Location of the drying zone b). The thickness of the zone c). The average moisture content of the grain 1.

n n n n n T 1/2 = 5 h MR= M - Me / (M 0 - Me ) M = Me + MR (M 0 - Me) MR M 0 9. 28 0. 1 11. 69 0. 2 14. 09. . 1. 0 33. 33

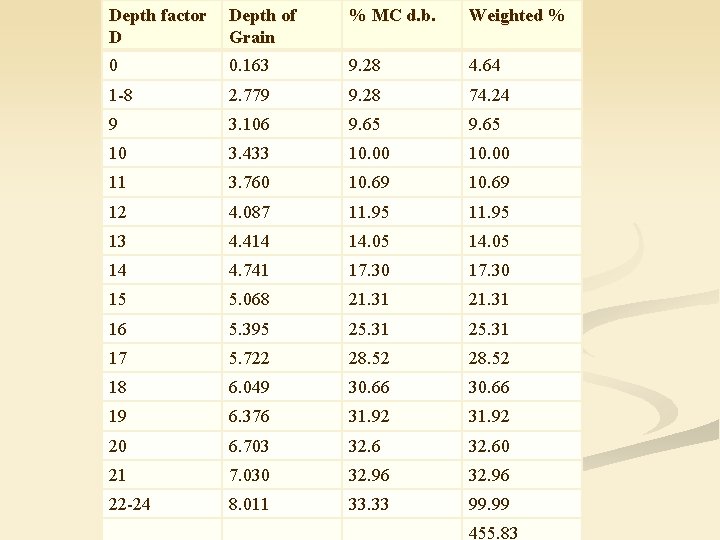
n n n Y = t/ t 1/2 t=Y*5 Y = 75/5 = 15 Refer to the drying curves pgs 197 -98 a) after 75 h drying, bottom of the drying zone is 8. 5 depth factors (or 2. 78 ft) from the bottom Top of the zone is 21. 5 depth factors (or 7. 03 ft) from the bottom To calculate the height of a depth factor Use the DM’ equation b) Drying zone = 7. 03 - 2. 78 ft

n DM’ – Dry matter per depth factor = 5732 lb dry matter per depth factor Grain density at M 0 (25% (w. b. ) = 40. 8 lb/ft 3 Dry mass per 1 ft 3 = 40. 8 * 0. 75 lb Volume per Depth factor = 5732/40. 8*0. 75 = 187. 32 ft 3 Floor area of the dryer = 573 ft 2 - Given

The thickness of a depth factor = Vol of a depth factor/floor area of the dryer = 187. 32 ft 3 / 573 ft 2 = 0. 327 ft But “ 0” DF = ½ * 0. 327 = 0. 163 ft Mc (d. b. ) can be read from the graph Mc along the 15 Y line for curves or can be calculated from MR=(M-Me)/(Min – Me) M av = weighted %/total No of Depth factors = 455. 83%/24. 5 = 18. 61 d. b. Or 15. 69 w. b.
D Depth factor Y Time unit MR Moisture Ratio M MC-decimal 0 15 3. 05176 E-05 0. 092807 1 15 6. 10333 E-05 0. 092815 2 15 0. 000122059 0. 092829 3 15 0. 000244088 0. 092859 4 15 0. 000488058 0. 092917 5 15 0. 00097564 0. 093035 6 15 0. 001949377 0. 093269 7 15 0. 003891169 0. 093736 12 15 0. 111114125 0. 119523 20 15 0. 969697866 0. 326012 21 15 0. 984615847 0. 329600 22 15 0. 992248297 0. 331436 23 15 0. 996109068 0. 332364 24 15 0. 998050742 0. 332831 24. 5 15 0. 998620879 0. 332968
Depth factor D Depth of Grain % MC d. b. Weighted % 0 0. 163 9. 28 4. 64 1 -8 2. 779 9. 28 74. 24 9 3. 106 9. 65 10 3. 433 10. 00 11 3. 760 10. 69 12 4. 087 11. 95 13 4. 414 14. 05 14 4. 741 17. 30 15 5. 068 21. 31 16 5. 395 25. 31 17 5. 722 28. 52 18 6. 049 30. 66 19 6. 376 31. 92 20 6. 703 32. 60 21 7. 030 32. 96 22 -24 8. 011 33. 33 99. 99 455. 83

End

A simple model for drying rice grains in a deep bed dryer n n The deep bed drying can be described as several thin layers If height of the bed is Z, air entering at Z=0 and air leaving from the bed at Z=L Uniform temperature distribution across the grain phase is assumed. But the temperature is changed. Drying process inside the grain requires a two phase model. At the second falling rate

Xms= Maximum sorption water content X 0 = Initial moisture content Xeq = Equilibrium moisture content D 0 = Diffusion coefficient at initial time(m 2 s-1) Equilibrium moisture content is calculated using isotherm

D 0 = Diffusion coefficient at initial time D 1 = Constant of Arrhenius type equation (m 2 s-1) Ea = Activation energy per unit mass (Jkg-1) R = Ideal gas constant ( Jkg-1 k-1) T = Time (s)

Conservation of mass equation state the moisture loss by the grain phase X = Grain moisture content ( kg moisture / kg drain ) Wa = Axial drying air flux per unit of deep bed cross sectional area ( m s-1) H = Absolute air humidity ( kg moisture/kg dry air)

Energy conservation for each of the thin layer n Heated air can evaporate water coming from the grain and increase the temperature from Ts to Tg Energy balance,

Change of rice temperature in solid and liquid phase cpv = Specific heat of vapor (Jkg-1 k-1) Cpw = Specific heat of water ( Jkg-1 k-1) haeff = Volumetric pseudo convective heat transfer coefficient (Wm-3 k-1)

Tg = Air temperature Ts = Temperature of solid ρss = Apparent density of dry grain ρa = Density of dry air lv = Vaporization heat of water ( Jkg-1)

Modeling of temperature changes in air phase

Thank You
- Slides: 39