DEDUCTIVE REASONING We reason deductively when we draw

DEDUCTIVE REASONING We reason deductively when we draw a conclusion from a set of given facts using the laws of logic

Inspector Garble

DEDUCTIVE REASONING • If the butler murdered Uncle Alfred then there are fingerprints on the gun. • The butler murdered Uncle Alfred or the maid did it. • There are not fingerprints on the gun. • Therefore the maid did it.

The collection of statements below is called an ARGUMENT a vehicle for reasoning consisting of A set of statements called PREMISES - the given facts or clues Followed by a final statement called the CONCLUSION which is said to be drawn from the given facts. • If the butler murdered Uncle Alfred then there are fingerprints on the gun. • The butler murdered Uncle Alfred or the maid did it. • There are not fingerprints on the gun. • Therefore the maid did it.

An argument is either VALID or INVALID does NOT mean TRUE The sky is blue. Zebras have stripes. We are sitting in class. Therefore George W. Bush is president of the United States. Everything I say is true but the process of reasoning is not valid. The premises and the conclusion are not related. To examine the relationship that determines validity, we must first consider the STRUCTURE of the argument.

WHODUNNIT? • If the butler murdered Uncle Alfred then there are fingerprints on the gun. • The butler murdered Uncle Alfred or the maid did it. • There are not fingerprints on the gun. • Therefore the maid did it.

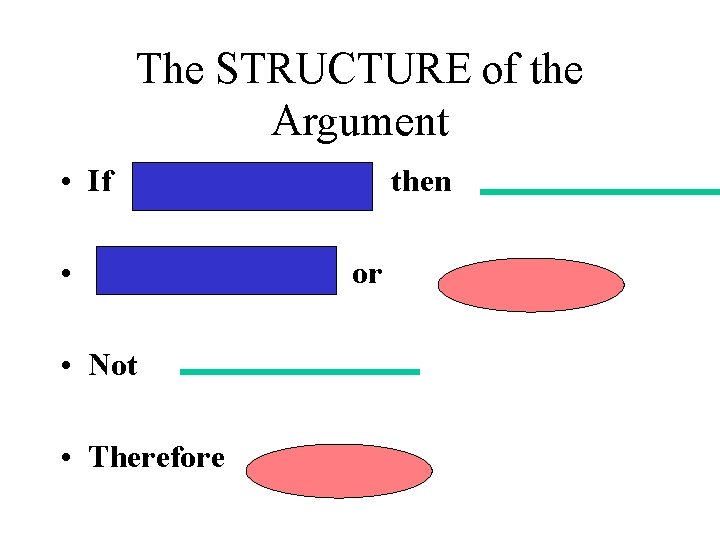
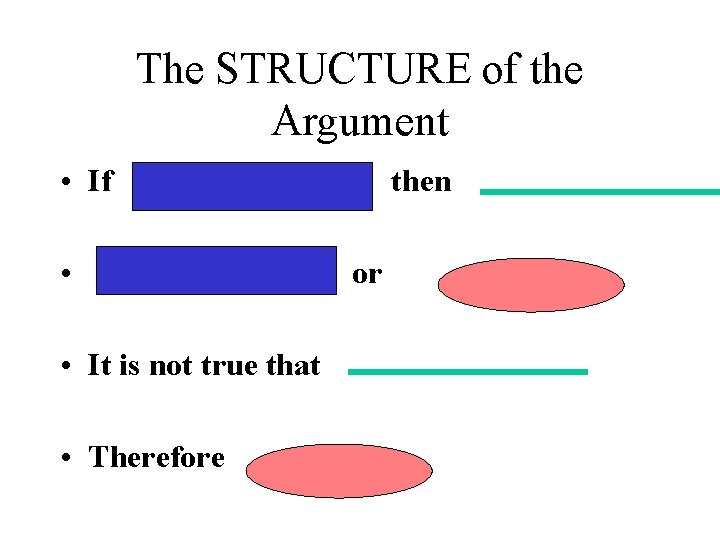
The STRUCTURE of the Argument • If • • Not • Therefore then or

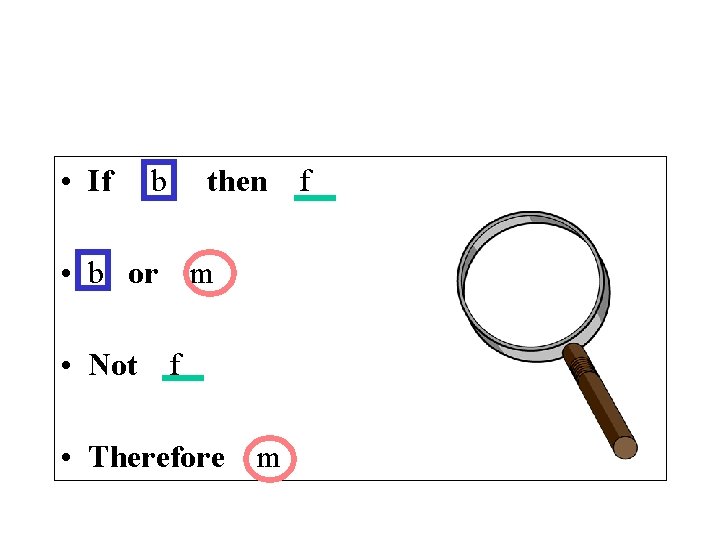
• If b then • b or m • Not f • Therefore m f

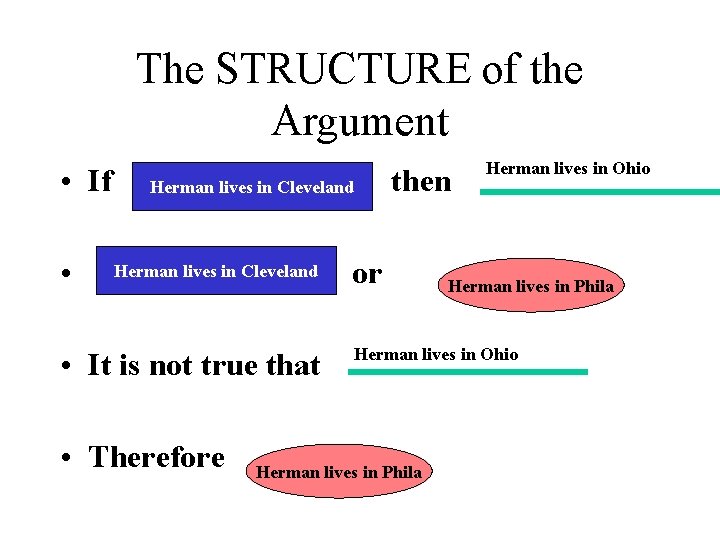
This argument has the same structure as the previous example • If Herman lives in Cleveland then Herman lives in Ohio. • Herman lives in Cleveland or Herman lives in Philadelphia. • Herman does not live in Ohio. • Therefore Herman lives in Philadelphia.

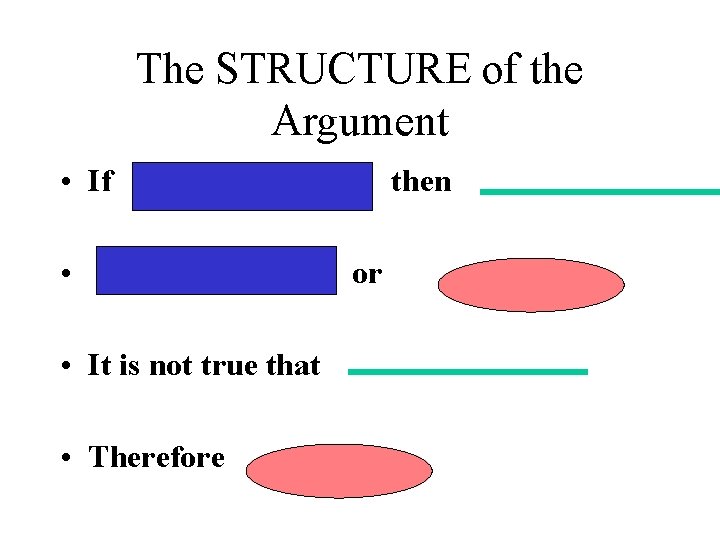
The STRUCTURE of the Argument • If • • It is not true that • Therefore then or

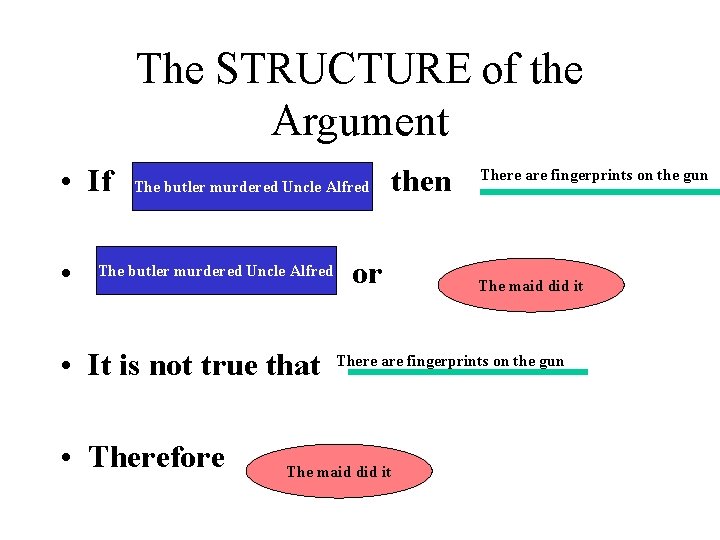
The STRUCTURE of the Argument • If • The butler murdered Uncle Alfred • It is not true that • Therefore then or There are fingerprints on the gun The maid did it

The STRUCTURE of the Argument • If • • It is not true that • Therefore then or

The STRUCTURE of the Argument • If • then Herman lives in Cleveland • It is not true that • Therefore or Herman lives in Ohio Herman lives in Phila

When we reason inductively we can never be certain that the conclusion is true. When we reason deductively we can be certain that the conclusion is true as long as the premises are true. It is difficult to separate these two modes of reasoning, because we often use them together - for example, in deductive reasoning, the premises are likely to be the conclusions of inductive reasoning. Inductive reasoning is uncertain - but it is our only way to know anything about the real world. Deductive reasoning is certain - but very artificial. However these artificial patterns govern the way we think, reason and communicate.

Albert Einstein compares the two modes of reasoning inductive and deductive - and outlines the great paradox in our ability to “know” things: Logical reasoning “As far as mathematics is certain, it does not pertain to reality, and as far as it pertains to reality, it is not certain. ”