Deductive Databases Outline Chapter 25 3 rd ed

Deductive Databases Outline Chapter 25 – 3 rd ed. (Chap. 24. 4 – 4 th, 5 th ed. ; 26. 5, 6 th ed. ) • What is a deductive database system? • Some basic concepts • Basic inference mechanism for logic programs • Datalog programs and their evaluation Jan. 2012 Yangjun Chen ACS-3902 1

Deductive Databases • What is a deductive database system? A deductive database can be defined as an advanced database augmented with an inference system. Database + Deductive database Inference By evaluating rules against facts, new facts can be derived, which in turn can be used to answer queries. It makes a database system more powerful. Jan. 2012 Yangjun Chen ACS-3902 2

Deductive Databases • Some basic concepts from logic To understand the deductive database system well, some basic concepts from mathematical logic are needed. - term - n-ary predicate - literal - (well-formed) formula - clause and Horn-clause - facts - logic program Jan. 2012 Yangjun Chen ACS-3902 3

Deductive Databases - term A term is a constant, a variable or an expression of the form f(t 1, t 2, . . . , tn), where t 1, t 2, . . . , tn are terms and f is a function symbol. - Example: a, b, c, f(a, b), g(a, f(a, b)), x, y, g(x, y) - n-ary predicate An n-ary predicate symbol is a symbol p appearing in an expression of the form p(t 1, t 2, . . . , tn), called an atom, where t 1, t 2, . . . , tn are terms. p(t 1, t 2, . . . , tn) can only evaluate to true or false. - Example: p(a, b), q(a, f(a, b)), p(x, y) Jan. 2012 Yangjun Chen ACS-3902 4

Deductive Databases - literal A literal is either an atom or its negation. - Example: p(a, f(a, b)), p(a, f(a, b)) - (well-formed) formula - A well-formed (logic) formula is defined inductively as follows: - An atom is a formula. - If P and Q are formulas, then so are P, (P Q), and (P Q). - If x is a variable and P is a formula containing x, then ( x. P) and ( x. P) are formulas. Jan. 2012 Yangjun Chen ACS-3902 5

Deductive Databases - clause - A clause is an expression of the following form: A 1 A 2 . . . An B 1 . . . Bm where Ai and Bj are atoms. - The above expression can be written in the following equivalent form: B 1 . . . Bm A 1 . . . An consequent or antecedent B 1, . . . , Bm A 1 , . . . , An Jan. 2012 Yangjun Chen ACS-3902 6

Deductive Databases - - clause A B A B A B B A 1 0 1 0 1 1 0 1 Horn clause A Horn clause is a clause with the head containing only one positive atom. Bm A 1 , . . . , An Jan. 2012 Yangjun Chen ACS-3902 7

Deductive Databases - fact - A fact is a special Horn clause of the following form: B with all variables in B being instantiated. (B can be simply written as B. ) - logic program A logic program is a set of Horn clauses. Jan. 2012 Yangjun Chen ACS-3902 8
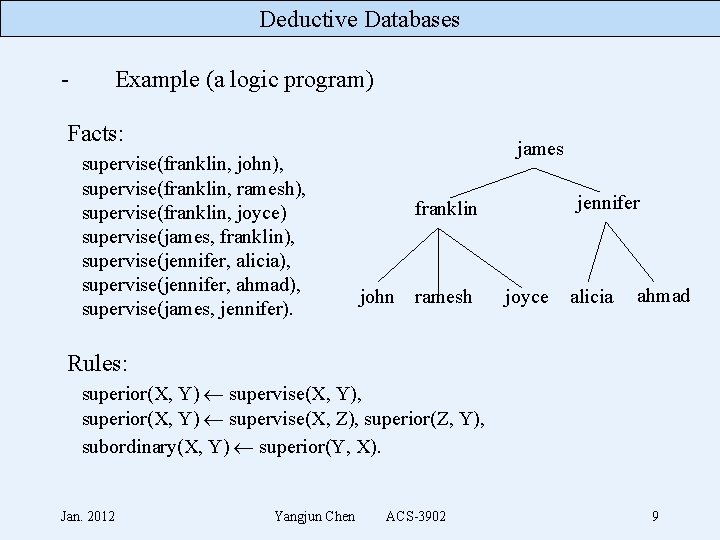
Deductive Databases - Example (a logic program) Facts: supervise(franklin, john), supervise(franklin, ramesh), supervise(franklin, joyce) supervise(james, franklin), supervise(jennifer, alicia), supervise(jennifer, ahmad), supervise(james, jennifer). james jennifer franklin john ramesh joyce alicia ahmad Rules: superior(X, Y) supervise(X, Y), superior(X, Y) supervise(X, Z), superior(Z, Y), subordinary(X, Y) superior(Y, X). Jan. 2012 Yangjun Chen ACS-3902 9

Deductive Databases Facts can be considered as the data stored as relations in a relational database. Jan. 2012 Yangjun Chen ACS-3902 10

Deductive Databases • Basic inference mechanism for logic programs - interpretation of programs (rules + facts) There are two main alternatives for interpreting theoretical meaning of rules: proof theoretic, and model theoretic interpretation - proof theoretic interpretation 1. The facts and rules are considered to be true statements, or axioms. facts - ground axioms rules - deductive axioms 2. The deductive axioms are used to construct proofs that derive new facts from existing facts. Jan. 2012 Yangjun Chen ACS-3902 11

Deductive Databases - Example: 1. 2. superior(X, Y) supervise(X, Y). superior(X, Y) supervise(X, Z), superior (Z, Y). 3. 4. supervise(jennifer, ahmad). supervise(james, jennifer). (ground axiom, given) 5. 6. superior(jennifer, ahmad). superior(james, ahmad). (apply rule 1 on 3) (apply rule 2 on 4 and 5) Jan. 2012 Yangjun Chen ACS-3902 (rule 1) (rule 2) 12

Deductive Databases - model theoretic interpretation 1. Given a finite or an infinite domain of constant values, assign to each predicate in the program every possible combination of values as arguments. 2. All the instantiated predicates contitute a Herbrand base. 3. An interpretation is a subset of the Herbrand base. 4. In the Herbrand base, each instantiated predicate evaluates to true or false in terms of the given facts and rules. 5. An interpretation is called a model for a specific set of rules and the corresponding facts if those rules are always true under that interpretation. 6. A model is a minimal model for a set of rules and facts if we cannot change any element in the model from true to false and still get a model for these rules and facts. Jan. 2012 Yangjun Chen ACS-3902 13

Deductive Databases - Example: 1. superior(X, Y) supervise(X, Y). 2. superior(X, Y) supervise(X, Z), superior(Z, Y). (rule 1) (rule 2) known facts: supervise(franklin, john), supervise(franklin, ramesh), supervise(franklin, joyce), supervise(james, franklin), supervise(jennifer, alicia), supervise(jennifer, ahmad), supervise(james, jennifer). For all other possible (X, Y) combinations supervise(X, Y) is false. domain = {james, franklin, john, ramesh, joyce, jennifer, alicia, ahmad} Jan. 2012 Yangjun Chen ACS-3902 14

Deductive Databases Interpretation - model - minimal model known facts: supervise(franklin, john), supervise(franklin, ramesh), supervise(franklin, joyce), supervise(james, franklin), supervise(jennifer, alicia), supervise(jennifer, ahmad), supervise(james, jennifer). For all other possible (X, Y) combinations supervise(X, Y) is false. derived facts: superior(franklin, john), superior(franklin, ramesh), superior(franklin, joyce), superior(jennifer, alicia), superior(jennifer, ahmad), superior(james, franklin), superior(james, jennifer), superior(james, john), superior(james, ramesh), superior(james, joyce), superior(james, alicia), superior(james, ahmad). For all other possible (X, Y) combinations superior(X, Y) is false. Jan. 2012 Yangjun Chen ACS-3902 15

Deductive Databases The above interpretation is also a model for the rules (1) and (2) since each of them evaluates always to true under the interpretation. For example, superior(X, Y) supervise(X, Y) superior(franklin, john) supervise(franklin, john) is true. superior(franklin, ramesh) supervise(franklin, ramesh) is true. . … superior(X, Y) supervise(X, Z), superior(Z, Y) superior(james, ramesh) supervise(james, franklin), superior (franklin, ramesh) is true. superior(james, alicia) supervise(james, jennifer), superior (jennifer, alicia) is true. Jan. 2012 Yangjun Chen ACS-3902 16

Deductive Databases The model is also the minimal model for the rule (1) and (2) and the corresponding facts since eliminating any element from the model will make some facts or instatiated rules evaluate to false. For example, eliminating supervise(franklin, john) from the model will make this fact no more true under the interpretation; eliminating superior (james, ramesh) will make the following rule no more true under the interpretation: superior(james, ramesh) supervise(james, franklin), superior(franklin, ramesh) Jan. 2012 Yangjun Chen ACS-3902 17

Deductive Databases - Inference mechanism In general, there are two approaches to evaluating logical programs: bottom-up and top-down. - Bottom-up mechanism (also called forward chaining and bottom-up resolution) 1. The inference engine starts with the facts and applies the rules to generate new facts. That is, the inference moves forward from the facts toward the goal. 2. As facts are generated, they are checked against the query predicate goal for a match. Jan. 2012 Yangjun Chen ACS-3902 18

Deductive Databases - Example query goal: superior(james, Y)? rules and facts are given as above. 1. Check whether any of the existing facts directly matches the query. 2. Apply the first rule to the existing facts to generate new facts. 3. Apply the second rule to the existing facts to generate new facts. 4. As each fact is gnerated, it is checked for a match of the query goal. 5. Repeat step 1 - 4 until no more new facts can be found. All the facts of the form: superior(james, a) are the answers. Jan. 2012 Yangjun Chen ACS-3902 19

Deductive Databases - Example: 1. superior(X, Y) supervise(X, Y). 2. superior(X, Y) supervise(X, Z), superior(Z, Y). (rule 1) (rule 2) known facts: supervise(franklin, john), supervise(franklin, ramesh), supervise(franklin, joyce), supervise(james, franklin), supervise(jennifer, alicia), supervise(jennifer, ahmad), supervise(james, jennifer). For all other possible (X, Y) combinations supervise(X, Y) is false. domain = {james, franklin, john, ramesh, joyce, jennifer, alicia, ahmad} superior(james, Y)? applying the first rule: superior(james, franklin), superior(james, jennifer) Y = {franklin, jennifer} applying the second rule: Y = {John, Joyce, Ramesh, alicia, ahmad} Jan. 2012 Yangjun Chen ACS-3902 20

Deductive Databases Top-down mechanism (also called back chaining and top-down resolution) 1. The inference engine starts with the query goal and attempts to find matches to the variables that lead to valid facts in the database. That is, the inference moves backward from the intended goal to determine facts that would satisfy the goal. 2. During the course, the rules are used to generate subgoals. The matching of these subgoals will lead to the match of the intended goal. Jan. 2012 Yangjun Chen ACS-3902 21
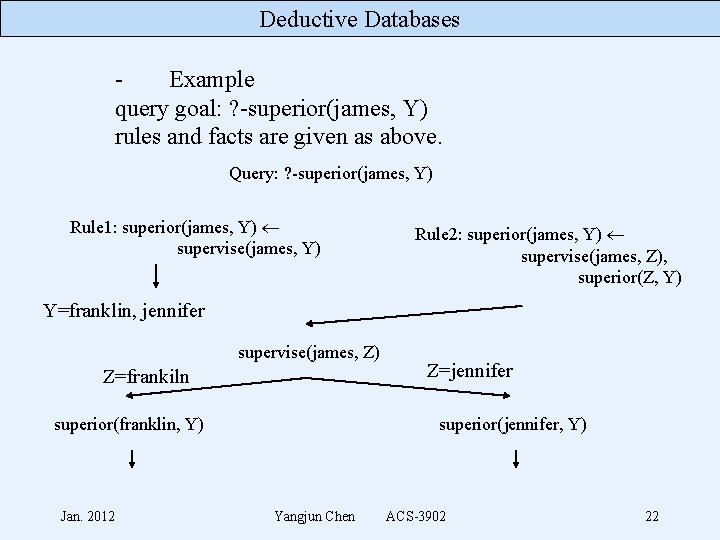
Deductive Databases Example query goal: ? -superior(james, Y) rules and facts are given as above. Query: ? -superior(james, Y) Rule 1: superior(james, Y) supervise(james, Y) Rule 2: superior(james, Y) supervise(james, Z), superior(Z, Y) Y=franklin, jennifer supervise(james, Z) Z=frankiln superior(franklin, Y) Jan. 2012 Z=jennifer superior(jennifer, Y) Yangjun Chen ACS-3902 22

Deductive Databases Rule 1: superior(franklin, Y) supervise(franklin, Y) Rule 1: superior(jennifer, Y) supervise(jennifer, Y) Y= alicia, ahmad Y= john, ramesh, joyce Jan. 2012 Yangjun Chen ACS-3902 23

Deductive Databases • Datalog programs and their evaluation 1. A Datalog program is a logic program. 2. In a Datalog program, each predicate contains no function symbols. 3. A Datalog program normally contains two kinds of predicates: fact-based predicates and rule-based predicates. fact-based predicates are defined by listing all the combinations of values that make the predicate true. Rule-based predicates are defined to be the head of one or more Datalog rules. They correspond to virtual relations whose contents can be inferred by the inference engine. Jan. 2012 Yangjun Chen ACS-3902 24

Deductive Databases • Datalog programs and their evaluation Example: - All the programs discussed earlier are Datalog programs. superior(X, Y) supervise(X, Y). superior (X, Y) supervise(X, Z), superior (Z, Y). supervise(jennifer, ahmad). supervise(james, jennifer). - The following is a logic program, but not a Datalog program: p(X, Y) q(f(Y), X) Jan. 2012 Yangjun Chen ACS-3902 25

Deductive Databases • Datalog programs and their evaluation two important concepts: - safety of programs - predicate dependency graph Jan. 2012 Yangjun Chen ACS-3902 26

Deductive Databases • Datalog programs and their evaluation - Safety of programs A Datalog program or a rule is said to be safe if it generates a finite set of facts. - Condition of unsafty A rule is unsafe if one of the variables in the rule can range over an infinite domain of values, and that variable is not limited to ranging over a finite predicate before it is instantiated. - Example: big_salary(Y) Y > 60000, employee(X), salary(X, Y). Jan. 2012 Yangjun Chen ACS-3902 27

Deductive Databases • Datalog programs and their evaluation - Example: ? -big_salary(Y) Y > 60000, employee(X), salary(X, Y). The evaluation of these rules (no matter whether in bottomup or in top-down fashion) will never terminate. The following is a safe rule: big_salary(Y) employee(X), salary(X, Y), Y > 60000. Jan. 2012 Yangjun Chen ACS-3902 28

Deductive Databases • Datalog programs and their evaluation A variable X is limited if (1) it appears in a regular (not built-in) predicate in the body of the rule. (built-in predicates: <, >, , , =, ) (2) it appears in a predicate of the form X = c or c = X, where c is a constant. (3) it appears in a predicate of the form X = Y or Y = X in the rule body, where Y is a limited variable. (4) Before it is instantiated, some other regular predicates containing it will have been evaluated. - Condition of safty: A rule is safe if each variable in it is limited. A program is safe if each rule in it is safe. Jan. 2012 Yangjun Chen ACS-3902 29

Deductive Databases • Datalog programs and their evaluation - predicate dependency graphs For a program P, we construct a dependency graph G representing a refer to relationship between the predicates in P. This is a directed graph where there is node for each predicate and an arc from node q to node p if and only if the predicate q occurs in the body of a rule whose head predicate is p. Exampel: superior(X, Y) supervise(X, Y), superior(X, Y) supervise(X, Z), superior(Z, Y), subordinary(X, Y) superior(Y, X), supervisor(X, Y) employee(X), supervise(X, Y), over_40 K_emp(X) employee(X), salary(X, Y), Y 40000, under_40 K_supervisor(X) supervisor(X), not(over_40 K_emp(X)), main_productx _emp(X ) employee(X), workson(X, productx, Y), Y 20, president(X) employee(X), not(supervise(Y, X)). Jan. 2012 Yangjun Chen ACS-3902 30

Deductive Databases • Datalog programs and their evaluation - predicate dependency graphs supervisor under_40 K_supervisor main_poductx_emp subordinate president over_40 K_emp superior Jan. 2012 workson employee salary supervise department project female Yangjun Chen ACS-3902 31

Deductive Databases • Datalog programs and their evaluation Evaluation of nonrecursive rules - Jan. 2012 If the dependency graph for a rule set has no cycles, the rule set is nonrecursive. Yangjun Chen ACS-3902 32

Deductive Databases • Datalog programs and their evaluation - Evaluation of nonrecursive rules - evaluation involving only fact-based predicates ? -salary(X, 60000) $1 ( $2 = “ 60000”(salary)) - evaluation involving only rule-based predicates 1. rule rectification h(X, c) . . . h(X, Y) . . . , Y=c h(X, X) . . . Jan. 2012 Yangjun Chen h(X, Y) . . . , Y=X ACS-3902 33

Deductive Databases • Datalog programs and their evaluation - evaluation involving only rule-based predicate 2. Single rule evaluation To evaluate a rule of the from: p p 1, . . . , pn we first compute the relations corresponding to p 1, . . . , pn and then the relation corresponding to p. 3. Jan. 2012 All the rules will be evaluated along the predicate dependency graph. At each step, each rule will be evaluated in terms of step (2). Yangjun Chen ACS-3902 34

Deductive Databases • Datalog programs and their evaluation - The general bottom-up evaluation strategy for a nonrecursive query ? -p(x 1, x 2, …, xn) 1. Locate a set of rules S whose head involves the predicate p. If there are no such rules, then p is a fact-based predicate corresponding to some database relation Rp; in this case, one of the following expression is returned and the algorithm is terminated. (We use the notation $i to refer to the name of the i-th attribute of relation Rp. ) (a) If all arguments in p are distinc variables, the relational expression returned is Rp. (b) If some arguments are constants or if the same variable appears in more than one argument position, the expression returned is SELECT<condition>(Rp), Jan. 2012 Yangjun Chen ACS-3902 35

Deductive Databases where the <condition> is a conjunctive condition made up of a number of simple conditions connected by AND, and constructed as follows: i. if a constant c appears as argument i, include a simple condition ($i = c) in the conjuction. ii. if the same variable appears in both argument location j and k, include a condition ($j = $k) in the conjuction. 2. At this point, one or more rules Si, i = 1, 2, . . . , n, n > 0 exist with predicate p as their head. For each such rule Si, generate a relational expression as follows: a. Apply selection operation on the predicates in the body for each such rule, as discussed in Step 1(b). b. A natural join is constructed among the relations that correspond to the predicates in the body of the rule Si over the common variables. Let the resulting relation from this join be Rs. Jan. 2012 Yangjun Chen ACS-3902 36

Deductive Databases c. If any built-in predicate X Y was defined over the arguments X and Y, the result of the join is subjected to an additional selection: SELECT X Y(Rs) d. Repeat Step 2(c) until no more built-in predicates apply. 3. Take the UNION of the expressions generated in Step 2 (if more than one rule exists with predicate p as its head. ) Jan. 2012 Yangjun Chen ACS-3902 37

Deductive Databases • Datalog programs and their evaluation Evaluation of recursive rules - If the dependency graph for a rule set has at least one cycle, the rule set is recursive. ancestor(X, Y) parent(X, Y), ancestor(X, Y) parent(X, Z), ancestor(Z, Y). - naive strategy - semi-naive strategy - stratified databases Jan. 2012 Yangjun Chen ACS-3902 38

Deductive Databases • Datalog programs and their evaluation - some teminology for recursive queries - - linearly recursive - left linearly recursive ancestor(X, Y) ancestor(X, Z), parent(Z, Y) right linearly recursive ancestor(X, Y) parent(X, Z), ancestor(Z, Y) - non-linearly recursive sg(X, Y) sg(X, Z), sibling(Z, W), sg(W, Y) Jan. 2012 Yangjun Chen ACS-3902 39

Deductive Databases • Datalog programs and their evaluation - some teminology for recursive queries - extensional database (EDB) predicate An EDB predicate is a predicate whose relation is stored in the database - fact-based predicate. - intensional database (IDB) predicate An IDB predicate is a predicate whose relation is defined by logic rules - rule-based predicate. - Datalog equation A Datalog equation is an equation obtained by replacing “ ” and “ ” with “=” and “ ” in a rule, respectively. a(X, Y) = p(X, Y) X, Y(p(X, Z) Jan. 2012 Yangjun Chen ACS-3902 a(Z, Y)) 40

Deductive Databases • Datalog programs and their evaluation - some teminology for recursive queries - fixed point Consider a relation sequence: g 0, g 1, …, gi+1, . . . g 0 = , gi+1 = E(gi), If there exits some g such that g = E(g), g is called the fixed point. The least among all fixed points of E(. . . ) is called the least fixed point. - evaluation of fixed points E i(g 0) = E (E(. . . E(g 0). . . )) i Jan. 2012 Yangjun Chen If at some time we have E i(g 0) = E i+1(g 0), then E i(g 0) is the fixed point of the function E(. . . ). It is also the least fixed point of E(. . . ). ACS-3902 41

Deductive Databases • Datalog programs and their evaluation - some teminology for recursive queries - fixed point Example: a(X, Y) = p(X, Y) X, Y(p(X, Z) a(Z, Y)) p = {(f, j), (f, r), (f, jo), (je, ah), (ja, f), (ja, je)} a 0 = { } a 1 = {(f, j), (f, r), (f, jo), (je, ah), (ja, f), (ja, je)} a 2 = {(f, j), (f, r), (f, jo), (je, ah), (ja, f), (ja, je), (ja, j), (ja, r), (ja, jo), (ja, ah)} a 3 = a 2 least fixed point The least fixed point of the above equation is also called the transitive closure of p. Jan. 2012 Yangjun Chen ACS-3902 42

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - naive strategy 1. The naive evaluation method is a bottom-up strategy which computes the least model of a Datalog program. 2. It is an iterative strategy and at each iteration all rules are applied to the set of tuples produced thus far to generate all implicit tuples. 3. This iterative process continues until no more new tuples can be produced. Jan. 2012 Yangjun Chen ACS-3902 43

Deductive Databases • Datalog programs and their evaluation - naive strategy Consider the following equation system: Ri = Ei(R 1, . . . , Ri, . . . , Rn) (i = 1, . . . , m) which is formed by replacing the symbol with an equality sign in a Datalog program. Algorithm Jacobi naive strategy input: A system of algebraic equations and EDB. output: The values of the variable relations: R 1, . . . , Ri, . . . , Rn. for i = 1 to n do Ri : = ; repeat Con : = true; for i = 1 to n do Si : = Ri; for i = 1 to m do {Ri : = Ei(S 1, . . . , Si, . . . , Sn); if Ri Si then {Con : = false; Si : = Ri; }} until Con = true; Jan. 2012 Yangjun Chen ACS-3902 44

Deductive Databases • Datalog programs and their evaluation - naive strategy sg(X, Y) sg(X, W), sibling(W, Z), sg(Z, Y) sibling(X, Y) parent(X, W), sibling(W, Z), parent(Y, Z) sg(X, Y) = X, Y(sg(X, W) sibling(W, Z) sibling(X, Y) = X, Y(parent(X, W) sg(Z, Y)) sibling(W, Z) sg = E 1(sg, sibling) sibling = E 2(sibling) parent(Y, Z)) sg R 1 R 2 sibling R 1 = E 1(R 1, R 2) R 2 = E 2(R 2) Jan. 2012 Yangjun Chen ACS-3902 45
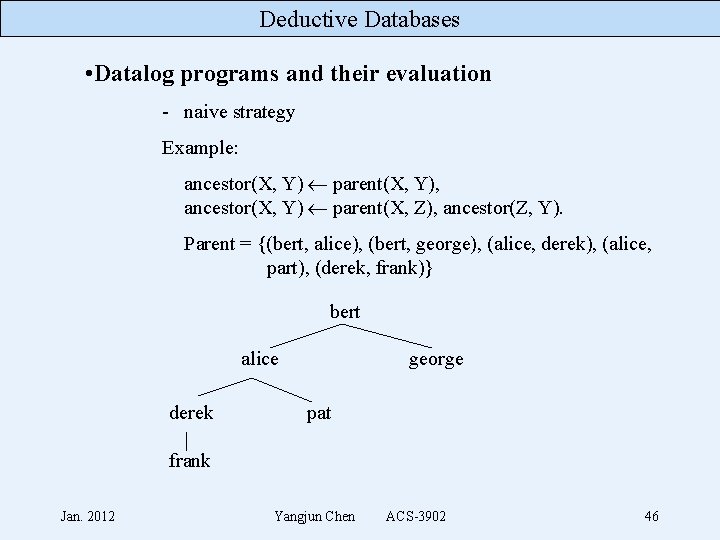
Deductive Databases • Datalog programs and their evaluation - naive strategy Example: ancestor(X, Y) parent(X, Y), ancestor(X, Y) parent(X, Z), ancestor(Z, Y). Parent = {(bert, alice), (bert, george), (alice, derek), (alice, part), (derek, frank)} bert alice derek george pat frank Jan. 2012 Yangjun Chen ACS-3902 46

Deductive Databases • Datalog programs and their evaluation - naive strategy Example: A(X, Y) = X, Y(P(X, Z) A(Z, Y)) P(X, Y) step 0: A 0 = step 1: A 1 = {(bert, alice), (bert, george), (alice, derek), (alice, part), (derek, frank)} step 2: A 2 = {(bert, alice), (bert, george), (alice, derek), (alice, part), (derek, frank), (bert, derek), (bert, pat), (alice, frank)} step 3: A 3 = {(bert, alice), (bert, george), (alice, derek), (alice, part), (derek, frank), (bert, derek), (bert, pat), (alice, frank), (bert, frank)} step 4: Jan. 2012 A 4 = A 3 Yangjun Chen ACS-3902 47

Deductive Databases • Datalog programs and their evaluation - naive strategy Algorithm Gauss-Seidel naive strategy Jacobi: Gauss-Seidel: k-th iteration: R 1(k) = E 1(R 1 (k-1), . . . , Ri (k-1), . . . , Rn (k-1)), …… Ri(k) = Ei(R 1 (k-1), . . . , Ri (k-1), . . . , Rn (k-1)), …… Rn(k) = En(R 1 (k-1), . . . , Ri (k-1), . . . , Rn (k-1)). Jan. 2012 Yangjun Chen R 1(k) = E 1(R 1 (k-1), . . . , Ri (k-1), . . . , Rn (k-1)), …… Ri(k) = Ei(R 1 (k), . . . , Ri (k-1), . . . , Rn (k-1)), …… Rn(k) = En(R 1 (k), . . . , Ri (k), . . . , Rn (k-1)). ACS-3902 48

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - semi-naive strategy 1. The semi-naive evaluation method is a bottom-up strategy. 2. It is designed to eliminate redundancy in the evaluation of tuples at different iterations. Let Ri(k) be the temporary value of relation Ri at iteration step k. The differential of Ri between step k and step k - 1 is defined as follows: Di(k) = Ri(k) - Ri(k-1) For a linearly recursive rule set, Di(k) can be substituted for Ri in the k-th iteration of the naïve algorithm. 3. The result is obtained by the union of the newly obtained term Ri and that obtained in the previous step. Jan. 2012 Yangjun Chen ACS-3902 49

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - semi-naive strategy Algorithm seminaiv strategy input: A system of algebraic equations and EDB. output: The values of the variable relations: R 1, . . . , Ri, . . . , Rn. for i = 1 to n do Ri : = ; for i = 1 to m do Di : = ; repeat Con : = true; for i = 1 to n do {Di : = E(D 1, . . . , Di, . . . , Dn) - Ri; Ri : = Di Ri; if Di then Con : = false; } until Con is true; Jan. 2012 Yangjun Chen ACS-3902 50

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - semi-naive strategy Example: Step 0: D 0 = , A 0 = ; Step 1: D 1 = P = {(bert, alice), (bert, george), (alice, derek), (alice, part), (derek, frank)} A 1 = D 1 A 0 = {(bert, alice), (bert, george), (alice, derek), (alice, part), (derek, frank)} Step 2: D 2 = {(bert, derek), (bert, pat), (alice, frank)} A 2 = D 2 A 1 = {(bert, alice), (bert, george), (alice, derek), (alice, part), (derek, frank), {(bert, derek), (bert, pat), (alice, frank)} Jan. 2012 Yangjun Chen ACS-3902 51

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - semi-naive strategy Example: Step 3: D 3 = {(bert, frank) A 3 = D 3 A 2 = {(bert, alice), (bert, george), (alice, derek), (alice, part), (derek, frank), {(bert, derek), (bert, pat), (alice, frank), (bert, frank)} Step 3: D 4 = . The advantage of the semi-naive method is that at each step a differential term Di is used in each equation instead of the whole Ri. In this way, the time complexity of a computation is decreased drastically. Jan. 2012 Yangjun Chen ACS-3902 52

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - The magic-set rule rewriting technique motivation: 1. During a bottom-up evaluation, too many irrelevant tuples are evaluated. For example, to evaluate the query sg(john, Z)? using the following rules: sg(X, Y) flat(X, Y), sg(X, Y) up(X, Z), sg(Z, W), down(W, Y), a bottom-up method will generate all sg-tuples and then makes a selection operation to the anwsers. 2. Using the constants appearing in the query to restrict computation. Jan. 2012 Yangjun Chen ACS-3902 53

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - The magic-set rule rewriting technique les d ru e i f i d o M les Magic ru sg(X, Y) magic_sg(X) , flat(X, Y), sg(X, Y) magic_sg(X), up(X, Z), sg(Z, W), down(W, Y), magic_sg(Z) magic_sg(X), up(X, Z), magic_sg(john). Two-phase evaluation: 1 st phase: evaluate magic rules to generate a magic set. 2 nd phase: evaluate modified rules, by which that magic set is used to restrict the computation. Jan. 2012 Yangjun Chen ACS-3902 54

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - Stratified databases A stratified database is a Datalog program containing negated predicates. Example: Suppose that a supplier might wish to backorder items that are not in the warehouse. It would be convenient to write: backorder(X) item(X), warehouse(X). Its logically equivalent form is backorder(X), warehouse item(X). But this rule has a different meaning : if X is an item, then backorder it or it is stored in the warehouse. This is not what we want. Jan. 2012 Yangjun Chen ACS-3902 55

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - Stratified databases - Prolblem: recursion via negation p(X) q(X), q(X) p(X). - To avoid the recursion via negation, we introduce the concept of stratification, which is defined by the use of a level l mapping: assign each literal in the program an integer such that if B A 1, …, An and Ai is positive, then l(Ai) l(B) for all i, 1 i n. If Ai is negative, then l(B) < l(Ai) for all i, 1 i n. Jan. 2012 Yangjun Chen ACS-3902 56

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - Stratified databases - Prolblem: recursion via negation p(X) q(X), q(X) p(X). - To avoid the recursion via negation, we introduce the concept of stratification, which is defined by the use of a level l mapping: assign each literal in the program an integer such that if B A 1, …, An and Ai is positive, then l(Ai) l(B) for all i, 1 i n. If Ai is negative, then l(B) < l(Ai) for all i, 1 i n. Jan. 2012 Yangjun Chen ACS-3902 57

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - Stratified databases - If you can assign integers to all the literals in a programusing a level mapping, then this program is stratifiable. p(X) q(X), q(X) p(X). In fact, we cannot find a level mapping for any program which contains recursion via negation. - Evaluation of a stratified database. Evaluate the literals in the program from low level to the high level. Jan. 2012 Yangjun Chen ACS-3902 58

Deductive Databases • Datalog programs and their evaluation - evaluation of recursive queries - Stratified databases - However, you cannot find any level mapping for the following program: Example: path(X, Y) edge(X, Y), path(X, Y) edge(X, Z), path(Z, Y), acyclic_path(X, Y) path(X, Y), path(Y, X). We can many label mappings for this program. The following are just two of them: Jan. 2012 Yangjun Chen ACS-3902 59
- Slides: 59