Decomposition Method 1 Types of Data w Time

Decomposition Method 1

Types of Data w Time series data: a sequence of observations measured over time (usually at equally spaced intervals, e. g. , weekly, monthly and annually). Examples of time series data include: Gross Domestic Product each quarter; annual rainfall; daily stock market index w Cross sectional data: data on one or more variables collected at the same point in time 2

Time Series vs Causal Modeling w Causal (regression) models: the investigator specifies some behavioural relationship and estimates the parameters using regression techniques; w Time series models: the investigator uses the past data of the target variable to forecast the present and future values of the variable 3

Time Series vs Causal Modeling w On the other hand, there are many cases when one cannot, or one prefers not to, build causal models: 1. 2. 3. 4. 5. insufficient information is known about the behavioural relationship; lack of, or conflicting, theories; insufficient data on explanatory variables; expertise may be unavailable; time series models may be more accurate 4

Time Series vs Causal Modeling w Direct benefits of using time series models: 1. 2. 3. Little storage capacity is needed; some time series models are automatic in that user intervention is not required to update the forecasts each period; some time series models are evolutionary in that the models adapt as new information is received; 5

Classical Decomposition of Time Series w Trend – does not necessarily imply a monotonically increasing or decreasing series but simply a lack of constant mean, though in practice, we often use a linear or quadratic function to predict the trend; w Cycle – refers to patterns or waves in the data that are repeated after approximately equal intervals with approximately equal intensity. For example, some economists believe that “business cycles” repeat themselves every 4 or 5 years; 6

Classical Decomposition of Time Series w Seasonal – refers to a cycle of one year duration; w Random (irregular) – refers to the (unpredictable) variation not covered by the above 7

Decomposition Method w Multiplicative Models w Additive Models Find the estimates of these four components. 8

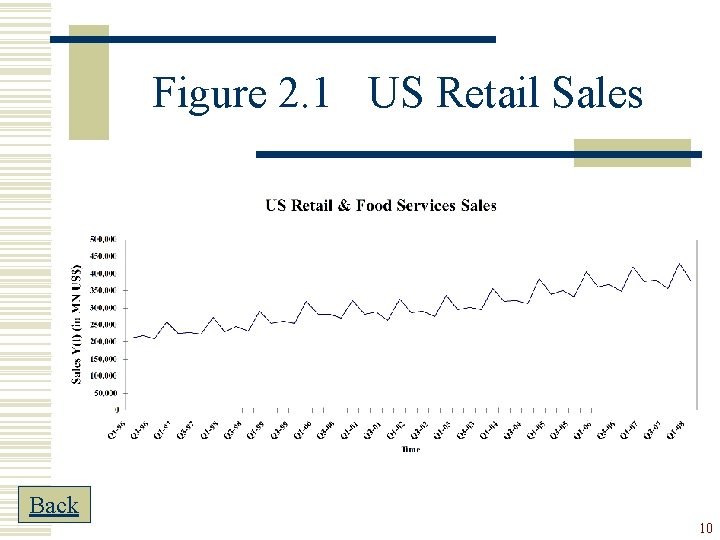
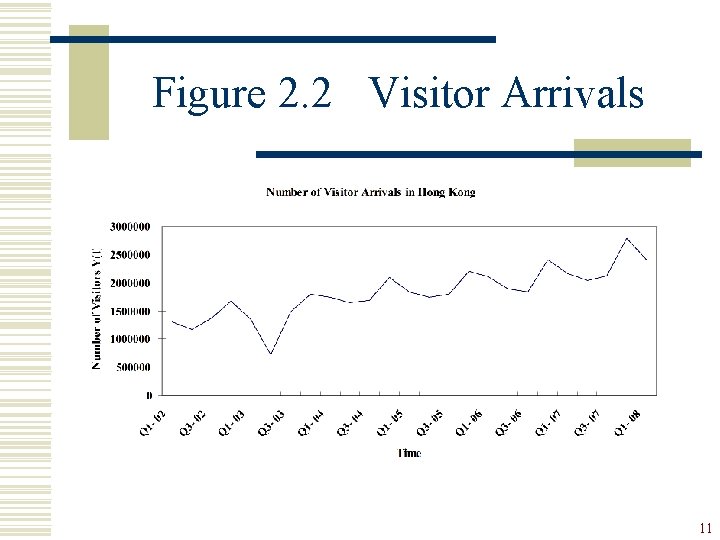
Multiplicative Decomposition w Examples: (1) US Retail and Food Services Sales from 1996 Q 1 to 2008 Q 1 Figure 2. 1 (2) Quarterly Number of Visitor Arrivals in Hong Kong from 2002 Q 1 to 2008 Q 1 Figure 2. 2 9

Figure 2. 1 US Retail Sales Back 10

Figure 2. 2 Visitor Arrivals 11

w Cycles are often difficult to identify with a short time series. w Classical decomposition typically combines cycles and trend as one entity: 12

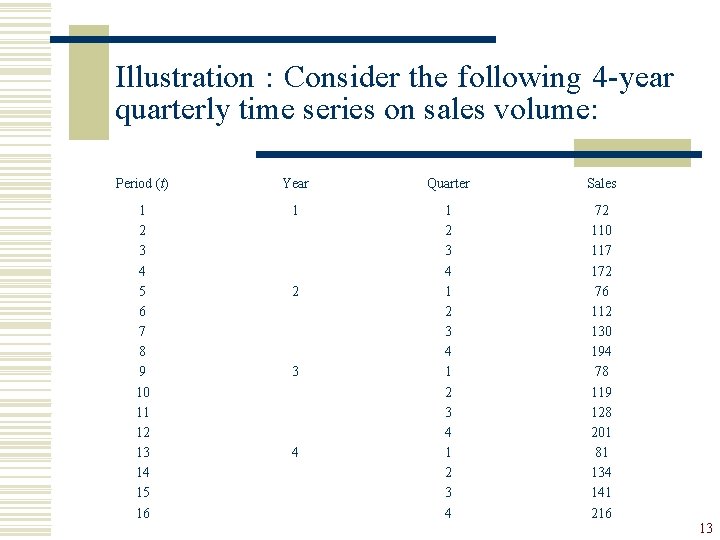
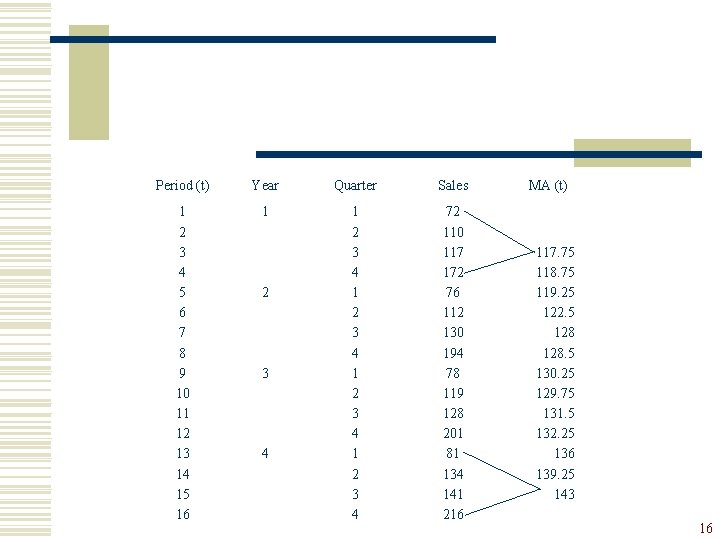
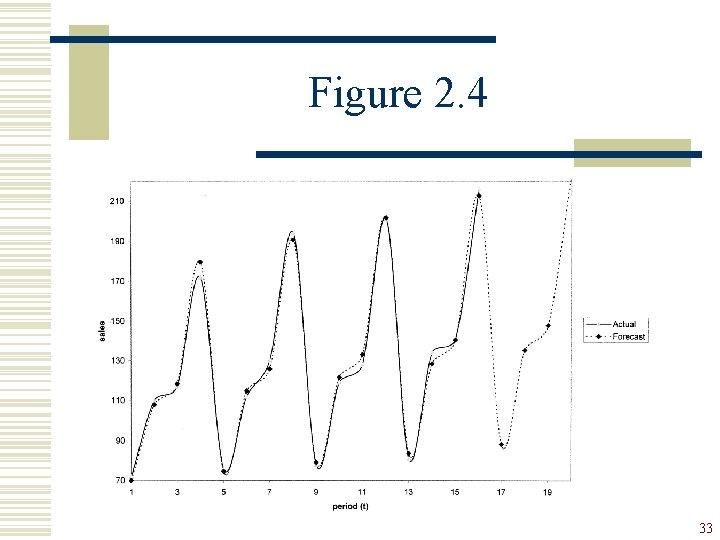
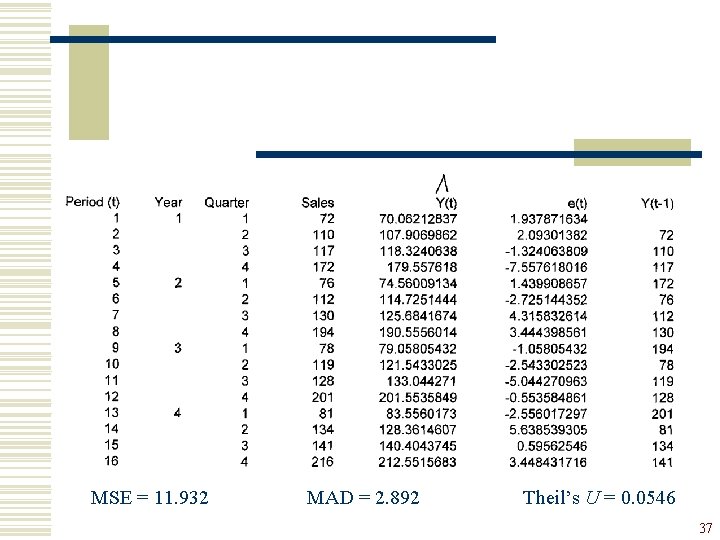
Illustration : Consider the following 4 -year quarterly time series on sales volume: Period (t) Year Quarter Sales 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 1 2 3 4 72 110 117 172 76 112 130 194 78 119 128 201 81 134 141 216 2 3 4 13

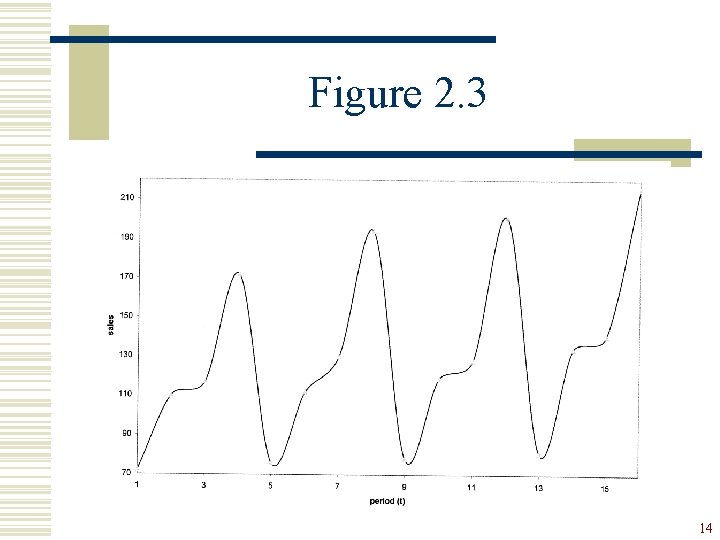
Figure 2. 3 14

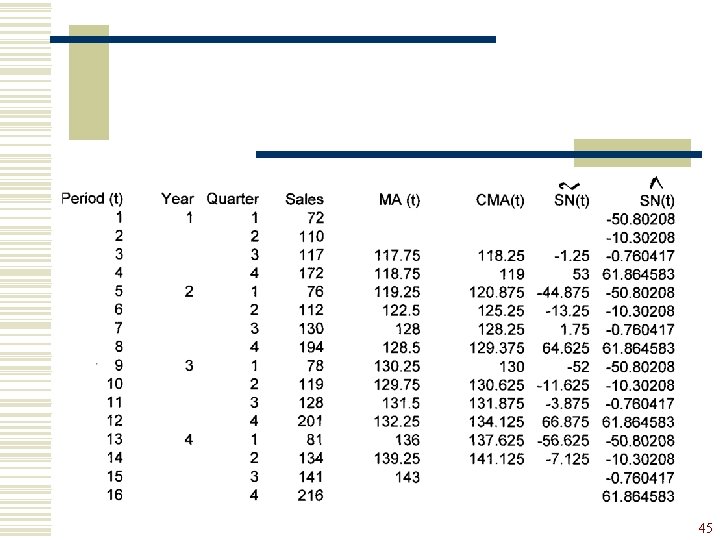
Step 1 : Estimation of seasonal component (SNt) w Yt = TCt SNt IRt w Moving Average for periods 1 – 4 Moving Average for periods 2 – 5 15

Period (t) Year Quarter Sales 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 1 2 3 4 72 110 117 172 76 112 130 194 78 119 128 201 81 134 141 216 2 3 4 MA (t) 117. 75 118. 75 119. 25 122. 5 128. 5 130. 25 129. 75 131. 5 132. 25 136 139. 25 143 16

w Assuming the average of the observations is also the median of the observations, the MA for periods 1 – 4, 2 – 5, 3 – 6 are centered at positions 2. 5, 3. 5 and 4. 5 respectively. 17

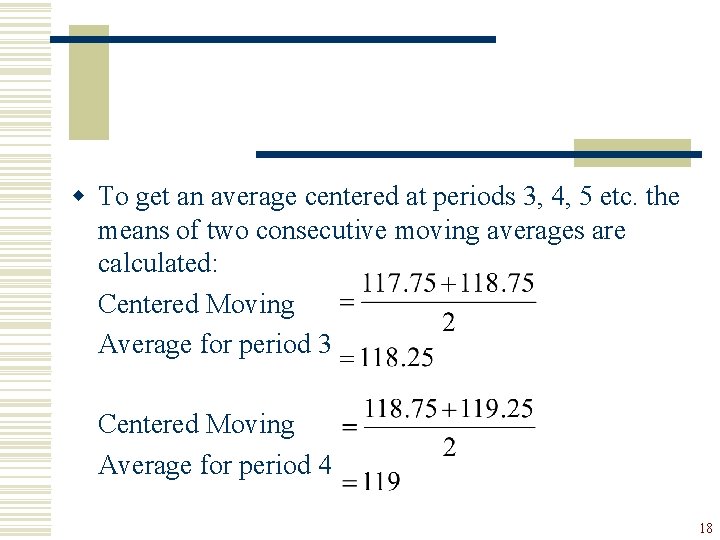
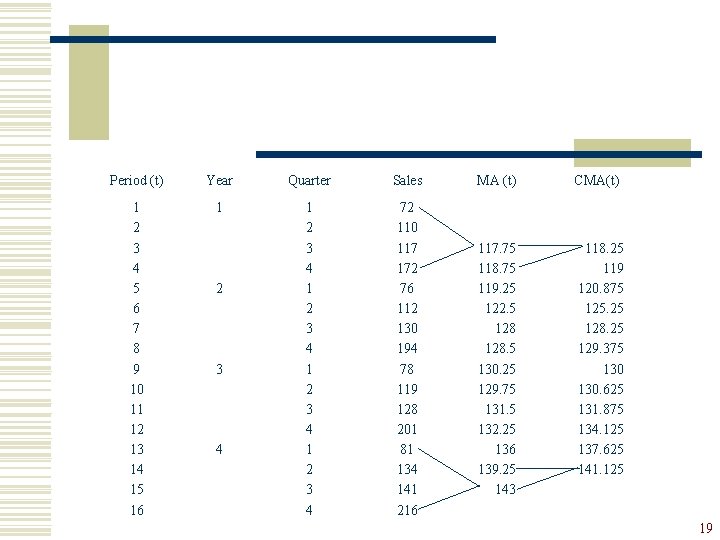
w To get an average centered at periods 3, 4, 5 etc. the means of two consecutive moving averages are calculated: Centered Moving Average for period 3 Centered Moving Average for period 4 18

Period (t) Year Quarter Sales 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 1 2 3 4 72 110 117 172 76 112 130 194 78 119 128 201 81 134 141 216 2 3 4 MA (t) CMA(t) 117. 75 118. 75 119. 25 122. 5 128. 5 130. 25 129. 75 131. 5 132. 25 136 139. 25 143 118. 25 119 120. 875 125. 25 128. 25 129. 375 130. 625 131. 875 134. 125 137. 625 141. 125 19

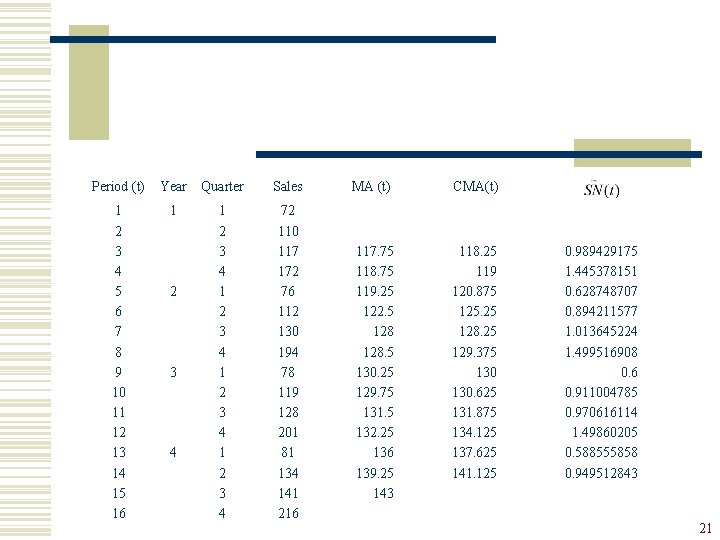
w Because the CMAt contains no seasonality and irregularity, the seasonal component may be estimated by 20

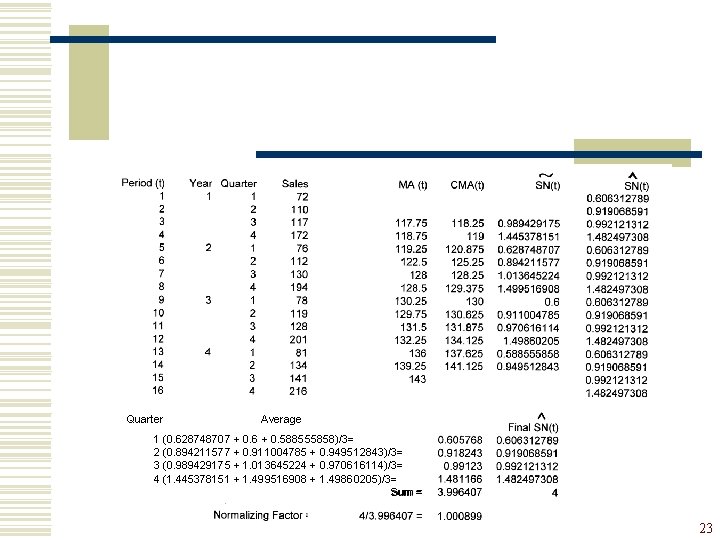
Period (t) Year Quarter Sales 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 1 2 3 4 72 110 117 172 76 112 130 194 78 119 128 201 81 134 141 216 2 3 4 MA (t) CMA(t) 117. 75 118. 75 119. 25 122. 5 128. 5 130. 25 129. 75 131. 5 132. 25 136 139. 25 143 118. 25 119 120. 875 125. 25 128. 25 129. 375 130. 625 131. 875 134. 125 137. 625 141. 125 0. 989429175 1. 445378151 0. 628748707 0. 894211577 1. 013645224 1. 499516908 0. 6 0. 911004785 0. 970616114 1. 49860205 0. 588555858 0. 949512843 21

w After all have been computed, they are further averaged to eliminate irregularities in the series. We also adjust the seasonal indices so that they sum to the number of seasons in a year (i. e. , 4 for quarterly data, 12 for monthly data). Why? ) 22

Quarter Average 1 (0. 628748707 + 0. 6 + 0. 588555858)/3= 2 (0. 894211577 + 0. 911004785 + 0. 949512843)/3= 3 (0. 989429175 + 1. 013645224 + 0. 970616114)/3= 4 (1. 445378151 + 1. 499516908 + 1. 49860205)/3= Sum = 23

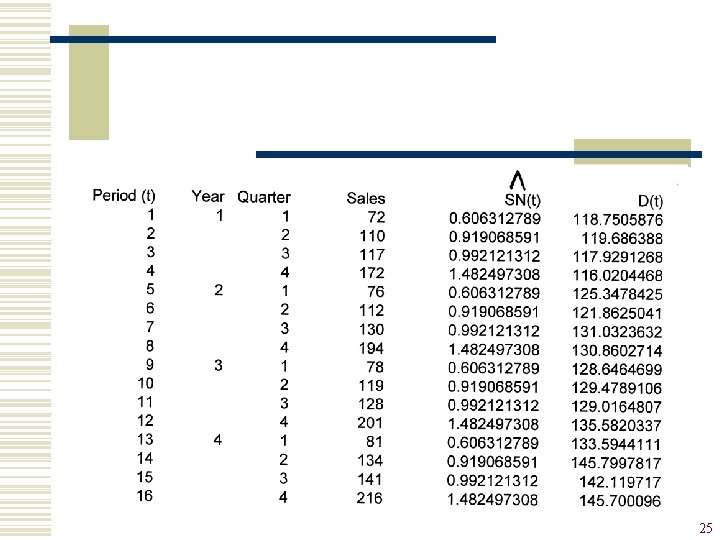
Step 2 : Estimation of Trend/Cycle w Define deseasonalized (or seasonally adjusted) series as for example, D 1 = 72/0. 6063 = 118. 7506 24

25

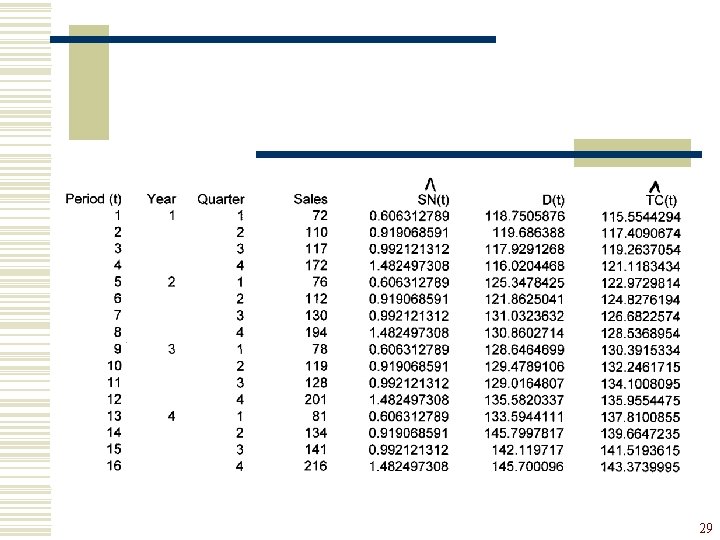
w TCt may be estimated by regression using a linear trend: where b 0 and b 1 are least squares estimates of 0 and 1 respectively. 26

EXCEL regression output : 27

For example, 28

29

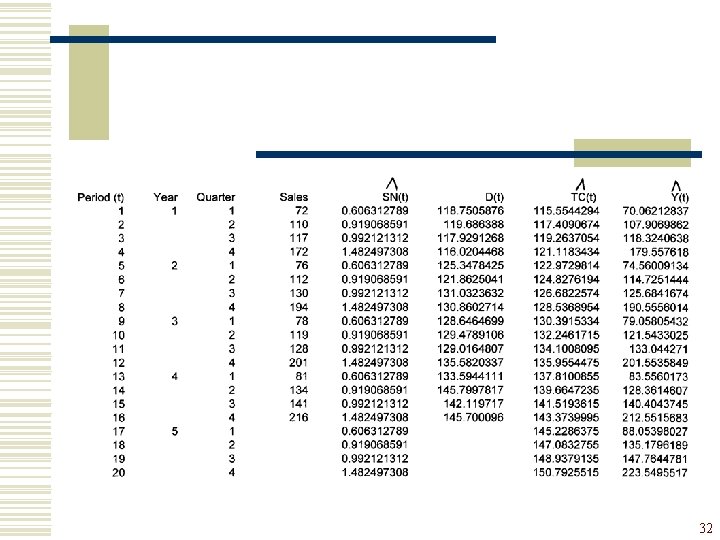
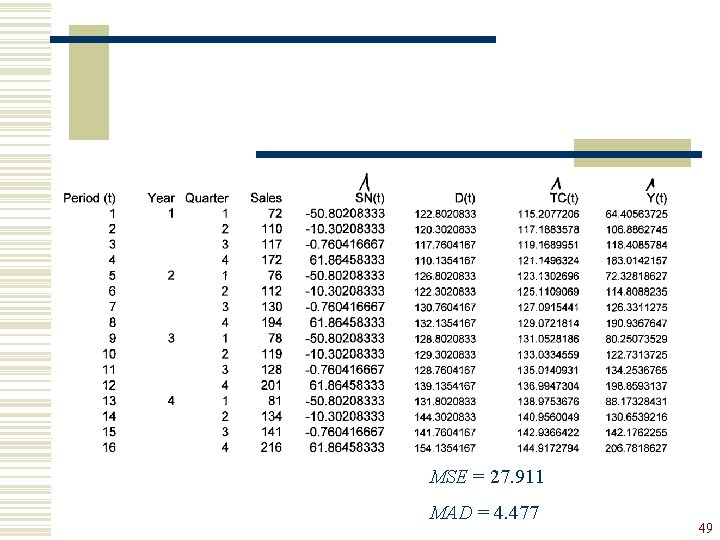
Step 3 : Computation of fitted values and out-of-sample forecasts 30

Out of sample forecast : 31

32

Figure 2. 4 33

Measuring Forecast Accuracy : 1) Mean Squared Error 2) Mean Absolute Deviation 34

et = Method A – 2 1. 5 – 1 2. 1 0. 7 Method B – 4 0. 7 0. 5 1. 4 0. 1 Method A : MSE = MAD = 2. 43 1. 46 Method B : MSE = MAD = 3. 742 1. 34 35

Naive Prediction Theil’s u Statistics if U = 1 Forecasts produced are no better than naive forecast U = 0 Forecasts produced perfect fit The smaller the value of U, the better the forecasts. 36

MSE = 11. 932 MAD = 2. 892 Theil’s U = 0. 0546 37

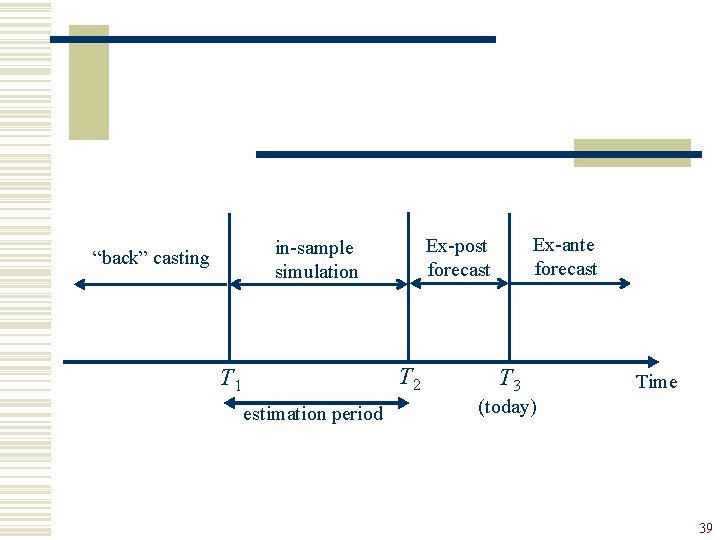
Out-of-Sample Forecasts 1) Expost forecast w Prediction for the period in which actual observations are available 2) Exante forecast w Prediction for the period in which actual observations are not available. 38

“back” casting T 2 T 1 estimation period Ex-ante forecast Ex-post forecast in-sample simulation T 3 Time (today) 39

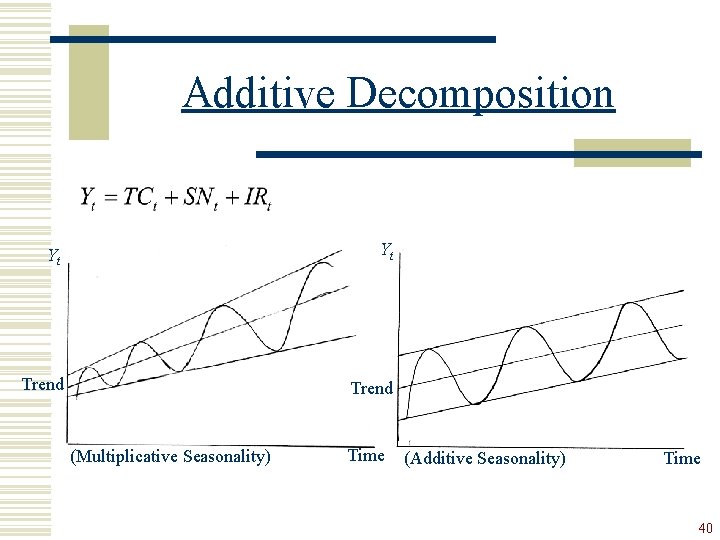
Additive Decomposition Yt Yt Trend (Multiplicative Seasonality) Time (Additive Seasonality) Time 40

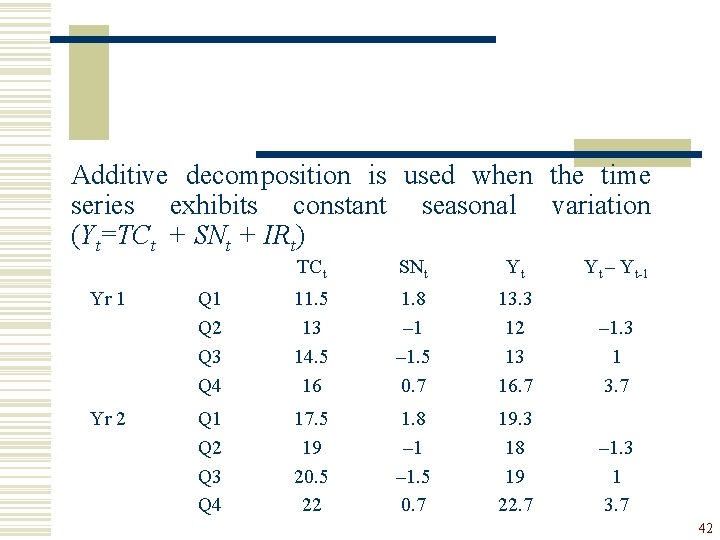
Multiplicative decomposition is used when the time series exhibits increasing or decreasing seasonal variation (Yt=TCt SNt IRt) Yr 1 Yr 2 TCt SNt Yt Yt – Yt-1 Q 2 Q 3 Q 4 11. 5 13 14. 5 16 1. 5 0. 8 1. 2 17. 25 6. 5 11. 6 19. 2 – 10. 75 5. 1 7. 6 Q 1 Q 2 Q 3 Q 4 17. 5 19 20. 5 22 1. 5 0. 8 1. 2 26. 25 9. 5 16. 4 26. 4 – 16. 75 6. 9 10 41

Additive decomposition is used when the time series exhibits constant seasonal variation (Yt=TCt + SNt + IRt) Yr 1 Yr 2 TCt SNt Yt Yt – Yt-1 Q 2 Q 3 Q 4 11. 5 13 14. 5 16 1. 8 – 1. 5 0. 7 13. 3 12 13 16. 7 – 1. 3 1 3. 7 Q 1 Q 2 Q 3 Q 4 17. 5 19 20. 5 22 1. 8 – 1. 5 0. 7 19. 3 18 19 22. 7 – 1. 3 1 3. 7 42

Step 1 : Estimation of seasonal component (SNt) w Calculation of MAt and CMAt is the same as per multiplicative decomposition w Initial seasonal component may be estimated by For example, 43

w Seasonal indices are averaged and adjusted so that they sum to zero (Why? ) 44

45

Step 2 : Estimation of Trend/Cycle w Deseasonalized series is defined as w TCt may be estimated by regression as per multiplicative decomposition 46

i. e. , Dt = o + 1 t + t and Multiplicative decomposition 47

So, and For example, and 48

MSE = 27. 911 MAD = 4. 477 49