Decomposition for Reasoning with Biological Network Gauvain Bourgne

Decomposition for Reasoning with Biological Network Gauvain Bourgne, Katsumi Inoue ISSSB’ 11, Shonan Village, November 13 th -17 th 2011

Motivation In bioinformatics, need to reason on huge amount of data ◦ Huge networks (e. g. metabolic pathways, signaling pathways…) On such problems, centralized methods ◦ Long computation time ◦ Memory overflow Problem decomposition ◦ Divide into smaller problems or steps to recompose a global solution ◦ Need for (1) an automated process to decompose and (2) an algorithm to solve local problems and recompose global solution Automated Problem Decomposition 2 /33
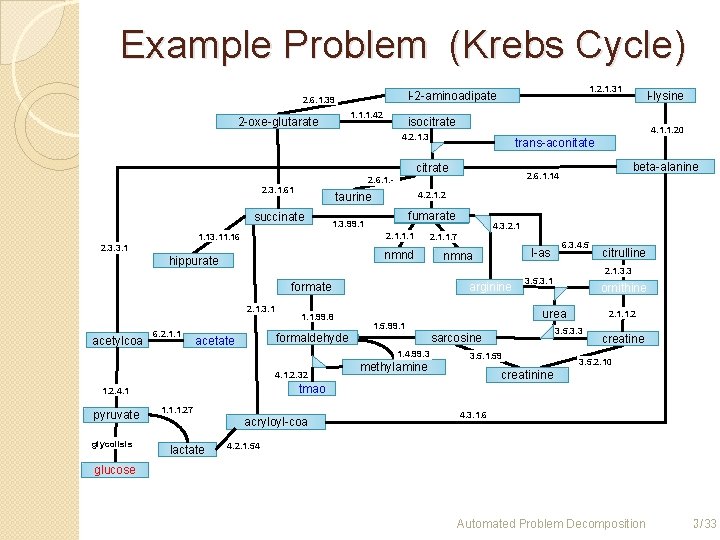
Example Problem (Krebs Cycle) 1. 1. 1. 42 2 -oxe-glutarate 1. 2. 1. 31 l-2 -aminoadipate 2. 6. 1. 39 isocitrate 4. 1. 1. 20 4. 2. 1. 3 trans-aconitate citrate 4. 2. 1. 2 taurine succinate fumarate Fumarate 1. 3. 99. 1 2. 1. 1. 13. 11. 16 2. 3. 3. 1 nmnd hippurate formate 2. 1. 3. 1 acetylcoa 6. 2. 1. 1. 99. 8 glycolisis 6. 3. 4. 5 2. 1. 3. 3 3. 5. 3. 1 ornithine urea methylamine 2. 1. 1. 2 3. 5. 3. 3 sarcosine 3. 5. 1. 59 citrulline creatine 3. 5. 2. 10 creatinine tmao 1. 2. 4. 1 pyruvate l-as nmna 1. 5. 99. 1 1. 4. 99. 3 4. 1. 2. 32 4. 3. 2. 1. 1. 7 arginine formaldehyde acetate beta-alanine 2. 6. 1. 14 2. 6. 1. - 2. 3. 1. 61 l-lysine 1. 1. 1. 27 acryloyl-coa lactate 4. 3. 1. 6 4. 2. 1. 54 glucose 3 Automated Problem Decomposition 3 /33
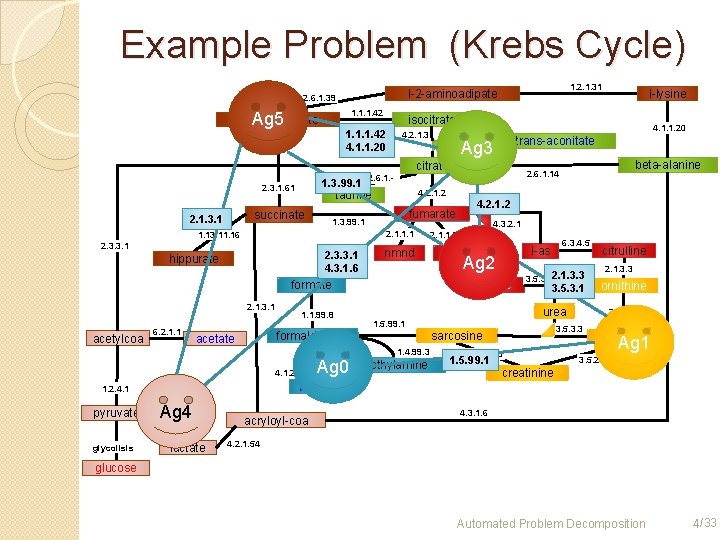
Example Problem (Krebs Cycle) 1. 1. 1. 42 2 -oxe-glutarate Ag 5 1. 2. 1. 31 l-2 -aminoadipate 2. 6. 1. 39 isocitrate 1. 1. 1. 42 4. 1. 1. 20 4. 2. 1. 3 trans-aconitate Ag 3 citrate 1. 3. 99. 1 2. 3. 1. 61 4. 2. 1. 2 2. 1. 1. 1 2. 3. 3. 1 4. 3. 1. 6 hippurate nmnd formate 2. 1. 3. 1 acetylcoa 6. 2. 1. 1. 99. 8 4. 1. 2. 32 glycolisis 6. 3. 4. 5 l-as nmna Ag 2 3. 5. 3. 12. 1. 3. 3 3. 5. 3. 1 urea 1. 5. 99. 1 1. 4. 99. 3 methylamine 3. 5. 1. 59 1. 5. 99. 1 2. 1. 3. 3 ornithine 2. 1. 1. 2 3. 5. 3. 3 sarcosine citrulline creatine Ag 1 3. 5. 2. 10 creatinine tmao 1. 2. 4. 1 pyruvate Ag 0 4. 3. 2. 1. 1. 7 arginine formaldehyde acetate 4. 2. 1. 2 fumarate Fumarate 1. 3. 99. 1 1. 13. 11. 16 beta-alanine 2. 6. 1. 14 2. 6. 1. - taurine succinate 2. 1. 3. 1 l-lysine 1. 1. 1. 27 Ag 4 lactate acryloyl-coa 4. 3. 1. 6 4. 2. 1. 54 glucose 4 Automated Problem Decomposition 4 /33

Overview Reasoning task Partition-based algorithm Automated decomposition Experimental evaluation Conclusion Automated Problem Decomposition 5 /33

Overview Reasoning task Partition-based algorithm Automated decomposition Experimental evaluation Conclusion Automated Problem Decomposition 6 /33

Logical representation Metabolic pathways: set of reactions Ri: m 1, m 2, …, mp p 1, p 2, …, pn Such reactions can be represented as ◦ an activation rule ¬m 1 v¬m 2 v…v¬mp v Ri ◦ n production rules ¬Ri v p 1 ¬Ri v p 2 … ¬Ri v pn Clausal theory Automated Problem Decomposition 7 /33

Problems (Conditional) accessibility problems Sources (si), Conditional sources (ci), Targets (ti) Find which ti can be produced from si, possibly with the addition of ci as a new source ◦ Find all consequences of the form ¬civ…v¬ckv tj Extraction of sub-networks Pathways completion (abduction) ◦ Find reactions (set of clauses) Hypothesis on state of reaction given experiments Problem Decomposition Consequence finding (with. Automated specific form) 8 /33

Main reasoning task Consequence Finding (CF) in clausal theories ◦ Input A clausal theory T A production field P=<L, Cond> L is a list of literals Cond is a condition (maximal length of the consequences, or number of occurrences of some literals) ◦ Output All the consequences of T that are subsumptionminimal and belongs to P (formed with literals of L respecting condition Cond). Carc(T, P) Automated Problem Decomposition 9 /33

Overview Reasoning task Partition-based algorithm Automated decomposition Experimental evaluation Conclusion Automated Problem Decomposition 10/33

Partition-based CF The task ◦ Consequence Finding (CF) in clausal theories Input A set of clausal theory Ti such that UTi=T, and a set of reasoners ai associated with each partition A production field P=<L, Cond> Output Carc(T, P) Where The output should be produced through local computations and interactions between reasoners (message exchange) Automated Problem Decomposition 11/33
![Partition-based Consequence Finding Generalization of Partition-based Theorem Proving [Amir & Mc. Ilraith, 2005] ◦ Partition-based Consequence Finding Generalization of Partition-based Theorem Proving [Amir & Mc. Ilraith, 2005] ◦](http://slidetodoc.com/presentation_image_h2/fb20e1fddc2c1f9a7959ce1eb1b724ac/image-12.jpg)
Partition-based Consequence Finding Generalization of Partition-based Theorem Proving [Amir & Mc. Ilraith, 2005] ◦ Based on Craig’s Interpolation Theorem: If C entails D, then there is a formula F involving only symbols common to C et D such that C entails FCand F entails. FD. D Principles Identify common symbols (communication languages) Build a tree structure (cycle-cut) Forward relevant consequences from leaf to root Automated Problem Decomposition 12/33
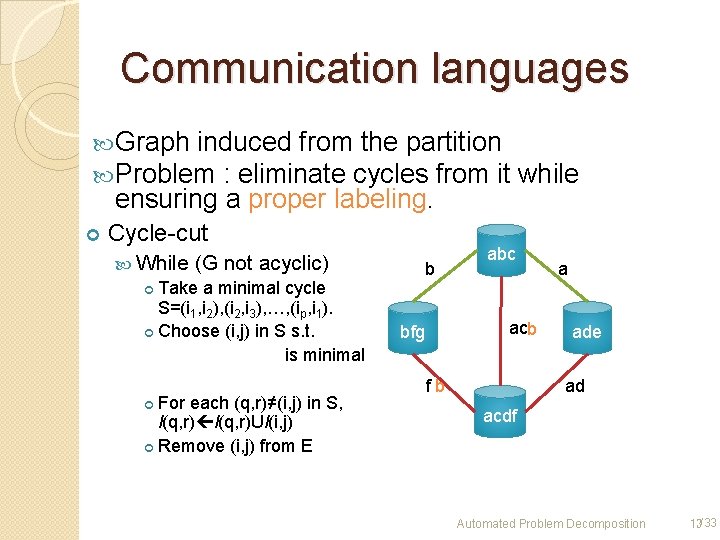
Communication languages Graph induced from the partition Problem : eliminate cycles from it ensuring a proper labeling. Cycle-cut While (G not acyclic) Take a minimal cycle S=(i 1, i 2), (i 2, i 3), …, (ip, i 1). Choose (i, j) in S s. t. is minimal For each (q, r)≠(i, j) in S, l(q, r)Ul(i, j) Remove (i, j) from E b while abc acb bfg fb a ade ad acdf Automated Problem Decomposition 13/33
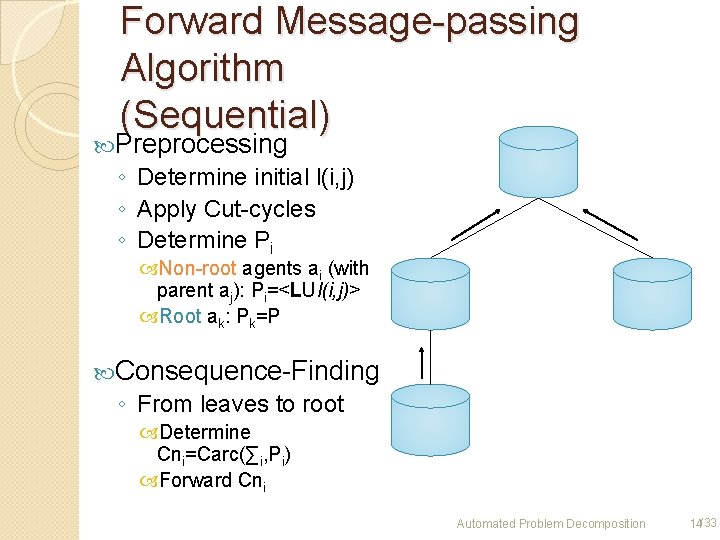
Forward Message-passing Algorithm (Sequential) Preprocessing Carc ◦ Determine initial l(i, j) ◦ Apply Cut-cycles ◦ Determine Pi Non-root agents ai (with parent aj): Pi=<LUl(i, j)> Root ak: Pk=P Carc Consequence-Finding ◦ From leaves to root Determine Cni=Carc(∑i, Pi) Forward Cni Carc Automated Problem Decomposition 14/33
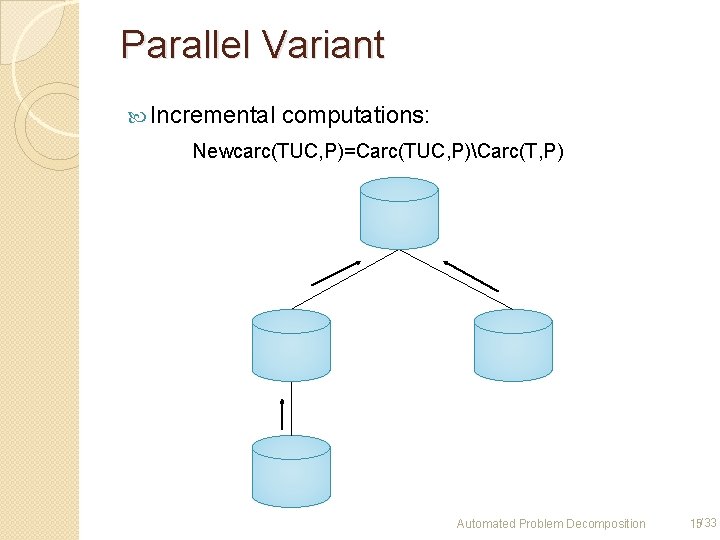
Parallel Variant Incremental computations: Newcarc(TUC, P)=Carc(TUC, P)Carc(T, P) Newcarc Carc Automated Problem Decomposition 15/33

Overview Reasoning task Partition-based algorithm Automated decomposition Experimental evaluation Conclusion Automated Problem Decomposition 16/33

Decomposition of clausal theories Given a Clausal Theory T Find a set of partitions Ti, such that ◦ UTi=T ◦ Reasoning is easier ie the application of partition-based algorithm to this decomposition is as efficient as possible. Minimize the size of the communication languages Ensure that some simplification can be done locally Partitions should be cohesive and loosely coupled. Automated Problem Decomposition 17/33
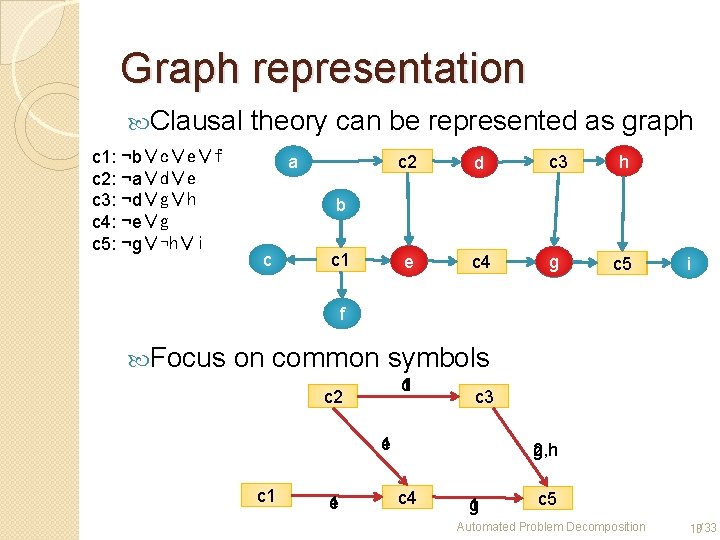
Graph representation Clausal c 1: ¬b∨c∨e∨f c 2: ¬a∨d∨e c 3: ¬d∨g∨h c 4: ¬e∨g c 5: ¬g∨¬h∨i theory can be represented as graph a c 2 d c 3 h e c 4 g c 5 b c c 1 i f Focus on common symbols d 1 c 2 c 3 e 1 c 1 e 1 2 g, h c 4 g 1 c 5 Automated Problem Decomposition 18/33
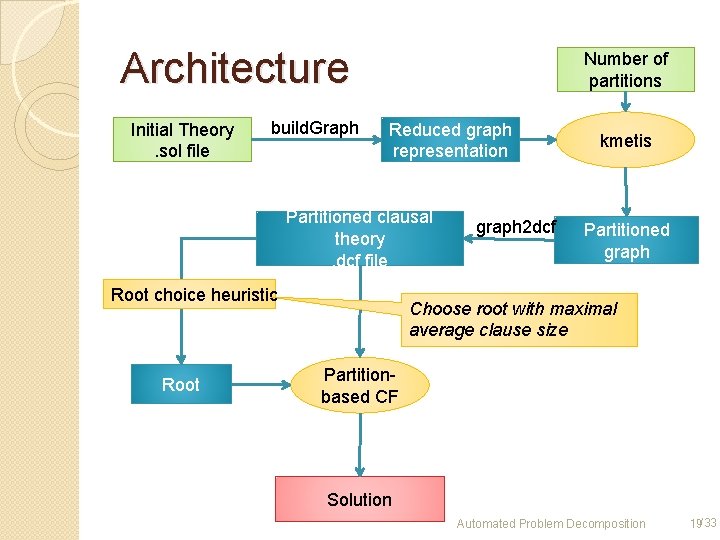
Architecture Initial Theory. sol file build. Graph Number of partitions Reduced graph representation Partitioned clausal theory. dcf file Root choice heuristic Root graph 2 dcf kmetis Partitioned graph Choose root with maximal average clause size Partitionbased CF Solution Automated Problem Decomposition 19/33
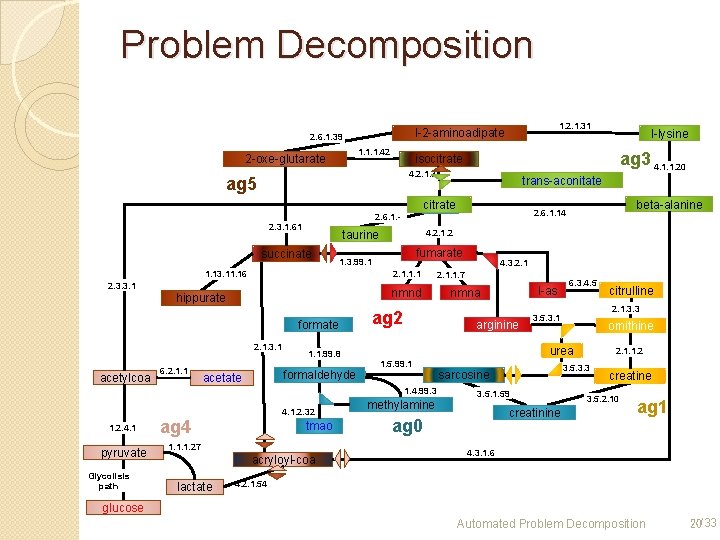
Problem Decomposition 1. 1. 1. 42 2 -oxe-glutarate 1. 2. 1. 31 l-2 -aminoadipate 2. 6. 1. 39 ag 3 4. 1. 1. 20 isocitrate 4. 2. 1. 3 ag 5 trans-aconitate citrate 2. 1. 1. 1 2. 3. 3. 1 nmnd hippurate formate 2. 1. 3. 1 6. 2. 1. 1 fumarate Fumarate 1. 3. 99. 1 1. 13. 11. 16 acetylcoa 4. 2. 1. 2 taurine succinate 1. 1. 99. 8 ag 2 1. 2. 4. 1 pyruvate Glycolisis path ag 4 tmao 1. 1. 1. 27 acryloyl-coa lactate l-as nmna 6. 3. 4. 5 ornithine urea methylamine 3. 5. 1. 59 creatinine ag 0 2. 1. 1. 2 3. 5. 3. 3 sarcosine citrulline 2. 1. 3. 3 3. 5. 3. 1 1. 5. 99. 1 1. 4. 99. 3 4. 1. 2. 32 4. 3. 2. 1. 1. 7 arginine formaldehyde acetate beta-alanine 2. 6. 1. 14 2. 6. 1. - 2. 3. 1. 61 l-lysine creatine 3. 5. 2. 10 ag 1 4. 3. 1. 6 4. 2. 1. 54 glucose Automated Problem Decomposition 20/33

Overview Reasoning task Partition-based algorithm Automated decomposition Experimental evaluation Conclusion Automated Problem Decomposition 21/33

Benchmark Problems Biological networks TPTP problems ◦ Production field : Vocabulary of conjecture (+ removing conjecture) Full vocabulary with length limit SAT problems ◦ Production field Based on frequency of literals N% most/less frequent literals ◦ Size Problems still not tractable as CF problems Solving only a cohesive sub-problem (obtained by partition of the clause graph) Automated Problem Decomposition 22/33
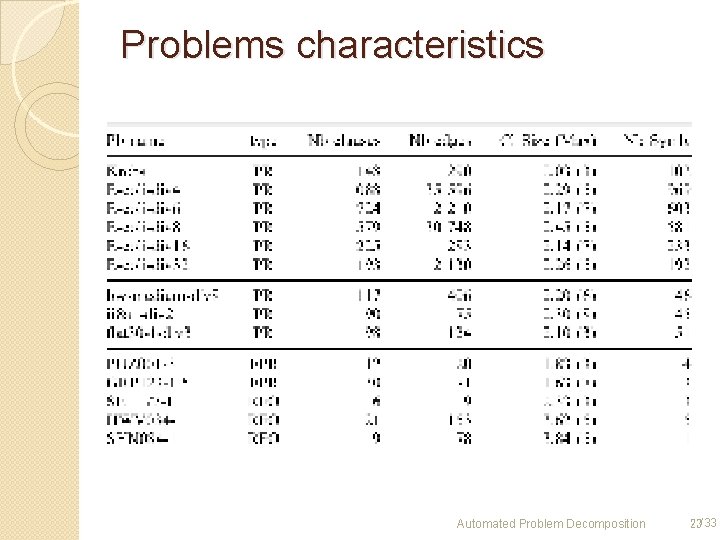
Problems characteristics Automated Problem Decomposition 23/33
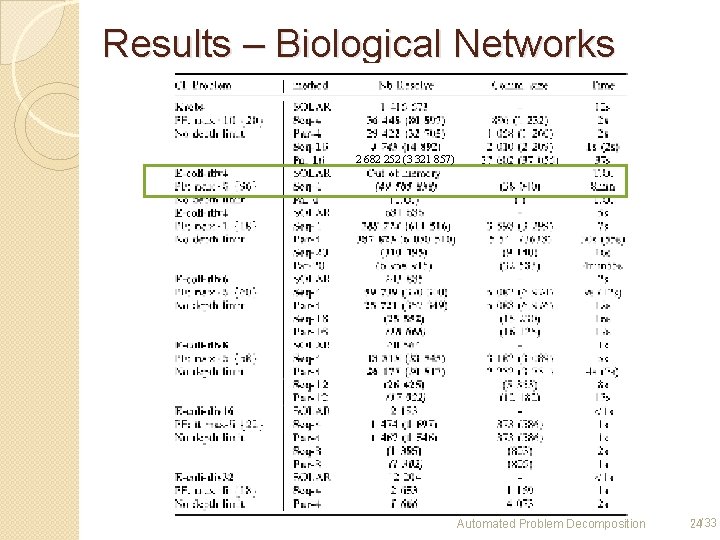
Results – Biological Networks 2 682 252 (3 321 857) Automated Problem Decomposition 24/33
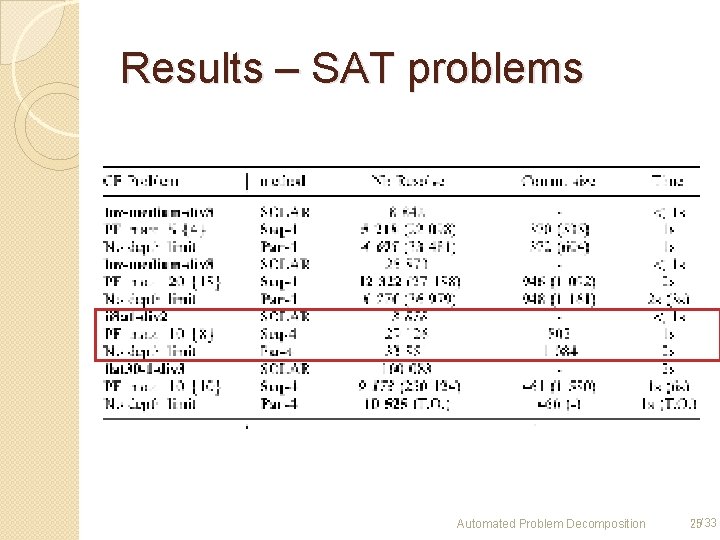
Results – SAT problems Automated Problem Decomposition 25/33
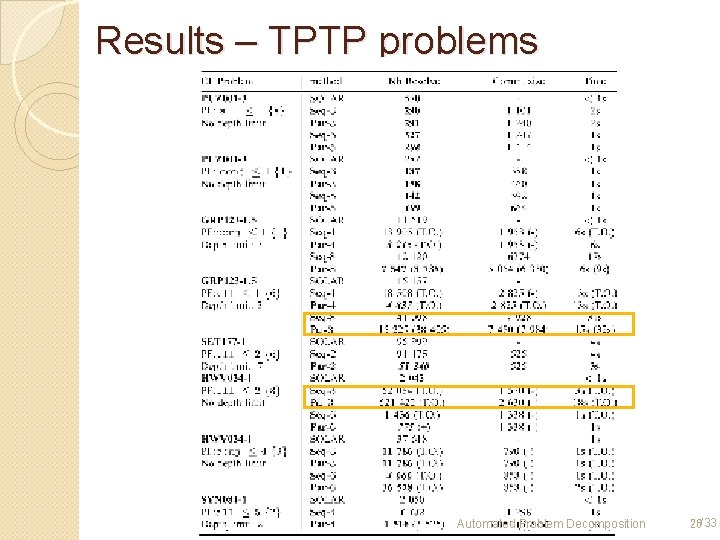
Results – TPTP problems Automated Problem Decomposition 26/33
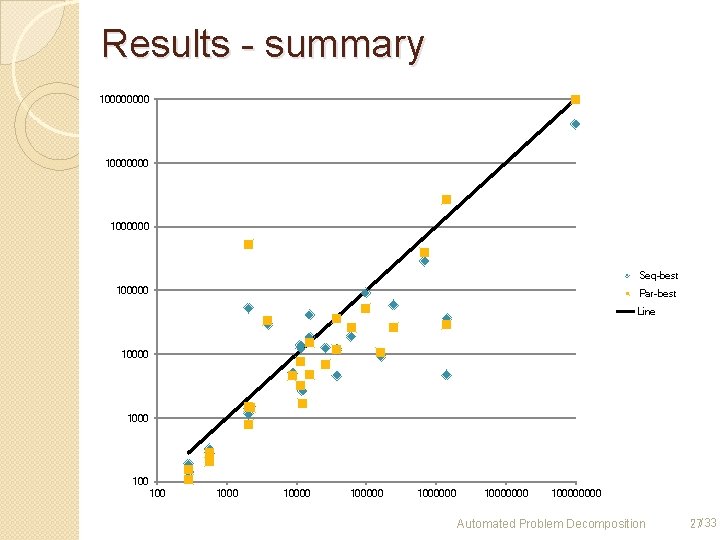
Results - summary 10000000 1000000 Seq-best 100000 Par-best Line 10000 100 100000 10000000 10000 Automated Problem Decomposition 27/33
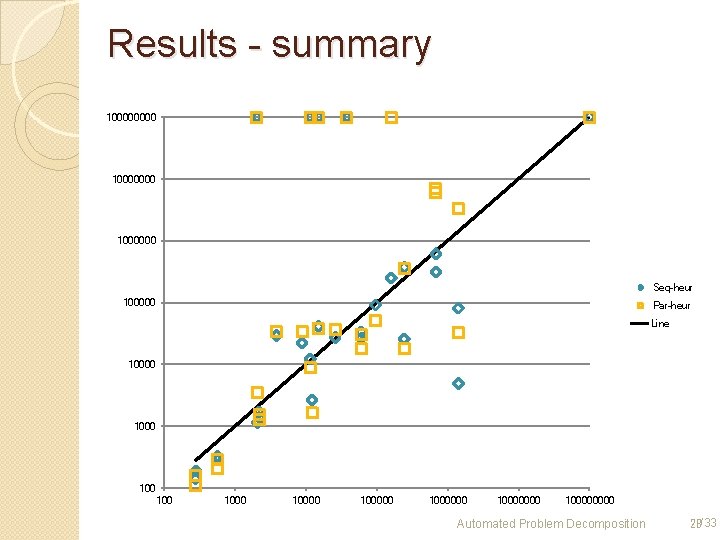
Results - summary 10000000 1000000 Seq-heur 100000 Par-heur Line 10000 100 100000 10000000 10000 Automated Problem Decomposition 28/33

Results For almost all problems, decomposition can reduce the number of resolve operations needed. Especially, it can solve some problems that could not be solved Time is no often improved ◦ Due to communication time (parsing, and such) Approached decomposition with metis: ok. Root choice heuristic: still insufficient, though not bad for biological networks Automated Problem Decomposition 29/33

Overview Reasoning task Partition-based algorithm Automated decomposition Experimental evaluation Conclusion Automated Problem Decomposition 30/33

Conclusion A sound and complete algorithm combined with automated problem decomposition ◦ Can increase efficiency (nb of operation) for almost all problems ◦ But, results dependent on the choice of root Automated Problem Decomposition 31/33

Future works Partition-based algorithm ◦ Variant for Newcarc computations ◦ Common Theories for 1 st order representations ◦ Ordered partitions to break cycle (without removing links) Decomposition ◦ Directly from metabolic pathway ◦ Root choice heuristic Learning preference relation on root choice ◦ Choosing the number of partition Automated Problem Decomposition 32/33

Thank you for your attention Any question ? Automated Problem Decomposition /33
- Slides: 33