Decoding Part II Bhiksha Raj and Rita Singh

Decoding Part II Bhiksha Raj and Rita Singh 19 March 2009 decoding: advanced

Recap and Lookahead o Covered so far: n n n n o String Matching based Recognition Introduction to HMMs Recognizing Isolated Words Learning word models from continuous recordings Building word models from phoneme models Context-independent and context-dependent models Building decision trees Tied-state models Decoding: Concepts Exercise: Training phoneme models Training context-dependent models Building decision trees Training tied-state models Decoding: Practical issues and other topics 19 March 2009 decoding: advanced
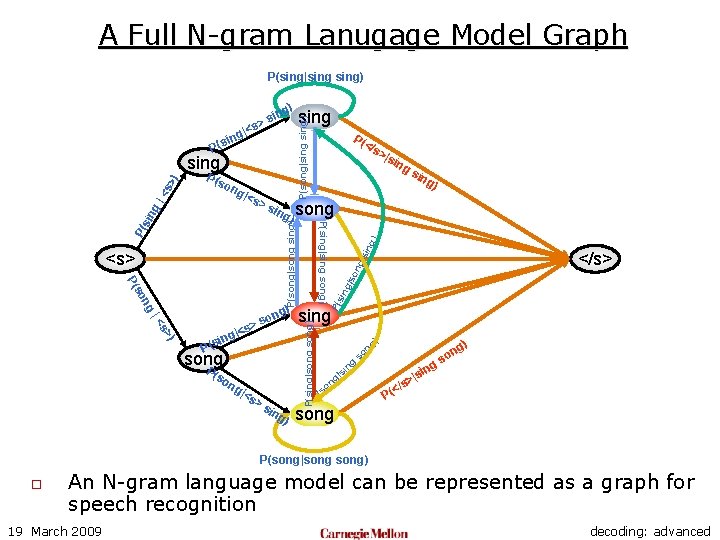
A Full N-gram Lanugage Model Graph P(sing|sing) ) >s ) s> P song ng |<s sin g) >s ing ) ) ing </s> sing P(sing|song) |< s g|< n i s ( so ing ng s P( ng so P( g) on >s P(sing|sing song) <s> P( >|s ing song ) P(song|song sing) |<s </s ng |so ng P( P(s i P(s o sin g| <s >) sing P(song|sing) ng i P(s g sin > |<s g) ng o gs si g| s P( on ) ng n so n |si > /s < P( song P(song|song) o An N-gram language model can be represented as a graph for speech recognition 19 March 2009 decoding: advanced

Generic N-gram representations o o A full N-gram graph can get very large A trigram decoding structure for a vocabulary of D words needs D word instances at the first level and D 2 word instances at the second level n o An N-gram decoding structure will need n o D + D 2 +D 3… DN-1 word instances A simple trigram LM for a vocabulary of 100, 000 words would have… n o Total of D(D+1) word models must be instantiated 100, 000 words is a reasonable vocabulary for a large-vocabulary speech recognition system … an indecent number of nodes in the graph and an obscene number of edges 19 March 2009 decoding: advanced

Lack of Data to the Rescue! o o We never have enough data to learn all D 3 trigram probabilities We learn a very small fraction of these probabilities n Broadcast news: Vocabulary size 64000, training text 200 million words o 10 million trigrams, 3 million bigrams! o All other probabilities are obtained through backoff o This can be used to reduce graph size n o If a trigram probability is obtained by backing off to a bigram, we can simply reuse bigram portions of the graph Thank you Mr. Zipf !! 19 March 2009 decoding: advanced
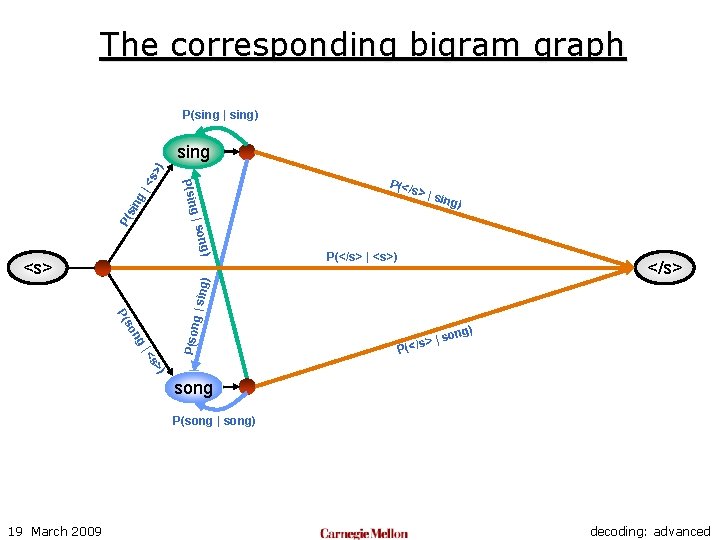
The corresponding bigram graph P(sing | sing) sin g| P(</ s >|s ing) g) | son P( g P(sin <s >) sing P(</s> | <s>) </s> ng |s (</s> ) ong P ) s> |< P(son so P( g | sin g) <s> song P(song | song) 19 March 2009 decoding: advanced
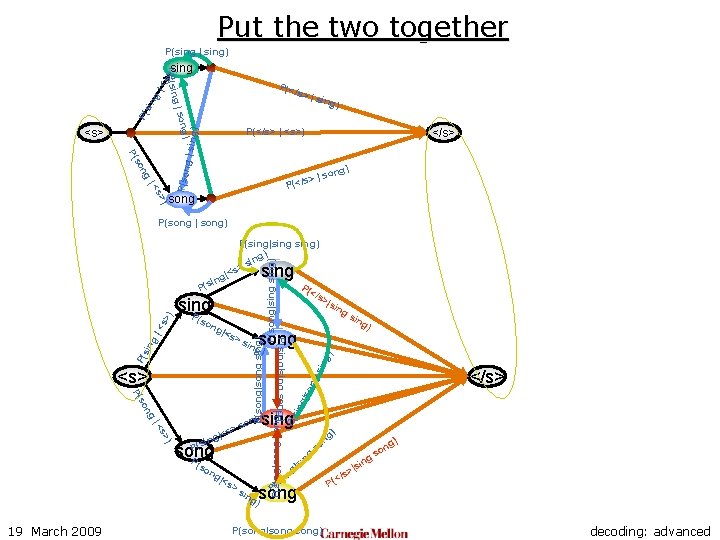
Put the two together P(sing | sing) P(</ s> | P( sin ong) g|s g| <s P(sin >) sing ) P(</s> | <s>) </s> ) song ) s> |< song s> | / < ( P P(son ng so P( g | sin g) <s> sing P(song | song) P(song|song sing) P(song|sing) P(sing|song) P(sing|sing) g) sin > |<s ng i s P( P( </s ng so P( ) s> |< |<s ing P(s song P (so ng 19 March 2009 |<s >s g) sing g) on >s g) ng n so si | ng so P( song ) ing </s> ng P( <s> g) song >s ing ) P(sing|sing song) |<s sin |so ng ing (so >|s P(s sing P sin g |< s> ) sing P(song|song) ) ng n |si s> (</ o gs P decoding: advanced

Using Backoffs o The complete trigram LM for the two word language has the following set of probabilities: n n n 19 March 2009 P(sing P(sing P(song P(song |<s> song) | <s> sing) | sing song) | song sing) | song) decoding: advanced

Using Backoffs o The complete trigram LM for the two word language has the following set of probabilities: n n n 19 March 2009 P(sing P(sing P(song P(song |<s> song) | <s> sing) | sing song) | song sing) | song) o Several of these are not available and obtained by backoff n n P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) decoding: advanced
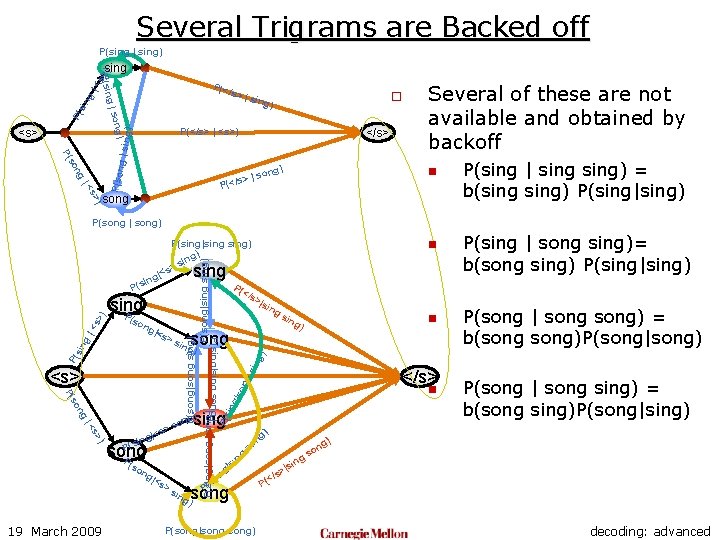
Several Trigrams are Backed off P(sing | sing) P(</ s> | P( | son sin g| <s g P(sin >) sing ) P(</s> | <s>) </s> s> P(</ | son g) Several of these are not available and obtained by backoff n song P(sing | sing) = b(sing) P(sing|sing) ) s> |< P(son ng so P( g | sin g) g) <s> o sing P(song | song) n P(song|song sing) P(song|sing) P(sing|song) P(sing|sing) g) sin > |<s ng i s P( P( </s ng so P( ) s> |< |<s ing P(s song P ng |<s >s n g) ng n so song ) ing P(song|song) ng o gs si | ng so P( P(song | song) = b(song)P(song|song) g) </s> sing g) on s > (so 19 March 2009 ) sin <s> song ing n g) ng P( >s P(sing|sing song) |<s sin |so ng ing P(s (so >|s ing sing P sin g |< s> ) sing P(sing | song sing)= b(song sing) P(sing|sing) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
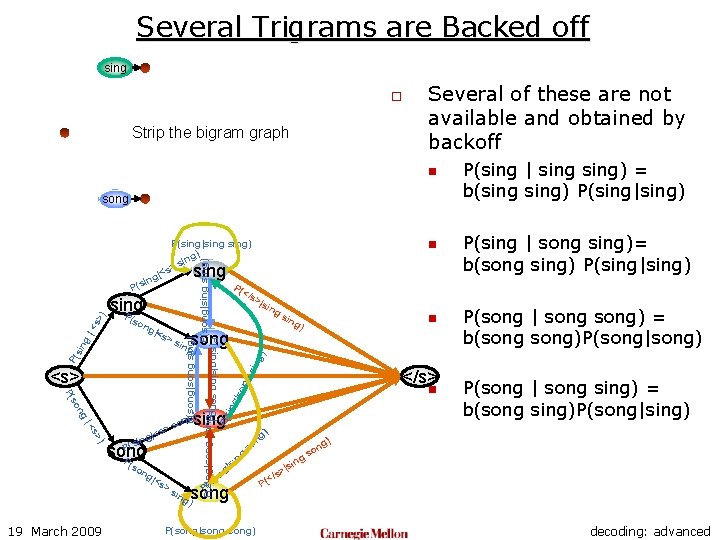
Several Trigrams are Backed off sing o Strip the bigram graph Several of these are not available and obtained by backoff n song n P(song|song sing) P(song|sing) P(sing|song) P(sing|sing) g) sin > |<s ng i s P( P( </s ng so P( ) s> |< |<s ing P(s song P ng |<s >s n g) ng n so song ) ing P(song|song) ng o gs si | ng so P( P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) g) </s> sing g) on s > (so 19 March 2009 ) sin <s> song ing n g) ng P( >s P(sing|sing song) |<s sin |so ng ing P(s (so >|s ing sing P sin g |< s> ) sing P(sing | sing) = b(sing) P(sing|sing) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
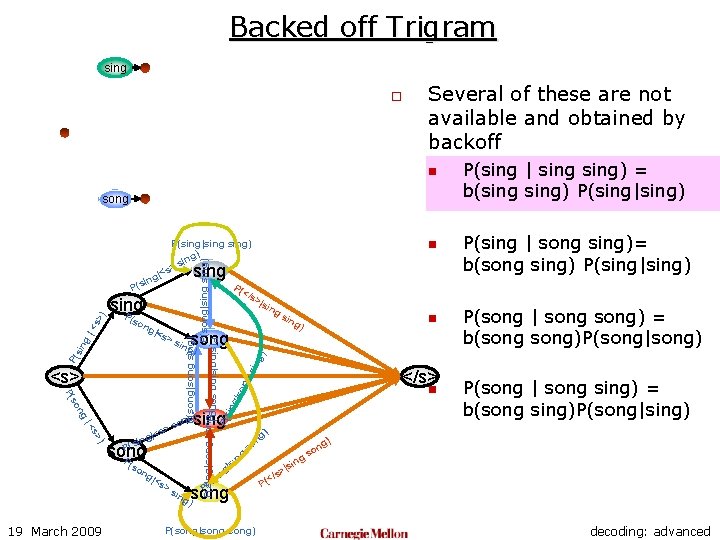
Backed off Trigram sing o Several of these are not available and obtained by backoff n song n P(song|song sing) P(song|sing) P(sing|song) P(sing|sing) g) sin > |<s ng i s P( P( </s ng so P( ) s> |< |<s ing P(s song P ng |<s >s n g) ng n so song ) ing P(song|song) ng o gs si | ng so P( P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) g) </s> sing g) on s > (so 19 March 2009 ) sin <s> song ing n g) ng P( >s P(sing|sing song) |<s sin |so ng ing P(s (so >|s ing sing P sin g |< s> ) sing P(sing | sing) = b(sing) P(sing|sing) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
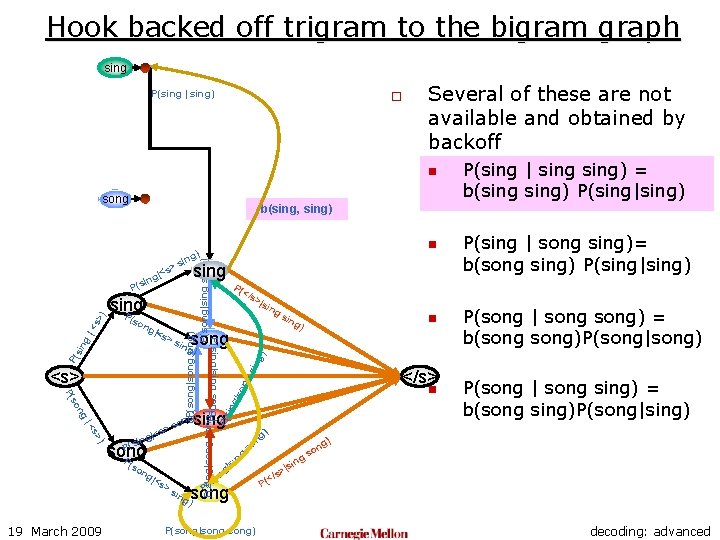
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) ng so P( ) s> |< P(s song P (so ng |<s >s n sing g) ng n so song ) ing P(song|song) ng o gs si | ng so P( P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) g) sin </s> ng ) n g) song ing g) on s > |<s ing sin |so <s> ing P(s P( >s >|s P(sing|sing song) |<s P( </s ing sing P sin g |< s> ) P( ng P(song|song sing) P(song|sing) P(sing|song) sing > (so n g) sin s g|< sin 19 March 2009 P(sing | sing) = b(sing) P(sing|sing) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
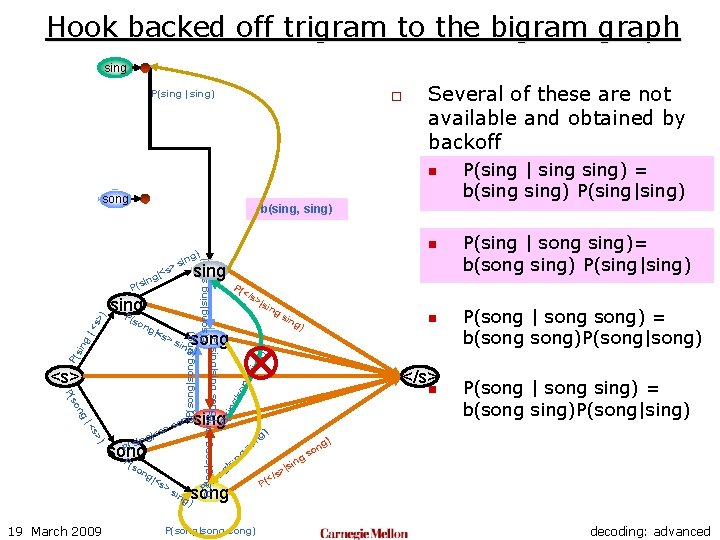
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) ng so P( ) s> |< P(s song P (so ng |<s >s n sing g) ng n so song ) ing P(song|song) ng o gs si | ng so P( P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) g) sin </s> ng ) n g) song ing g) on s > |<s ing sin |so <s> ing P(s P( >s >|s P(sing|sing song) |<s P( </s ing sing P sin g |< s> ) P( ng P(song|song sing) P(song|sing) P(sing|song) sing > (so n g) sin s g|< sin 19 March 2009 P(sing | sing) = b(sing) P(sing|sing) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
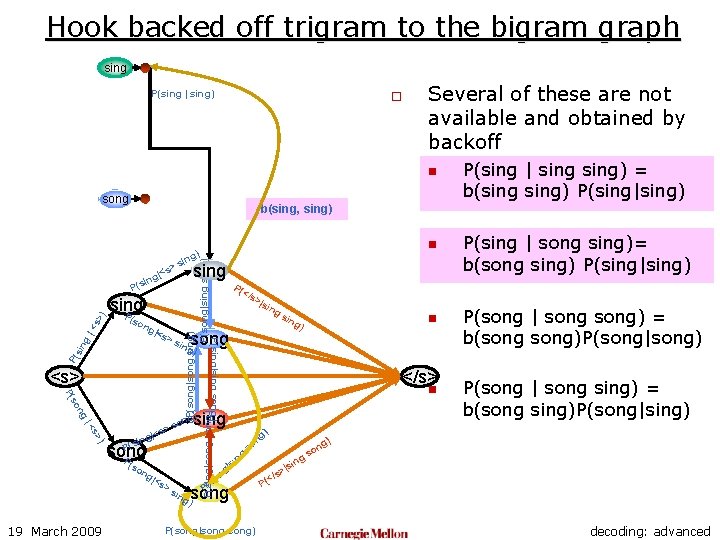
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) sing P |<s P( >s <s> ng so P( ) s> |< P(s song P (so ng |<s >s >|s ing sin ) </s> n sing g) ng n so P( song ) P(song|song) ng o gs si | ng so ing n g) song ing g) on s > |<s ing P( </s P(sing|sing song) sin g |< s> ) P( ng P(song|song sing) P(song|sing) P(sing|song) sing > (so n g) sin s g|< sin 19 March 2009 P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
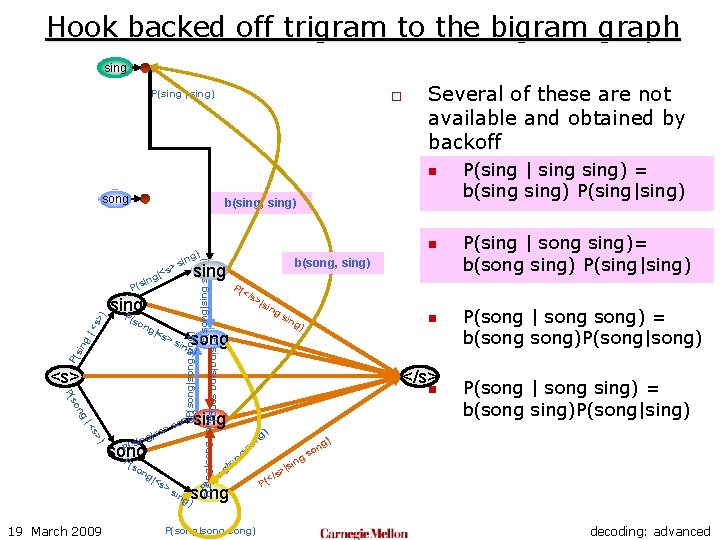
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) P( >s <s> ng so P( ) s> |< P(s song P (so ng 19 March 2009 |<s >s >|s ing sin ) </s> n sing g) ng n so P( song ) P(song|song) ng o gs si | ng so ing n g) song ing g) on s > |<s ing P( </s P(sing|sing song) |<s P(song|song sing) P(song|sing) P(sing|song) sing P sin g |< s> ) P(s ng b(song, sing) sing > |<s ing (so n g) sin P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
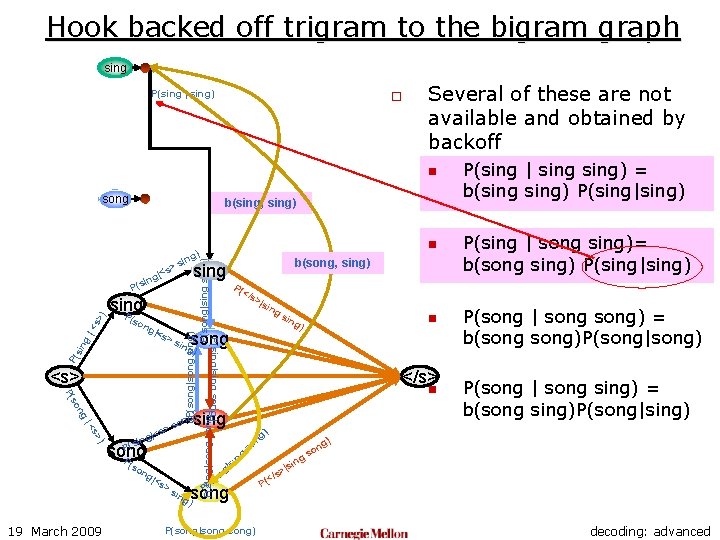
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) P( >s <s> ng so P( ) s> |< P(s song P (so ng 19 March 2009 |<s >s >|s ing sin ) </s> n sing g) ng n so P( song ) P(song|song) ng o gs si | ng so ing n g) song ing g) on s > |<s ing P( </s P(sing|sing song) |<s P(song|song sing) P(song|sing) P(sing|song) sing P sin g |< s> ) P(s ng b(song, sing) sing > |<s ing (so n g) sin P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
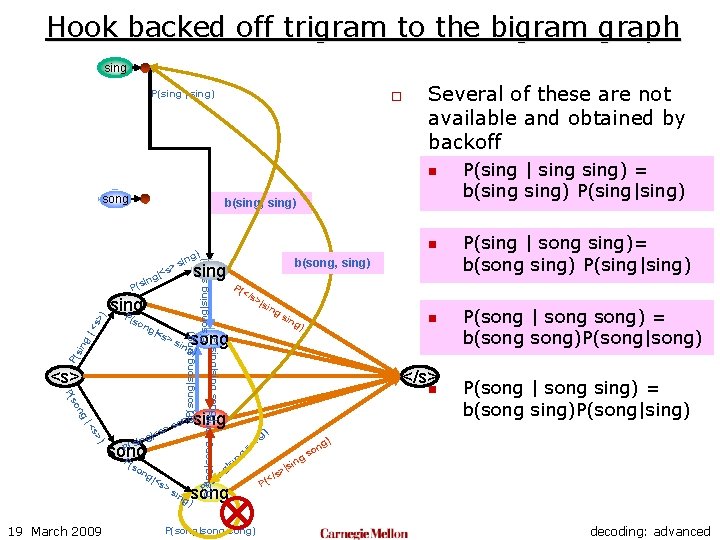
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) P( >s <s> ng so P( ) s> |< P(s song P (so ng 19 March 2009 |<s >s >|s ing sin ) </s> n sing g) ng n so P( song ) P(song|song) ng o gs si | ng so ing n g) song ing g) on s > |<s ing P( </s P(sing|sing song) |<s P(song|song sing) P(song|sing) P(sing|song) sing P sin g |< s> ) P(s ng b(song, sing) sing > |<s ing (so n g) sin P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
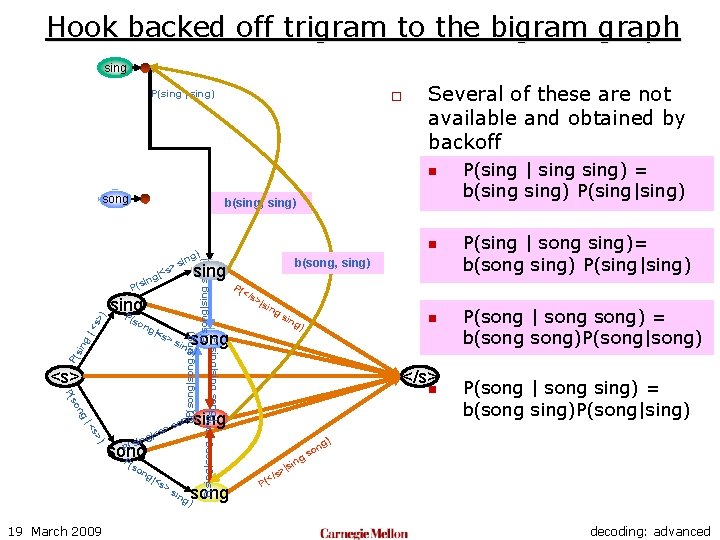
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) P( >s <s> ng so P( ) s> |< s P( song P (so ng 19 March 2009 |<s >s >|s ing sin ) n g) song ing </s> n sing g) on s > |<s ing P( </s P(sing|sing song) |<s P(song|song sing) P(song|sing) P(sing|song) sing P sin g |< s> ) P(s ng b(song, sing) sing > |<s ing (so n g) sin song ) ing ng o gs P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) ) n |si s> (</ P decoding: advanced
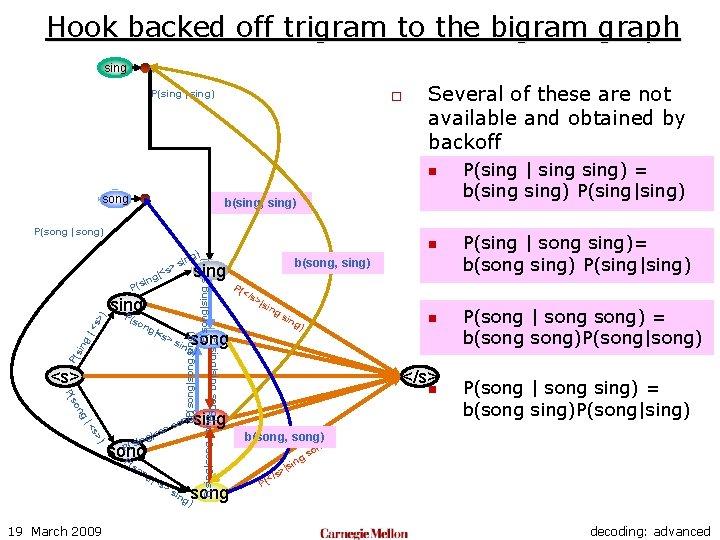
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) P(song | song) P( >s <s> ng so P( ) s> |< P(s P( so song ng 19 March 2009 |<s >s >|s ing sin ) n g) song ing </s> n sing g) on s > |<s ing P( </s P(sing|sing song) |<s P(song|song sing) P(song|sing) P(sing|song) sing P sin g |< s> ) P(s ng b(song, sing) sing > |<s ing (so n g) sin song ) ing P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) b(song, song) ) ng o gs n |si s> (</ P decoding: advanced
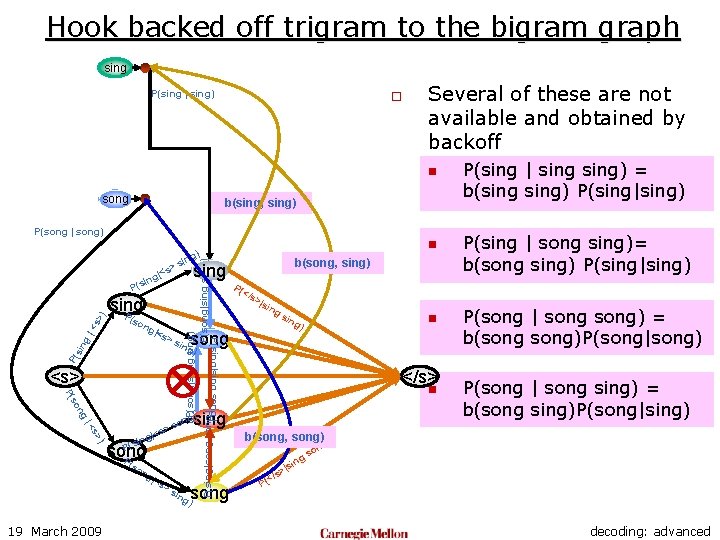
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) P(song | song) P( >s <s> ng so P( ) s> |< P(s P( so song ng 19 March 2009 |<s >s >|s ing sin ) n g) song ing </s> n sing g) on s > |<s ing P( </s P(sing|sing song) |<s P(song|song sing) P(song|sing) P(sing|song) sing P sin g |< s> ) P(s ng b(song, sing) sing > |<s ing (so n g) sin song ) ing P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) b(song, song) ) ng o gs n |si s> (</ P decoding: advanced
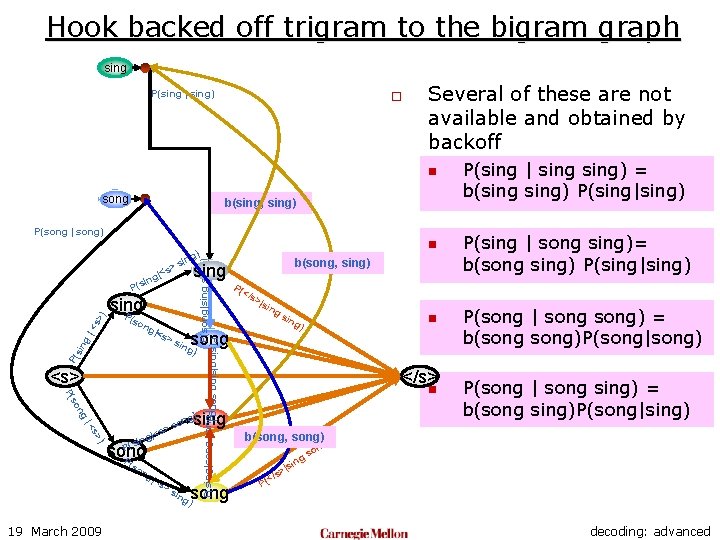
Hook backed off trigram to the bigram graph sing P(sing | sing) o Several of these are not available and obtained by backoff n song b(sing, sing) P(song | song) P(song|sing) sing P P( ing ) <s> ng so P( ) s> |< |<s ing song ng 19 March 2009 |<s >s ing sin n g) </s> n sing g) on s > P(s P( so >|s song >s P(sing|song) |<s P( </s P(sing|sing song) sin g |< s> ) P(s ng b(song, sing) sing > |<s ing (so n g) sin song ) ing P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) b(song, song) ) ng o gs n |si s> (</ P decoding: advanced
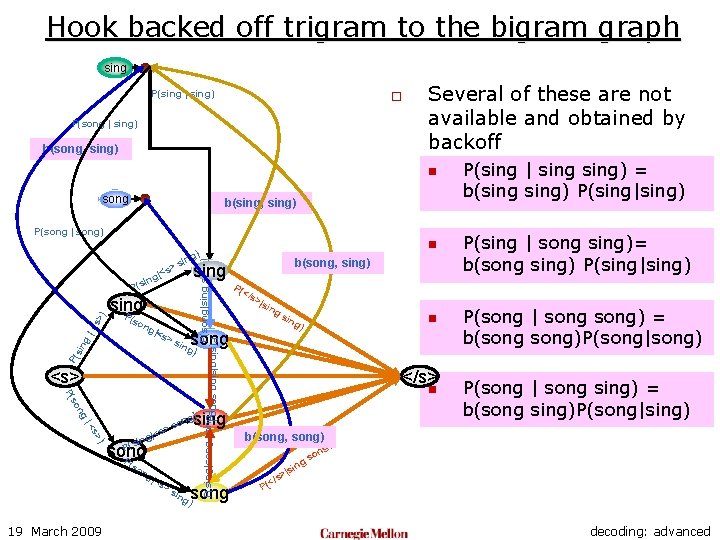
Hook backed off trigram to the bigram graph sing P(sing | sing) o P(song | sing) b(song, sing) Several of these are not available and obtained by backoff n song b(sing, sing) P(song | song) P(song|sing) sing P P( ing ) <s> ng so P( ) s> |< |<s ing song ng 19 March 2009 |<s >s ing sin n g) </s> n sing g) on s > P(s P( so >|s song >s P(sing|song) |<s P( </s P(sing|sing song) sin g |< s> ) P(s ng b(song, sing) sing > |<s ing (so n g) sin song ) ing P(sing | sing) = b(sing) P(sing|sing) P(sing | song sing)= b(song sing) P(sing|sing) P(song | song) = b(song)P(song|song) P(song | song sing) = b(song sing)P(song|sing) b(song, song) ing n so g) |s /s> < P( decoding: advanced
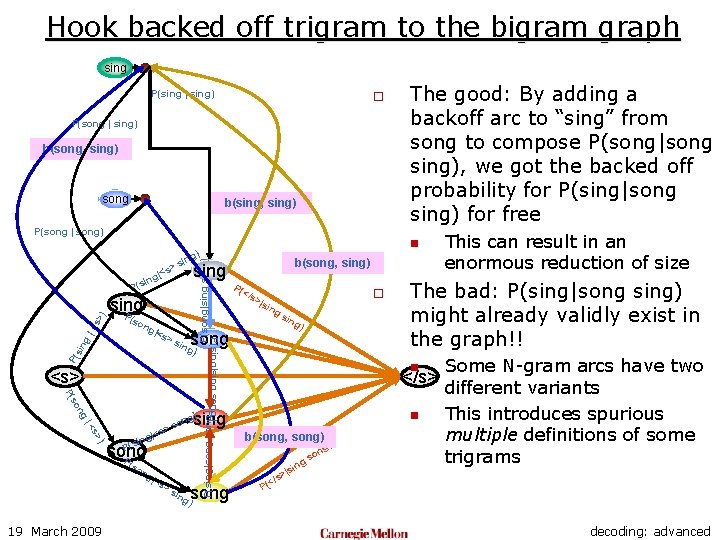
Hook backed off trigram to the bigram graph sing P(sing | sing) o P(song | sing) b(song, sing) song b(sing, sing) P(song | song) sin g P( ing ) <s> ng so P( ) s> |< song P (so 19 March 2009 |<s >s ing sin g) n n song ) ing b(song, song) ing |s /s> n so g) This can result in an enormous reduction of size The bad: P(sing|song sing) might already validly exist in the graph!! </s> sing g) on s > s g|< ng o >|s song >s in P(s P( </s P(sing|sing song) |<s P(sing|song) ) s> sing P ng b(song, sing) sing P(s |< P(song|sing) >s (so n ) ing |<s ing The good: By adding a backoff arc to “sing” from song to compose P(song|song sing), we got the backed off probability for P(sing|song sing) for free Some N-gram arcs have two different variants This introduces spurious multiple definitions of some trigrams < P( decoding: advanced

Even compressed graphs are large o Even a compressed N-gram word graph can get very large n n o Explicit arcs for at least every bigram and every trigram in the LM This can get to tens or hundreds of millions Approximate structures required n n The approximate structure is, well, approximate It reduces the graph size o o 19 March 2009 This breaks the requirement that every node in the graph represents a unique word history We compensate by using additional external structures to track word history decoding: advanced
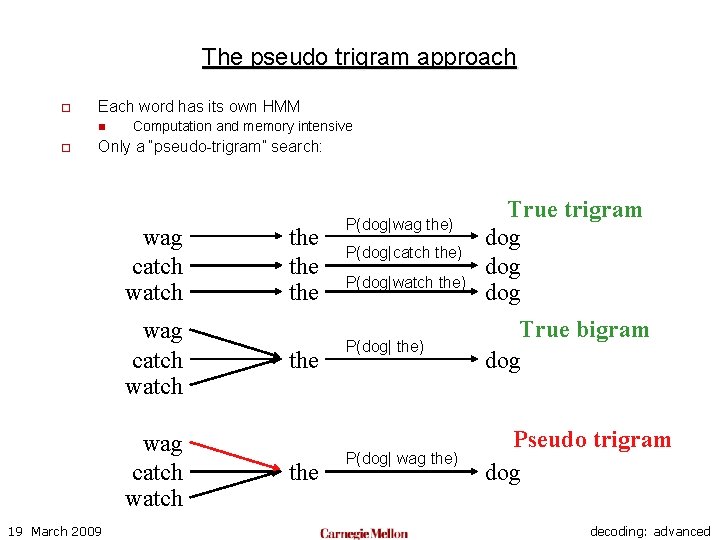
The pseudo trigram approach o Each word has its own HMM n o Computation and memory intensive Only a “pseudo-trigram” search: wag catch watch 19 March 2009 the the the P(dog|wag the) P(dog|catch the) P(dog|watch the) True trigram dog dog P(dog| the) True bigram dog P(dog| wag the) Pseudo trigram dog decoding: advanced
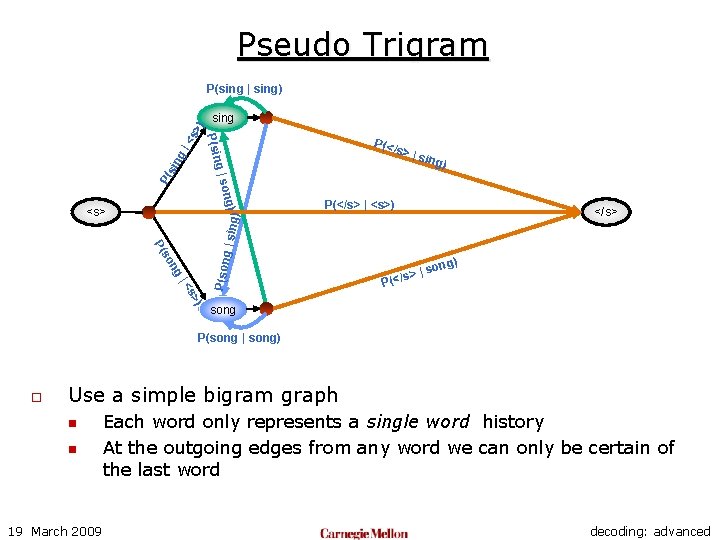
Pseudo Trigram P(</ s >|s ing) P( g|s sin g| sing P(sin <s >) P(sing | sing) ong) P(</s> | <s>) </s> ng P(son so P( g | sin g) <s> ) s> |< |s (</s> ) ong P song P(song | song) o Use a simple bigram graph n n 19 March 2009 Each word only represents a single word history At the outgoing edges from any word we can only be certain of the last word decoding: advanced
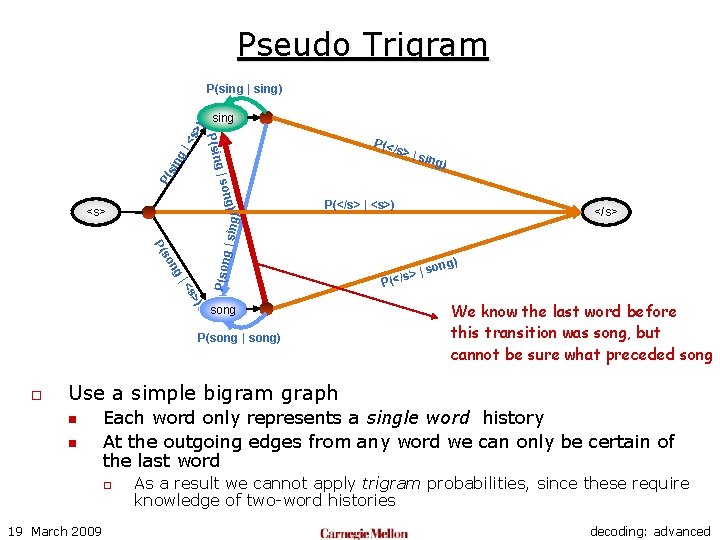
Pseudo Trigram P(</ s >|s ing) P( g|s sin g| sing P(sin <s >) P(sing | sing) ong) P(</s> | <s>) g | sin ng P(son so P( ) s> |< song P(song | song) o </s> g) <s> |s (</s> ) ong P We know the last word before this transition was song, but cannot be sure what preceded song Use a simple bigram graph n n Each word only represents a single word history At the outgoing edges from any word we can only be certain of the last word o 19 March 2009 As a result we cannot apply trigram probabilities, since these require knowledge of two-word histories decoding: advanced
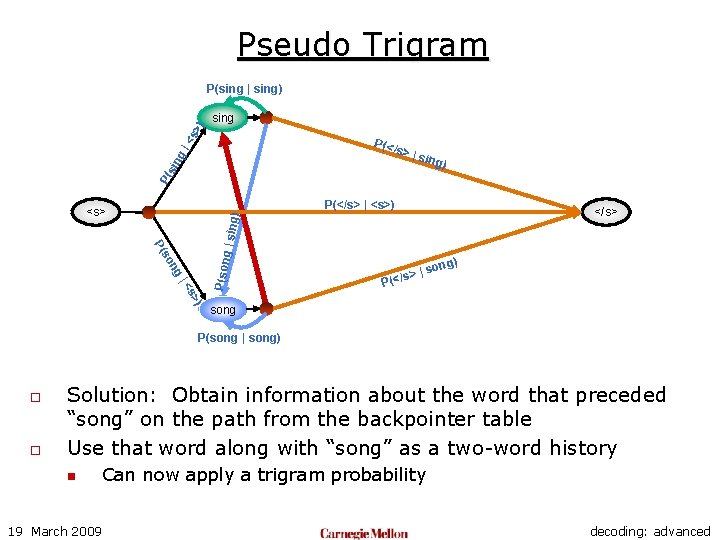
Pseudo Trigram sing <s >) P(sing | sing) P(</ s P( sin g| >|s ing) P(</s> | <s>) </s> ng P(son so P( g | sin g) <s> ) s> |< |s (</s> ) ong P song P(song | song) o o Solution: Obtain information about the word that preceded “song” on the path from the backpointer table Use that word along with “song” as a two-word history n Can now apply a trigram probability 19 March 2009 decoding: advanced

Pseudo Trigram o The problem with the pseudo-trigram approach is that the LM probabilities to be applied can no longer be stored on the graph edge n n o As a result, the recognition output obtained from the structure is no longer guaranteed optimal in a Bayesian sense! Nevertheless the results are fairly close to optimal n o The actual probability to be applied will differ according to the best previous word obtained from the backpointer table The loss in optimality due to the reduced dynamic structure is acceptable, given the reduction in graph size This form of decoding is performed in the “fwdflat” mode of the sphinx 3 decoder 19 March 2009 decoding: advanced

Pseudo Trigram: Still not efficient o Even a bigram structure can be inefficient to search n n n 19 March 2009 Large number of models Many edges Not taking advantage of shared portions of the graph decoding: advanced
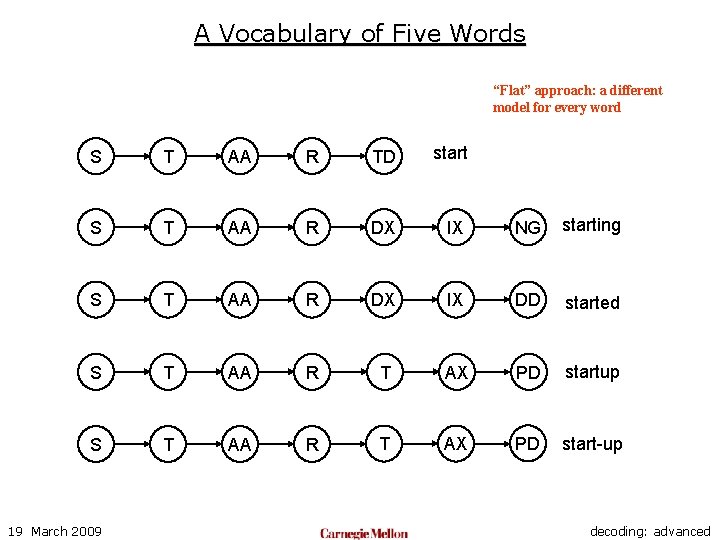
A Vocabulary of Five Words “Flat” approach: a different model for every word S T AA R TD start S T AA R DX IX NG starting S T AA R DX IX DD started S T AA R T AX PD startup S T AA R T AX PD start-up 19 March 2009 decoding: advanced
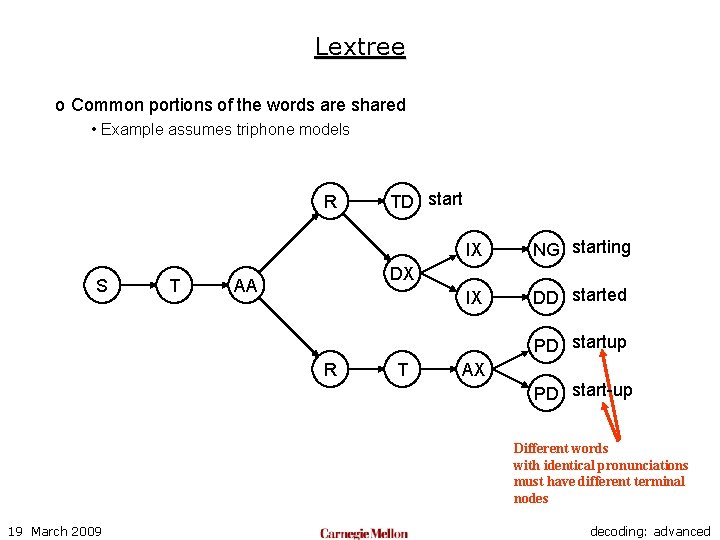
Lextree o Common portions of the words are shared • Example assumes triphone models R S T TD start IX NG starting IX DD started DX AA PD startup R T AX PD start-up Different words with identical pronunciations must have different terminal nodes 19 March 2009 decoding: advanced
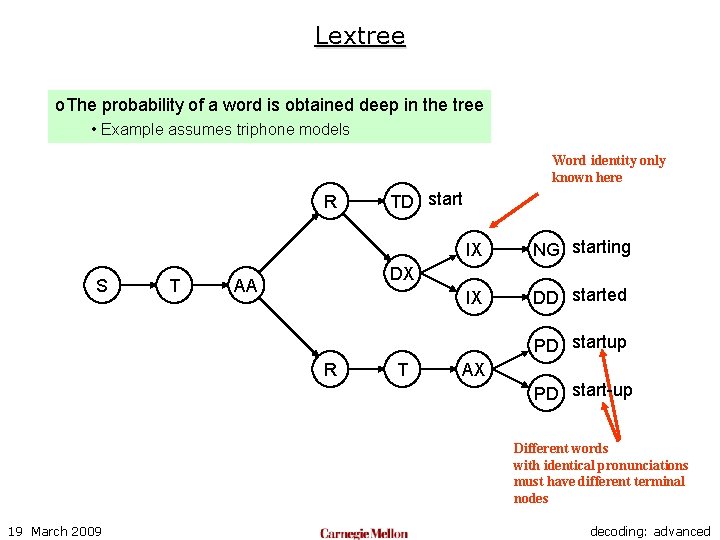
Lextree o. The probability of a word is obtained deep in the tree • Example assumes triphone models Word identity only known here R S T TD start IX NG starting IX DD started DX AA PD startup R T AX PD start-up Different words with identical pronunciations must have different terminal nodes 19 March 2009 decoding: advanced
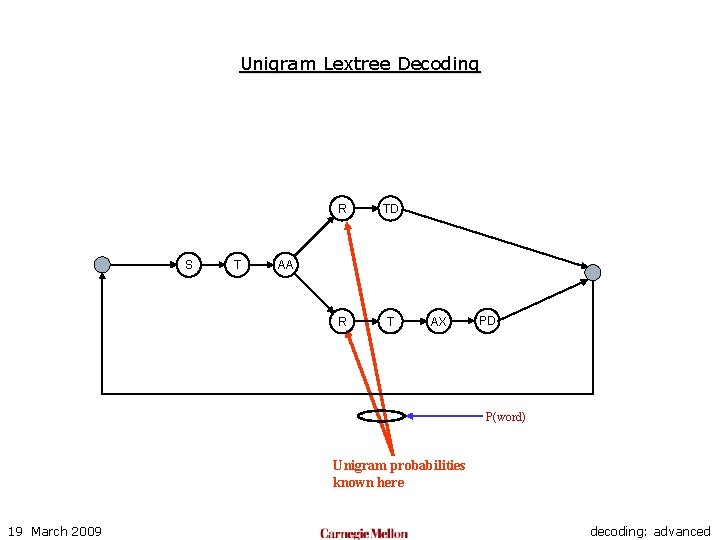
Unigram Lextree Decoding S T R TD R T AA AX PD P(word) Unigram probabilities known here 19 March 2009 decoding: advanced

Lextrees o Superficially, lextrees appear to be highly efficient structures n o A lextree representation of a dictionary of 100000 words typically reduces the overall structure by a factor of 10, as compared to a “flat” representation However, all is not hunky dory. . 19 March 2009 decoding: advanced
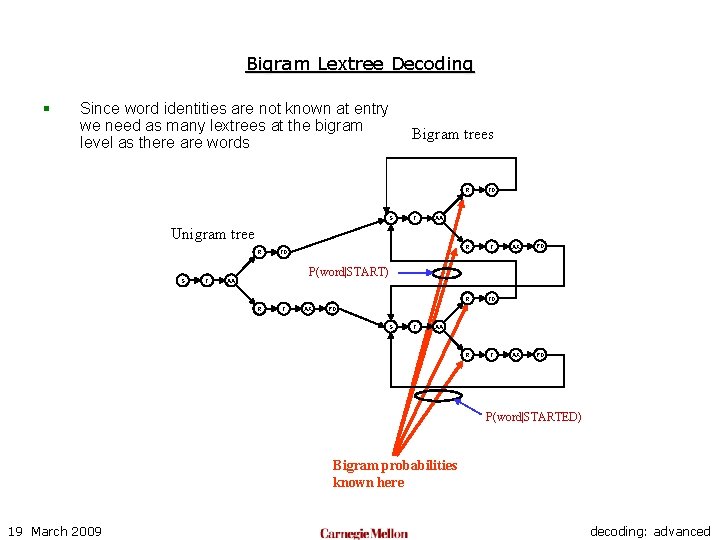
Bigram Lextree Decoding § Since word identities are not known at entry we need as many lextrees at the bigram level as there are words S Bigram trees T R TD R T AA Unigram tree R S T TD AX PD P(word|START) AA R T AX PD S T AA P(word|STARTED) Bigram probabilities known here 19 March 2009 decoding: advanced
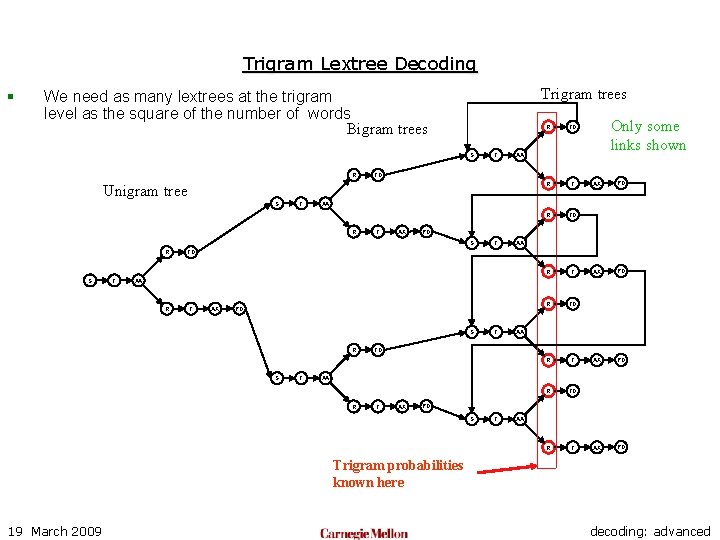
Trigram Lextree Decoding § Trigram trees We need as many lextrees at the trigram level as the square of the number of words Bigram trees S R T T R TD R T TD T AX AX PD PD S S R Only some links shown AA R R TD AA Unigram tree S R T AA TD AA R T AX PD S R S T T AA TD AA R T AX PD S T AA Trigram probabilities known here 19 March 2009 decoding: advanced

Lextrees o o The “ideal” lextree structure is MUCH larger than an ideal “flat” structure As in the case of flat structures, the size of the ideal structure can be greatly reduced by accounting for the fact that most Ngram probabilities are obtained by backing off o Even so the structure can get very large. o Approximate structures are needed. 19 March 2009 decoding: advanced
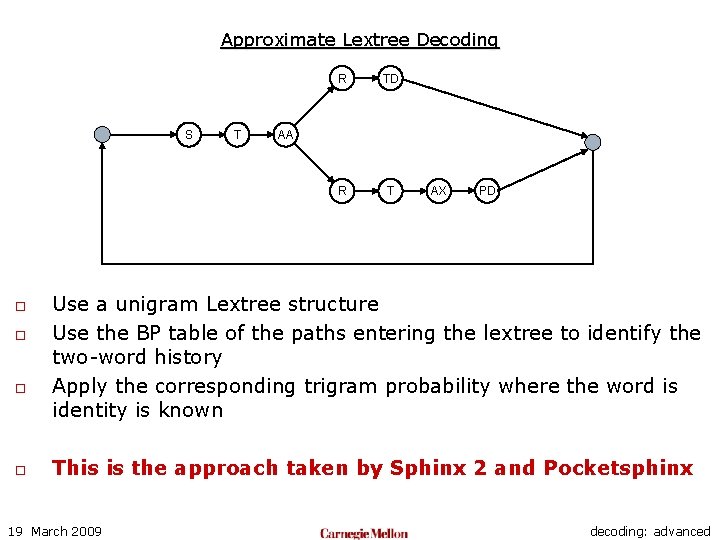
Approximate Lextree Decoding S o o T R TD R T AA AX PD Use a unigram Lextree structure Use the BP table of the paths entering the lextree to identify the two-word history Apply the corresponding trigram probability where the word is identity is known This is the approach taken by Sphinx 2 and Pocketsphinx 19 March 2009 decoding: advanced

Approximate Lextree Decoding o Approximation is far worse than the pseudo-trigram approximation n The basic graph is a unigram graph o o Pseudo-trigram uses a bigram graph! Far more efficient than any structure seen so far n Used for real-time large vocabulary recognition in ’ 95! o How do we retain the efficiency, and yet improve accuracy? o Ans: Use multiple lextrees n 19 March 2009 Still a small number, e. g. 3. decoding: advanced
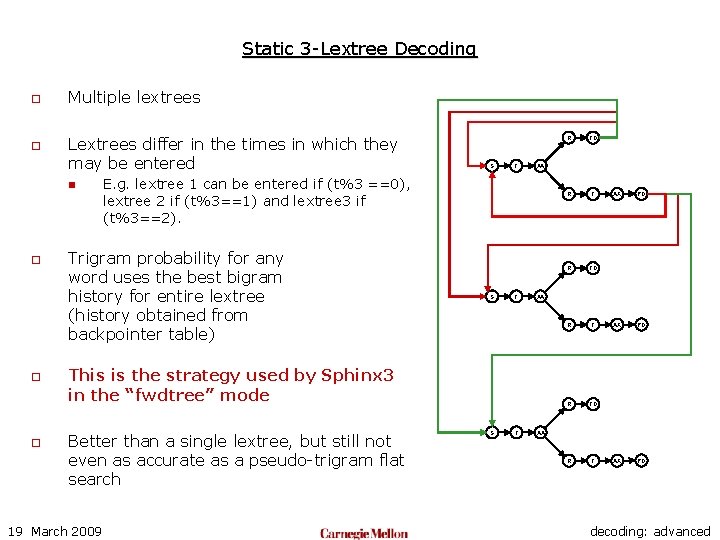
Static 3 -Lextree Decoding o o Multiple lextrees Lextrees differ in the times in which they may be entered n o o o S T 19 March 2009 S T R TD R T AX PD AA This is the strategy used by Sphinx 3 in the “fwdtree” mode Better than a single lextree, but still not even as accurate as a pseudo-trigram flat search TD AA E. g. lextree 1 can be entered if (t%3 ==0), lextree 2 if (t%3==1) and lextree 3 if (t%3==2). Trigram probability for any word uses the best bigram history for entire lextree (history obtained from backpointer table) R AA decoding: advanced

Dynamic Tree Composition o o o Build a “theoretically” correct N-gram lextree However, only build the portions of the lextree that are requried Prune heavily to eliminate unpromising portions of the graphs n o In practice, explicit composition of the lextree dynamically can be very expensive n o To reduce composition and freeing Since portions of the large graph are being continuously constructed and abandoned Need a way to do this virtually -- get the same effect without actually constructing the tree 19 March 2009 decoding: advanced
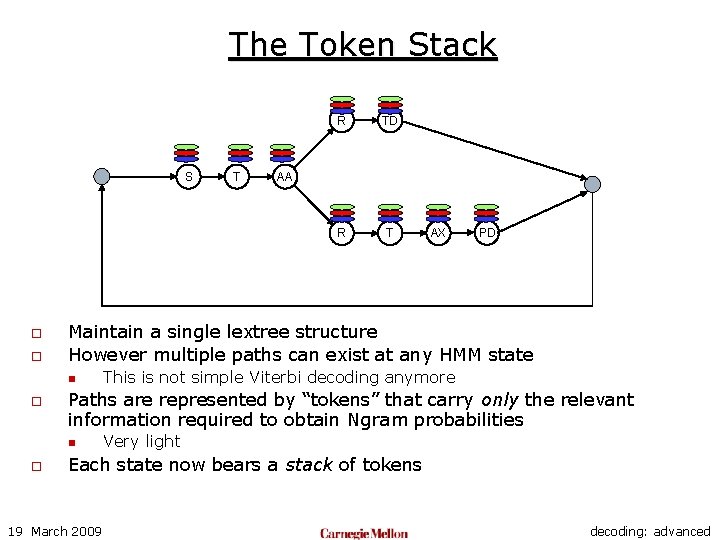
The Token Stack S o o R T AA AX PD This is not simple Viterbi decoding anymore Paths are represented by “tokens” that carry only the relevant information required to obtain Ngram probabilities n o TD Maintain a single lextree structure However multiple paths can exist at any HMM state n o T R Very light Each state now bears a stack of tokens 19 March 2009 decoding: advanced

Token Stack o o The token stack emulates full lextree graphs Efficiency is obtained by restricting the number of active tokens at any state n n If we allow N tokens max at any state, we effectively only need the physical resources equivalent to N lextrees But the tokens themselves represent components of many different N-gram level lextrees o Most optimal of all described approaches o Sphinx 4 takes this approach o Problems: Improper management of token stacks can lead to large portions of the graph representing different variants of the same word sequence hypothesis n 19 March 2009 No net benefit over multiple (N) fixed lextrees decoding: advanced

Which to choose o o Depends on the task and your patience Options n Pocket sphinx/ sphinx 2 : Single lextree o o n Sphinx 3 fwdflat: Bigram graph with backpointer histories o o o n o o Fast Suboptimal Needs tuning Sphinx 4: Token-stack lextree o o o 19 March 2009 Slow Somewhat suboptimal Little tuning Sphinx 3 fwdtree: Multiple lextrees with backpointer histories o n Very fast Little tuning Speed > fwdflat, Speed < fwdtree Potentially optimal But only if very carefully tuned decoding: advanced

Language weights o The Bayesian classification equation for speech recognition is Speech recognition system solves Acoustic model For HMM-based systems this is an HMM 19 March 2009 Lanugage model decoding: advanced

Language weights o The standard Bayesian classification equation attempts to recognize speech for best average sentence recognition error n n o But hidden in it is an assumption: n n n o NOT word recognition error Its defined over sentences The infinity of possible word sequences is the same size as the infinity of possible acoustic realizations of them They are not The two probabilities are not comparable – the acoustic evidence will overwhelm the language evidence Compensating for it: The language weight n To compensate for it, we apply a language weight to the language probabilities o o 19 March 2009 Raise them to a power This increases the relative differences in the probabilities of words decoding: advanced

Language weights o The Bayesian classification equation for speech recognition is modified to lwt o Which is equivalent to o Lwt is the language weight 19 March 2009 decoding: advanced

Language Weights o o o They can be incrementally applied Which is the same as The language weight is applied to each N-gram probability that gets factored in! 19 March 2009 decoding: advanced

Optimizing Language Weight: Example o o No. of active states, and word error rate variation with language weight (20 k word task) Relaxing pruning improves WER at LW=14. 5 to 14. 8% 19 March 2009 decoding: advanced
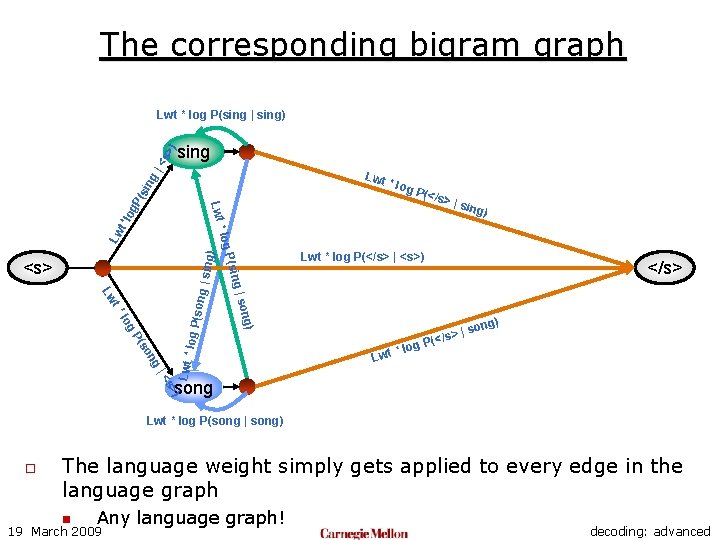
The corresponding bigram graph Lwt * log P(sing | sing) <s >) sing * log *lo g | sing </s> log ng so P( * Lwt |s (</s> log P song s> |< Lwt * ) ong g) (song Lwt * log P(</s> | <s>) | son t* Lw log P g P(sin ) Lw t * log <s> P(</ s> | s ing) Lwt P( sin g| Lwt ) Lwt * log P(song | song) o The language weight simply gets applied to every edge in the language graph n Any 19 March 2009 language graph! decoding: advanced

Language Weights o Language weights are strange beasts n n o Increasing them decreases the a priori probability of any word sequences But it increases the relative differences between the probabilities of word sequences The effect of language weights is not understood n Some claim increasing the language weight increases the contribution of the LM to recognition o o This would be true if only the second point above were true How to set them n n n 19 March 2009 Try a bunch of different settings Whatever works! The optimal setting is recognizer dependent decoding: advanced
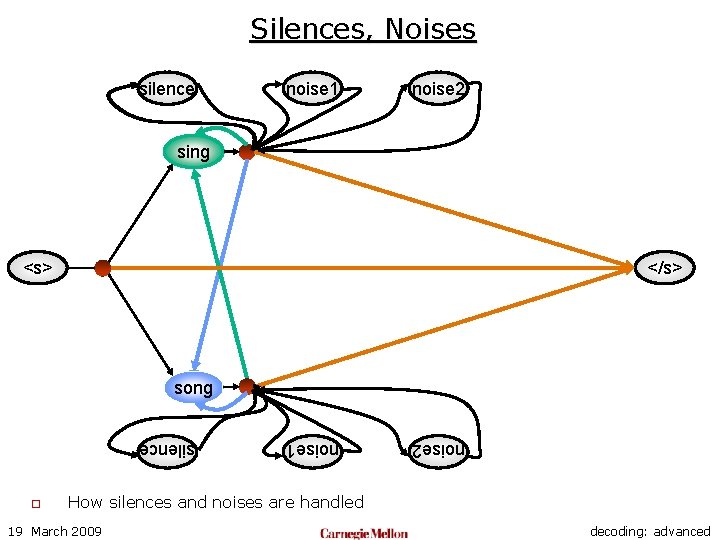
Silences, Noises silence noise 1 noise 2 sing <s> </s> song noise 2 noise 1 silence o How silences and noises are handled 19 March 2009 decoding: advanced

Silences and Noises silence noise 1 noise 2 sing o Silences are given a special probability n n o Called silence penalty Determines the probability that the speaker pauses between words Noises are given a “noise” probability n n 19 March 2009 The probability of the noise occurring between words Each noise may have a different probability decoding: advanced

Silences and Noises silence noise 1 noise 2 sing o Silences are given a special probability n n o Called silence penalty Determines the probability that the speaker pauses between words Noises are given a “noise” probability n n 19 March 2009 The probability of the noise occurring between words Each noise may have a different probability decoding: advanced
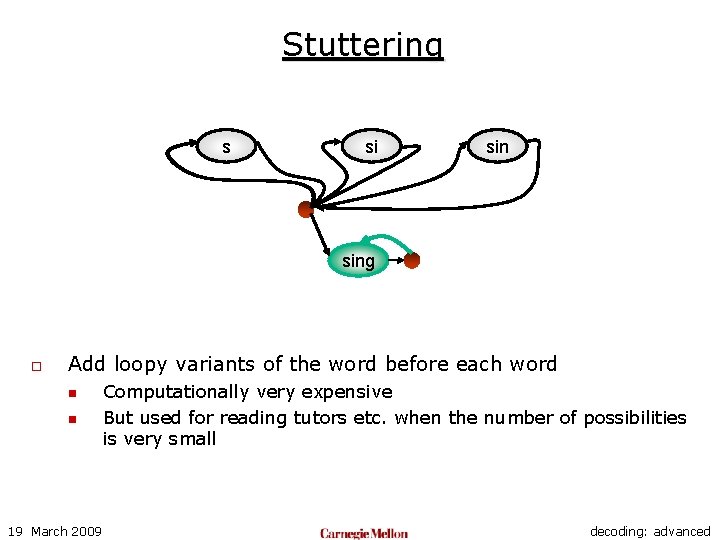
Stuttering silence s noise 1 si noise 2 sing o Add loopy variants of the word before each word n n 19 March 2009 Computationally very expensive But used for reading tutors etc. when the number of possibilities is very small decoding: advanced

Rescoring and N-best Hypotheses o o The tree of words in the backpointer table is often collapsed to a graph called a lattice The lattice is a much smaller graph than the original language graph n o Common technique: n n o Not loopy for one Compute a lattice using a small, crude language model Modify lattice so that the edges on the graph have probabilities derived from a high-accuracy LM Decode using this new graph Called Rescoring An algorithm called A-STAR can be used to derive the N best paths through the graph 19 March 2009 decoding: advanced

Confidence o Skipping this for now 19 March 2009 decoding: advanced
- Slides: 59