Decoding Neural Signals for the Control of Movement

Decoding Neural Signals for the Control of Movement Jim Rebesco and Sara Solla Lee Miller and Nicho Hatsopoulos

Outline • Recording of neural activity in primary motor cortex during task execution. • Analysis of multielectrode data based on directional tuning: linear dimensionality reduction. • Uncovering task-specific low dimensional manifolds: nonlinear dimensionality reduction.

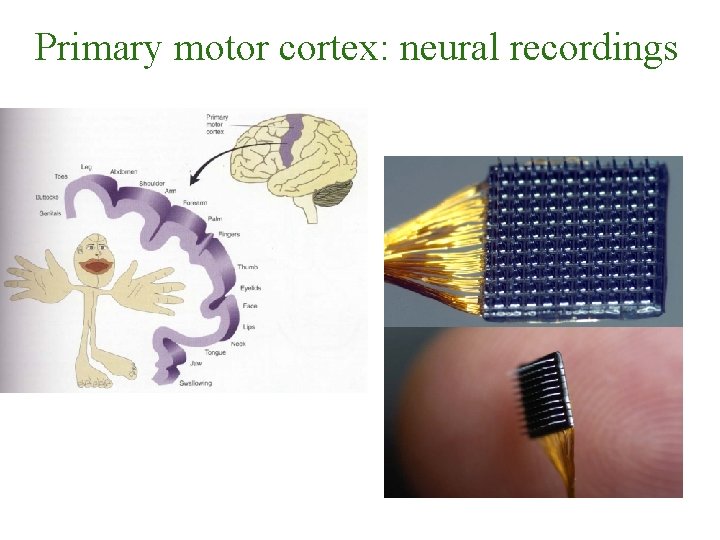
Primary motor cortex: neural recordings

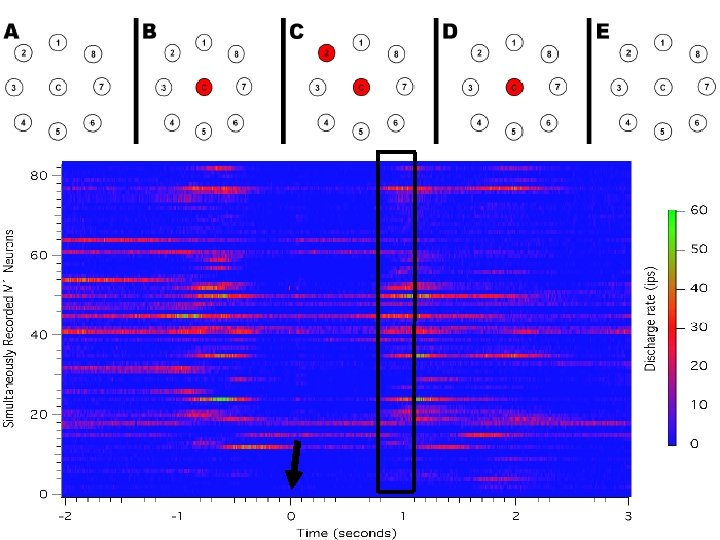
Primary motor cortex: motion direction Center-out task

Primary motor cortex: simultaneous recordings

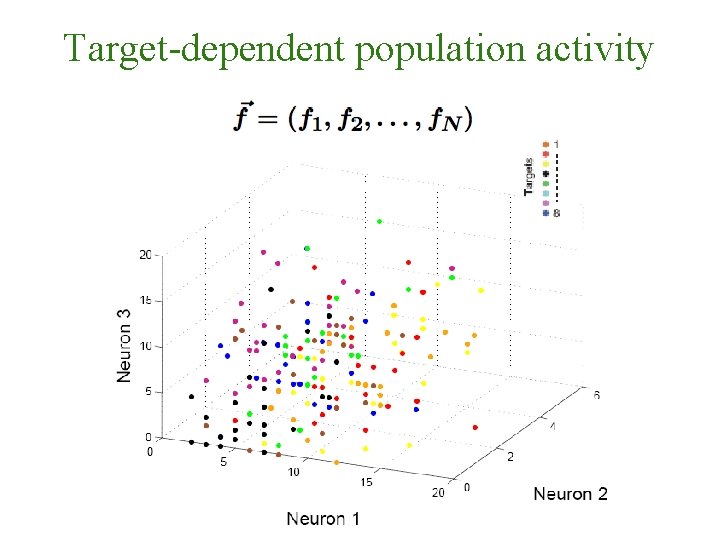
Target-dependent population activity

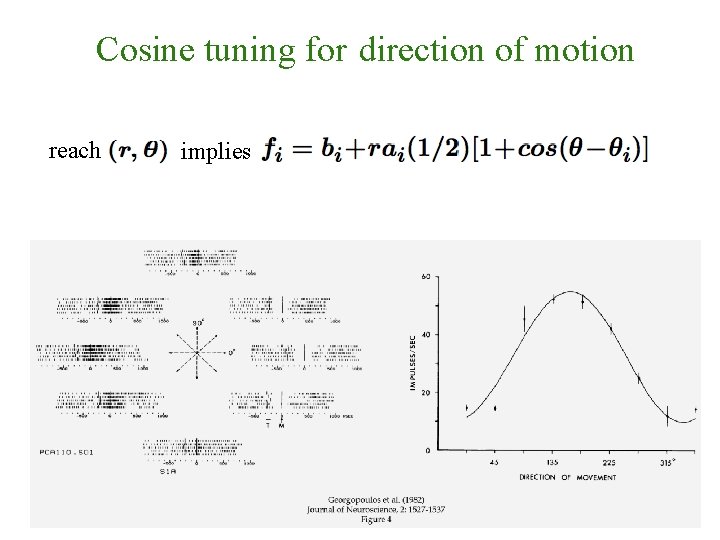
Cosine tuning for direction of motion reach implies

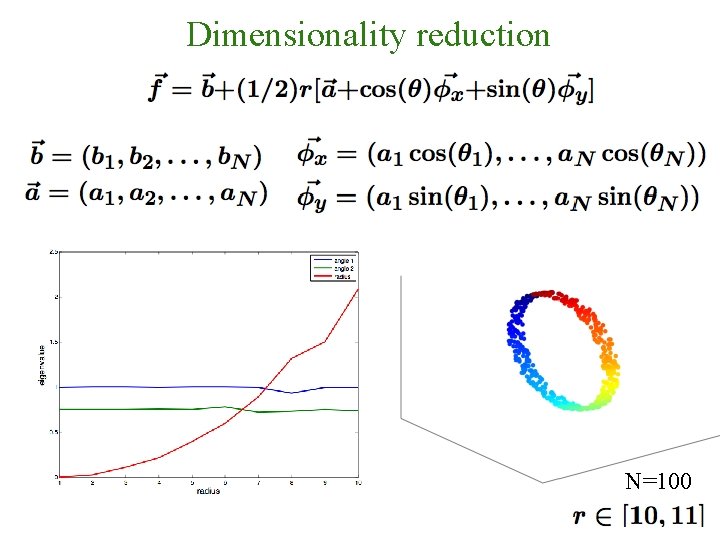
Dimensionality reduction N=100

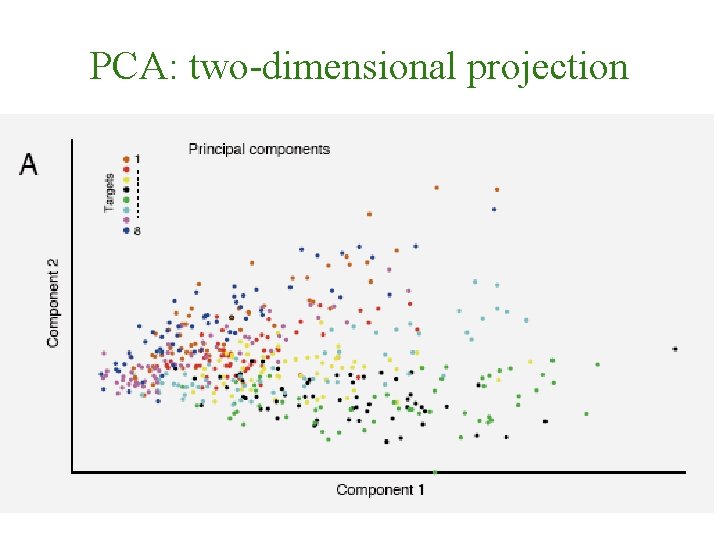
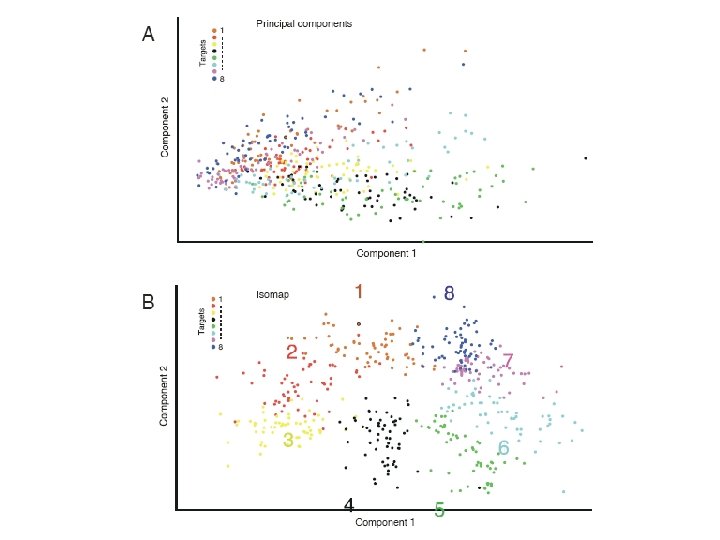
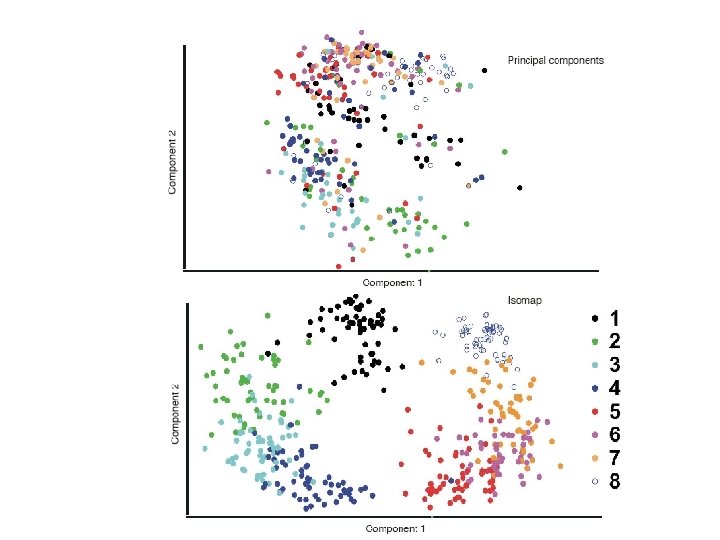
PCA: two-dimensional projection

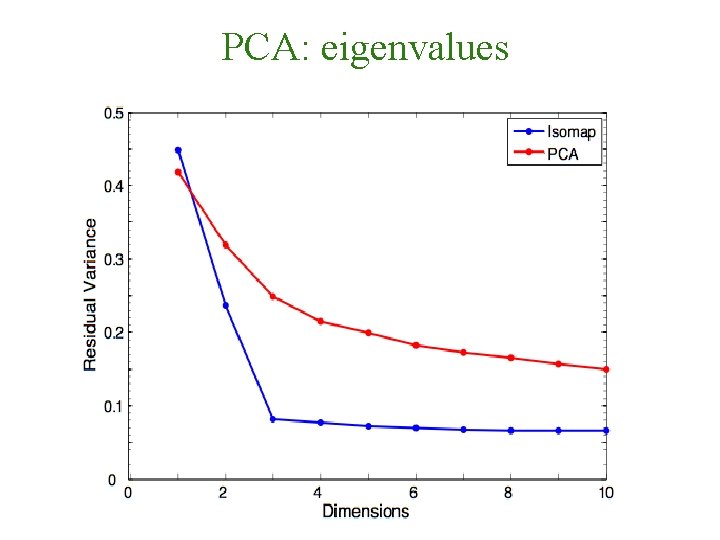
PCA: eigenvalues

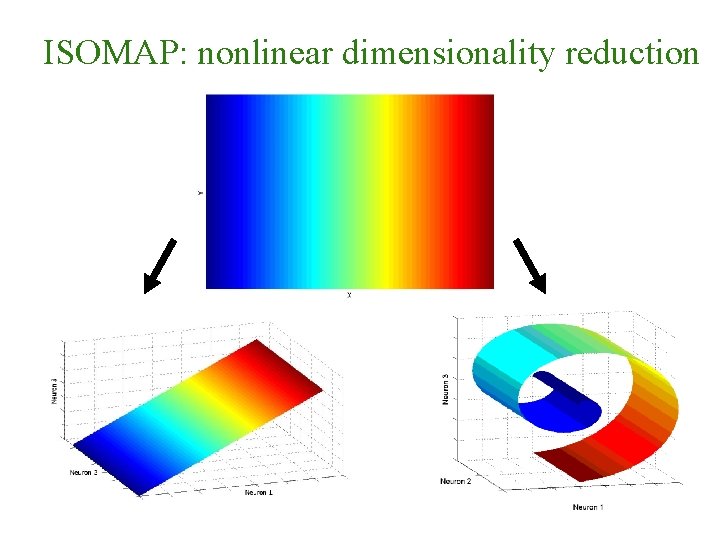
ISOMAP: nonlinear dimensionality reduction

Multidimensional scaling A method for embedding objects in a low dimensional space such that Euclidean distances between the corresponding points reproduce as well as possible an empirical matrix of dissimilarities. A B C D A 0 7 2 3 B C 7 2 0 4. 5 0 6 5 D 3 6 5 0

Multidimensional scaling Consider data in the form of N-dimensional vectors. For us, the data is the N-dimensional vector of firing rates associated with each reach Multiple reaches result in an Nx. M matrix: If the matrix is hidden from us, but we are given instead an Mx. M matrix of squared distances between data points, can ? we reconstruct the matrix

Multidimensional scaling If the distances are Euclidean to begin with: the scalar product between data points can be written as: In matrix form, and where is the Mx. M centering matrix:

Multidimensional scaling In matrix form: From this equation the data matrix can be easily obtained: If the distance matrix to which this calculation is applied is based on Euclidean distances, this process allows us to compute the data matrix X from the distance matrix S. A reduction of the dimensionality of the original data space follows from truncation of the number of eigenvalues from M to K, and the corresponding restriction in the number of eigenvectors used to reconstruct X. It can be proved that this truncation is equivalent to PCA, which is based on the diagonalization of.

ISOMAP: a nonlinear embedding Tenenbaum et al. 2000

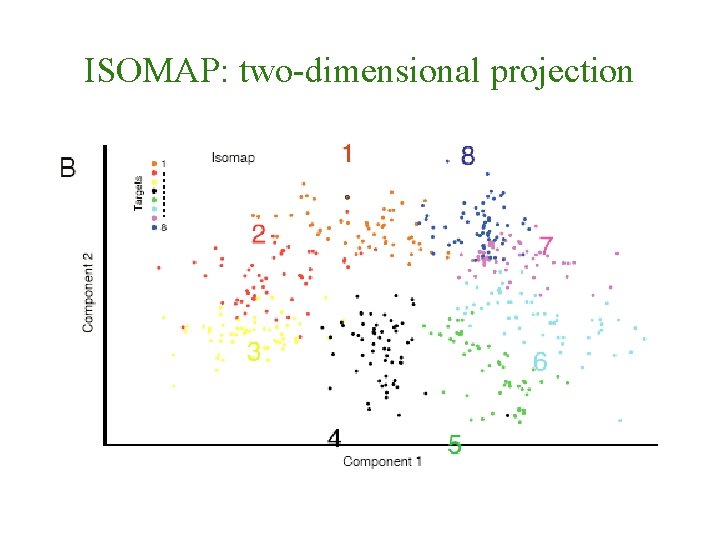
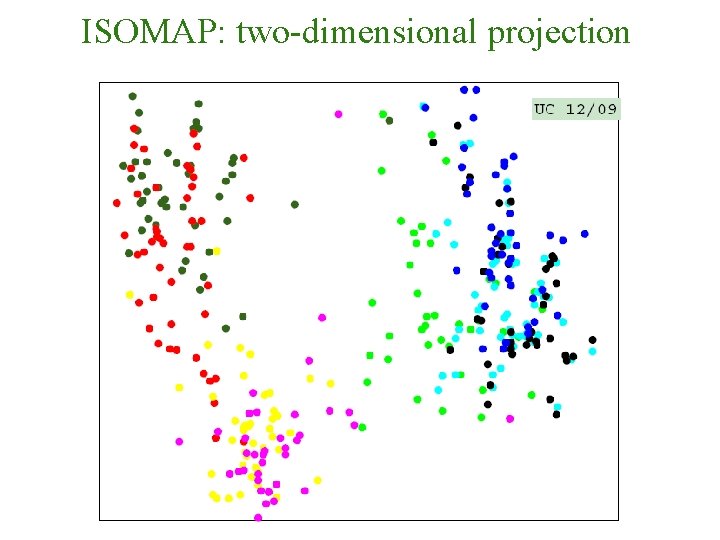
ISOMAP: two-dimensional projection

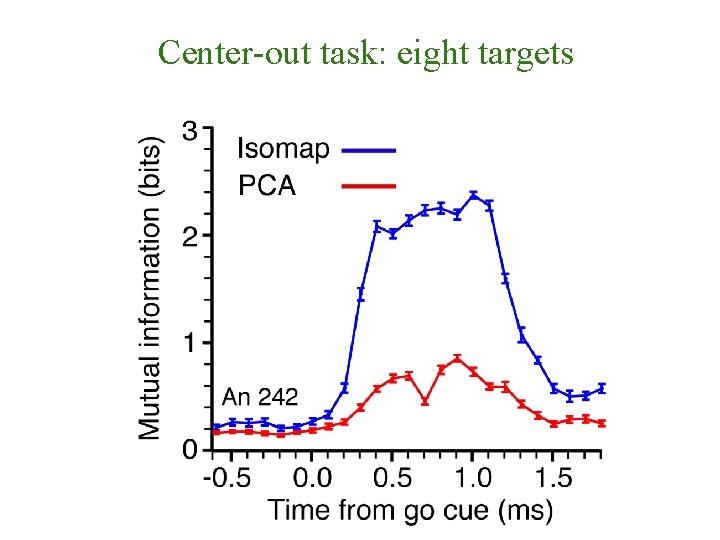
Mutual information How much can we learn about the class that a given point belongs to by knowing its location in space?

Center-out task: eight targets

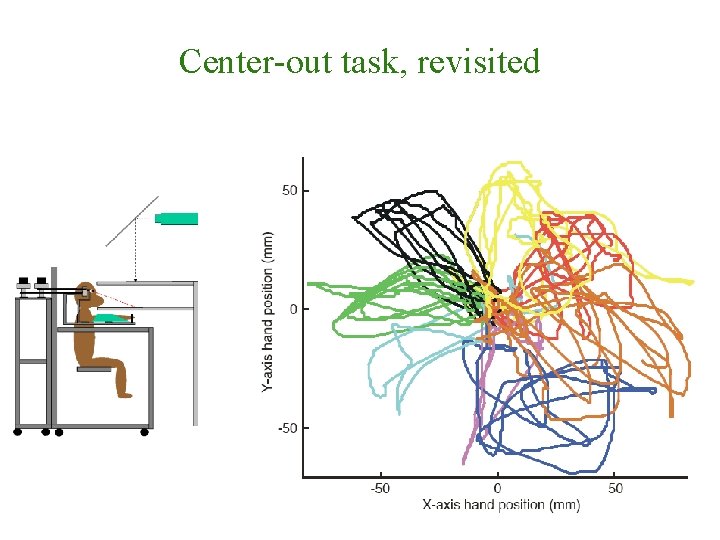
Center-out task, revisited

ISOMAP: two-dimensional projection

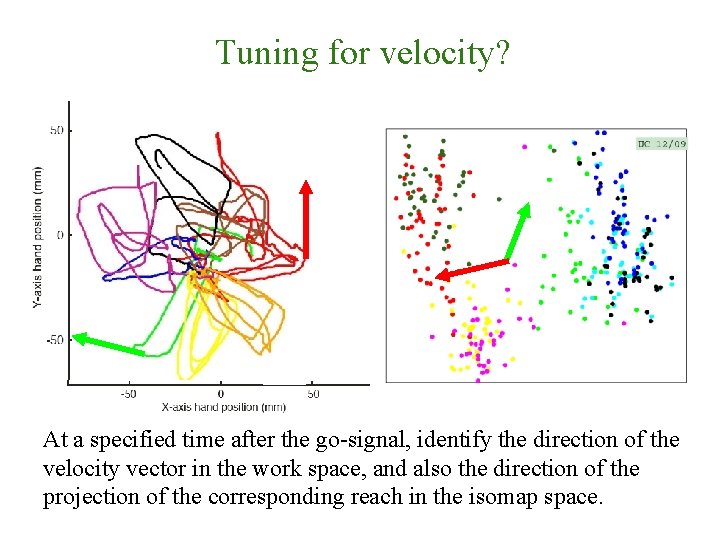
Tuning for velocity? At a specified time after the go-signal, identify the direction of the velocity vector in the work space, and also the direction of the projection of the corresponding reach in the isomap space.

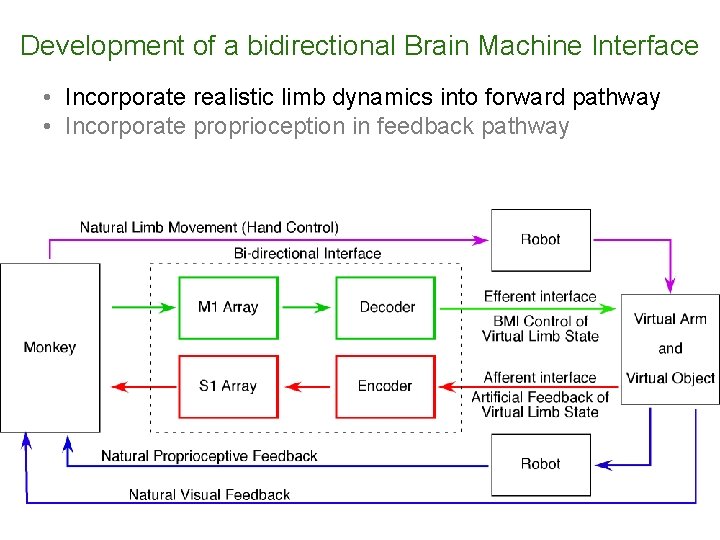
Development of a bidirectional Brain Machine Interface • Incorporate realistic limb dynamics into forward pathway • Incorporate proprioception in feedback pathway

Motion predictions from M 1 activity * simultaneous recordings of population activity can be analyzed with techniques fundamentally different techniques than those used for single neurons * for limb reaches, the population activity defines a nonlinear low dimensional manifold, whose intrinsic coordinates capture task-relevant kinematic dimensions * this technique enables the visualization of high-dimensional neural data with minimal information loss