Decoders Reference Chapter 3 Moris Mano 4 th

Decoders Reference: Chapter 3 Moris Mano 4 th Edition

Minterms Total Variables = 3 All Possible Minterms/Combinations/Product Terms = 2^3 = 8

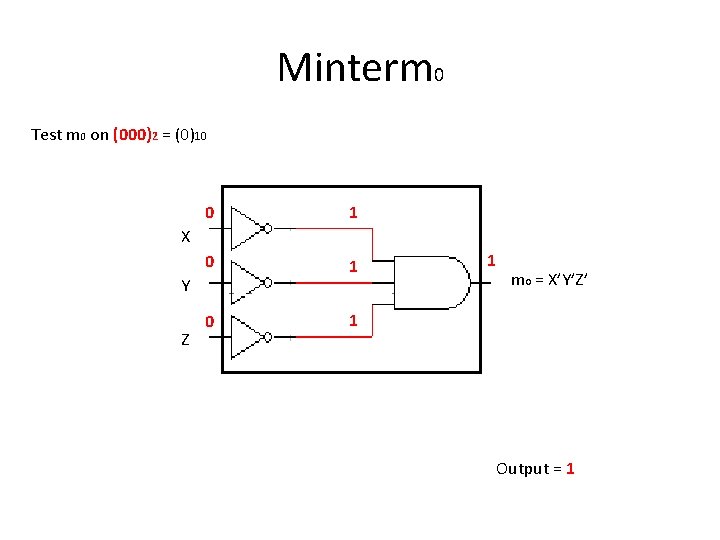
Minterm 0 Test m 0 on (000)2 = (0)10 0 1 0 1 X Y Z 1 m 0 = X’Y’Z’ Output = 1

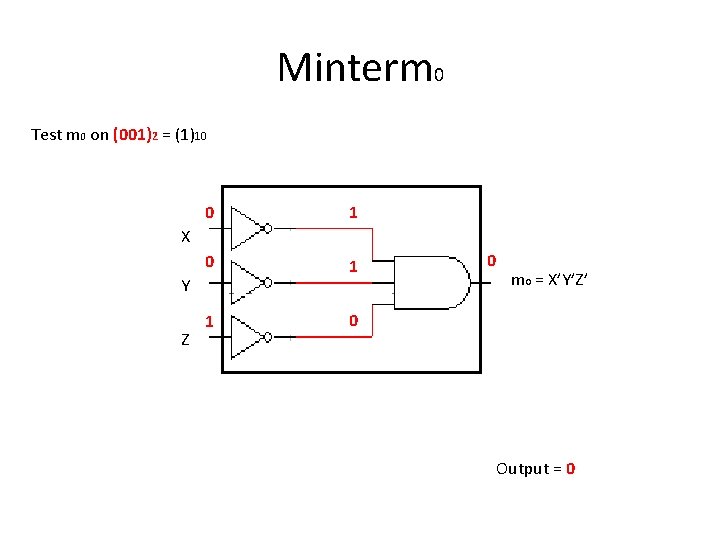
Minterm 0 Test m 0 on (001)2 = (1)10 0 1 1 0 X Y Z 0 m 0 = X’Y’Z’ Output = 0

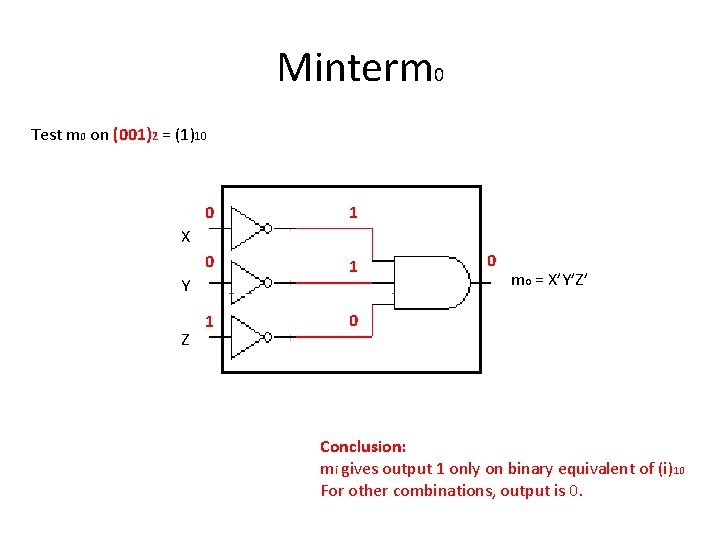
Minterm 0 Test m 0 on (001)2 = (1)10 0 1 1 0 X Y Z 0 m 0 = X’Y’Z’ Conclusion: mi gives output 1 only on binary equivalent of (i)10 For other combinations, output is 0.

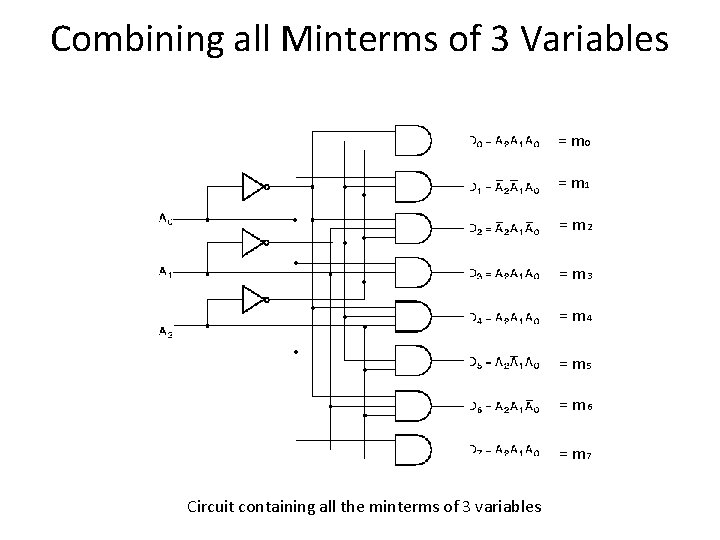
Combining all Minterms of 3 Variables = m 0 = m 1 = m 2 = m 3 = m 4 = m 5 = m 6 = m 7 Circuit containing all the minterms of 3 variables

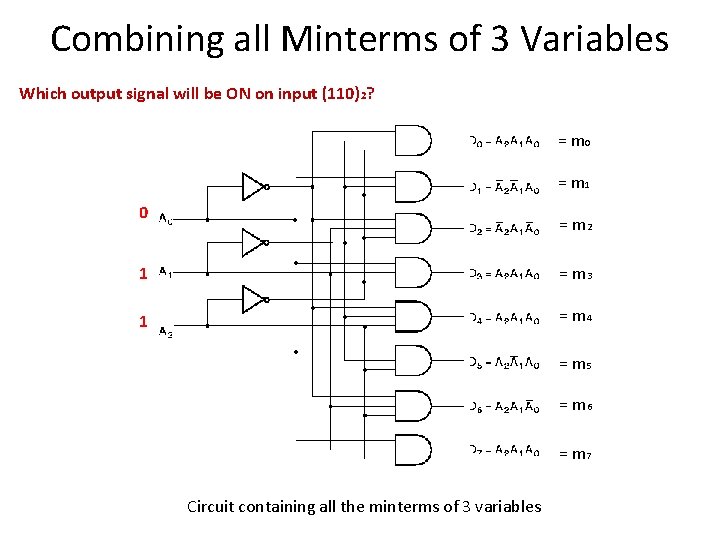
Combining all Minterms of 3 Variables Which output signal will be ON on input (110)2? = m 0 = m 1 0 = m 2 1 = m 3 1 = m 4 = m 5 = m 6 = m 7 Circuit containing all the minterms of 3 variables

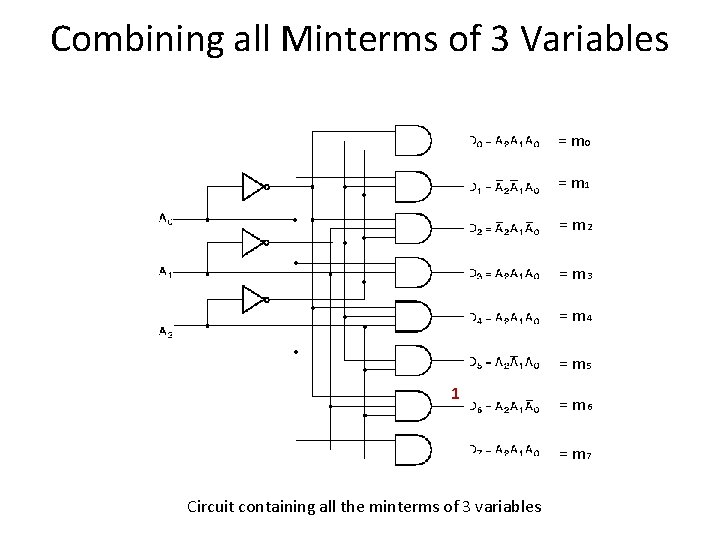
Combining all Minterms of 3 Variables = m 0 = m 1 = m 2 = m 3 = m 4 = m 5 1 = m 6 = m 7 Circuit containing all the minterms of 3 variables

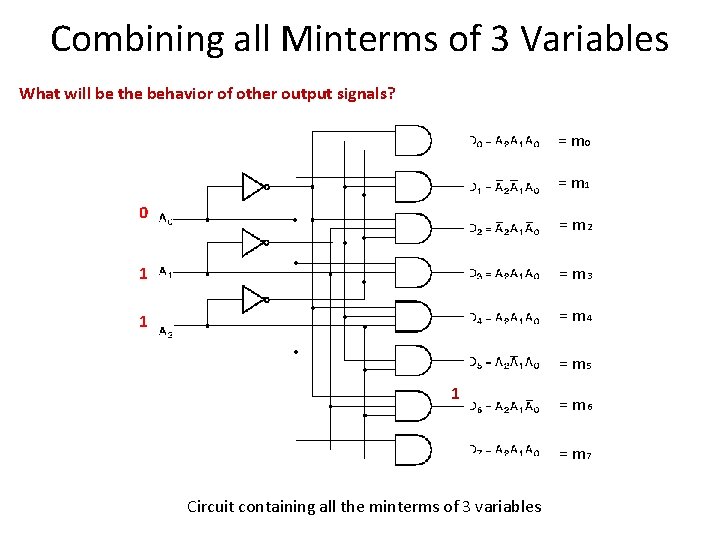
Combining all Minterms of 3 Variables What will be the behavior of other output signals? = m 0 = m 1 0 = m 2 1 = m 3 1 = m 4 = m 5 1 = m 6 = m 7 Circuit containing all the minterms of 3 variables

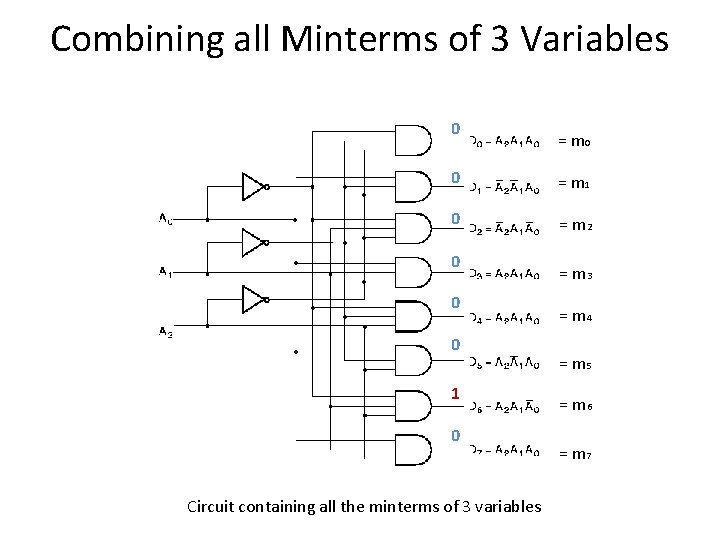
Combining all Minterms of 3 Variables 0 = m 0 0 = m 1 0 = m 2 0 0 0 1 0 Circuit containing all the minterms of 3 variables = m 3 = m 4 = m 5 = m 6 = m 7

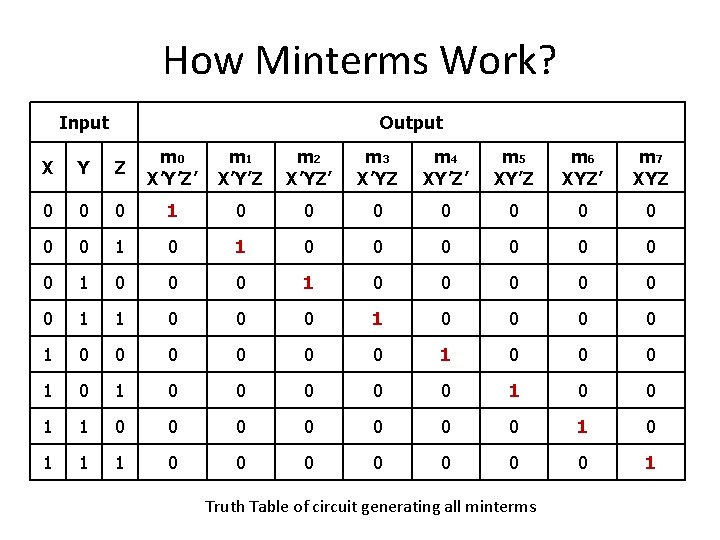
How Minterms Work? Input Output X Y Z m 0 X’Y’Z’ m 1 X’Y’Z m 2 X’YZ’ m 3 X’YZ m 4 XY’Z’ m 5 XY’Z m 6 XYZ’ m 7 XYZ 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 Truth Table of circuit generating all minterms

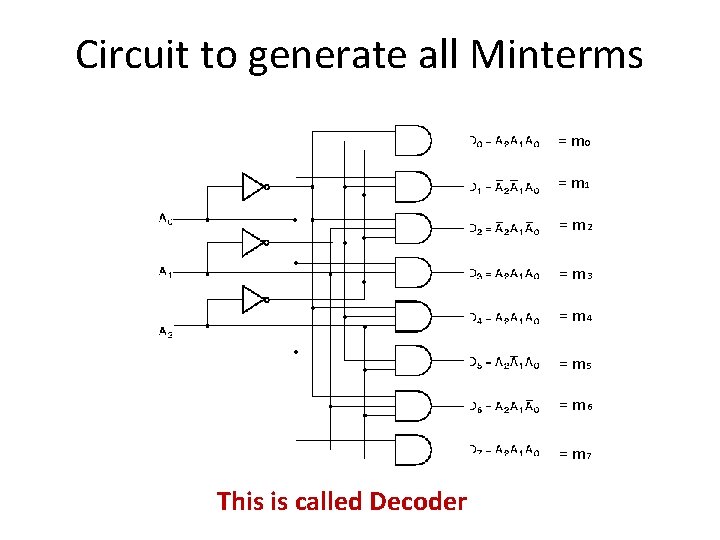
Circuit to generate all Minterms = m 0 = m 1 = m 2 = m 3 = m 4 = m 5 = m 6 = m 7 This is called Decoder

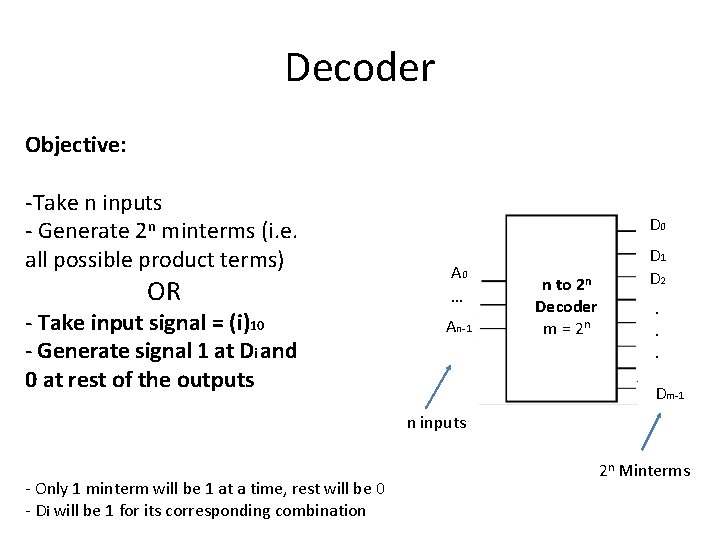
Decoder Objective: -Take n inputs - Generate 2 n minterms (i. e. all possible product terms) OR - Take input signal = (i)10 - Generate signal 1 at Di and 0 at rest of the outputs D 0 A 0 … An-1 n to 2 n Decoder m = 2 n D 1 D 2. . . Dm-1 n inputs - Only 1 minterm will be 1 at a time, rest will be 0 - Di will be 1 for its corresponding combination 2 n Minterms

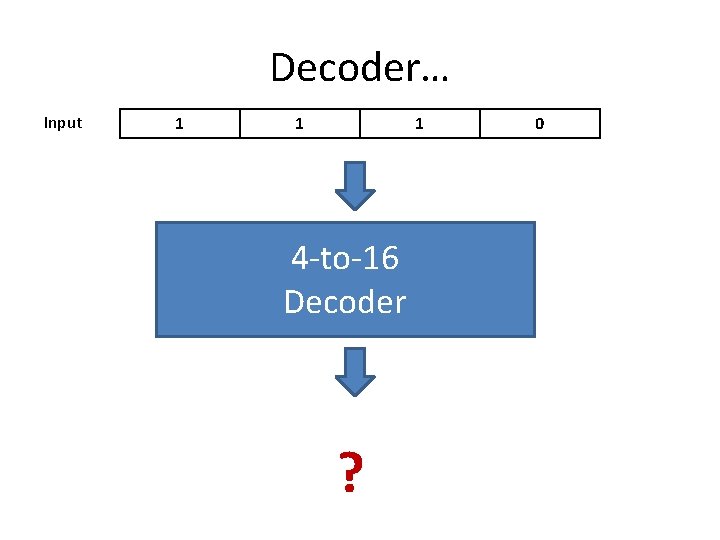
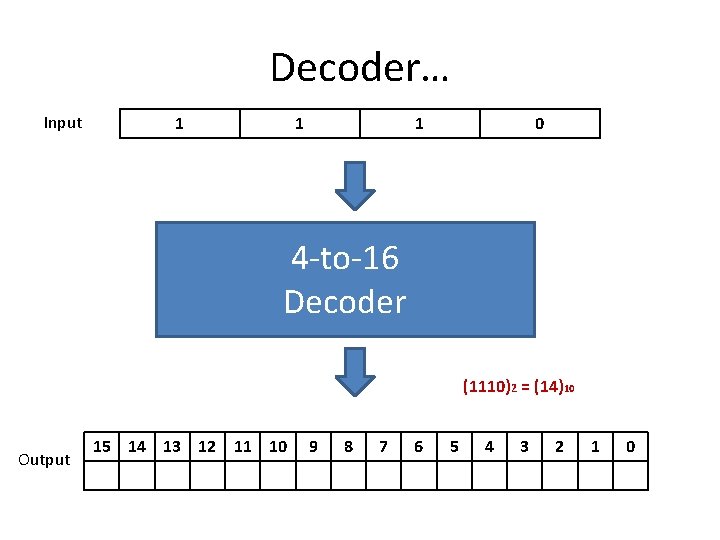
Decoder… Input 1 1 1 4 -to-16 Decoder ? 0

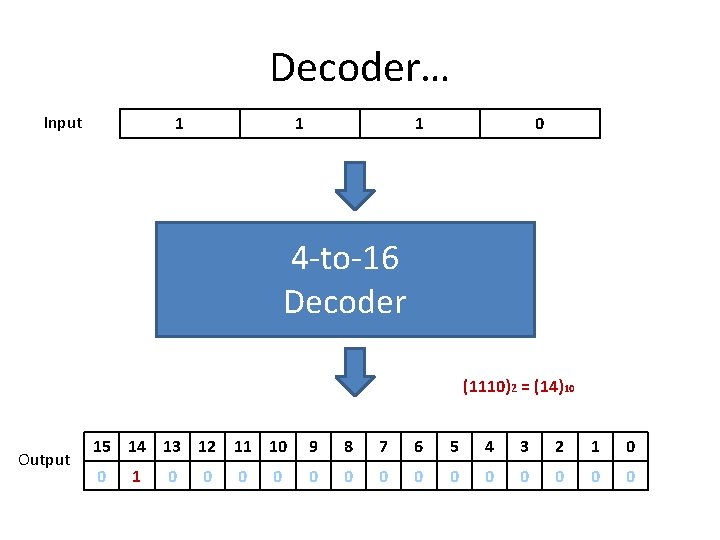
Decoder… Input 1 1 1 0 4 -to-16 Decoder (1110)2 = (14)10 Output 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Decoder… Input 1 1 1 0 4 -to-16 Decoder (1110)2 = (14)10 Output 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 0 0 1 0 0

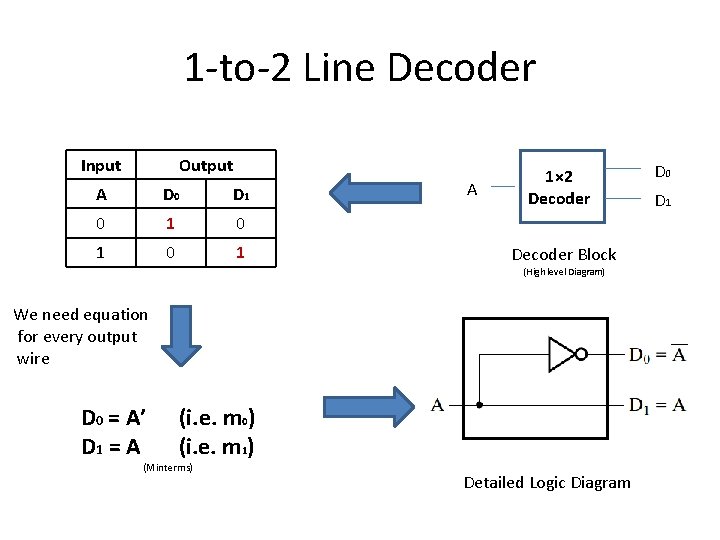
1 -to-2 Line Decoder Input Output A D 0 D 1 0 1 0 1 A 1× 2 Decoder Block (High level Diagram) We need equation for every output wire D 0 = A’ D 1 = A (i. e. m 0) (i. e. m 1) (Minterms) Detailed Logic Diagram D 0 D 1

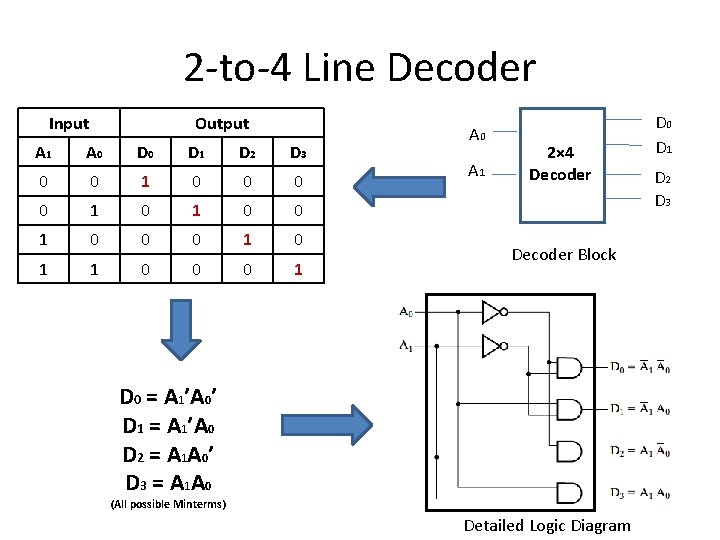
2 -to-4 Line Decoder Input Output A 1 A 0 D 1 D 2 D 3 0 0 1 0 0 1 0 0 0 1 A 0 A 1 2× 4 Decoder Block D 0 = A 1’A 0’ D 1 = A 1’A 0 D 2 = A 1 A 0 ’ D 3 = A 1 A 0 (All possible Minterms) Detailed Logic Diagram D 0 D 1 D 2 D 3

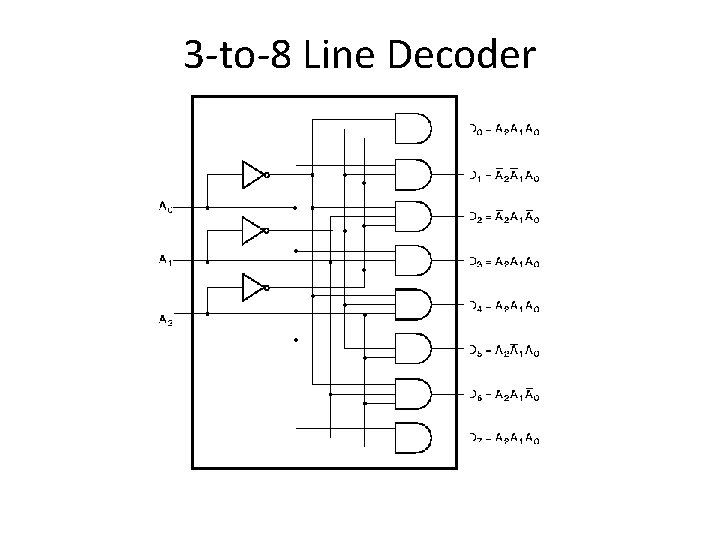
3 -to-8 Line Decoder

Decoder with Enable Input

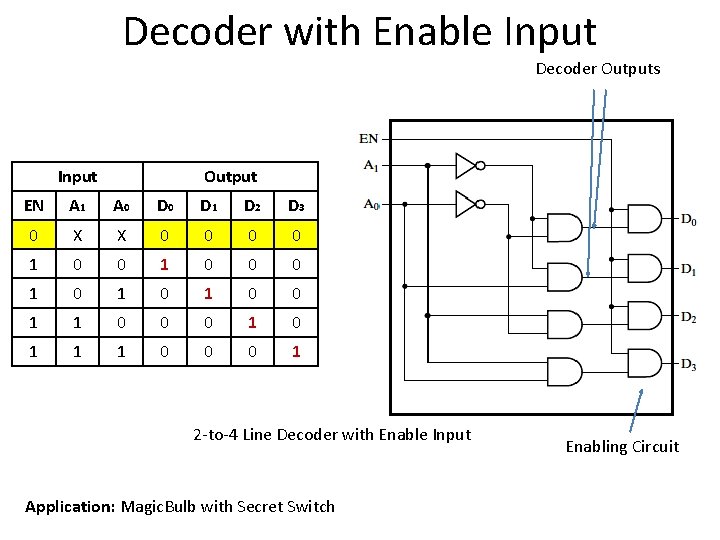
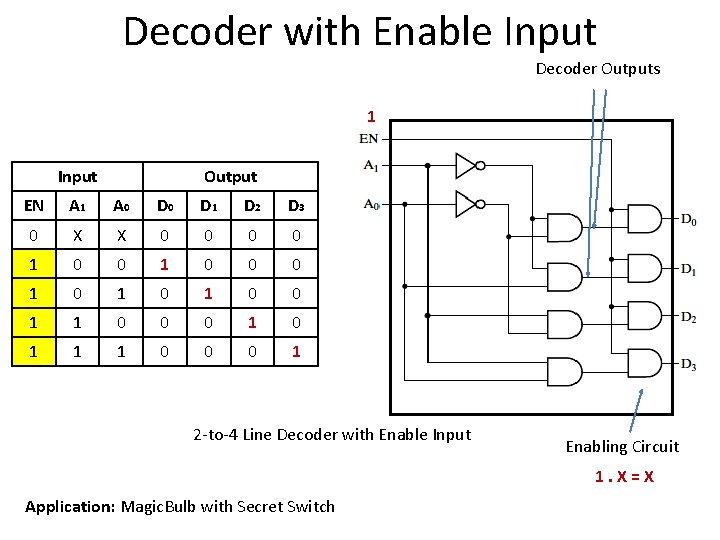
Decoder with Enable Input Decoder Outputs Input Output EN A 1 A 0 D 1 D 2 D 3 0 X X 0 0 1 0 1 0 0 1 1 0 0 0 1 2 -to-4 Line Decoder with Enable Input Application: Magic. Bulb with Secret Switch Enabling Circuit

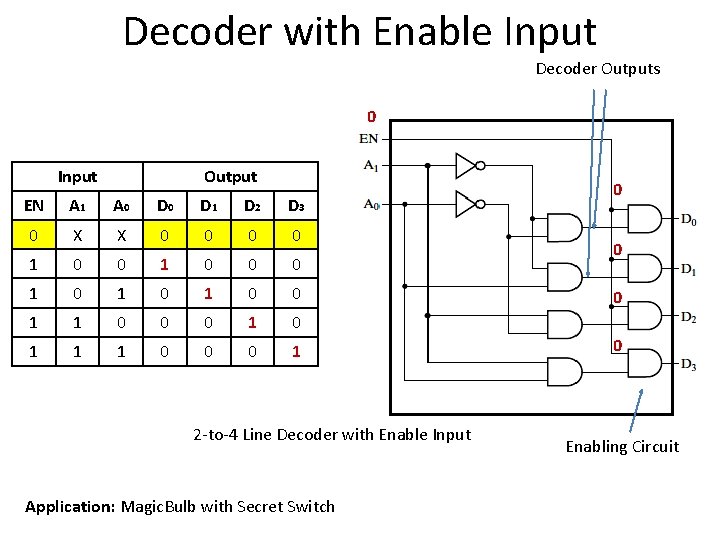
Decoder with Enable Input Decoder Outputs 0 Input Output EN A 1 A 0 D 1 D 2 D 3 0 X X 0 0 1 0 1 0 0 1 1 0 0 0 1 2 -to-4 Line Decoder with Enable Input Application: Magic. Bulb with Secret Switch 0 0 Enabling Circuit

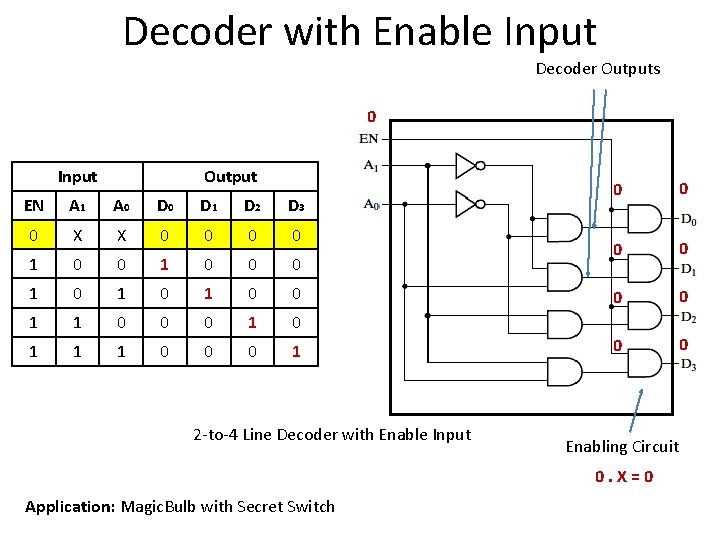
Decoder with Enable Input Decoder Outputs 0 Input Output EN A 1 A 0 D 1 D 2 D 3 0 X X 0 0 1 0 1 0 0 1 1 0 0 0 1 2 -to-4 Line Decoder with Enable Input 0 0 0 0 Enabling Circuit 0. X=0 Application: Magic. Bulb with Secret Switch

Decoder with Enable Input Decoder Outputs 1 Input Output EN A 1 A 0 D 1 D 2 D 3 0 X X 0 0 1 0 1 0 0 1 1 0 0 0 1 2 -to-4 Line Decoder with Enable Input Enabling Circuit 1. X=X Application: Magic. Bulb with Secret Switch

Implementing Functions using Decoder

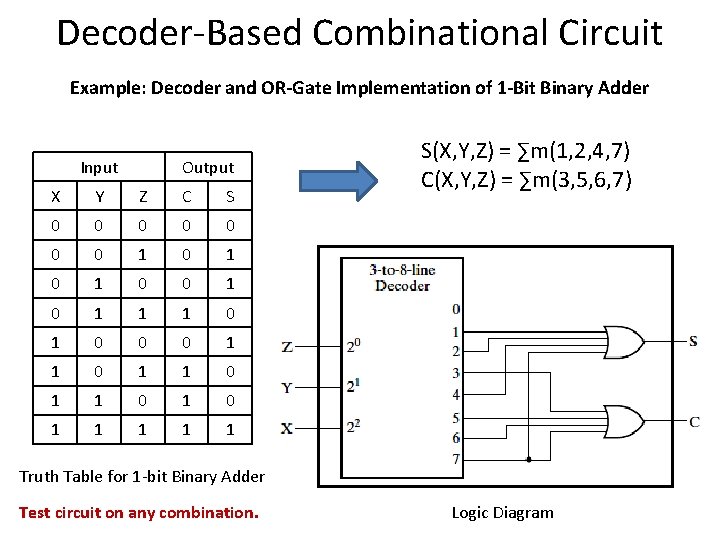
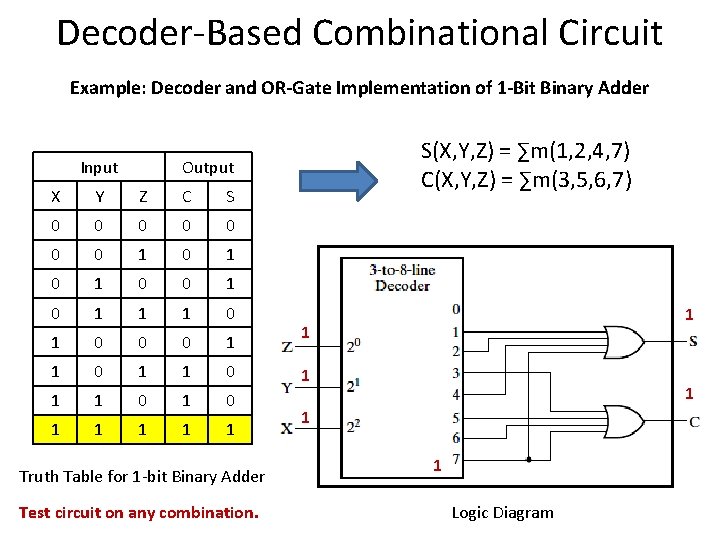
Decoder-Based Combinational Circuit Example: Decoder and OR-Gate Implementation of 1 -Bit Binary Adder Input Output X Y Z C S 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1 Truth Table for 1 -bit Binary Adder S(X, Y, Z) = ∑m(1, 2, 4, 7) C(X, Y, Z) = ∑m(3, 5, 6, 7)

Decoder-Based Combinational Circuit Example: Decoder and OR-Gate Implementation of 1 -Bit Binary Adder Input Output X Y Z C S 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1 S(X, Y, Z) = ∑m(1, 2, 4, 7) C(X, Y, Z) = ∑m(3, 5, 6, 7) Truth Table for 1 -bit Binary Adder Test circuit on any combination. Logic Diagram

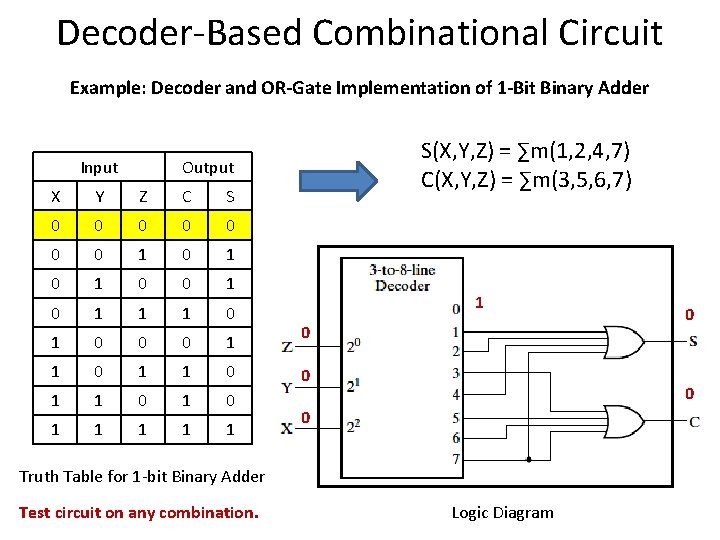
Decoder-Based Combinational Circuit Example: Decoder and OR-Gate Implementation of 1 -Bit Binary Adder Input S(X, Y, Z) = ∑m(1, 2, 4, 7) C(X, Y, Z) = ∑m(3, 5, 6, 7) Output X Y Z C S 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1 0 0 Truth Table for 1 -bit Binary Adder Test circuit on any combination. 0 Logic Diagram

Decoder-Based Combinational Circuit Example: Decoder and OR-Gate Implementation of 1 -Bit Binary Adder Input S(X, Y, Z) = ∑m(1, 2, 4, 7) C(X, Y, Z) = ∑m(3, 5, 6, 7) Output X Y Z C S 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1 0 0 1 1 Truth Table for 1 -bit Binary Adder Test circuit on any combination. Logic Diagram

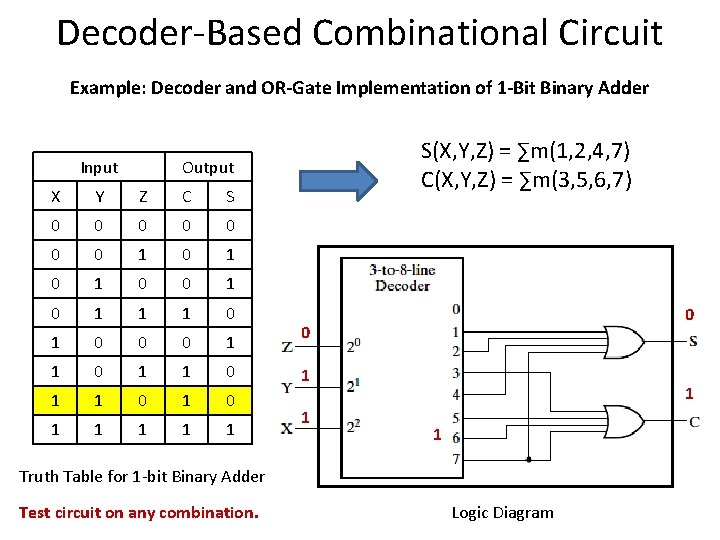
Decoder-Based Combinational Circuit Example: Decoder and OR-Gate Implementation of 1 -Bit Binary Adder Input S(X, Y, Z) = ∑m(1, 2, 4, 7) C(X, Y, Z) = ∑m(3, 5, 6, 7) Output X Y Z C S 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1 Truth Table for 1 -bit Binary Adder Test circuit on any combination. 1 1 1 Logic Diagram

Decoder-Based Combinational Circuit To implement a function with n inputs and m outputs using Decoder and OR gates we need - An n x 2^n Line Decoder - m OR Gates

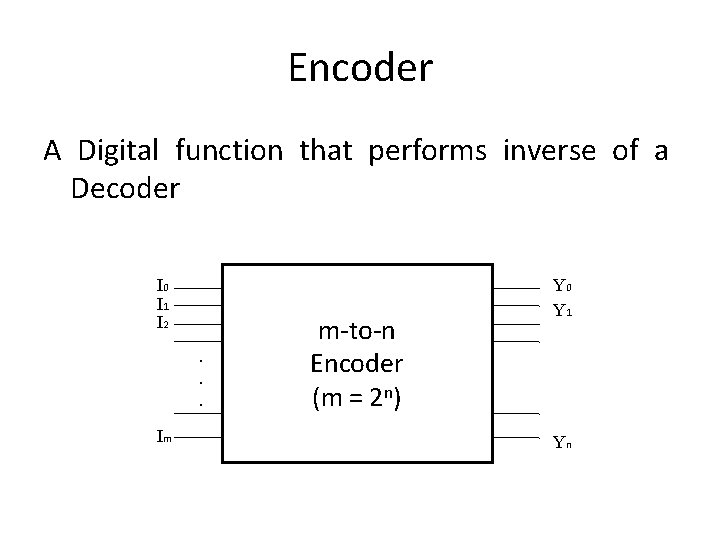
Encoder A Digital function that performs inverse of a Decoder I 0 I 1 I 2. . . Im m-to-n Encoder (m = 2 n) Y 0 Y 1 Yn

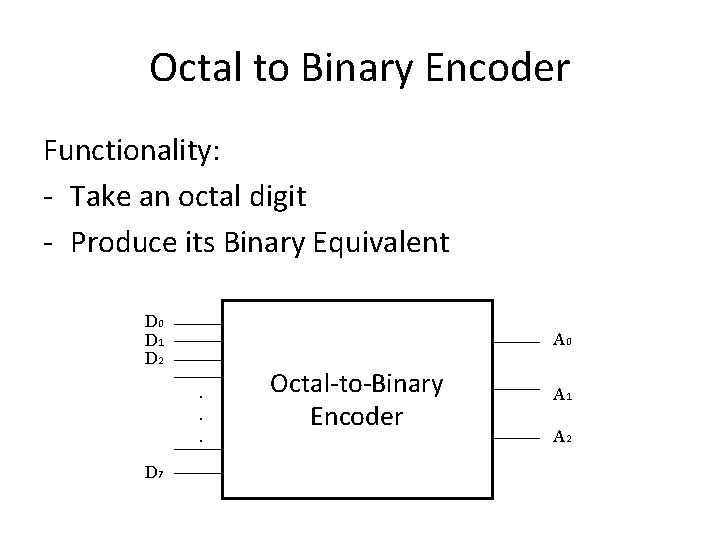
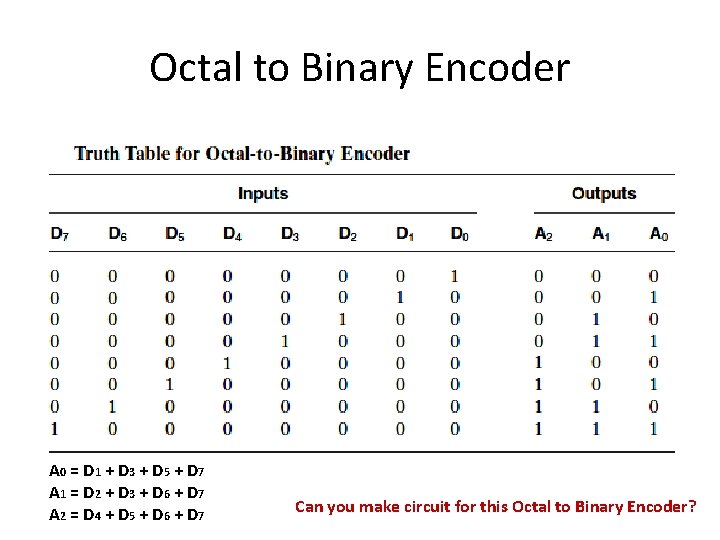
Octal to Binary Encoder Functionality: - Take an octal digit - Produce its Binary Equivalent D 0 D 1 D 2 A 0. . . D 7 Octal-to-Binary Encoder A 1 A 2

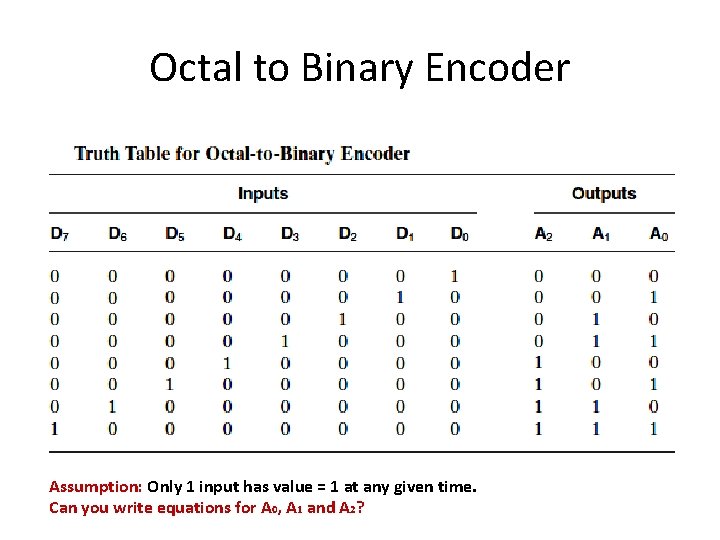
Octal to Binary Encoder Assumption: Only 1 input has value = 1 at any given time. Can you write equations for A 0, A 1 and A 2?

Octal to Binary Encoder A 0 = D 1 + D 3 + D 5 + D 7 A 1 = D 2 + D 3 + D 6 + D 7 A 2 = D 4 + D 5 + D 6 + D 7 Can you make circuit for this Octal to Binary Encoder?

Limitations of Encoder • Only 1 input should be one at a time otherwise answer will be wrong • E. g. if D 3 = D 6 = 1 A 0 = D 1 + D 3 + D 5 + D 7 = 0+1+0+0 = 1 A 1 = D 2 + D 3 + D 6 + D 7 = 0+1+1+0 = 1 A 2 = D 4 + D 5 + D 6 + D 7 = 0+0+1+0 = 1 i. e. Encoder Output = (A 2 A 1 A 0) = (111)2 = (7)8 Which is neither 3 nor 6 Solution: If D 3 and D 6 both are 1 at the same time, give priority to D 6 and output (110)2 Priority Encoder

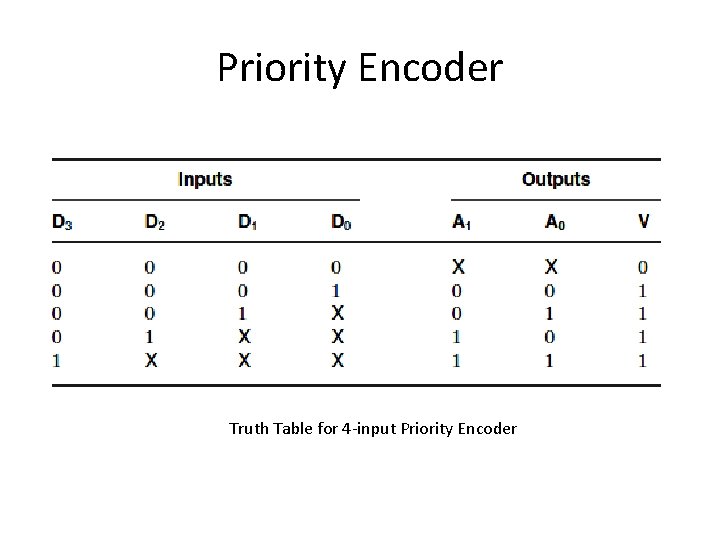
Priority Encoder Truth Table for 4 -input Priority Encoder

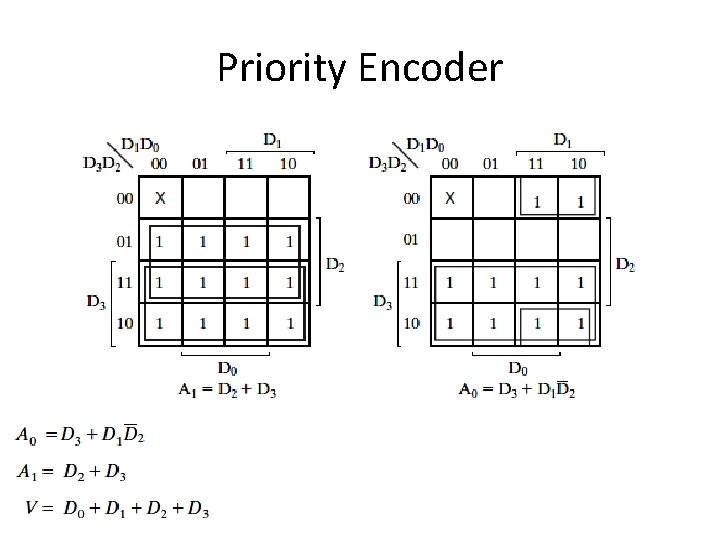
Priority Encoder

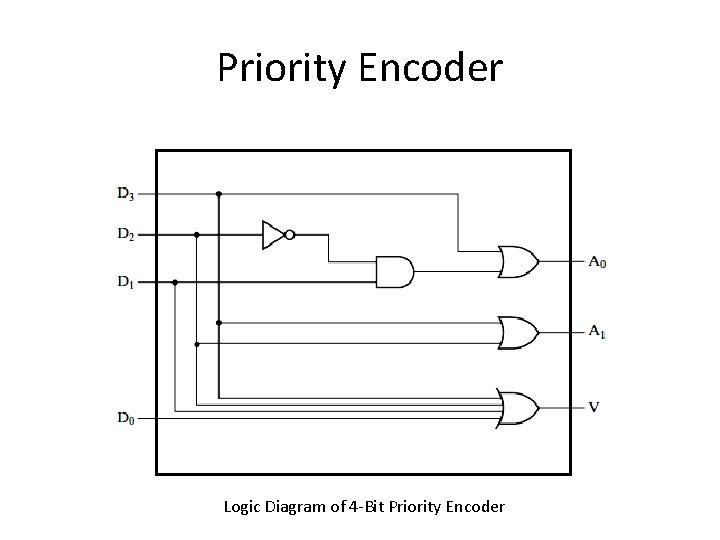
Priority Encoder Logic Diagram of 4 -Bit Priority Encoder

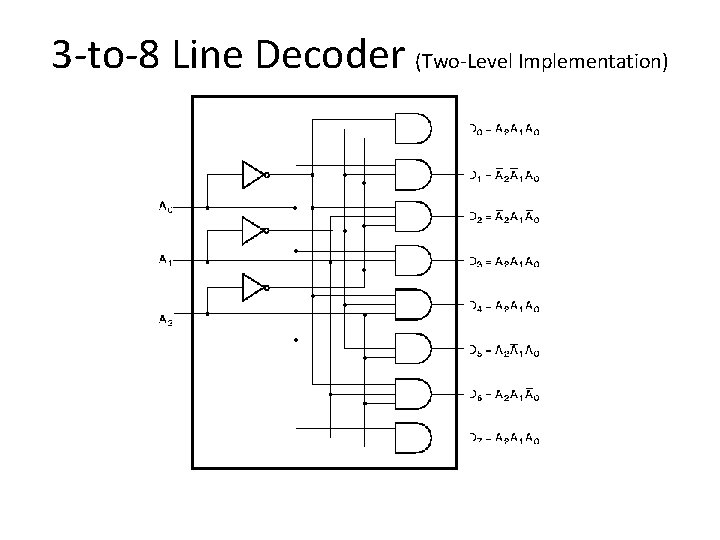
3 -to-8 Line Decoder (Two-Level Implementation)

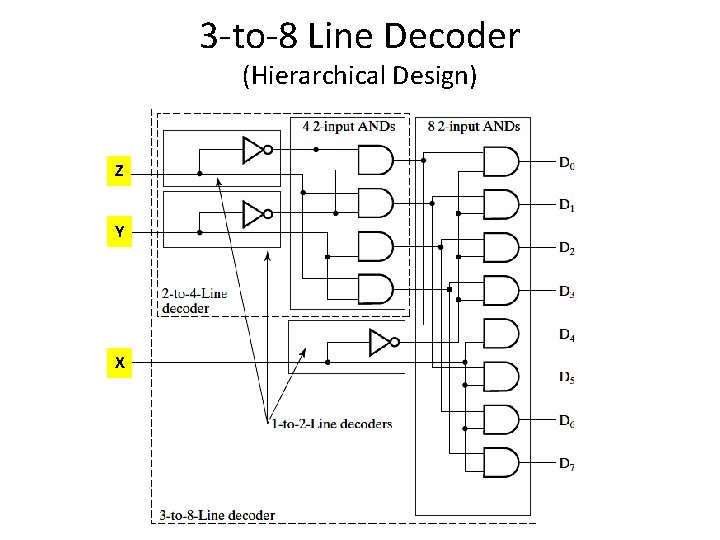
3 -to-8 Line Decoder (Hierarchical Design) Z Y X

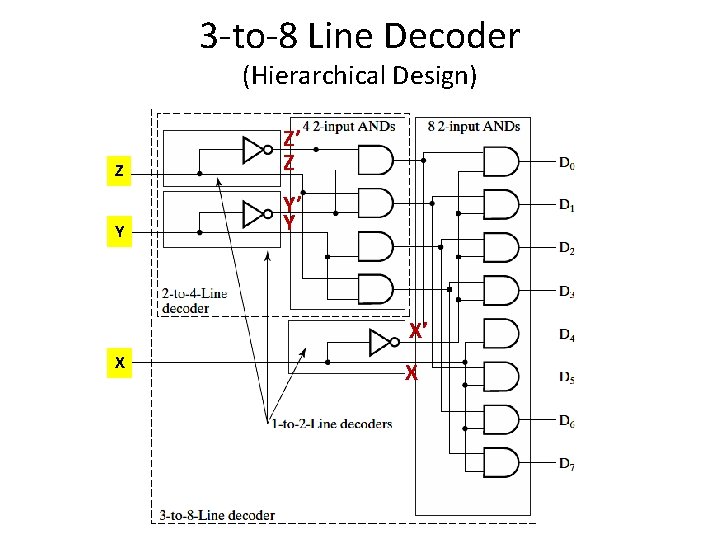
3 -to-8 Line Decoder (Hierarchical Design) Z Z’ Z Y Y’ Y X’ X X

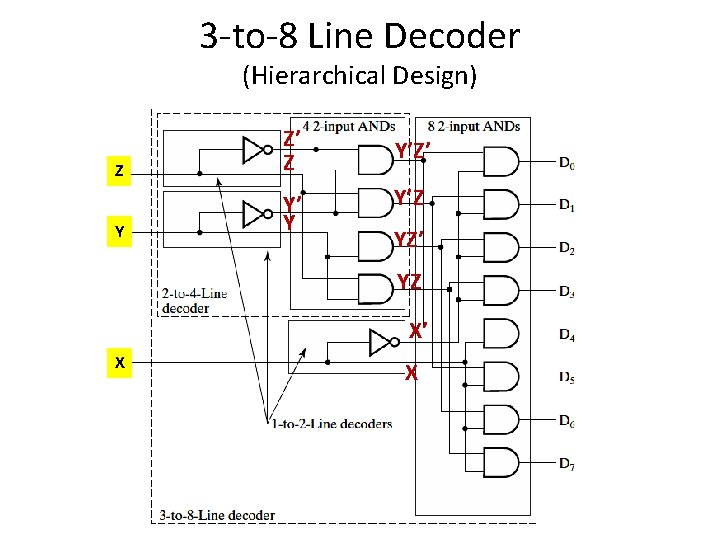
3 -to-8 Line Decoder (Hierarchical Design) Z Z’ Z Y Y’Z’ Y’Z YZ’ YZ X’ X X

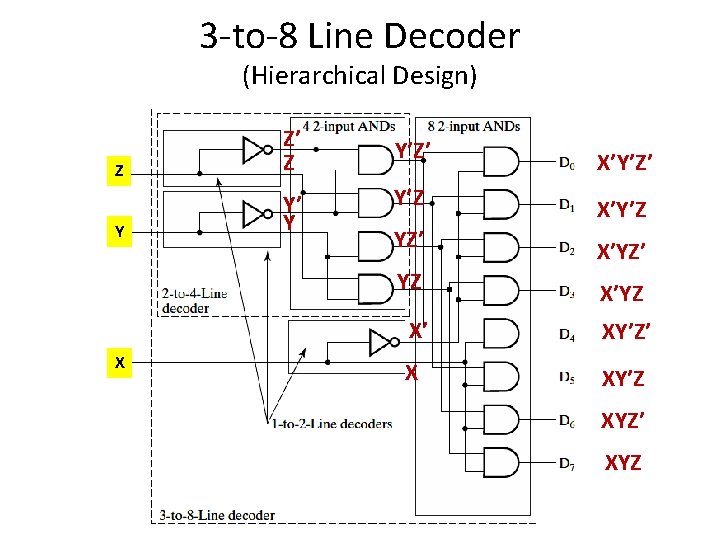
3 -to-8 Line Decoder (Hierarchical Design) Z Z’ Z Y Y’ Y X Y’Z’ X’Y’Z’ Y’Z X’Y’Z YZ’ X’YZ’ YZ X’ XY’Z’ X XY’Z XYZ’ XYZ

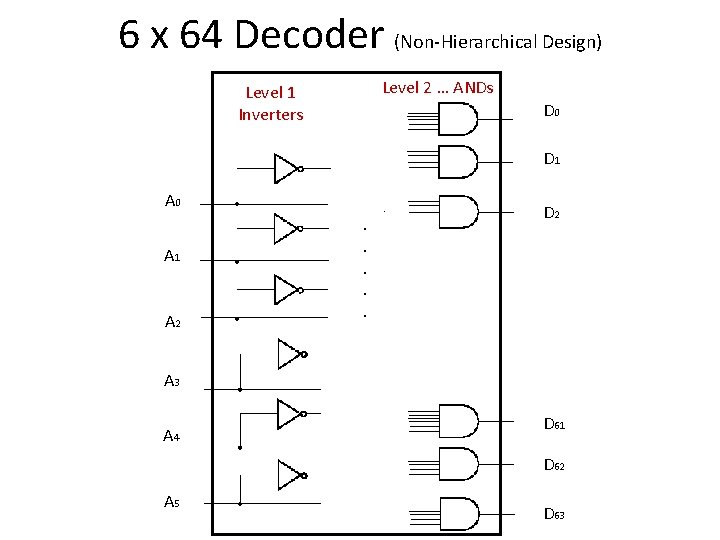
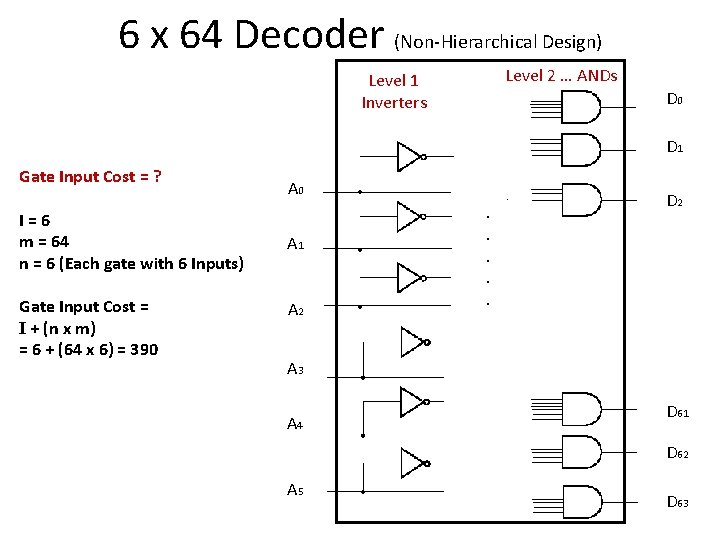
6 x 64 Decoder (Non-Hierarchical Design) Level 2 … ANDs Level 1 Inverters D 0 D 1 A 0 A 1 A 2 . . D 2 A 3 A 4 D 61 D 62 A 5 D 63

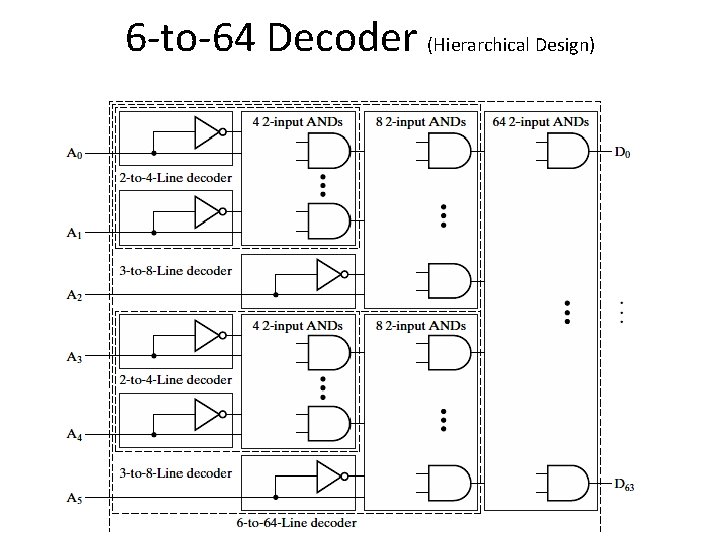
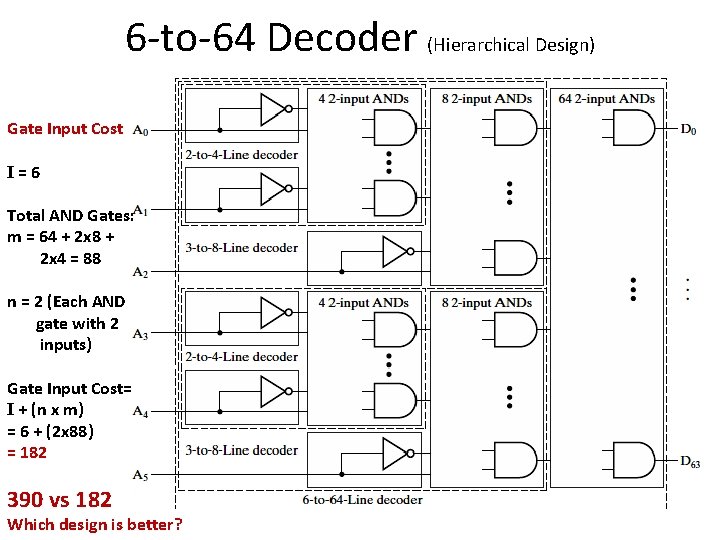
6 -to-64 Decoder (Hierarchical Design)

Two-Level Implementation vs Hierarchical Design

Gate Input Cost = I + ∑ m × n I = Total No. of inverters m = Total gates each with n input

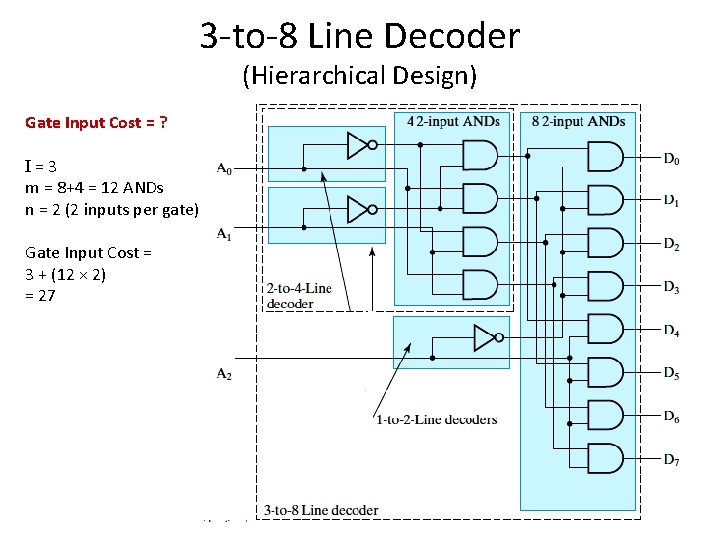
3 -to-8 Line Decoder (Hierarchical Design) Gate Input Cost = ? I=3 m = 8+4 = 12 ANDs n = 2 (2 inputs per gate) Gate Input Cost = 3 + (12 × 2) = 27

6 x 64 Decoder (Non-Hierarchical Design) Level 2 … ANDs Level 1 Inverters D 0 D 1 Gate Input Cost = ? I=6 m = 64 n = 6 (Each gate with 6 Inputs) Gate Input Cost = I + (n x m) = 6 + (64 x 6) = 390 A 1 A 2 . . D 2 A 3 A 4 D 61 D 62 A 5 D 63

6 -to-64 Decoder (Hierarchical Design) Gate Input Cost I=6 Total AND Gates: m = 64 + 2 x 8 + 2 x 4 = 88 n = 2 (Each AND gate with 2 inputs) Gate Input Cost= I + (n x m) = 6 + (2 x 88) = 182 390 vs 182 Which design is better?

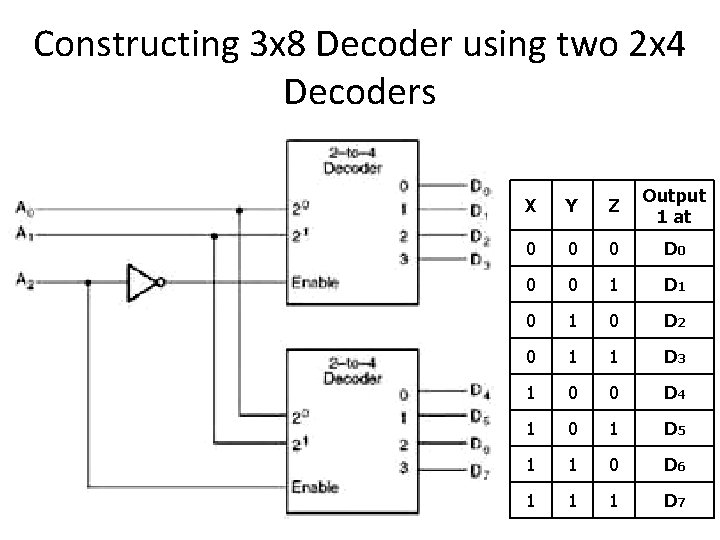
Constructing 3 x 8 Decoder using two 2 x 4 Decoders X Y Z Output 1 at 0 0 0 D 0 0 0 1 D 1 0 D 2 0 1 1 D 3 1 0 0 D 4 1 0 1 D 5 1 1 0 D 6 1 1 1 D 7

Constructing 4 x 16 Decoder using 2 x 4 Decoders Only A 0 A 1 A 2 A 3 4 x 16 Decoder D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10 D 11 D 12 D 13 D 14 D 15

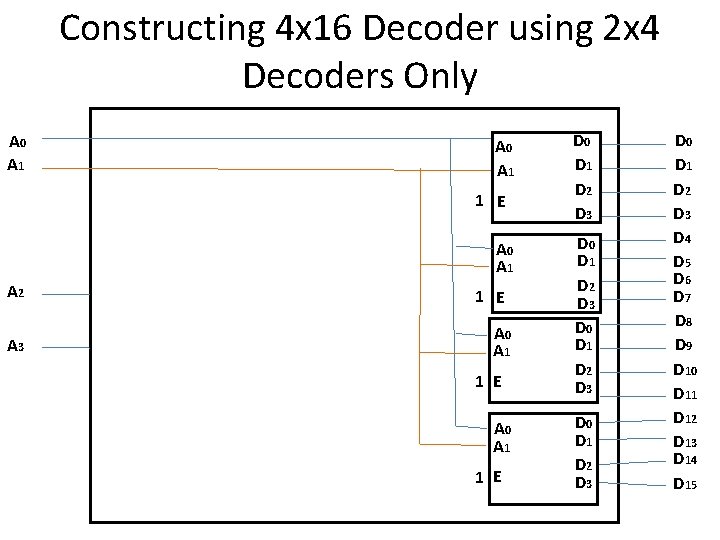
Constructing 4 x 16 Decoder using 2 x 4 Decoders Only A 0 A 1 1 E A 0 A 1 A 2 A 3 1 E A 0 A 1 1 E D 0 D 1 D 2 D 3 D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10 D 11 D 12 D 13 D 14 D 15

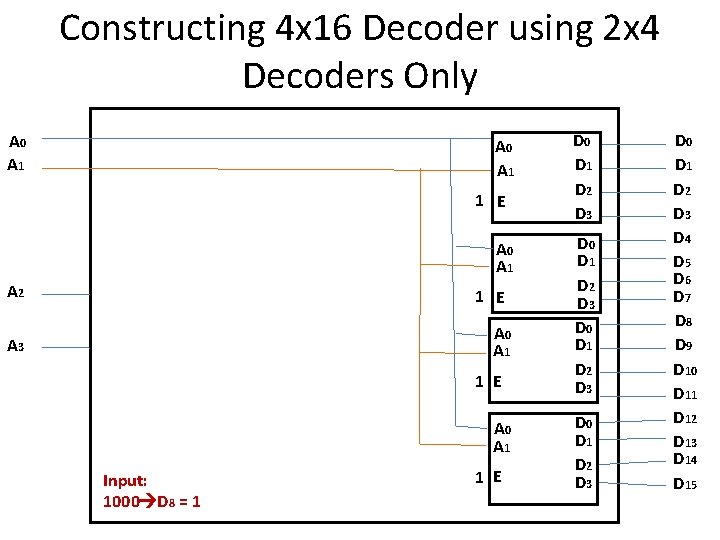
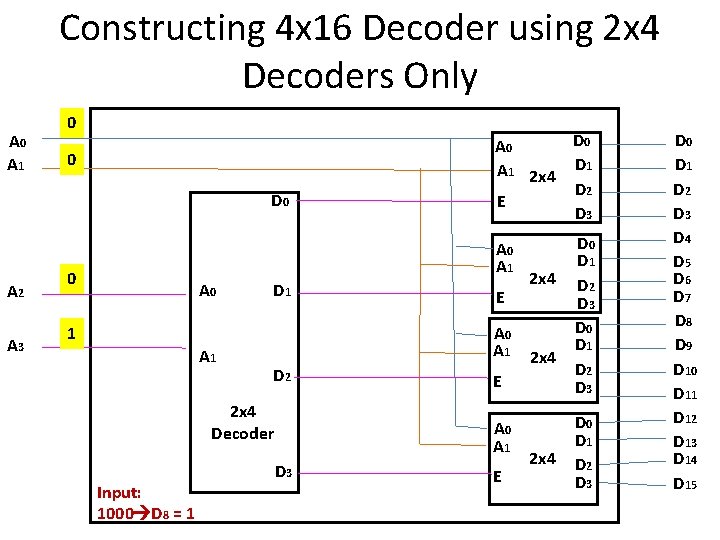
Constructing 4 x 16 Decoder using 2 x 4 Decoders Only A 0 A 1 1 E A 0 A 1 A 2 1 E A 0 A 1 A 3 1 E A 0 A 1 Input: 1000 D 8 = 1 1 E D 0 D 1 D 2 D 3 D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10 D 11 D 12 D 13 D 14 D 15

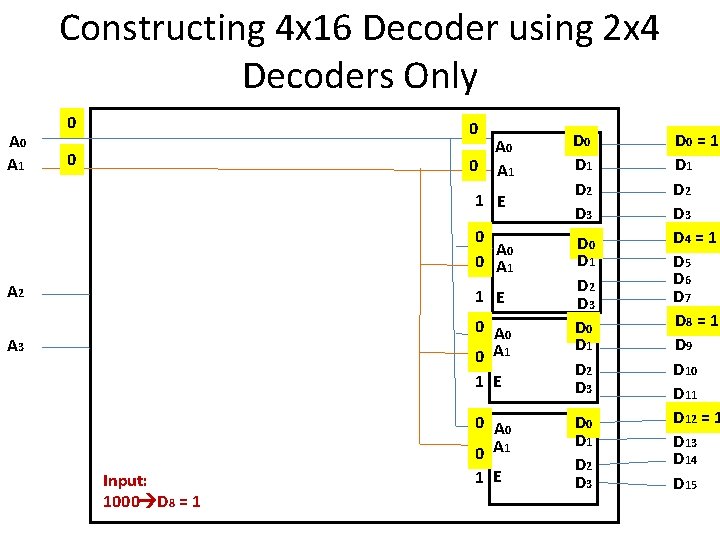
Constructing 4 x 16 Decoder using 2 x 4 Decoders Only A 0 A 1 0 1 E 0 A 0 0 A 1 D 0 D 1 D 2 D 3 A 2 1 E A 3 0 A 0 0 A 1 1 E D 0 D 1 D 2 D 3 Input: 1000 D 8 = 1 D 0 = 1 D 2 D 3 D 4 = 1 D 5 D 6 D 7 D 8 = 1 D 9 D 10 D 11 D 12 = 1 D 13 D 14 D 15

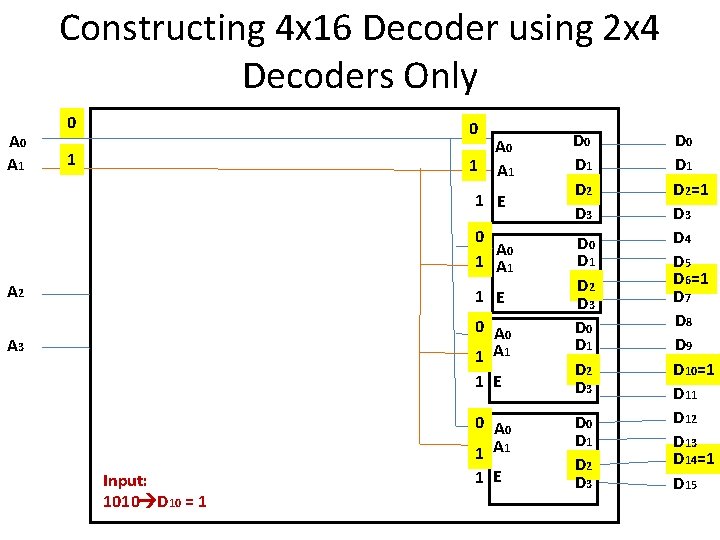
Constructing 4 x 16 Decoder using 2 x 4 Decoders Only A 0 A 1 0 0 A 0 1 A 1 1 1 E 0 A 0 1 A 1 D 0 D 1 D 2 D 3 A 2 1 E A 3 0 A 0 1 A 1 1 E D 0 D 1 D 2 D 3 Input: 1010 D 10 = 1 D 0 D 1 D 2=1 D 3 D 4 D 5 D 6=1 D 7 D 8 D 9 D 10=1 D 12 D 13 D 14=1 D 15

Constructing 4 x 16 Decoder using 2 x 4 Decoders Only A 0 A 1 0 0 D 0 A 2 A 3 D 0 A 1 2 x 4 D 1 D 2 E D 3 A 0 A 1 0 A 0 D 1 1 A 0 A 1 D 2 2 x 4 Decoder Input: 1000 D 8 = 1 E 2 x 4 E A 0 A 1 D 3 2 x 4 E 2 x 4 D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10 D 11 D 12 D 13 D 14 D 15

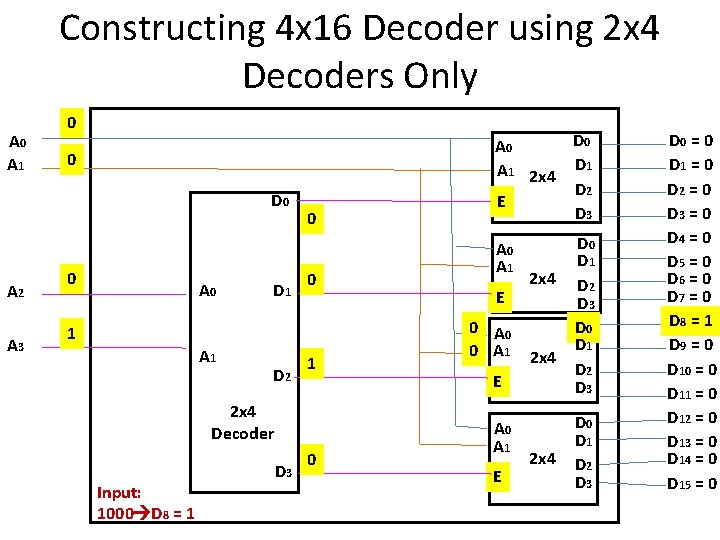
Constructing 4 x 16 Decoder using 2 x 4 Decoders Only A 0 A 1 0 0 D 0 A 2 A 3 0 A 0 D 1 0 0 1 A 1 D 2 1 2 x 4 Decoder Input: 1000 D 8 = 1 D 3 0 D 0 A 1 2 x 4 D 1 D 2 E D 3 A 0 A 1 E 0 A 0 0 A 1 2 x 4 E A 0 A 1 E 2 x 4 D 0 D 1 D 2 D 3 D 0 = 0 D 1 = 0 D 2 = 0 D 3 = 0 D 4 = 0 D 5 = 0 D 6 = 0 D 7 = 0 D 8 = 1 D 9 = 0 D 10 = 0 D 11 = 0 D 12 = 0 D 13 = 0 D 14 = 0 D 15 = 0

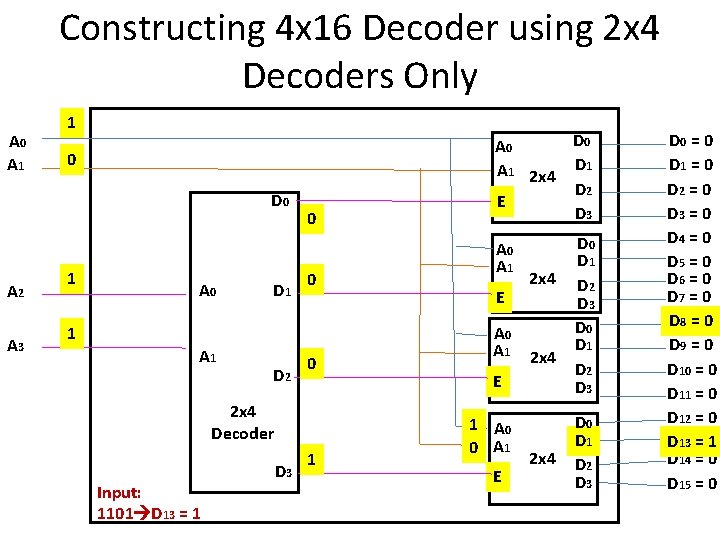
Constructing 4 x 16 Decoder using 2 x 4 Decoders Only A 0 A 1 1 0 D 0 A 2 A 3 1 A 0 D 1 0 0 1 A 1 D 2 0 2 x 4 Decoder Input: 1101 D 13 = 1 D 3 1 D 0 A 1 2 x 4 D 1 D 2 E D 3 A 0 A 1 E A 0 A 1 2 x 4 E 1 A 0 0 A 1 E 2 x 4 D 0 D 1 D 2 D 3 D 0 = 0 D 1 = 0 D 2 = 0 D 3 = 0 D 4 = 0 D 5 = 0 D 6 = 0 D 7 = 0 D 8 = 0 D 9 = 0 D 10 = 0 D 11 = 0 D 12 = 0 D 13 = 1 D 14 = 0 D 15 = 0

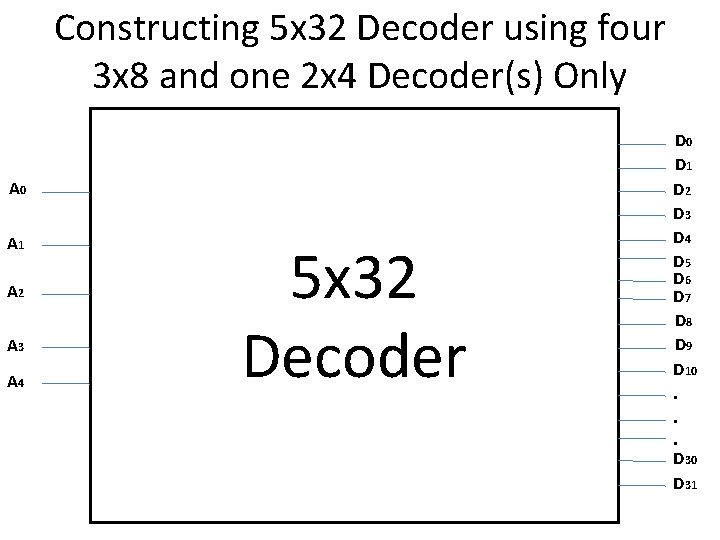
Constructing 5 x 32 Decoder using four 3 x 8 and one 2 x 4 Decoder(s) Only A 0 A 1 A 2 A 3 A 4 5 x 32 Decoder D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10. . . D 30 D 31

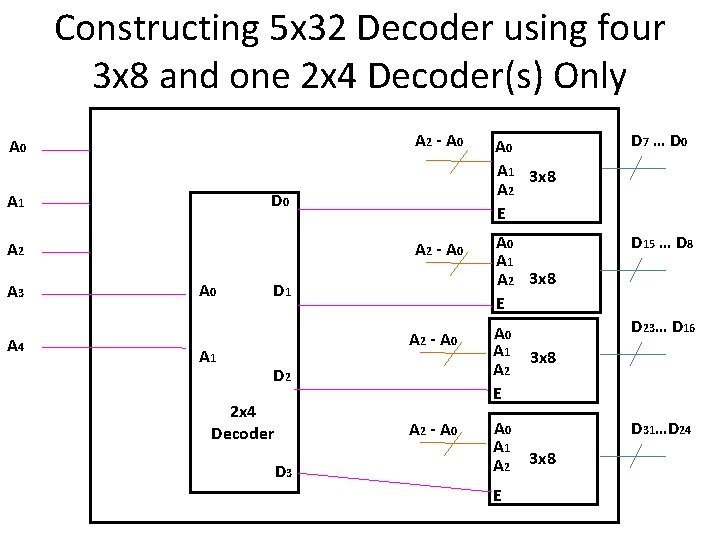
Constructing 5 x 32 Decoder using four 3 x 8 and one 2 x 4 Decoder(s) Only A 0 A 2 A 4 A 0 A 1 3 x 8 A 2 E D 7 … D 0 A 2 - A 0 A 1 A 2 3 x 8 E D 15 … D 8 A 2 - A 0 A 1 A 2 E D 23… D 16 A 2 - A 0 A 1 A 2 D 0 A 1 A 3 A 2 - A 0 A 1 D 2 2 x 4 Decoder D 3 E 3 x 8 D 31…D 24 3 x 8

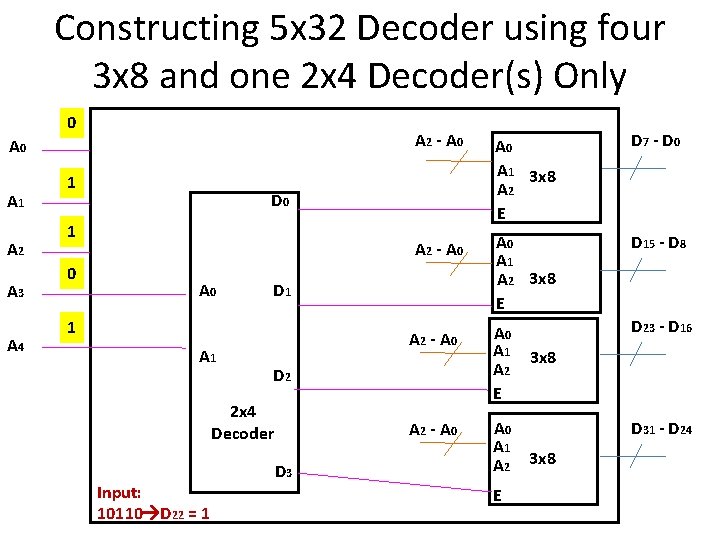
Constructing 5 x 32 Decoder using four 3 x 8 and one 2 x 4 Decoder(s) Only 0 A 1 A 2 A 3 A 4 1 A 0 A 1 3 x 8 A 2 E D 7 - D 0 A 2 - A 0 A 1 A 2 3 x 8 E D 15 - D 8 A 2 - A 0 A 1 A 2 E D 23 - D 16 A 2 - A 0 A 1 A 2 D 0 1 0 A 2 - A 0 D 1 1 A 1 D 2 2 x 4 Decoder Input: 10110 D 22 = 1 D 3 E 3 x 8 D 31 - D 24 3 x 8

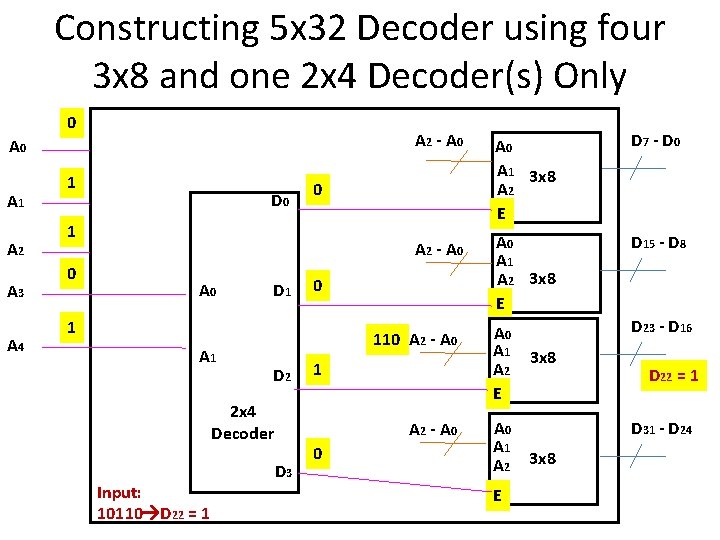
Constructing 5 x 32 Decoder using four 3 x 8 and one 2 x 4 Decoder(s) Only 0 A 1 A 2 A 3 A 4 1 D 0 A 0 D 1 A 2 - A 0 A 1 A 2 3 x 8 E D 15 - D 8 A 0 A 1 A 2 E D 23 - D 16 110 A 2 - A 0 D 2 2 x 4 Decoder Input: 10110 D 22 = 1 D 7 - D 0 0 1 A 0 A 1 3 x 8 A 2 E 0 1 0 A 2 - A 0 1 A 2 - A 0 D 3 0 A 1 A 2 E 3 x 8 D 22 = 1 D 31 - D 24 3 x 8

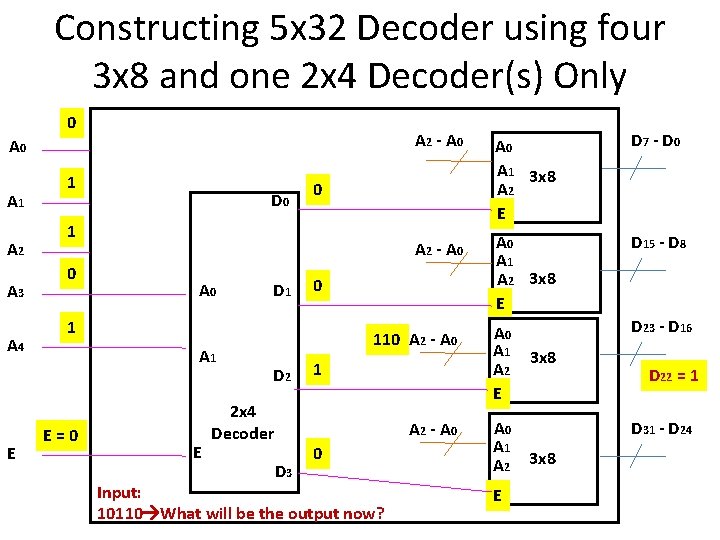
Constructing 5 x 32 Decoder using four 3 x 8 and one 2 x 4 Decoder(s) Only 0 A 1 A 2 A 3 A 4 E 1 D 0 A 0 D 1 E=0 E D 7 - D 0 A 2 - A 0 A 1 A 2 3 x 8 E D 15 - D 8 A 0 A 1 A 2 E D 23 - D 16 0 1 A 0 A 1 3 x 8 A 2 E 0 1 0 A 2 - A 0 110 A 2 - A 0 D 2 2 x 4 Decoder 1 A 2 - A 0 D 3 0 Input: 10110 What will be the output now? A 0 A 1 A 2 E 3 x 8 D 22 = 1 D 31 - D 24 3 x 8