Decision Theory Lecture 2 Decision Theory the foundation

Decision Theory – the foundation of modern economics • Individual decision making – under

• Individual decision making – under Certainty • Revealed preference and utility theory

• Individual decision making – under Certainty • Choice functions Weak axiom of

You go to a restaurant in while you are on vacation in Tuscany and

• Individual decision making – under Certainty • Revelead preference and ordinal utility

The doctrine of utilitarianism saw the maximization of utility as a moral criterion for

• Individual decision making – under Certainty • Operations Research, Management Science

• Individual decision making – under risk • Objective probabilities (Expected Utility) •

• Expected utility Theory – Cardinal utility function If u(. ) is a

Normative vs positive decision theory • Behavioral (positive) economics – Experiments – Psychology –

• Individual decision making – under uncertainty • Decision Rules (in a while)

Individual decision theory vs game theory

Zero‐sum games • In zero‐sum games, payoffs in each cell sum up to zero

Zero‐sum games • Minimax = maximin = value of the game • The game

Zero‐sum games • Or it may have no saddle points • To find the

Zero‐sum games • If there is more strategies, you don’t know which one will

Zero‐sum games • Column will try to choose x to minimize the upper envelope

Zero‐sum games • Tranform into Linear Programming

Fishing on Jamaica • In the fifties, Davenport studied a village of 200 people

• Twenty-six fishing crews in sailing, dugout canoes fish this area [fishing grounds

Strategies • There were 26 wooden canoes. The captains of the canoes might adopt

Advantages and disadvantages of fishing in the open sea Disadvantages • It takes more

Collecting data • Davenport collected the data concerning the fishermen average monthly profit depending

Zero‐sum game? The current’s problem • There is no saddle point • Mixed strategy:

Graphical solution of the current’s problem 21 19 17 15 Solution: p=0. 31 IN

The fishermen’s problem • Similarly: – For every fishermen’s strategy q 1, q 2

Maximin and minimax Maximize 13, 31 Fishers' mixed strategy q 1 q 2 q

Forecast and observation Game theory predicts Observation shows • No fishermen risks fishing outside

Current is not vicious • Kozelka 1969 and Read, Read 1970 pointed out a

Current may be vicious after all • The current does not reason, but it

Decision making under uncertainty FLOW NO FLOW MAXIMIN MAXIMAX MINIMAX REGRET 17, 3 11,

Decision making under uncertainty FishermenCurrent FLOW NO FLOW MAXIMIN MAXIMAX MINIMAX REGRET 17, 3

Decision making under uncertainty FishermenCurrent IN OUT IN‐OUT 0, 67 IN+0, 33 IN‐OUT FLOW

Father: “I want you to marry a girl of my choice” Son: “I will

Slides: 44

Download presentation

Decision Theory Lecture 2

Decision Theory – the foundation of modern economics • Individual decision making – under Certainty • Choice functions • Revelead preference and ordinal utility theory • Operations Research, Management Science – under Risk • • Expected Utility Theory (objective probabilities) Bayesian decision theory Prospect Theory and other behavioral theories Subjective Expected Utility (subjective probabilities) – under Uncertainty • Decision rules • Uncertainty aversion models • Interactive decision making – – • Non‐cooperative game theory Cooperative game theory Matching Bargaining Group decision making (Social choice theory) – Group decisions (Arrow, Maskin, etc. ) – Voting theory – Welfare functions

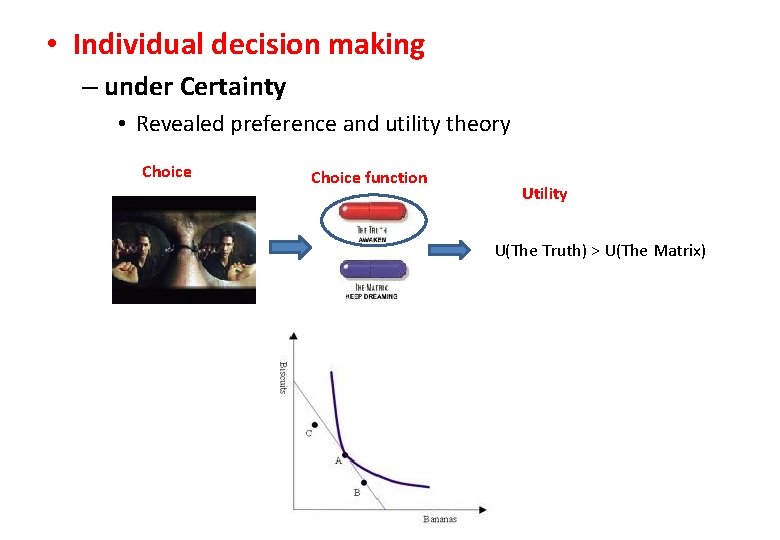
• Individual decision making – under Certainty • Revealed preference and utility theory Choice function Utility U(The Truth) > U(The Matrix)

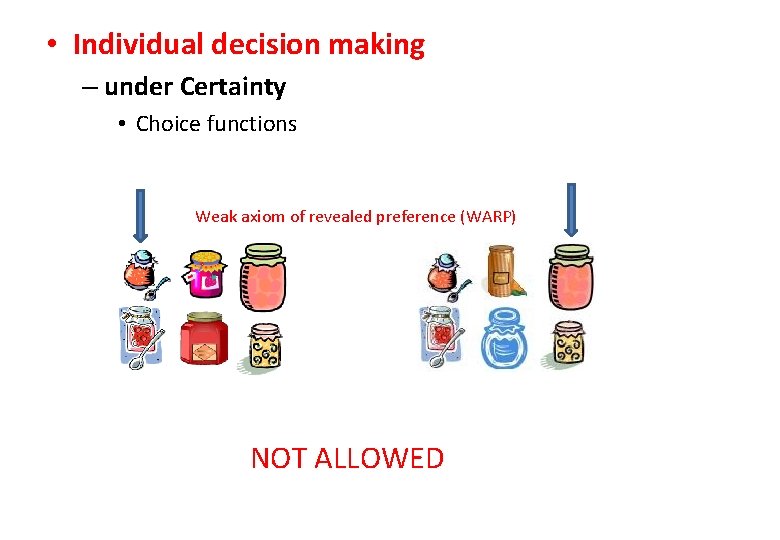
• Individual decision making – under Certainty • Choice functions Weak axiom of revealed preference (WARP) NOT ALLOWED

You go to a restaurant in while you are on vacation in Tuscany and you are given the following menu: • bistecca • pollo ? ? ? The cook anounces that he can also serve • trippa alla fiorentina

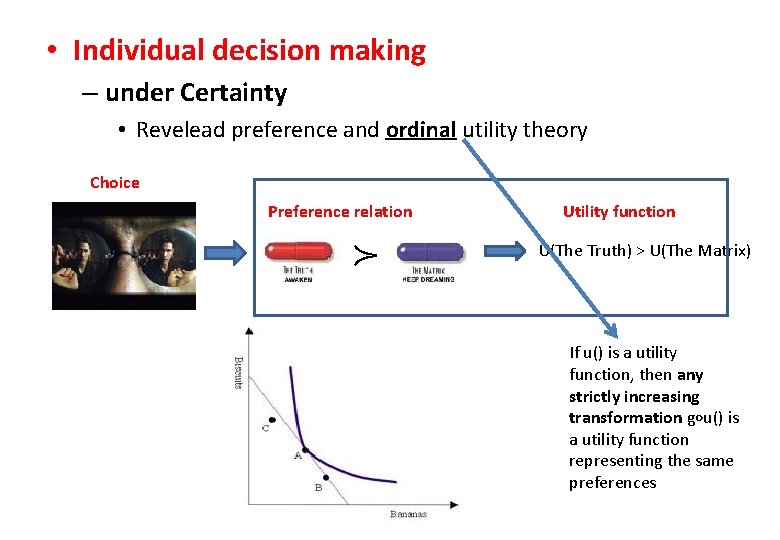
• Individual decision making – under Certainty • Revelead preference and ordinal utility theory Choice Preference relation ≻ Utility function U(The Truth) > U(The Matrix) If u() is a utility function, then any strictly increasing transformation g∘u() is a utility function representing the same preferences

The doctrine of utilitarianism saw the maximization of utility as a moral criterion for the organization of society. According to utilitarians, such as Jeremy Bentham (1748– 1832) and John Stuart Mill (1806– 1873), society should aim to maximize the total utility of individuals, aiming for "the greatest happiness for the greatest number of people". Another theory forwarded by John Rawls (1921– 2002) would have society maximize the utility of those with the lowest utility, raising them up to create a more equitable distribution across society

Choice function Preference relation ≻

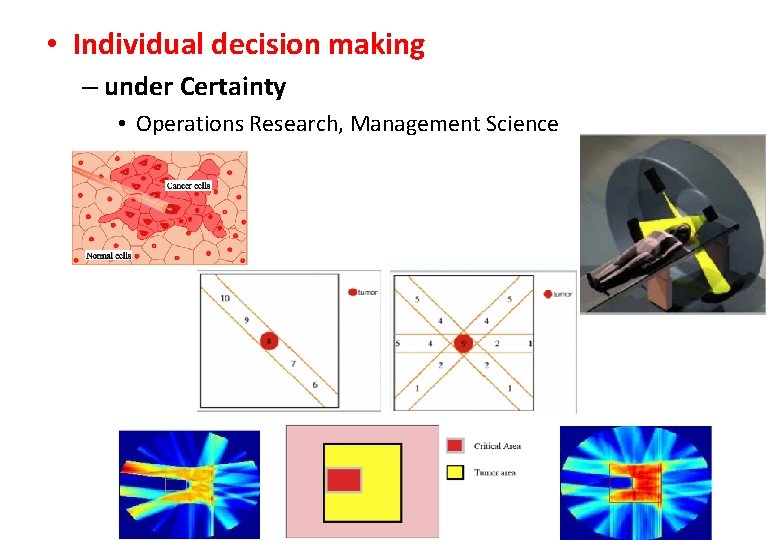
• Individual decision making – under Certainty • Operations Research, Management Science

• Individual decision making – under risk • Objective probabilities (Expected Utility) • Subjective probabilities (Subjective Expected Utility)

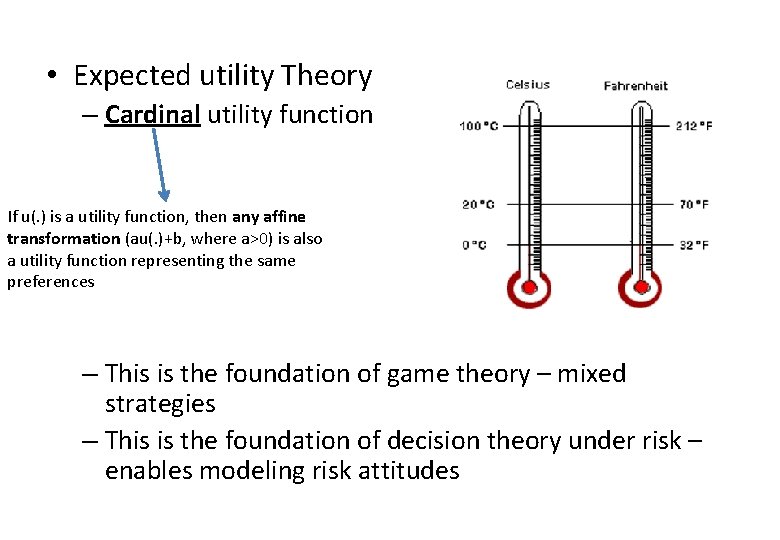
• Expected utility Theory – Cardinal utility function If u(. ) is a utility function, then any affine transformation (au(. )+b, where a>0) is also a utility function representing the same preferences – This is the foundation of game theory – mixed strategies – This is the foundation of decision theory under risk – enables modeling risk attitudes

Normative vs positive decision theory • Behavioral (positive) economics – Experiments – Psychology – Empirical results – Behavioral theories • Traditional (normative) economics – Mathematics – Traditional Macro and Micro

• Individual decision making – under uncertainty • Decision Rules (in a while) • Uncertainty/ambiguity aversion models, e. g. Multiple prior/maximin model of Gilboa, Schmeidler Subjective probability may not exist

Individual decision theory vs game theory

Zero‐sum games • In zero‐sum games, payoffs in each cell sum up to zero • Movement diagram

Zero‐sum games • Minimax = maximin = value of the game • The game may have multiple saddle points

Zero‐sum games • Or it may have no saddle points • To find the value of such game, consider mixed strategies

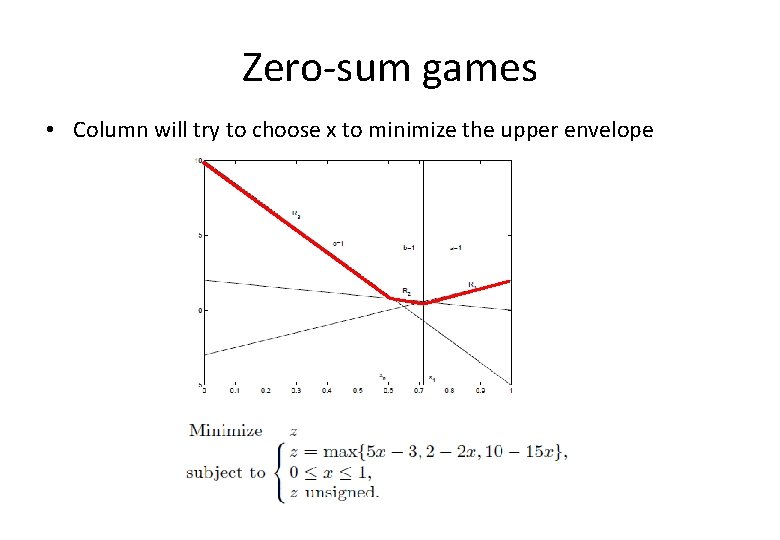
Zero‐sum games • If there is more strategies, you don’t know which one will be part of optimal mixed strategy. • Let Column mixed strategy be (x, 1‐x) • Then Raw will try to maximize

Zero‐sum games • Column will try to choose x to minimize the upper envelope

Zero‐sum games • Tranform into Linear Programming

Fishing on Jamaica • In the fifties, Davenport studied a village of 200 people on the south shore of Jamaica, whose inhabitants made their living by fishing.

• Twenty-six fishing crews in sailing, dugout canoes fish this area [fishing grounds extend outward from shore about 22 miles] by setting fish pots, which are drawn and reset, weather and sea permitting, on three regular fishing days each week … The fishing grounds are divided into inside and outside banks. The inside banks lie from 5 -15 miles offshore, while the outside banks all lie beyond … Because of special underwater contours and the location of one prominent headland, very strong currents set across the outside banks at frequent intervals … These currents are not related in any apparent way to weather and sea conditions of the local region. The inside banks are almost fully protected from the currents. [Davenport 1960]

Jamaica on a map

Strategies • There were 26 wooden canoes. The captains of the canoes might adopt 3 fishing strategies: – IN – put all pots on the inside banks – OUT – put all pots on the outside banks – IN-OUT) – put some pots on the inside banks, some pots on the outside

Advantages and disadvantages of fishing in the open sea Disadvantages • It takes more time to reach, so fewers pots can be set • When the current is running, it is harmful to outside pots – marks are dragged away – pots may be smashed while moving – changes in temeperature may kill fish inside the pots Advanatages • The outside banks produce higher quality fish both in variaties and in size. – If many outside fish are available, they may drive the inside fish off the market. • The OUT and IN‐OUT strategies require better canoes. – Their captains dominate the sport of canoe racing, which is prestigious and offers large rewards.

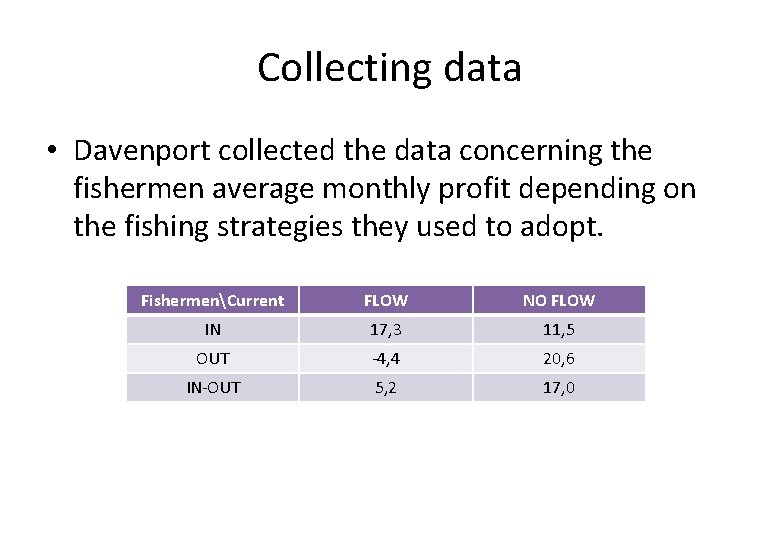
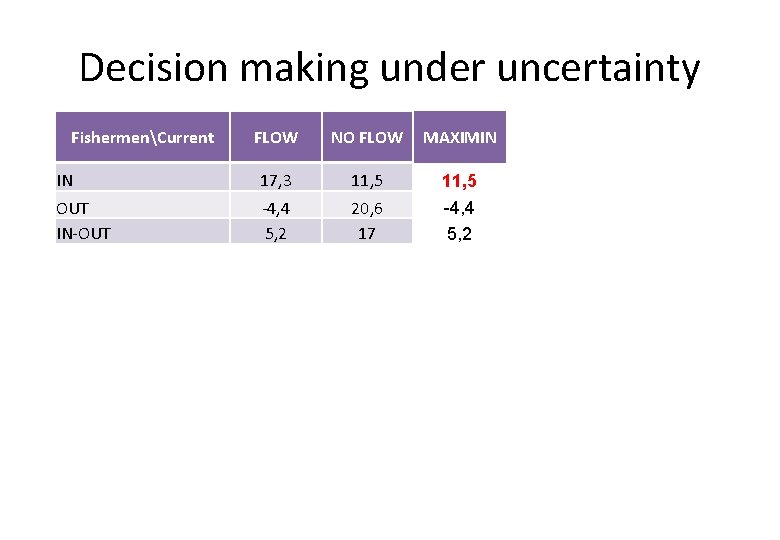
Collecting data • Davenport collected the data concerning the fishermen average monthly profit depending on the fishing strategies they used to adopt. FishermenCurrent FLOW NO FLOW IN 17, 3 11, 5 OUT ‐ 4, 4 20, 6 IN‐OUT 5, 2 17, 0

OUT Strategy

Zero‐sum game? The current’s problem • There is no saddle point • Mixed strategy: – Assume that the current is vicious and plays strategy FLOW with probability p, and NO FLOW with probability 1‐p – Fishermen’s strategy: IN with prob. q 1, OUT with prob. q 2, IN‐OUT with prob. q 3 – For every p, fishermen choose q 1, q 2 and q 3 that maximizes: – And the vicious current chooses p, so that the fishermen get min

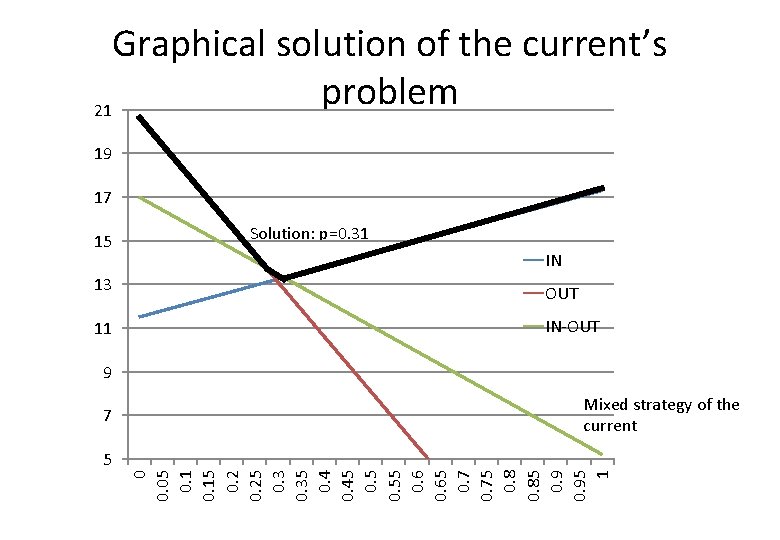
Graphical solution of the current’s problem 21 19 17 15 Solution: p=0. 31 IN 13 OUT 11 IN‐OUT 9 7 Mixed strategy of the current 0 0. 05 0. 15 0. 25 0. 35 0. 45 0. 55 0. 65 0. 75 0. 85 0. 95 1 5

The fishermen’s problem • Similarly: – For every fishermen’s strategy q 1, q 2 and q 3, the vicious current chooses p so that the fishermen earn the least: – The fishermen will try to choose q 1, q 2 and q 3 to maximize their payoff:

Maximin and minimax Maximize 13, 31 Fishers' mixed strategy q 1 q 2 q 3 0, 67 0, 00 0, 33 Expected payoff of the current when FLOW NO FLOW probabilities 13, 31 1, 00 >= >= = objective function Value of the game minimize Expected payoff from strategy: IN OUT IN_OUT probabilities objective function 13, 31 12, 79 13, 31 1, 00 Optimal strategy for the fishermen 13, 31 1, 00 Mixed strategy of the current p 1 -p 0, 31 0, 69 <= <= <= = 13, 31 1, 00 Optimal strategy for the current

Forecast and observation Game theory predicts Observation shows • No fishermen risks fishing outside • Strategy 67% IN, 33% IN-OUT [Payoff: 13. 31] • Optimal current’s strategy 31% FLOW, 69% NO FLOW • No fishermen risks fishing outside • Strategy 69% IN, 31% IN-OUT [Payoff: 13. 38] • Current’s „strategy”: 25% FLOW, 75% NO FLOW The similarity is striking Davenport’s finding went unchallenged for several years Until …

Current is not vicious • Kozelka 1969 and Read, Read 1970 pointed out a serious flaw: – The current is not a reasoning entity and cannot adjust to fishermen changing their strategies. – Hence fishermen should use Expected Value principle: • Expected payoff of the fishermen: – IN: 0. 25 x 17. 3 + 0. 75 x 11. 5 = 12. 95 – OUT: 0. 25 x (‐ 4. 4) + 0. 75 x 20. 6 = 14. 35 – IN‐OUT: 0. 25 x 5. 2 + 0. 75 x 17. 0 = 14. 05 • Hence, all of the fishermen should fish OUTside. • Maybe, they are not well adapted after all

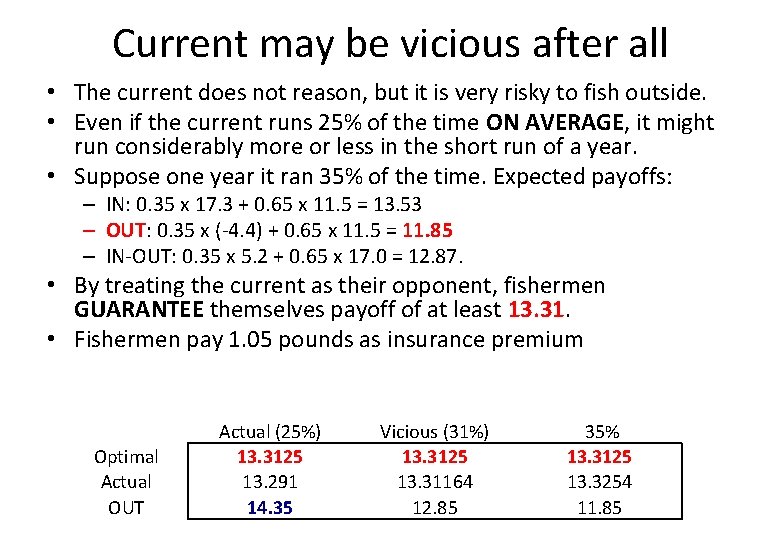
Current may be vicious after all • The current does not reason, but it is very risky to fish outside. • Even if the current runs 25% of the time ON AVERAGE, it might run considerably more or less in the short run of a year. • Suppose one year it ran 35% of the time. Expected payoffs: – IN: 0. 35 x 17. 3 + 0. 65 x 11. 5 = 13. 53 – OUT: 0. 35 x (‐ 4. 4) + 0. 65 x 11. 5 = 11. 85 – IN‐OUT: 0. 35 x 5. 2 + 0. 65 x 17. 0 = 12. 87. • By treating the current as their opponent, fishermen GUARANTEE themselves payoff of at least 13. 31. • Fishermen pay 1. 05 pounds as insurance premium Optimal Actual OUT Actual (25%) 13. 3125 13. 291 14. 35 Vicious (31%) 13. 3125 13. 31164 12. 85 35% 13. 3125 13. 3254 11. 85

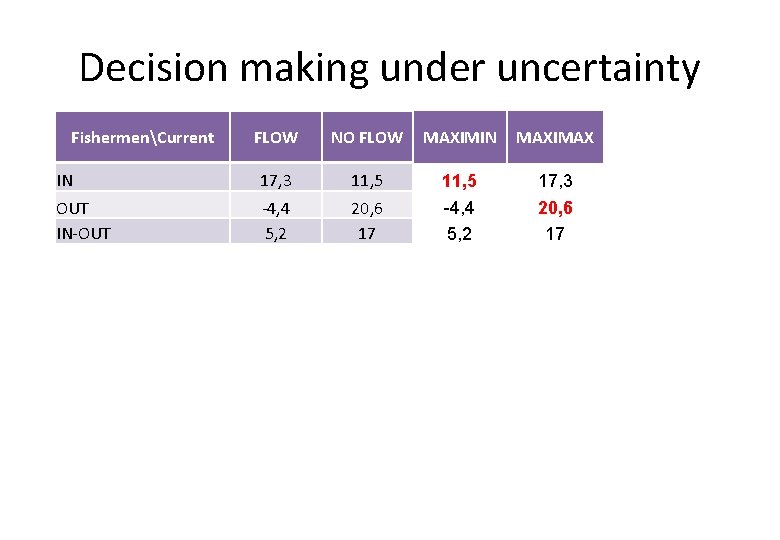
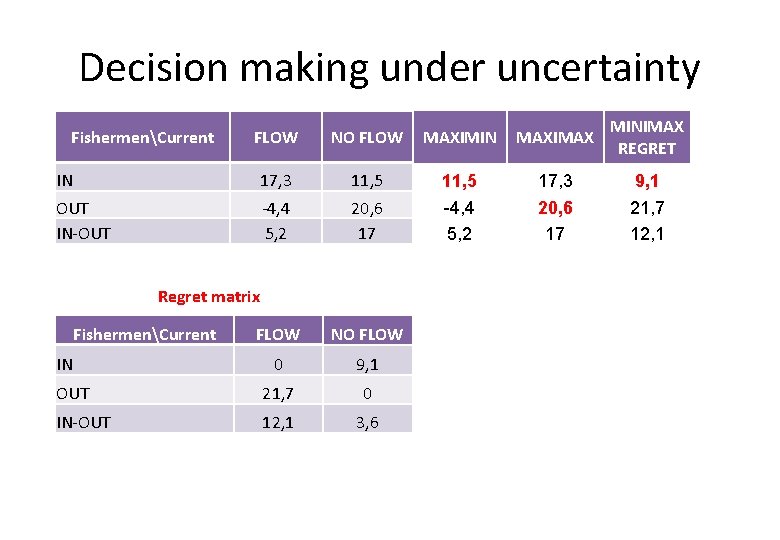
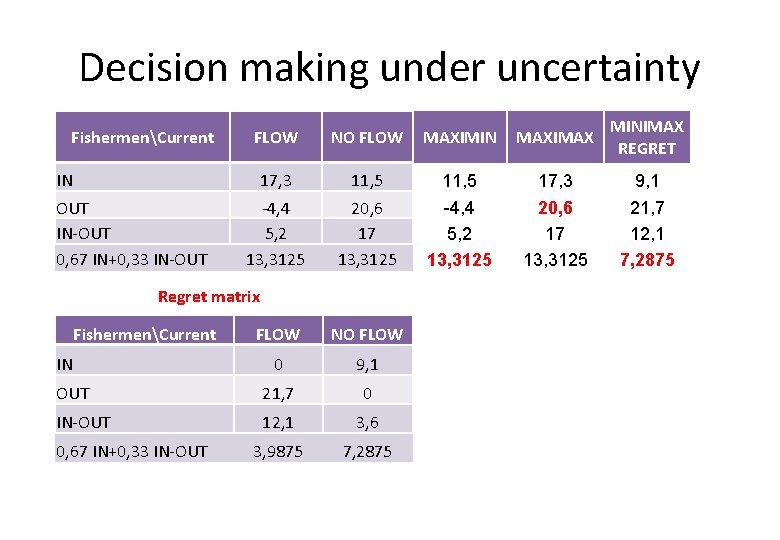
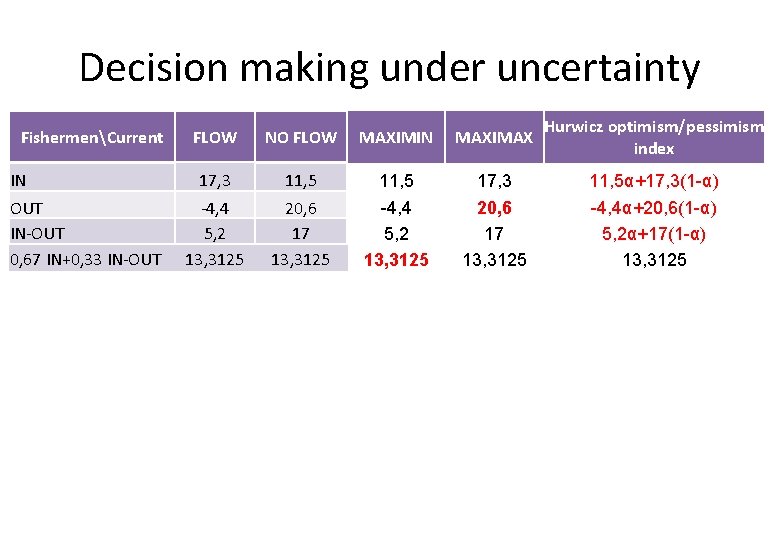
Decision making under uncertainty FLOW NO FLOW MAXIMIN MAXIMAX MINIMAX REGRET 17, 3 11, 5 17, 3 9, 1 ‐ 4, 4 5, 2 13, 3125 20, 6 17 13, 3125 -4, 4 5, 2 13, 3125 20, 6 17 13, 3125 21, 7 12, 1 7, 2875 Płynie Nie płynie 0 9, 1 OUT 21, 7 0 IN‐OUT 12, 1 3, 6 3, 9875 7, 2875 FishermenCurrent IN OUT IN‐OUT 0, 67 IN+0, 33 IN‐OUT RybacyPrąd IN 0, 67 IN+0, 33 IN‐OUT

Decision making under uncertainty FishermenCurrent FLOW NO FLOW MAXIMIN MAXIMAX MINIMAX REGRET 17, 3 11, 5 17, 3 9, 1 ‐ 4, 4 5, 2 13, 3125 20, 6 17 13, 3125 -4, 4 5, 2 13, 3125 20, 6 17 13, 3125 21, 7 12, 1 7, 2875 IN OUT IN‐OUT 0, 67 IN+0, 33 IN‐OUT Regret matrix FishermenCurrent FLOW NO FLOW 0 9, 1 OUT 21, 7 0 IN‐OUT 12, 1 3, 6 3, 9875 7, 2875 IN 0, 67 IN+0, 33 IN‐OUT

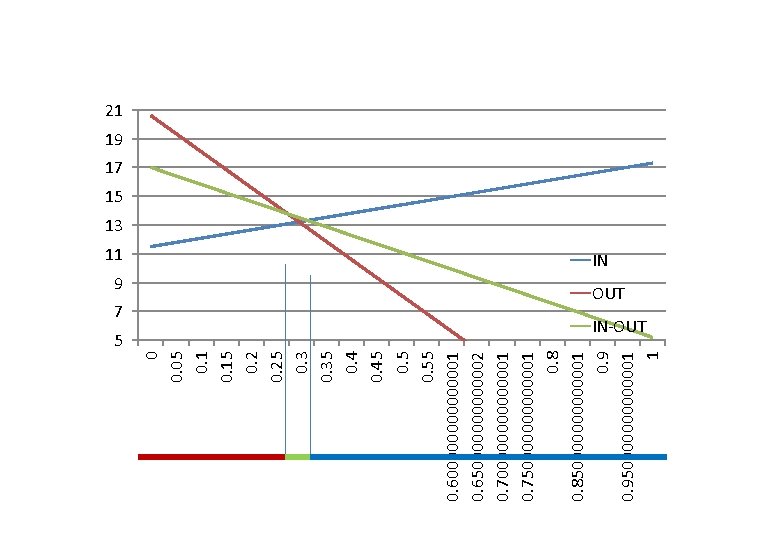
Decision making under uncertainty FishermenCurrent IN OUT IN‐OUT 0, 67 IN+0, 33 IN‐OUT FLOW NO FLOW MAXIMIN MAXIMAX Hurwicz optimism/pessimism index 17, 3 11, 5α+17, 3(1 -α) ‐ 4, 4 5, 2 13, 3125 20, 6 17 13, 3125 -4, 4α+20, 6(1 -α) 5, 2α+17(1 -α) 13, 3125

11 9 7 5 0 0. 05 0. 15 0. 25 0. 35 0. 45 0. 55 0. 600000001 0. 650000002 0. 700000001 0. 750000001 0. 850000001 0. 950000001 1 21 19 17 15 13 IN OUT IN‐OUT

Father: “I want you to marry a girl of my choice” Son: “I will choose my own bride!” Father: “But the girl is Bill Gates’ daughter. ” Son: “Well, in that case…ok” Next, the father approaches Bill Gates. Father: “I have a husband for your daughter. ” Bill Gates: “But my daughter is too young to marry!” Father: “But this young man is a vice‐president of the World Bank. ” Bill Gates: “Ah, in that case…ok” Finally the father goes to see the president of the World Bank. Father: “I have a young man to be recommended as a vicepresident. ” President: “But I already have more vice‐ presidents than I need!” Father: “But this young man is Bill Gates’s son‐in‐law. ” President: “Ah, in that case…”