Decision Procedures An Algorithmic Point of View Basic

Decision Procedures An Algorithmic Point of View Basic Concepts and Background Daniel Kroening and Ofer Strichman 1

Outline n What is Logic n Proofs by deduction n Proofs by enumeration n Decidability, soundness and completeness n Some notes on Propositional Logic Decision Procedures An algorithmic point of view 2

What is Logic? n Some useful definitions on the web: ¨ “science dealing with the principles of valid reasoning and argument” ¨ “A formal and powerful method of explaining why the program doesn't work” ¨ “The art of being wrong with confidence” Decision Procedures An algorithmic point of view 3

So what is Logic? n Defined by ¨ Syntax (including the Signature of the logic : variables and their domain, function and predicate symbols, quantifiers, etc) ¨ Axioms and n Inference rules. A logic allows us to infer theorems. Decision Procedures An algorithmic point of view 4

Example: Propositional Logic n Syntax formula: Boolean-var | : formula | formula Ç formula | ( formula ) | T | F (Can also use: formula Æ formula | formula ! formula…) n Axioms: 1. 2. 3. n ` (A ! (B ! A)) ` ((A ! (B ! C)) ! ((A ! B) ! (A ! C))) ` (: B ! : A) ! (A ! B) Inference Rule: Modus Ponens (MP) `A A specific (one of many possible) Deductive System for Propositional Logic. It is known as the Hilbert System H. `A!B `B Decision Procedures An algorithmic point of view 5

A proof by deduction: example n Notation: `H ‘there exists a proof of in H’ n Theorem: `H (A ! B) ! ((B ! C) ! (A ! C)) 1. {A ! B, B ! C, A} `H A Premise 2. {A ! B, B ! C, A} `H A ! B Premise 3. {A ! B, B ! C, A} `H B M. P. 1, 2 4. {A ! B, B ! C, A} `H B ! C Premise 5. {A ! B, B ! C, A} `H C M. P. 3, 4 6. {A ! B, B ! C} Deduction 5 7. {A ! B} `H ((B ! C) ! (A ! C)) 8. `H (A ! C) `H (A ! B) ! ((B ! C) ! (A ! C)) Decision Procedures An algorithmic point of view Deduction 6 Deduction 7 6

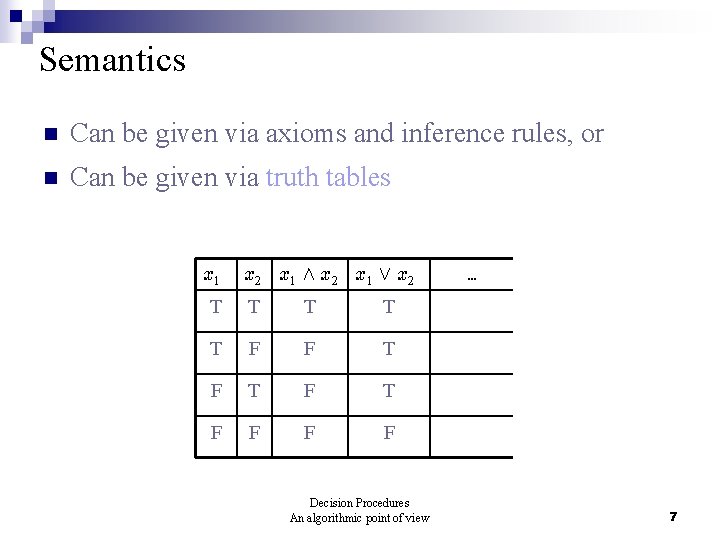
Semantics n Can be given via axioms and inference rules, or n Can be given via truth tables x 1 x 2 x 1 Æ x 2 x 1 Ç x 2 T T T F F T F T F F Decision Procedures An algorithmic point of view . . . 7

Satisfying interpretations n If an assignment satisfies (according to the truth tables) a formula , we write: ² . n Example: : : (x 1 Æ : (x 2 Ç : x 3)) ¨ 1: (x 1 = T, x 2 = F, x 3 = F) 1 ² ¨ 2: (x 1 = T, x 2 = F, x 3 = T) 2 2 Decision Procedures An algorithmic point of view 8

Satisfiability, Validity, etc. n Definition (Satisfiability): A formula is satisfiable if 9. ² n Definition (Validity): A formula is valid if 8. ² . If is valid, we write ². n Observation: is valid if and only if : is unsatisfiable. Decision Procedures An algorithmic point of view 9

A proof by enumeration: same example A T T T B T T F C (A ! B) ! ((B ! C) ! (A ! C)) T T F F F T T F F F T F ² T T T (A ! B) ! ((B ! C) ! (A ! C)) Decision Procedures An algorithmic point of view 10

Soundness and completeness of a deductive system n Given a deductive system D, ¨ D is sound for a logic L, if for every formula f in L, `D f ! ² f ¨ D is complete if for every formula f in L, ² f ! `D f Decision Procedures An algorithmic point of view 11

The decision problem n Definition (the decision problem): The decision problem for a formula: given , is valid? n Definition (decision Procedure for a logic): A decision procedure for a logic is an algorithm that solves the decision problem for any formula in this logic. n We are naturally interested in a sound and complete decision procedure. Decision Procedures An algorithmic point of view 12

Soundness and Completeness n What does it mean that a decision procedure is sound and complete? ¨ Soundness: the answer returned by the decision procedure is always correct (Question: ‘correct’ according to what? ) ¨ Completeness: returns with a yes/no answer in finite time. (Question: How does this definition relate to the definition of completeness of a deduction system? ) Decision Procedures An algorithmic point of view 13

Soundness and Completeness n Soundness: “when I say that it rains, and when I say it doesn’t rain, it doesn’t rain” n Completeness: “If asked, I always reply (in a finite time…) whether it rains” n A logic is decidable there is a sound and complete algorithm that decides if a well-formed expression in this logic is valid. Decision Procedures An algorithmic point of view 14

Soundness and Completeness (cont’d) n Algorithm #1: for checking if it rains outside: “stand right outside the door and say ‘it rains’” n It is not sound because you might say it rains when it doesn’t. n But it is complete: you always get an answer in a finite time. Decision Procedures An algorithmic point of view 15

Soundness and Completeness (cont’d) n Algorithm #2 for checking if it rains outside: “stand right outside the door and say ‘it rains’ if and only if you feel the rain” n It is sound because you say it rains only if it actually rains. n It is incomplete because you do not say anything if it doesn’t rain (we do not know whether it doesn’t rain, or it takes the person too long to answer…). Decision Procedures An algorithmic point of view 16

Decidability n Propositional logic is decidable there is a sound and complete algorithm (e. g. , truth tables) to decide whether a propositional formula is valid. n Arithmetic over integers is undecidable (this is Gödel's incompleteness result) Decision Procedures An algorithmic point of view 17

Inference engines n We saw that in Propositional Logic we can infer with both a deductive system (“deduction”) and truth tables (“enumeration”). n Which, in the general case, is the better method? n All logics have a deductive definition. n NOT all logics can be decided with an enumerative method. Decision Procedures An algorithmic point of view 18

Enumerative methods Deductive methods “Truths tables” Axioms and Inference rules Or Requires thinking… Requires pressing ‘Enter’… Whenever we can: build an engine to think for us Decision Procedures An algorithmic point of view 19

Expressiveness of a logic n Each formula defines a language: the set of satisfying assignments (‘models’) are the words accepted by this language. n Consider the logic ‘ 2 -CNF’ formula : literal: ( literal Ç literal ) | formula Æ formula Boolean-variable | : Boolean-variable (x 1 Ç : x 2) Æ (: x 3 Ç x 2) Decision Procedures An algorithmic point of view 20

Expressiveness of a logic n Now consider a Propositional Logic formula : (x 1 Ç x 2 Ç x 3). n Q: Can we express this language with 2 -CNF? n A: No. Proof: language accepted by has 7 words: all assignments other than x 1 = x 2 = x 3 = F. ¨ The first 2 -CNF clause removes ¼ of the assignments, which leaves us with 6 accepted words. Additional clauses only remove more assignments. Decision Procedures An algorithmic point of view 21

Expressiveness of a logic Languages defined by L 2 is more expressive than L 1. Denote: L 1 Á L 2 Languages defined by L 1 n Claim: 2 -CNF Á Propositional Logic n Generally there is only a partial order between logics. Decision Procedures An algorithmic point of view 22

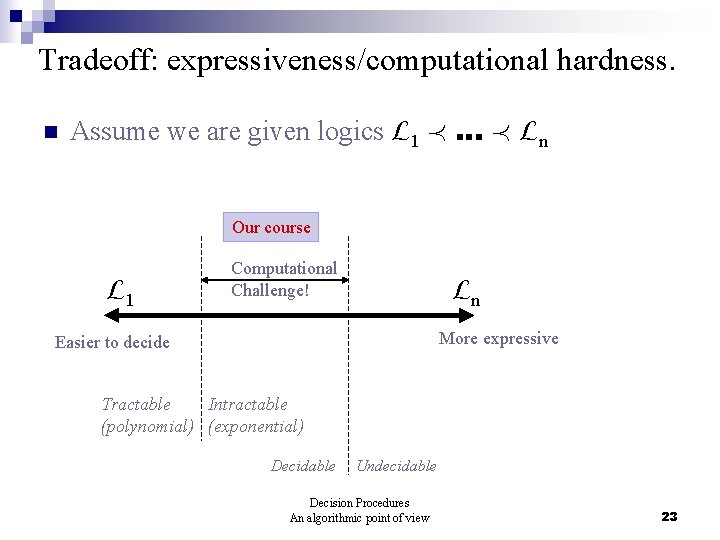
Tradeoff: expressiveness/computational hardness. n Assume we are given logics L 1 Á … Á Ln Our course L 1 Computational Challenge! Ln More expressive Easier to decide Tractable Intractable (polynomial) (exponential) Decidable Undecidable Decision Procedures An algorithmic point of view 23

When is a specific logic useful? 1. Expressible enough to state something interesting. 2. Decidable (or semi-decidable) and more efficiently solvable than richer logics. 3. More expressible, or more natural for expressing some models in comparison to ‘leaner’ logics. Decision Procedures An algorithmic point of view 24

Example: First Order Peano Arithmetic n constants: 0, 1 n Function symbols: ‘+’, ‘*’, Predicate symbol: ‘=’ n Domain: Natural numbers n Axioms (“semantics”): 1. 2. + * 3. 4. 5. 6. 7. 8 x : (0 x + 1) 8 x : 8 y : (x y) ! (x + 1 y + 1) Induction 8 x: x+0=x 8 x : 8 y : (x + y) + 1 = x + (y + 1) 8 x: x*0=0 8 x 8 y : x * (y + 1) = x * y + x Decision Procedures An algorithmic point of view Undecidable! These axioms define the semantics of ‘+’ 25

Example: Presburger Arithmetic n constants: 0, 1 n Function symbols: ‘+’, ‘*’, Predicate symbol: ‘=’ n Domain: Natural numbers n Axioms (“semantics”): 1. 2. + * 3. 4. 5. 6. 7. Decidable! 8 x : (0 x + 1) 8 x : 8 y : (x y) ! (x + 1 y + 1) Induction 8 x: x+0=x 8 x : 8 y : (x + y) + 1 = x + (y + 1) 8 x: x*0=0 8 x 8 y : x * (y + 1) = x * y + x Decision Procedures An algorithmic point of view 26

Logic in Computer Science n Reasoning in AI n Proofs in verification n Queries in Databases n … many more Decision Procedures An algorithmic point of view 27

Some notes on Propositional Logic n The simplest of them all n NP-complete n Exceptionally efficient solvers (SAT engines, BDDs) n Formulas with 105 variables are being solved regularly n All the logics that we will consider can be reduced directly to this logic Decision Procedures An algorithmic point of view 28

Some notes on Propositional Logic n A literal: : v v positive literal negative literal n Also known as ‘the phase’, or ‘the polarity’ of the literal. n The “logical phase” of a literal can be computed by counting the number of negations that nest it: ¨v is logically negative in: : v, : (: (: v)), v ! u, : (u ! v) ¨v is logically positive in: v, : (v ! u) Decision Procedures An algorithmic point of view 29

Some notes on Propositional Logic n Normal forms: ¨ Conjunctive Normal Form (CNF) ¨ Disjunctive Normal Form (DNF) (for which satisfiability is in P) ¨ Negation Normal Form (NNF) (all negations are over literals, not sub formulas) CNF and DNF are special cases of NNF Decision Procedures An algorithmic point of view 30

Some notes on Propositional Logic n Checking Satisfiability of a Boolean formula : ¨ Convert to a CNF: with additional variables, in P time. ¨ Convert to DNF: Exp time and space ¨ Convert to NNF: P time Decision Procedures An algorithmic point of view 31

The ‘Pure literal rule’ n : (x Ç y) Æ (: x Ç z) Æ (x Ç y Ç : z) n y is ‘pure’: it only appears in one phase n Idea: when trying to satisfy , first assign y = true. n Why? If there is a satisfying assignment to , there is a satisfying assignment in which y = true. n Generalization: assign all pure literals according to their phase. Decision Procedures An algorithmic point of view 32

Pure literals in NNF n CNF is a special case of NNF n A pure literal is defined in the same way: a literal that only appears in one phase. n We can always start satisfiability checking by assigning these pure literals true or false according to their phase. n We will rely on a similar principle also when considering other Logics. Decision Procedures An algorithmic point of view 33

Monotonicity of NNF n Thm: NNF formulas are monotonically satisfied (in CNF this is simply the pure literal rule) Satisfied literals ’: 1 : 0 ² ! ’ ² ’ 1 0 1 1 0 : (x 1 Æ : x 2) Ç (x 2 Ç (x 3 Æ x 1)) Decision Procedures An algorithmic point of view 34

Monotonicity of NNF (example) n : (: x Æ y) Ç z : (x, y, z) = (0, 1, 0) ² S={: x, y} ’ : (x, y, z) = (0, 1, 1) ’ ² S’={: x, y, z} Decision Procedures An algorithmic point of view 35

Some notes… n Why is monotonicity relevant to our decision procedures ? n We will use the fact that if we make unsatisfied predicates satisfied, we do not make the formula unsatisfied. n We will rely heavily on this fact later: it simplifies decision procedures. Decision Procedures An algorithmic point of view 36