Decision Making via Linear Programming A simple introduction

The nature of simple LP • One, single decision criterion – Either maximize or

Introducing LP via example • Suppose we manufacture furniture. • We must decide how

Obviously we can’t make an infinite number of tables or chairs. • Each table

Let’s write all this in algebraic form • Let x 1 be how many

Because your professor cleverly drew an example with only two variables x 1 and

The best (“optimal”) solution is always at a vertex! (Graph and solution generated by

Another site will solve problems with many variables. • http: //www. zweigmedia. com/Real. World/simplex.

Now let’s see how to solve these using Excel • You need the “Solver”

Now you try it. Set up this model, and solve it in Excel. A

Slides: 10

Download presentation

Decision Making via Linear Programming: A simple introduction Fred Phillips fred. phillips@stonybrook. edu

The nature of simple LP • One, single decision criterion – Either maximize or minimize something – Usually, profit or cost • No consideration of probability • Usually one best answer • Elaborations of LP allow for probabilities, multiple criteria, integer-only solutions, and more. – We’ll look at some of these elaborations later in the semester.

Introducing LP via example • Suppose we manufacture furniture. • We must decide how many tables and how many chairs to make this week. • We assume we can sell all that we make. – At a profit of $4/table and $3/chair.

Obviously we can’t make an infinite number of tables or chairs. • Each table requires 4 hours processing in machine (or ‘department’) A. . . –. . . and 2 hours in machine (dept. ) B. • Each chair requires 2 hours in dept. A. . . –. . . and 4 hours in B. • We have capacity constraints: – A total of 60 hours/week in dept. A, and – A total of 48 hours/week in dept. B.

Let’s write all this in algebraic form • Let x 1 be how many tables we make. • Let x 2 be how many chairs we make. • We want to maximize 4 x 1 + 3 x 2 • Subject to our capacity constraints: 4 x 1 + 2 x 2 < 60 2 x 1 + 4 x 2 < 48 • We also require that x 1 > 0 and x 2 > 0

Because your professor cleverly drew an example with only two variables x 1 and x 2, • We can solve the exercise using a 2 D graph. • This is not possible for realistic problems which may have several thousand variables.

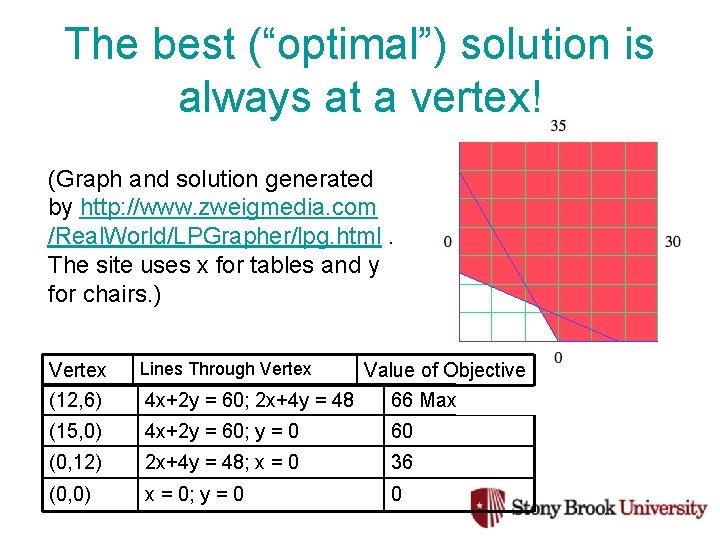
The best (“optimal”) solution is always at a vertex! (Graph and solution generated by http: //www. zweigmedia. com /Real. World/LPGrapher/lpg. html. The site uses x for tables and y for chairs. ) Vertex (12, 6) Lines Through Vertex (15, 0) 4 x+2 y = 60; y = 0 60 (0, 12) 2 x+4 y = 48; x = 0 36 (0, 0) x = 0; y = 0 0 Value of Objective 4 x+2 y = 60; 2 x+4 y = 48 66 Maximum

Another site will solve problems with many variables. • http: //www. zweigmedia. com/Real. World/simplex. html

Now let’s see how to solve these using Excel • You need the “Solver” plug-in. • Watch http: //www. youtube. com/watch? v=0 KPH myyghew

Now you try it. Set up this model, and solve it in Excel. A customer of the Regal Corporation needs 1, 000 pounds of a chemical mixture consisting of three raw materials. Cost for each of these is as follows: • X 1 = $2 per pound • X 2 = $3 per pound • X 3 = $4 per pound The customer requires the mixture to meet these conditions: • The mix must contain at least 200 pounds of X 2. • The mix cannot contain more than 400 pounds of X 1. • The mix must contain at least 100 pounds of X 3. Determine the least-cost mixture for the batch of 1, 000 pounds which will satisfy the customer's requirements.