Decision Diagrams for Discrete Optimization David Bergman School

Decision Diagrams for Discrete Optimization David Bergman School of Business, University of Connecticut Andre A. Cire, J. N. Hooker, Willem-Jan van Hoeve Tepper School of Business, Carnegie Mellon University 10/31/2020 1

Motivation • Traditional methods for discrete optimization rely on branch-andbound algorithms, applied to integer programming (IP) formulations • LP relaxations play a central role • Relaxation bounds • Feasible solutions • Branching • We propose a novel branch-and-bound algorithm for discrete optimization • Decision diagrams play a central role • Relaxation bounds – Relaxed BDDs • Feasible solutions – Restricted BDDs • Branching – Nodes of relaxed BDDs 10/31/2020 2

Motivation • Attractiveness of the approach • Richer modeling language • Dynamic Programming (DP) model • No need for inequality formulation • No need for integer variables • No need for linearlization • IP models may be too large to load into modern-day solvers • Exploit recursive structure of a problem • Much like traditional IP techniques exploit polyhedral structure through cutting-planes • Fast computation of bounds • Time devoted to creating relaxation controlled by user • More time and memory, better bound • Novel branching scheme • Several value assignments to variables • Eliminates symmetry 10/31/2020 3

Outline • Applications • Exact decision diagrams • Approximate decision diagrams • The branch-and-bound algorithm • Computational results 10/31/2020 4

Outline • Applications • Exact decision diagrams • Approximate decision diagrams • The branch-and-bound algorithm • Computational results 10/31/2020 5
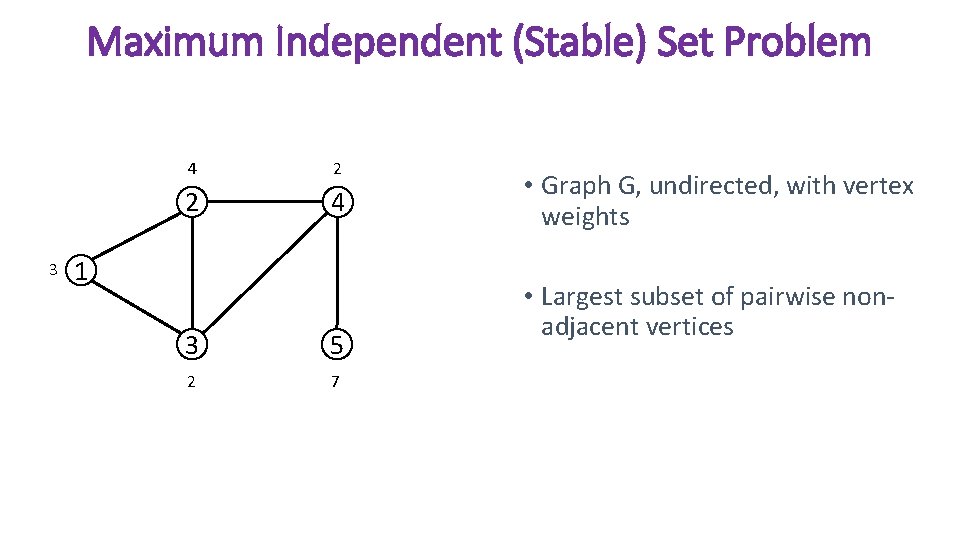
Maximum Independent (Stable) Set Problem 3 4 2 2 4 1 3 5 2 7 • Graph G, undirected, with vertex weights • Largest subset of pairwise nonadjacent vertices
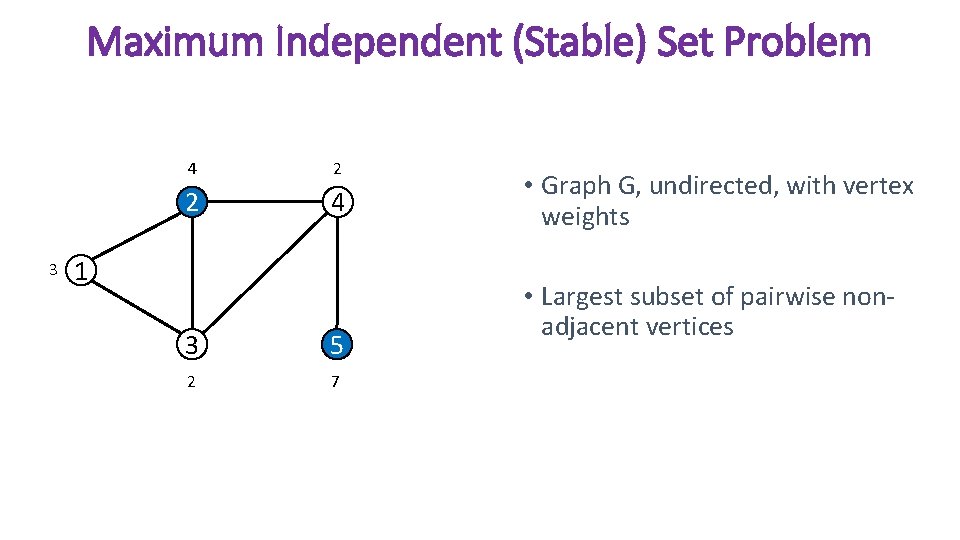
Maximum Independent (Stable) Set Problem 3 4 2 2 4 1 3 5 2 7 • Graph G, undirected, with vertex weights • Largest subset of pairwise nonadjacent vertices

Maximum Independent (Stable) Set Problem • Applications: • Biology • Protein structure alignment • Drug discovery • Social network analysis • Community detection • Coding theory • Computing maximum number of words, each at least a certain hamming distance away • Geometry • Tiling conjecture – generalizing a theorem by Minkowski • Map labeling • Side problem in many theoretical computer science applications • Vertex Separator Problem • Vertex Coloring • Equivalent to maximum clique problem on the complement of the graph 10/31/2020 8
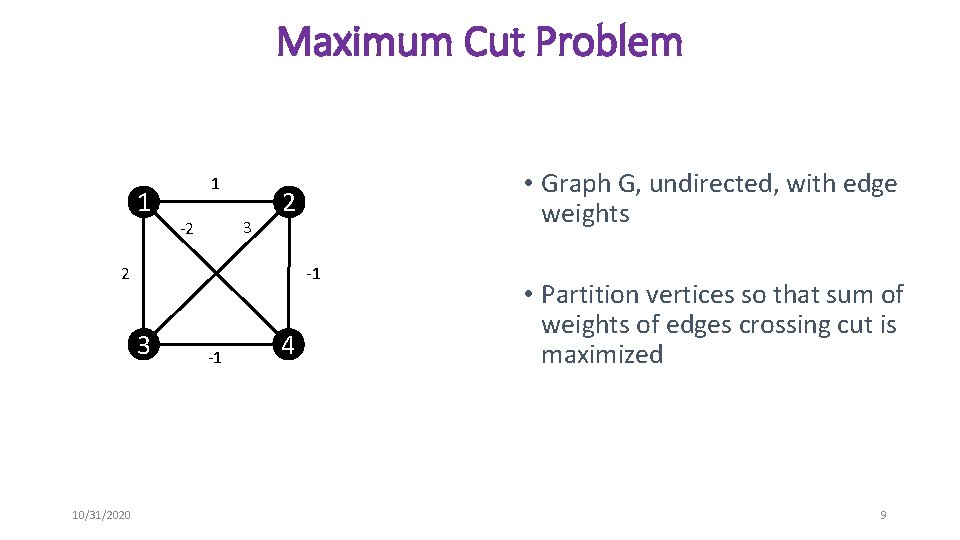
Maximum Cut Problem 1 1 3 -2 2 2 -1 3 10/31/2020 • Graph G, undirected, with edge weights -1 4 • Partition vertices so that sum of weights of edges crossing cut is maximized 9
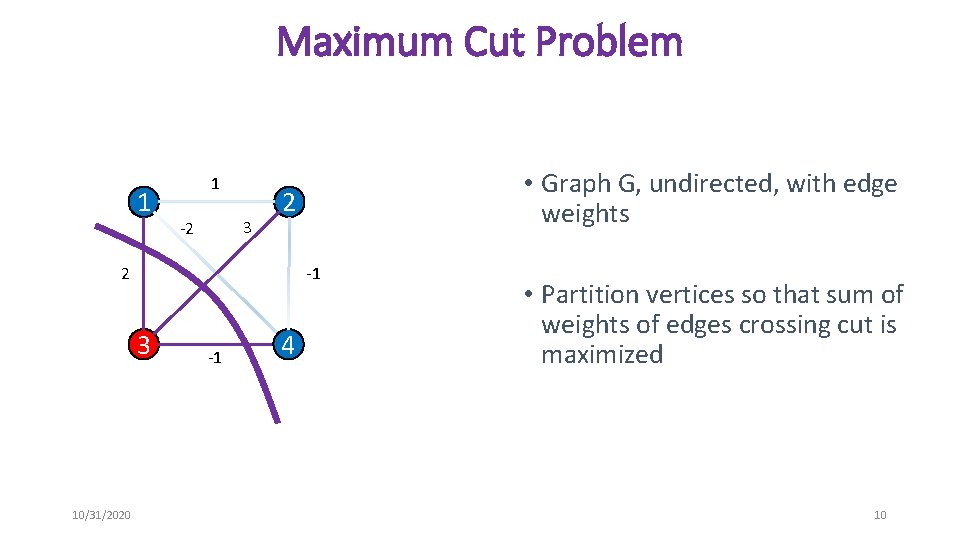
Maximum Cut Problem 1 1 3 -2 2 2 -1 3 10/31/2020 • Graph G, undirected, with edge weights -1 4 • Partition vertices so that sum of weights of edges crossing cut is maximized 10

Maximum Cut Problem • Applications: • VLSI design • Very-large-scale integration – process of creating integrated chips by combining thousands of transistors into a single chip • Vertical interconnection area • Statistical physics • Used to calculate ground state spin glasses with exterior magnetic fields • Data mining • Partitioning algorithms • Highly studied in theoretical computer science 10/31/2020 11

Outline • Applications • Exact decision diagrams • Approximate decision diagrams • The branch-and-bound algorithm • Computational results 10/31/2020 15

Decision Diagrams • Used to represent solutions to optimization problems • Solutions correspond to paths • Length of a path is the value of the objective function value of the solution it represents • They are compact representations of the entire search tree 10/31/2020 16
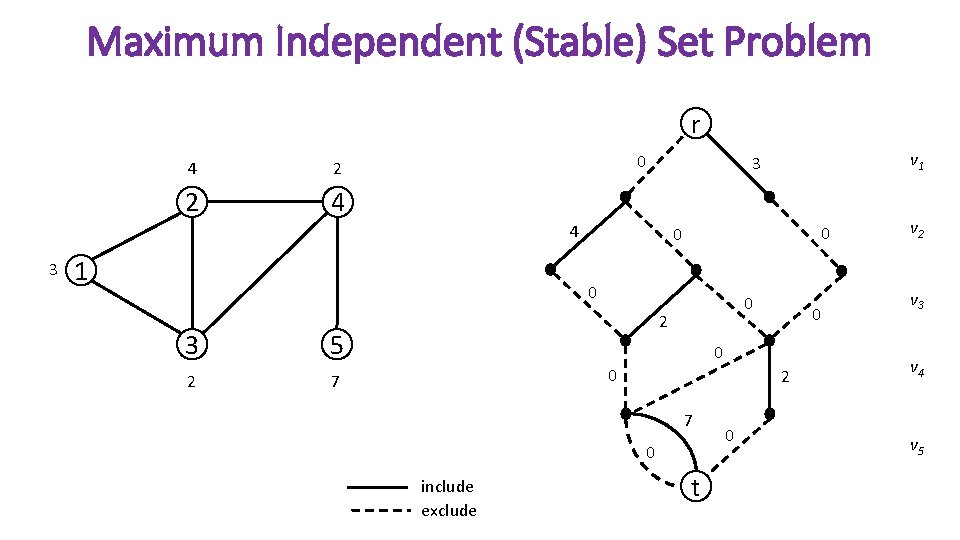
Maximum Independent (Stable) Set Problem r 4 2 2 4 0 4 3 1 0 0 0 3 5 2 7 v 1 3 0 2 0 0 0 2 7 0 include exclude t 0 v 2 v 3 v 4 v 5
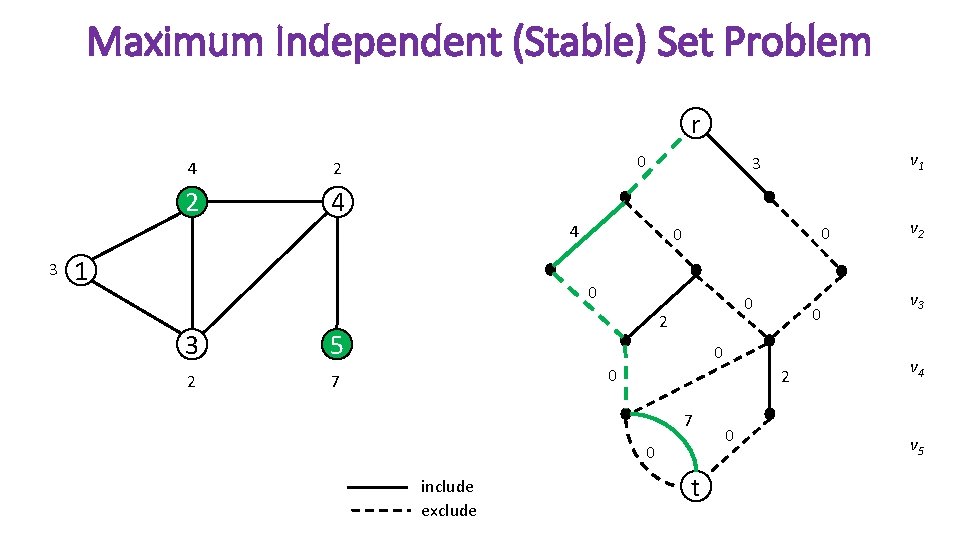
Maximum Independent (Stable) Set Problem r 4 2 2 4 0 4 3 1 0 0 0 3 5 2 7 v 1 3 0 2 0 0 0 2 7 0 include exclude t 0 v 2 v 3 v 4 v 5
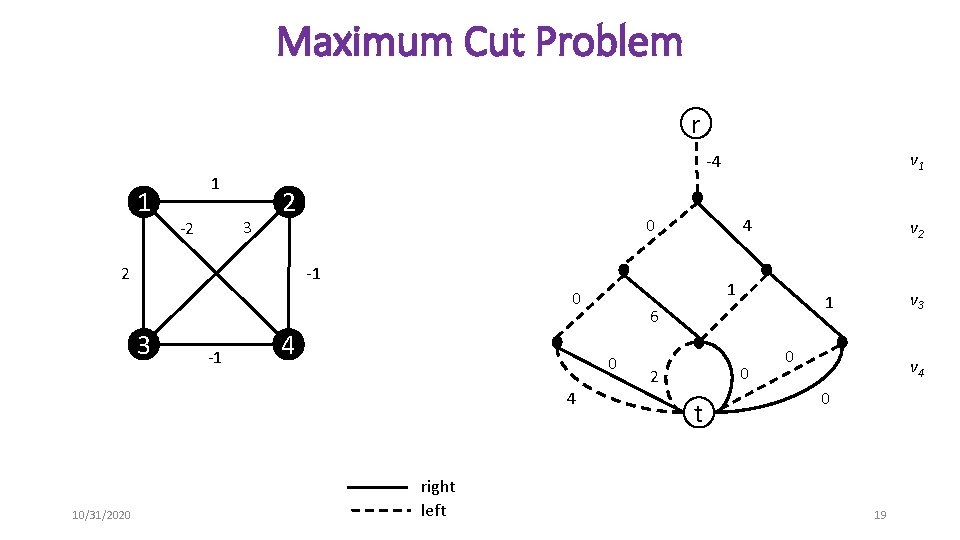
Maximum Cut Problem r 1 1 3 -2 2 2 0 -1 4 right left 0 2 t v 3 1 6 0 4 v 2 1 0 10/31/2020 4 -1 3 v 1 -4 0 v 4 0 19
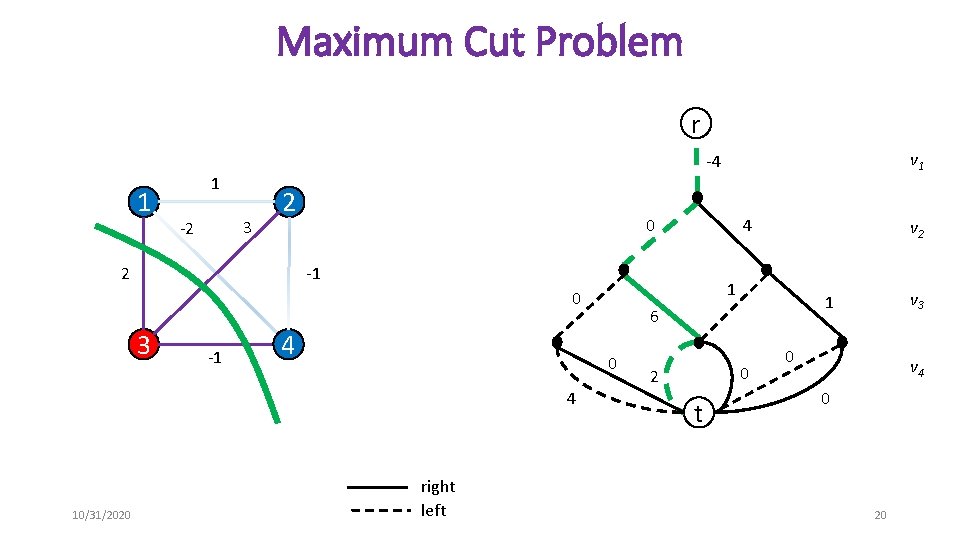
Maximum Cut Problem r 1 1 3 -2 2 2 0 -1 4 right left 0 2 t v 3 1 6 0 4 v 2 1 0 10/31/2020 4 -1 3 v 1 -4 0 v 4 0 20

Exact Decision Diagrams – Dynamic Programming • Exact decision diagram can be built several different ways • Incremental refinement • Top-down • Dynamic programming formulation • The decision diagram is the state transition graph 10/31/2020 23
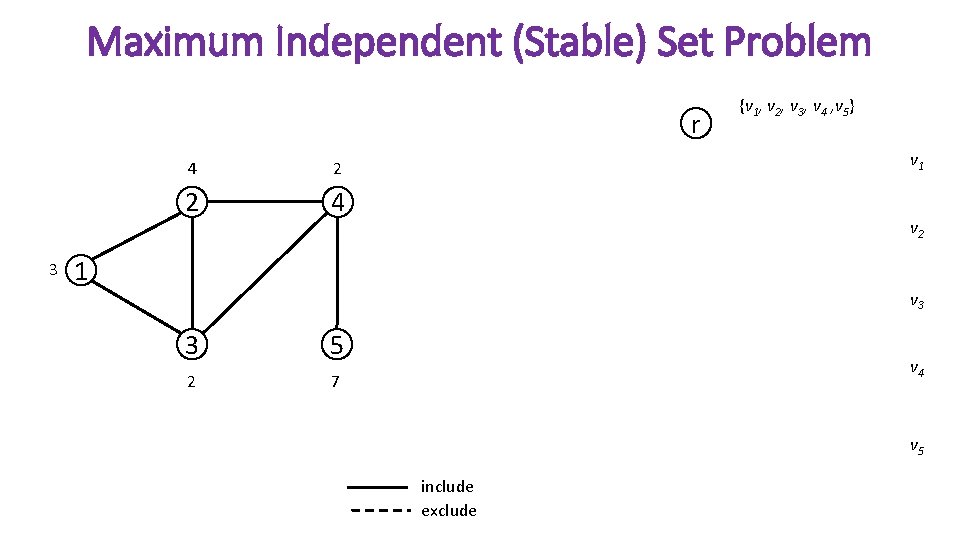
Maximum Independent (Stable) Set Problem r 3 4 2 2 4 {v 1, v 2, v 3, v 4 , v 5} v 1 v 2 1 v 3 3 5 2 7 v 4 v 5 include exclude
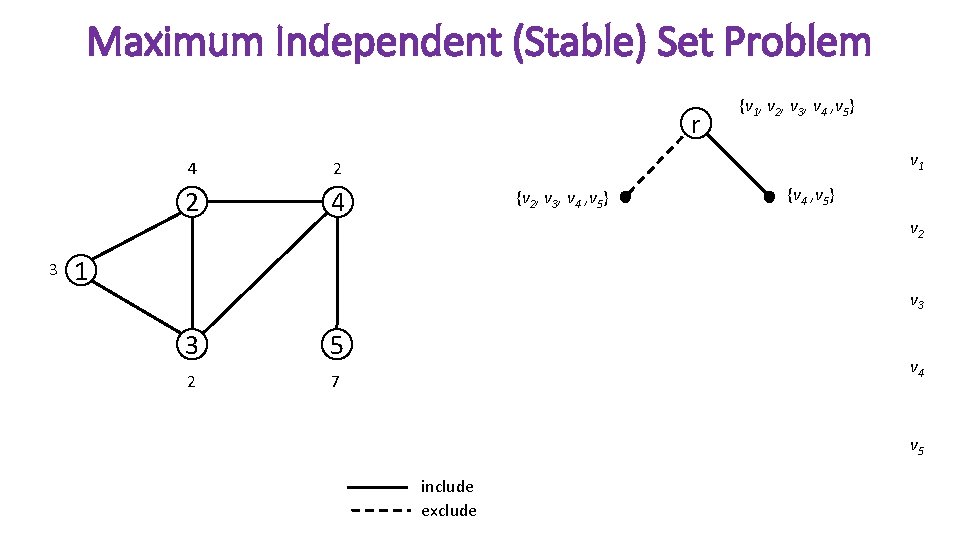
Maximum Independent (Stable) Set Problem r 3 4 2 2 4 {v 1, v 2, v 3, v 4 , v 5} v 1 {v 2, v 3, v 4 , v 5} {v 4 , v 5} v 2 1 v 3 3 5 2 7 v 4 v 5 include exclude
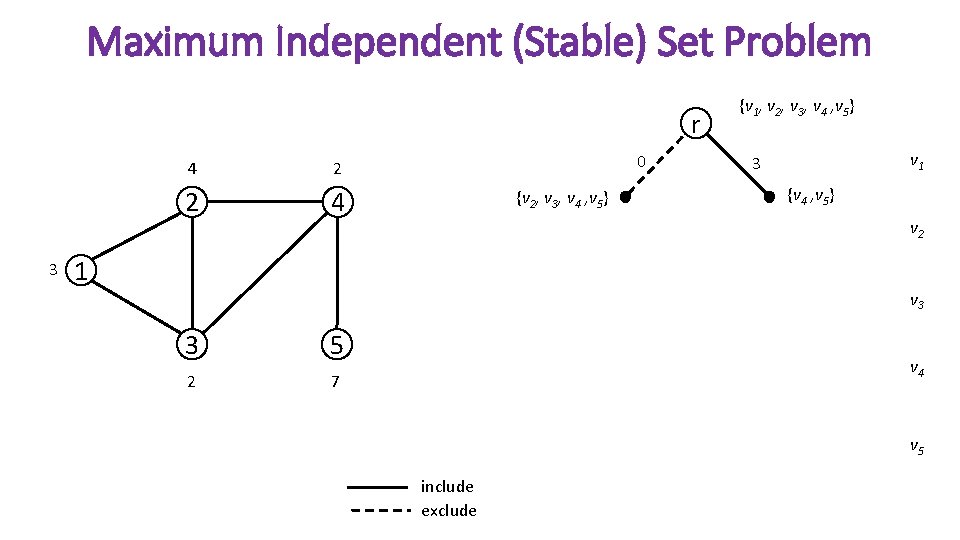
Maximum Independent (Stable) Set Problem r 3 4 2 2 4 0 {v 2, v 3, v 4 , v 5} {v 1, v 2, v 3, v 4 , v 5} v 1 3 {v 4 , v 5} v 2 1 v 3 3 5 2 7 v 4 v 5 include exclude
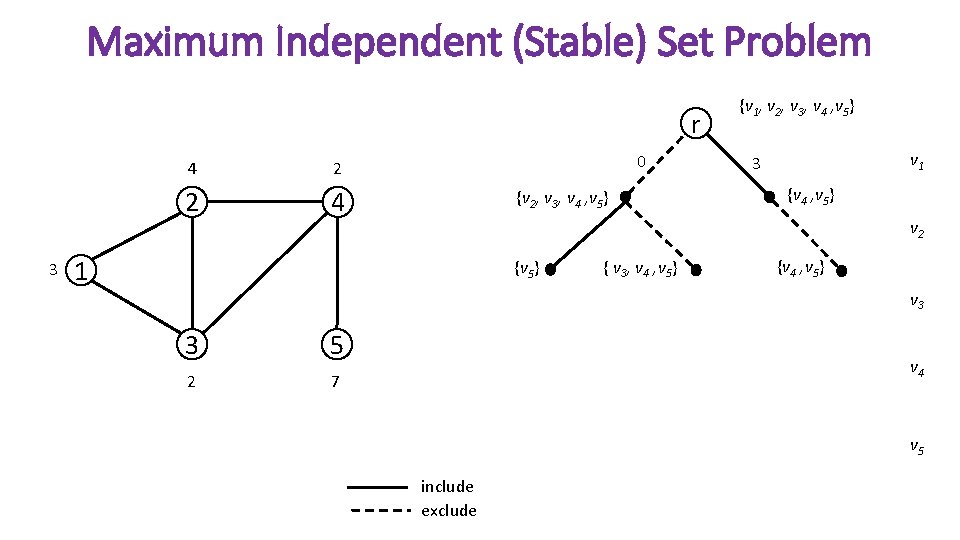
Maximum Independent (Stable) Set Problem r 3 4 2 2 4 0 {v 2, v 3, v 4 , v 5} {v 1, v 2, v 3, v 4 , v 5} v 1 3 {v 4 , v 5} v 2 1 {v 5} { v 3, v 4 , v 5} {v 4 , v 5} v 3 3 5 2 7 v 4 v 5 include exclude
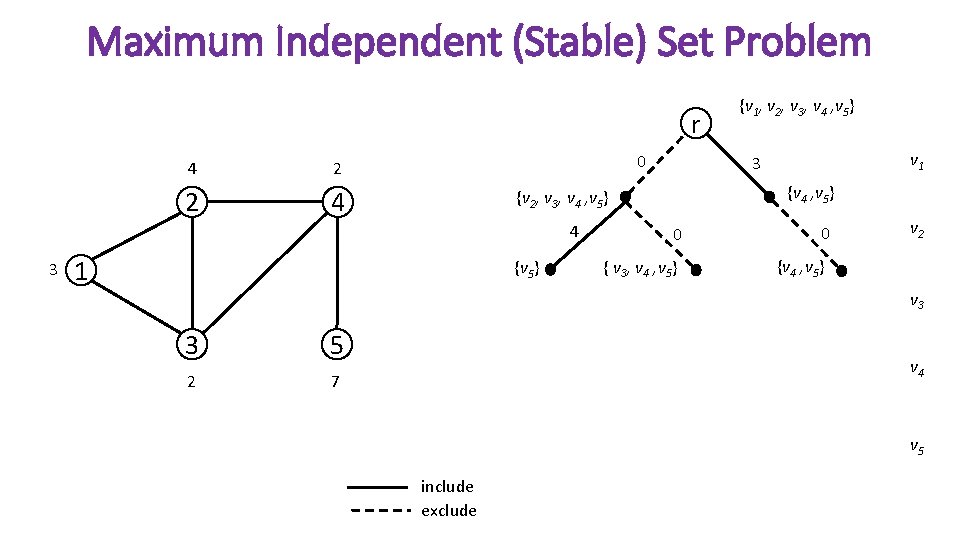
Maximum Independent (Stable) Set Problem r 4 2 2 4 0 3 1 {v 5} v 1 3 {v 4 , v 5} {v 2, v 3, v 4 , v 5} 4 {v 1, v 2, v 3, v 4 , v 5} 0 { v 3, v 4 , v 5} 0 v 2 {v 4 , v 5} v 3 3 5 2 7 v 4 v 5 include exclude
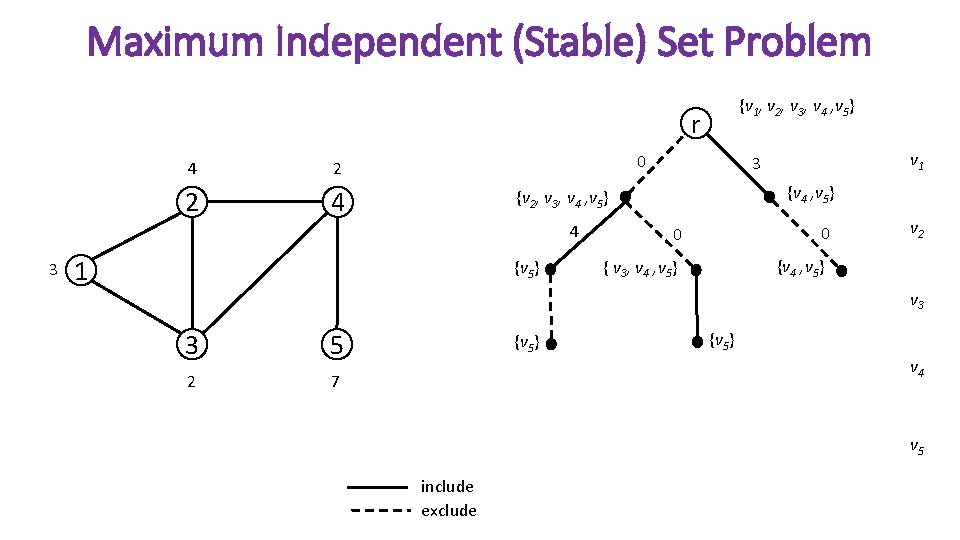
Maximum Independent (Stable) Set Problem {v 1, v 2, v 3, v 4 , v 5} r 4 2 2 4 0 3 {v 4 , v 5} {v 2, v 3, v 4 , v 5} 4 1 {v 5} v 1 3 0 0 v 2 {v 4 , v 5} { v 3, v 4 , v 5} v 3 3 5 2 7 {v 5} v 4 v 5 include exclude
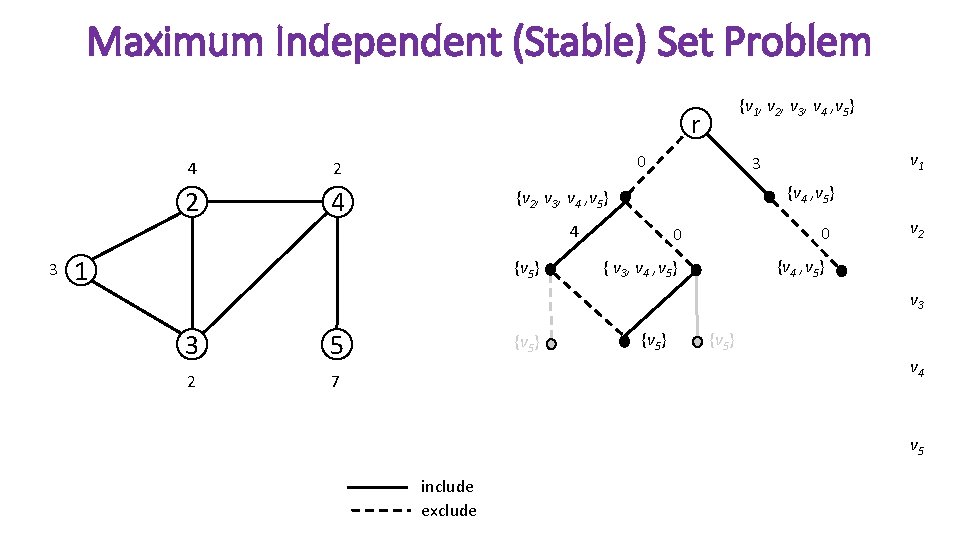
Maximum Independent (Stable) Set Problem {v 1, v 2, v 3, v 4 , v 5} r 4 2 2 4 0 {v 4 , v 5} {v 2, v 3, v 4 , v 5} 4 3 1 {v 5} v 1 3 0 0 v 2 {v 4 , v 5} { v 3, v 4 , v 5} v 3 3 5 2 7 {v 5} v 4 v 5 include exclude
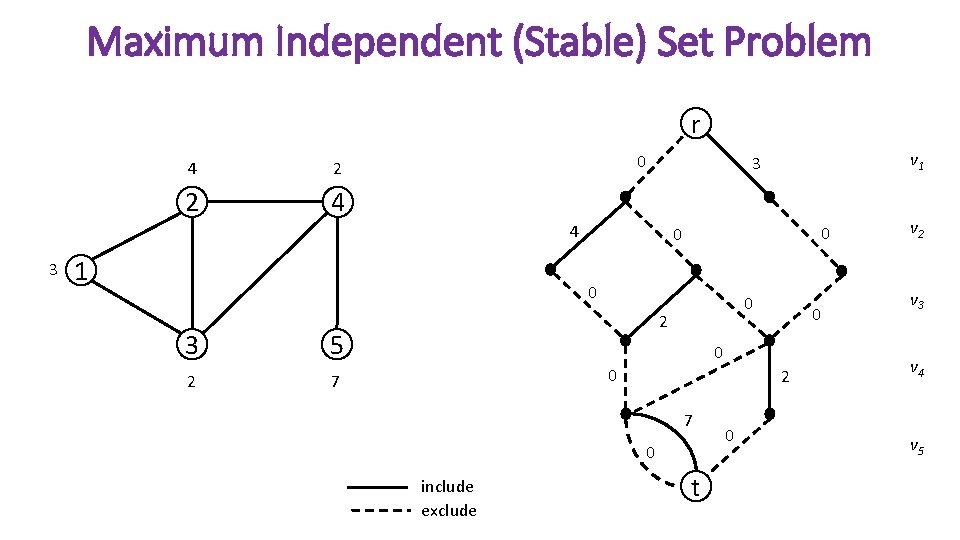
Maximum Independent (Stable) Set Problem r 4 2 2 4 0 4 3 1 0 0 0 3 5 2 7 v 1 3 0 2 0 0 0 2 7 0 include exclude t 0 v 2 v 3 v 4 v 5
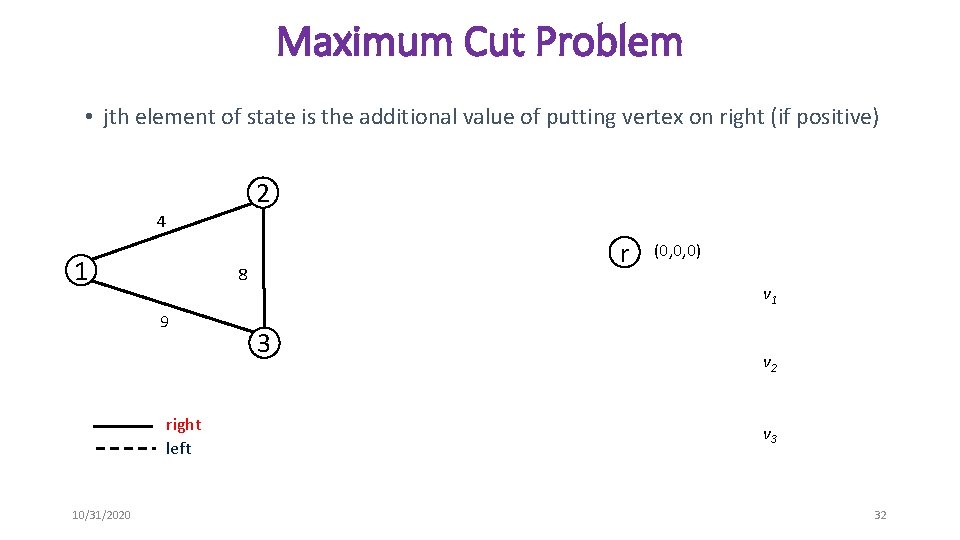
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 8 9 right left 10/31/2020 r (0, 0, 0) v 1 3 v 2 v 3 32
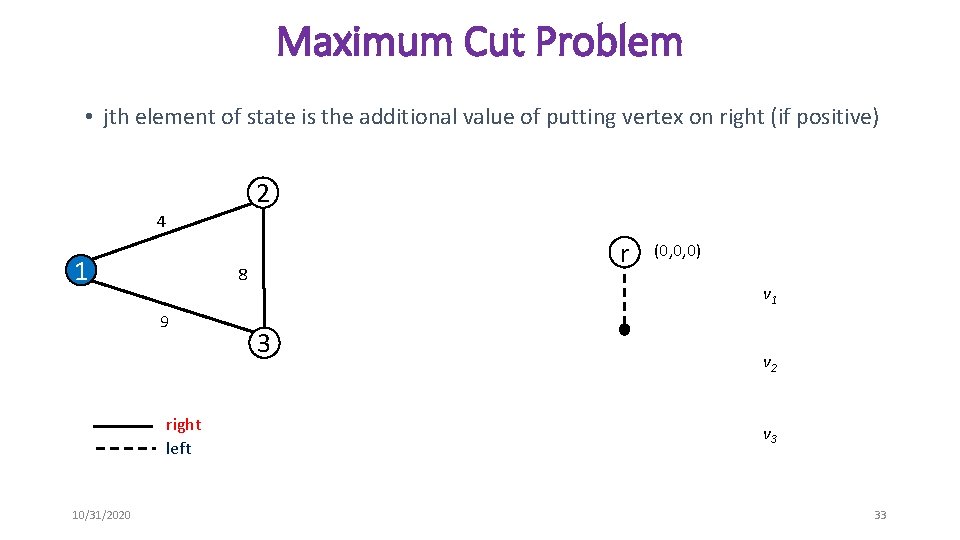
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 8 9 right left 10/31/2020 r (0, 0, 0) v 1 3 v 2 v 3 33
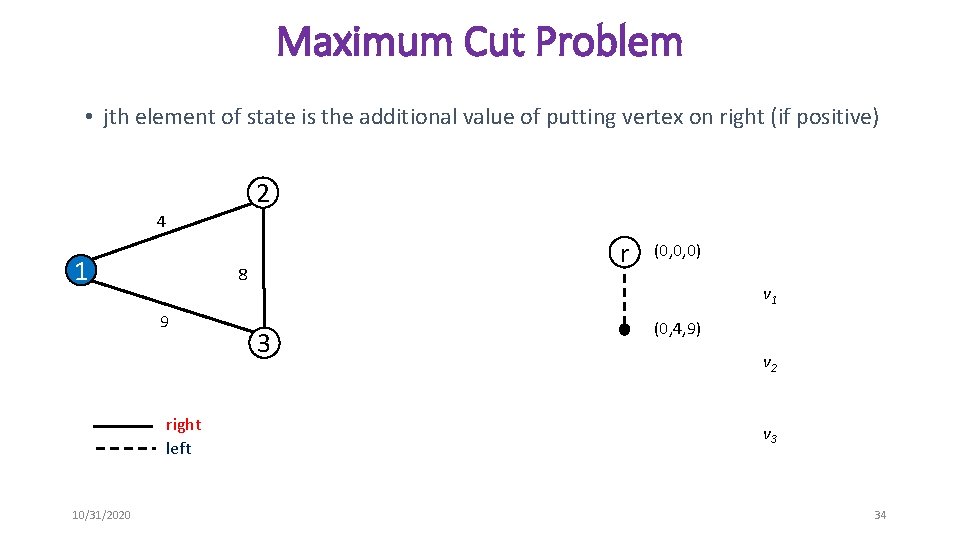
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 8 9 right left 10/31/2020 r (0, 0, 0) v 1 3 (0, 4, 9) v 2 v 3 34
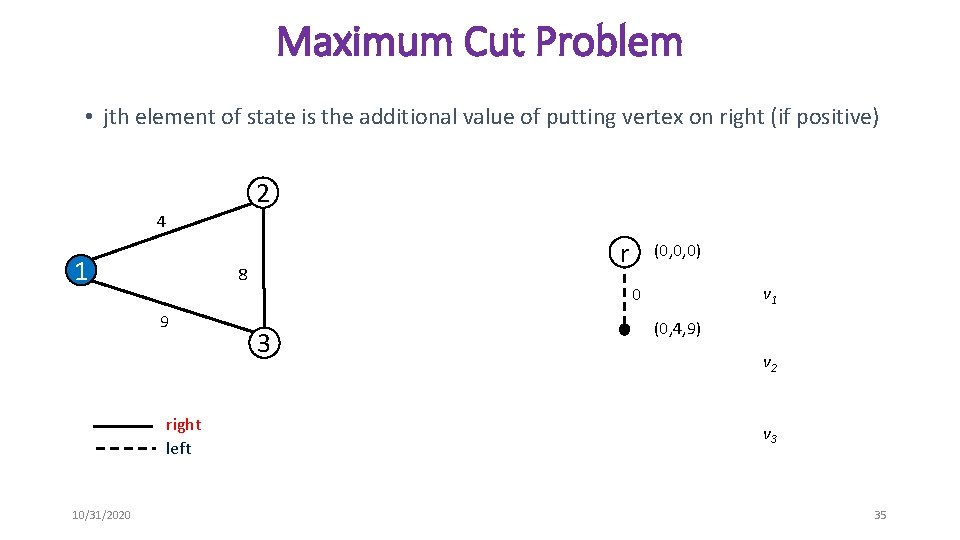
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 8 9 right left 10/31/2020 r (0, 0, 0) v 1 0 3 (0, 4, 9) v 2 v 3 35
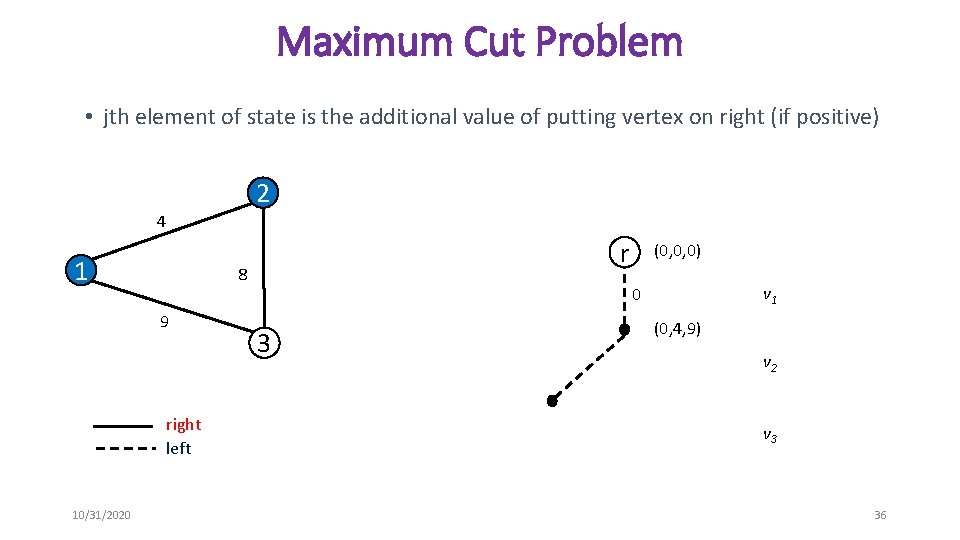
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 8 9 right left 10/31/2020 r (0, 0, 0) v 1 0 3 (0, 4, 9) v 2 v 3 36
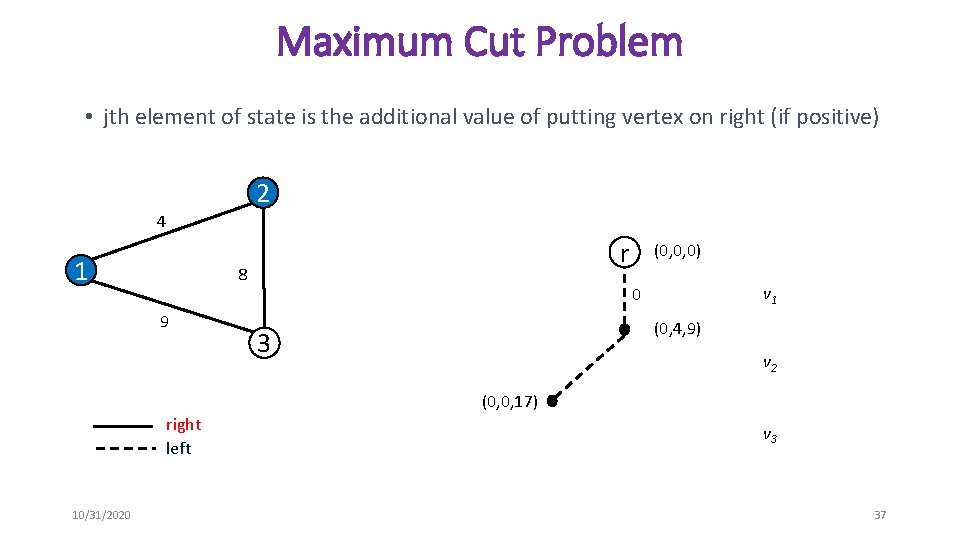
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 r 8 9 (0, 0, 0) v 1 0 (0, 4, 9) 3 v 2 (0, 0, 17) right left 10/31/2020 v 3 37
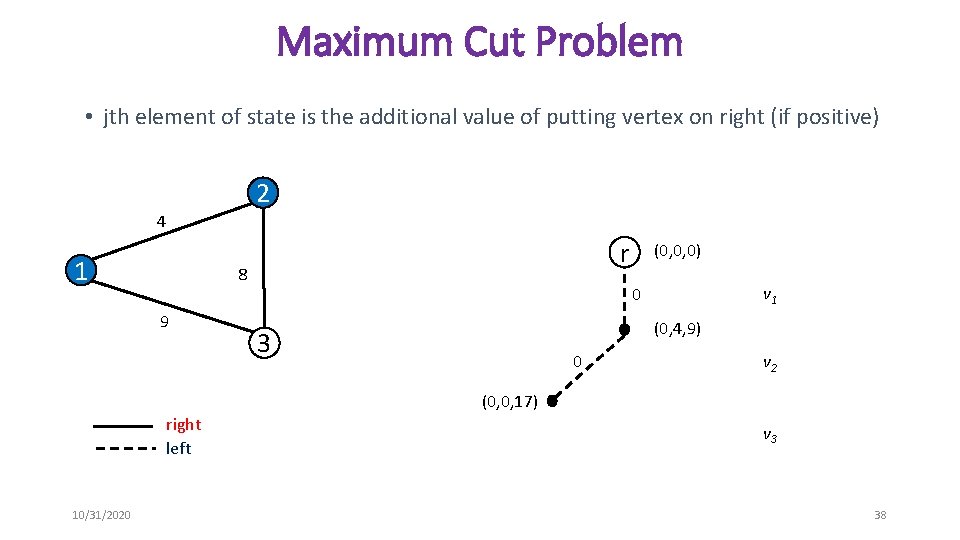
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 r 8 9 (0, 0, 0) v 1 0 (0, 4, 9) 3 0 v 2 (0, 0, 17) right left 10/31/2020 v 3 38
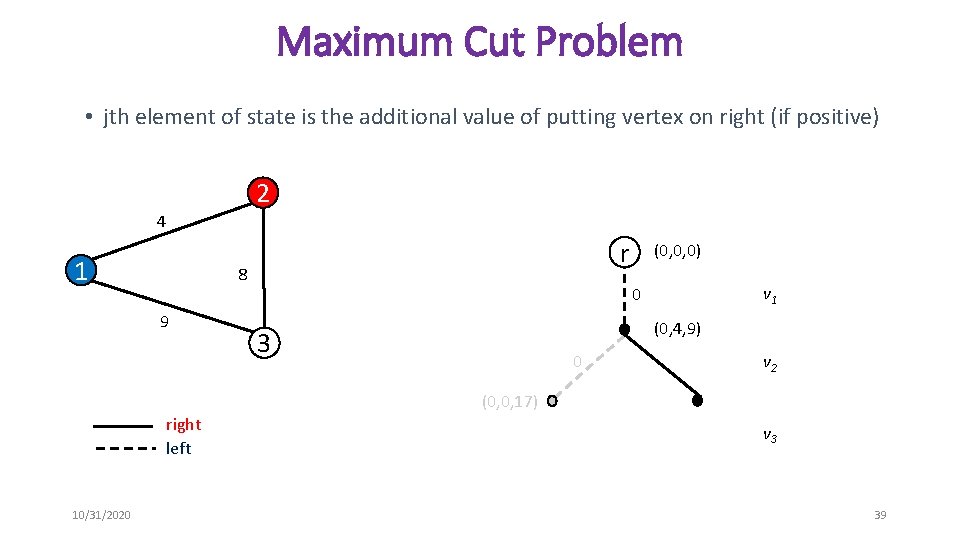
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 r 8 9 (0, 0, 0) v 1 0 (0, 4, 9) 3 0 v 2 (0, 0, 17) right left 10/31/2020 v 3 39
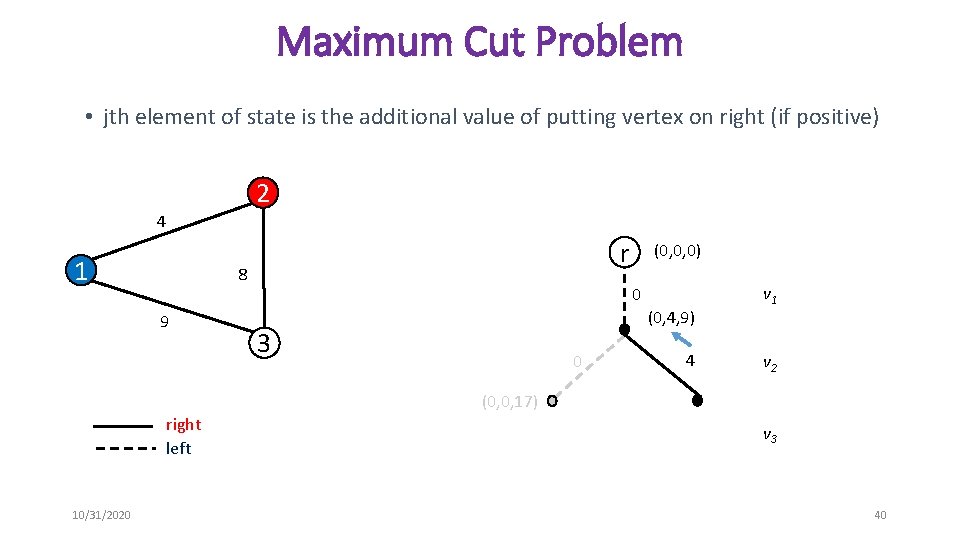
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 r 8 9 (0, 0, 0) 0 (0, 4, 9) 3 0 4 v 1 v 2 (0, 0, 17) right left 10/31/2020 v 3 40
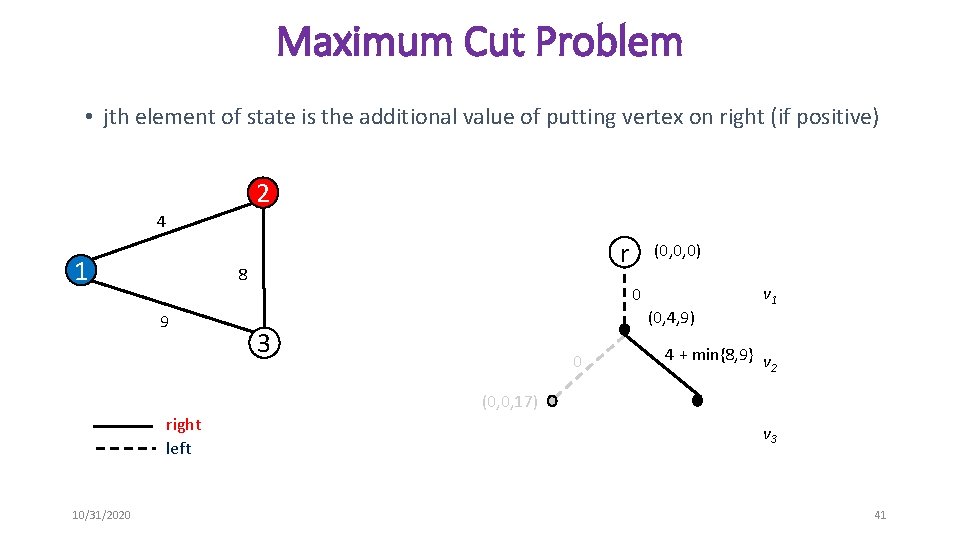
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 r 8 9 (0, 0, 0) 0 (0, 4, 9) 3 0 v 1 4 + min{8, 9} v 2 (0, 0, 17) right left 10/31/2020 v 3 41
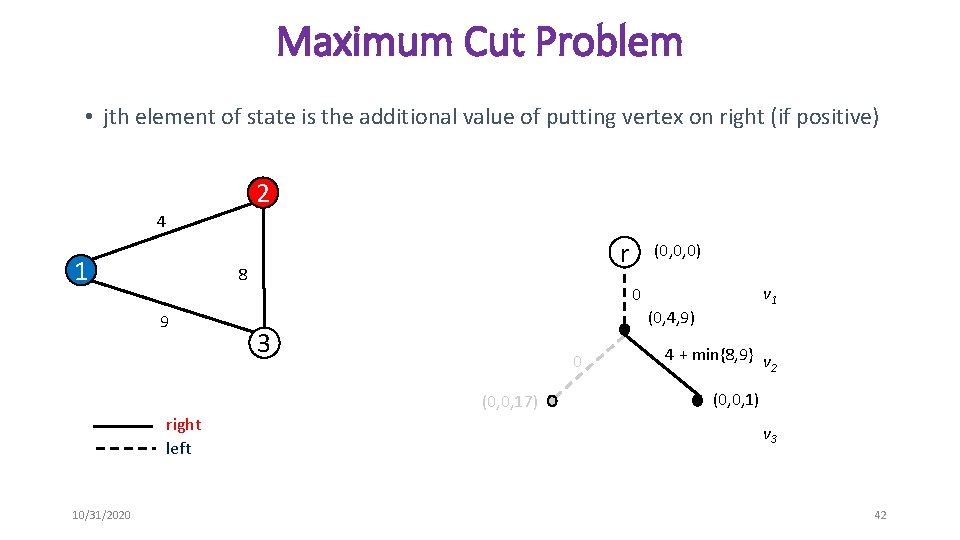
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 r 8 9 10/31/2020 v 1 0 (0, 4, 9) 3 0 (0, 0, 17) right left (0, 0, 0) 4 + min{8, 9} v 2 (0, 0, 1) v 3 42
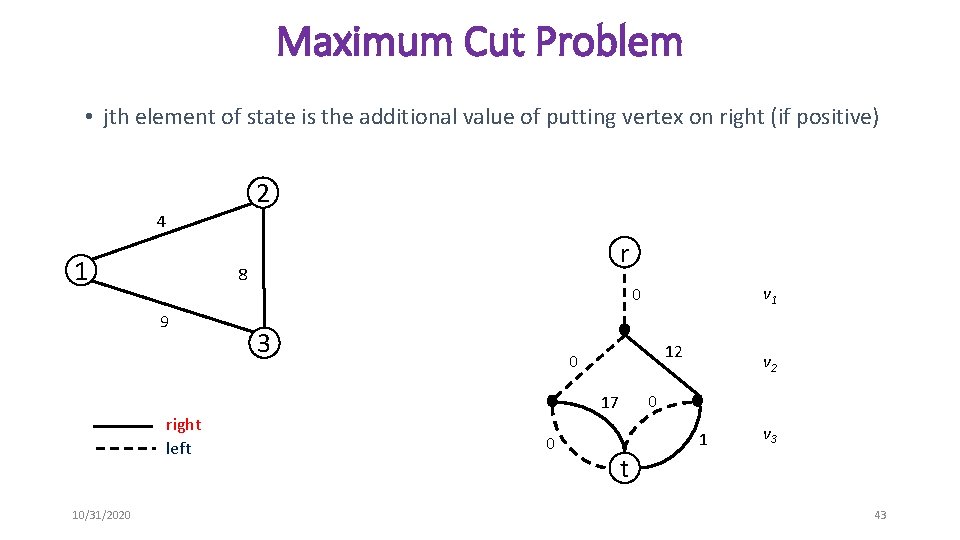
Maximum Cut Problem • jth element of state is the additional value of putting vertex on right (if positive) 2 4 1 r 8 9 3 12 0 10/31/2020 0 v 2 0 17 right left v 1 0 1 v 3 t 43

Outline • Applications • Exact decision diagrams • Approximate decision diagrams • The branch-and-bound algorithm • Computational results 10/31/2020 44

Approximate Decision Diagrams • In general, decision diagrams will grow exponentially large • They are a compact representation of the entire search space! • Limit the size to approximate the feasible space • Relaxed Decision Diagrams • Over-approximations of the feasible set • Length of each r-t path is greater than or equal to the objective value of the solution it represents • Restricted Decision Diagrams • Under-approximations of the feasible set • Length of each r-t path is less than or equal to the objective value of the solution it represents 10/31/2020 45
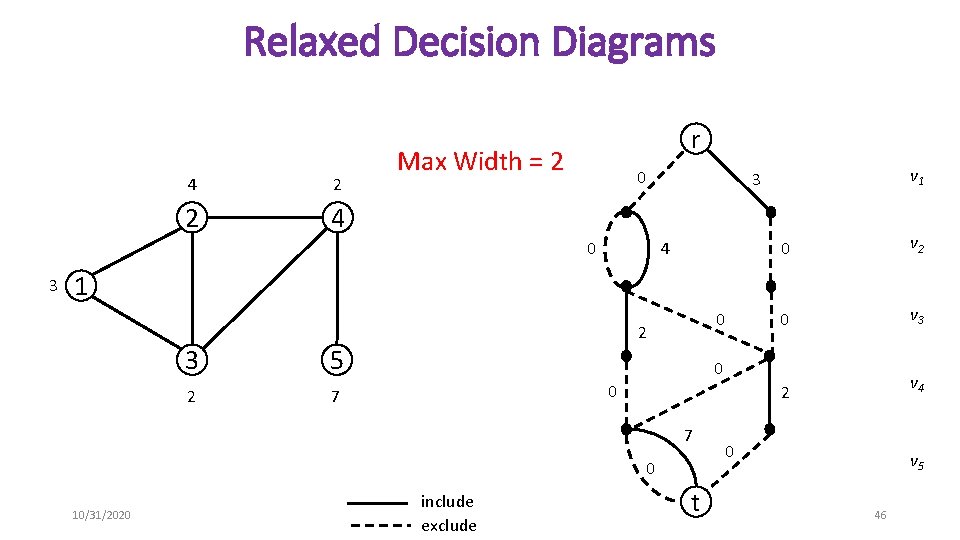
Relaxed Decision Diagrams 4 2 2 4 r Max Width = 2 0 0 3 v 1 3 4 0 v 2 0 v 3 2 v 4 1 3 2 0 2 5 0 0 7 7 0 10/31/2020 include exclude t 0 v 5 46
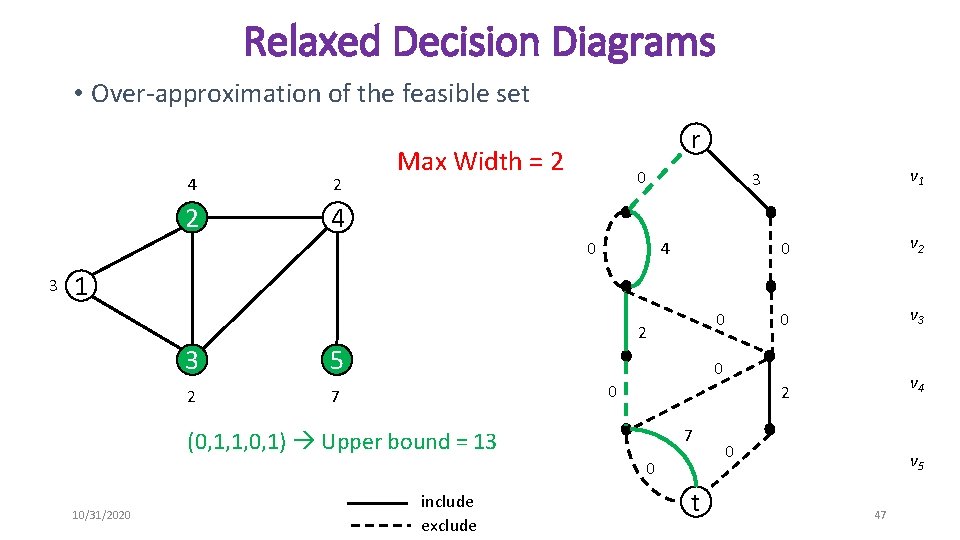
Relaxed Decision Diagrams • Over-approximation of the feasible set 4 2 2 4 r Max Width = 2 0 0 3 v 1 3 4 0 v 2 0 v 3 2 v 4 1 3 2 0 2 5 0 0 7 7 (0, 1, 1, 0, 1) Upper bound = 13 0 10/31/2020 include exclude t 0 v 5 47
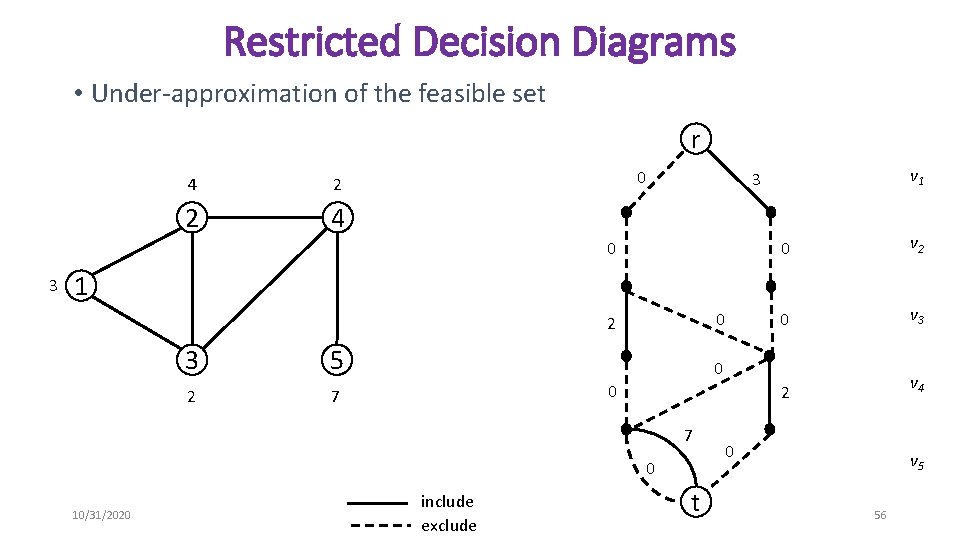
Restricted Decision Diagrams • Under-approximation of the feasible set r 4 2 2 4 0 0 3 v 1 3 0 v 2 0 v 3 2 v 4 1 0 2 3 2 5 0 0 7 7 0 10/31/2020 include exclude t 0 v 5 56
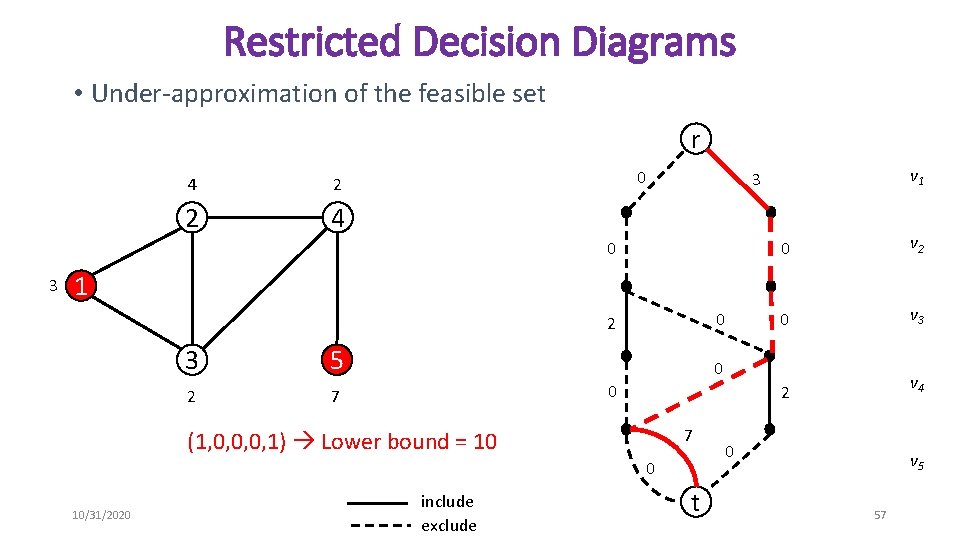
Restricted Decision Diagrams • Under-approximation of the feasible set r 4 2 2 4 0 0 3 v 1 3 0 v 2 0 v 3 2 v 4 1 0 2 3 2 5 0 0 7 7 (1, 0, 0, 0, 1) Lower bound = 10 0 10/31/2020 include exclude t 0 v 5 57

Outline • Applications • Exact decision diagrams • Approximate decision diagrams • The branch-and-bound algorithm • Computational results 10/31/2020 63
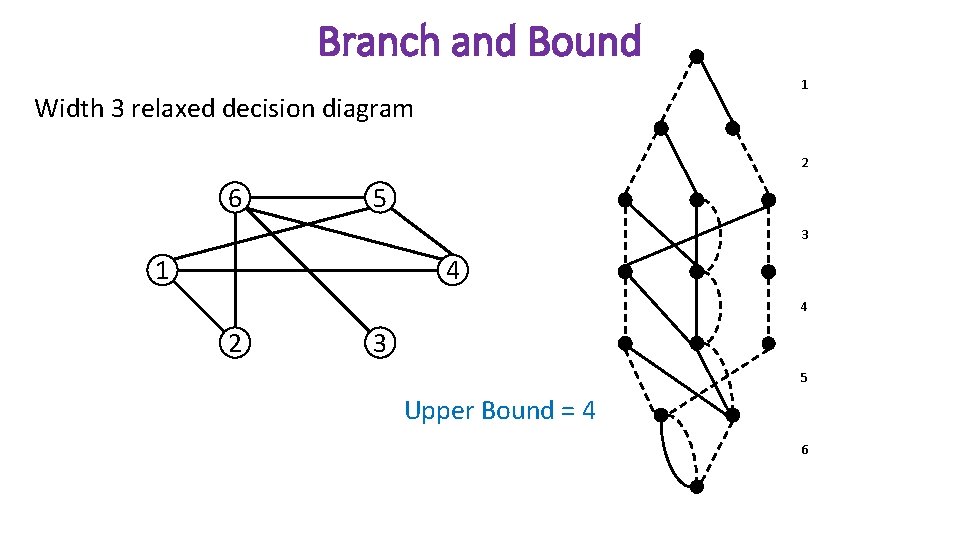
Branch and Bound 1 Width 3 relaxed decision diagram 2 6 5 3 1 4 4 2 3 5 Upper Bound = 4 6
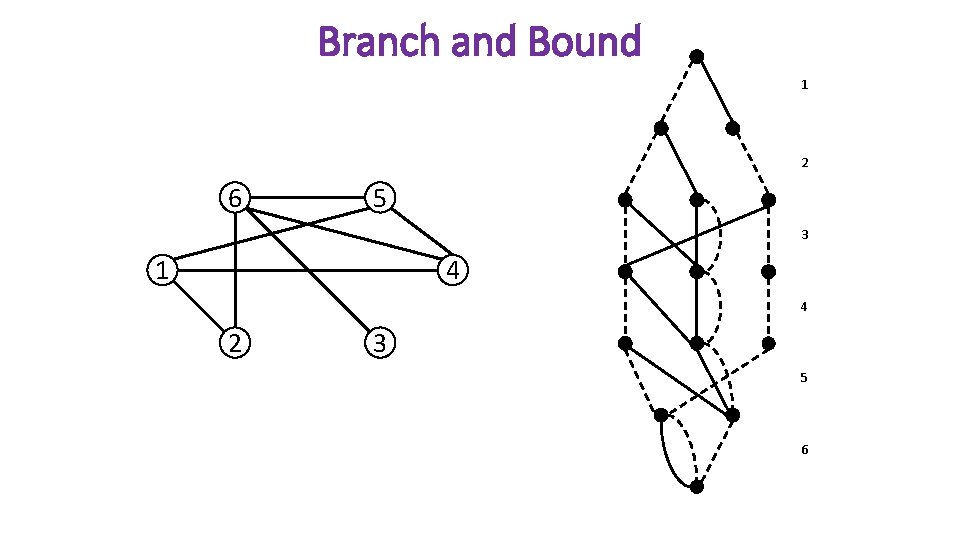
Branch and Bound 1 2 6 5 3 1 4 4 2 3 5 6
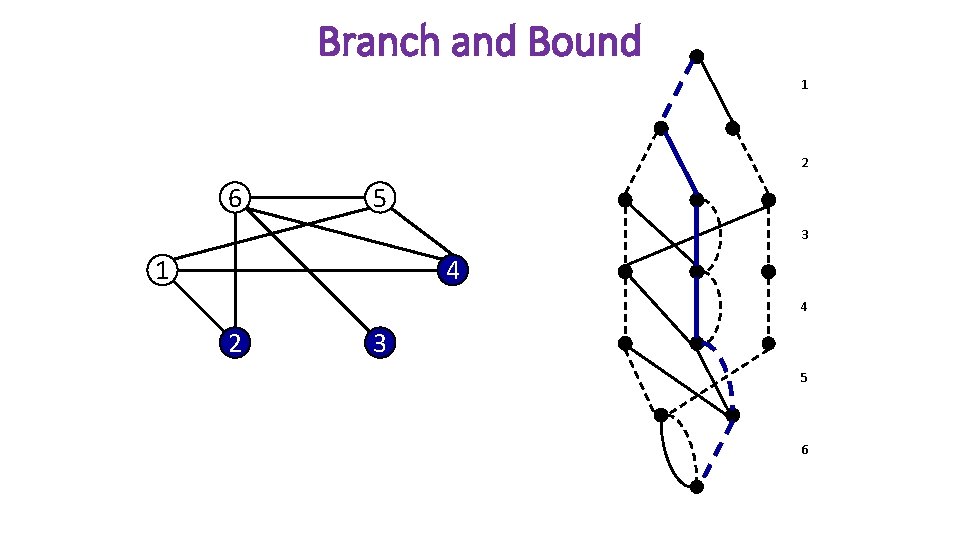
Branch and Bound 1 2 6 5 3 1 4 4 2 3 5 6
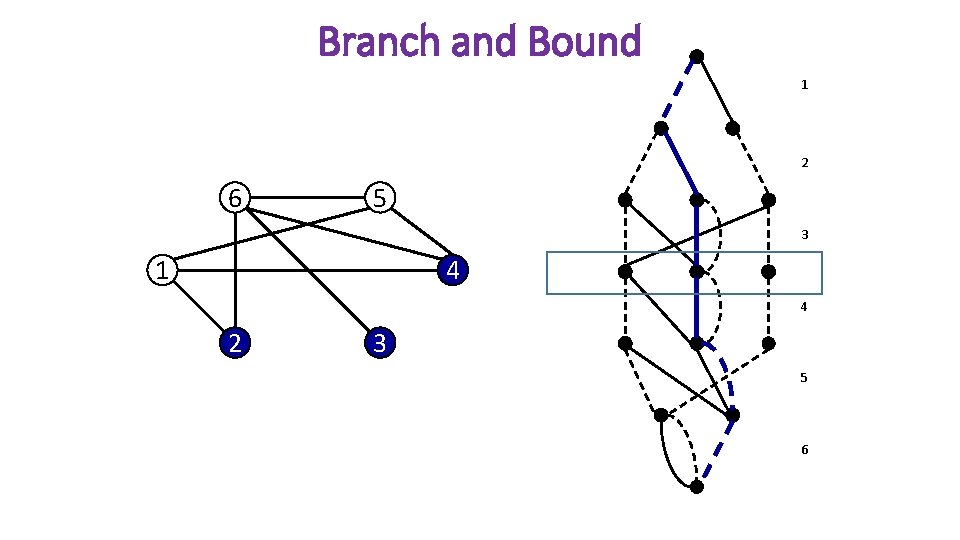
Branch and Bound 1 2 6 5 3 1 4 4 2 3 5 6
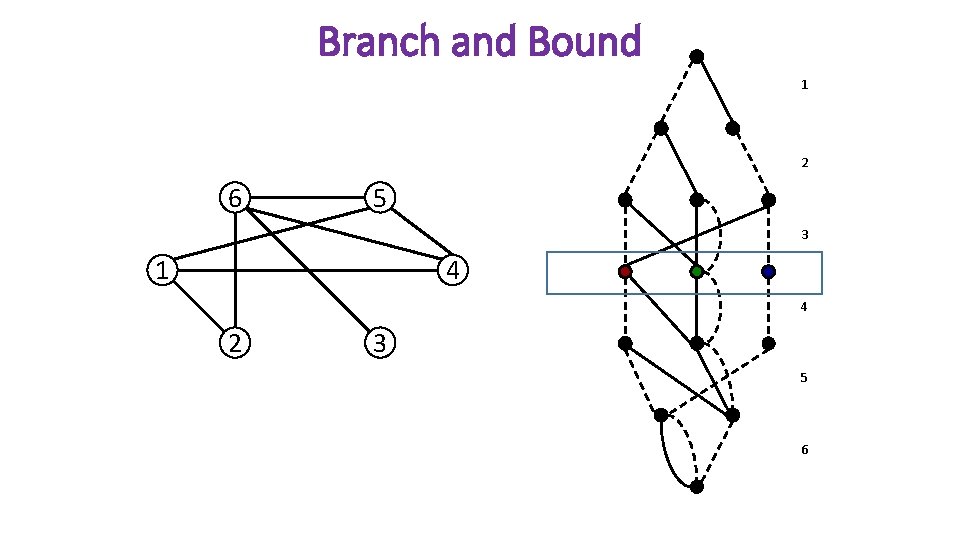
Branch and Bound 1 2 6 5 3 1 4 4 2 3 5 6

Branch and Bound 1 2 6 5 3 1 4 4 2 3 5 2 6

Branch and Bound 1 2 6 5 3 1 4 4 2 3 5 3 6
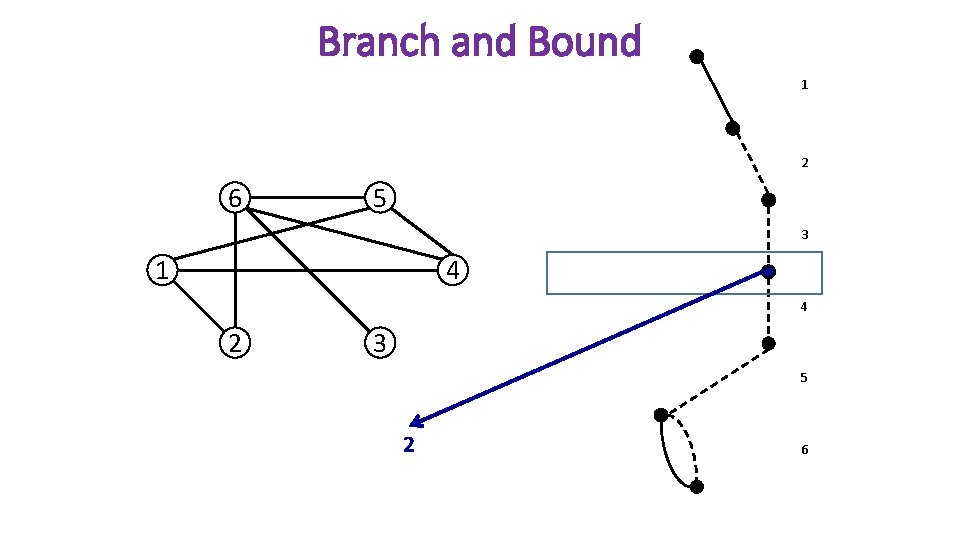
Branch and Bound 1 2 6 5 3 1 4 4 2 3 5 2 6
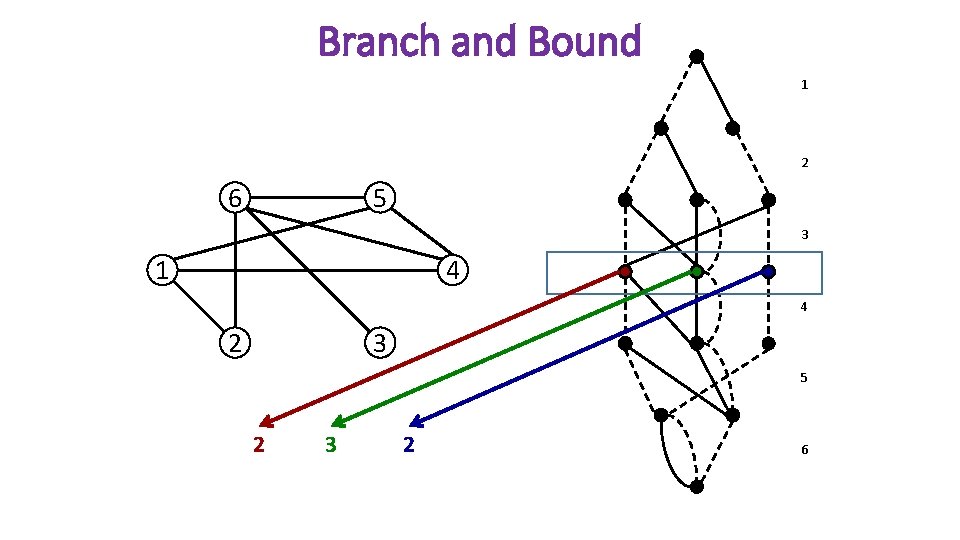
Branch and Bound 1 2 6 5 3 1 4 4 2 3 5 2 3 2 6
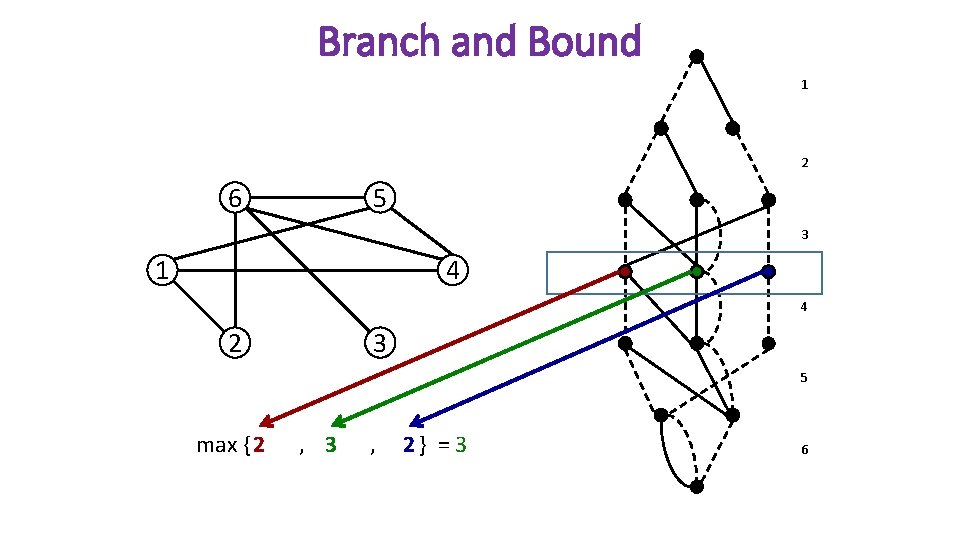
Branch and Bound 1 2 6 5 3 1 4 4 2 3 5 max { 2 , 3 , 2} = 3 6

New Branching Scheme • Novel branching scheme • Branch on pools of partial solutions • Remove symmetry from search • Symmetry with respect to feasible completions • Can be combined with other techniques • Use decision diagrams for branching, and LP for bounds

Outline • Applications • Exact decision diagrams • Approximate decision diagrams • The branch-and-bound algorithm • Computational results 10/31/2020 76

Computational Results • Compare with commercial solver CPLEX • State-of-the-art integer programming technology • Use typical, strong formulations • Independent set problem – edge formulation and clique formulation • O(n) variables, O(n 2) constraints • Maximum cut problem – triangle inequalities • O(n 2) variables, O(n 3) constraints 10/31/2020 77

Maximum Independent Set Problems • Randomly generated graphs • n = {250, 500, 750, 1000, 1250, 1500} • d = {. 1, . 2, …, . 9} • Unit objective function • Benchmark problems • DIMACS • Compare end gaps after 1800 seconds 10/31/2020 78
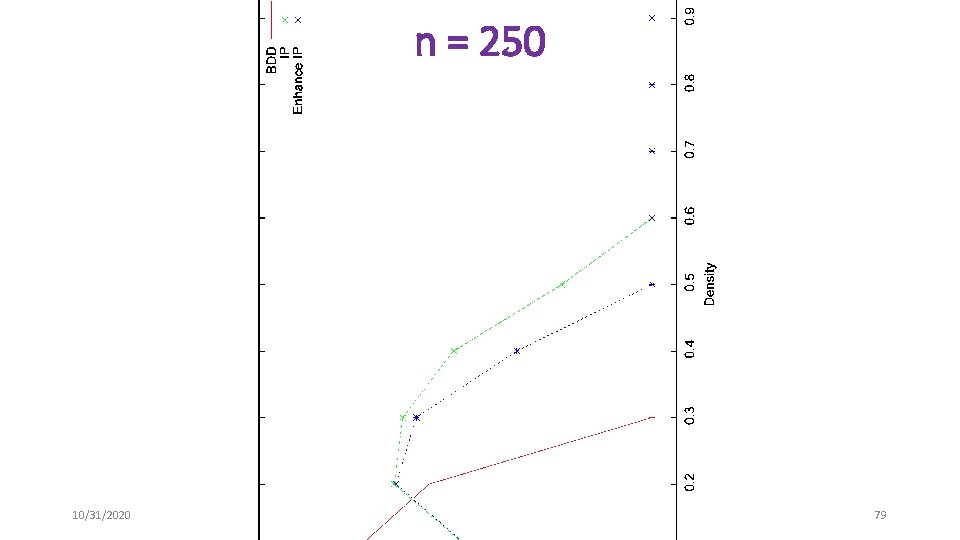
n = 250 10/31/2020 79
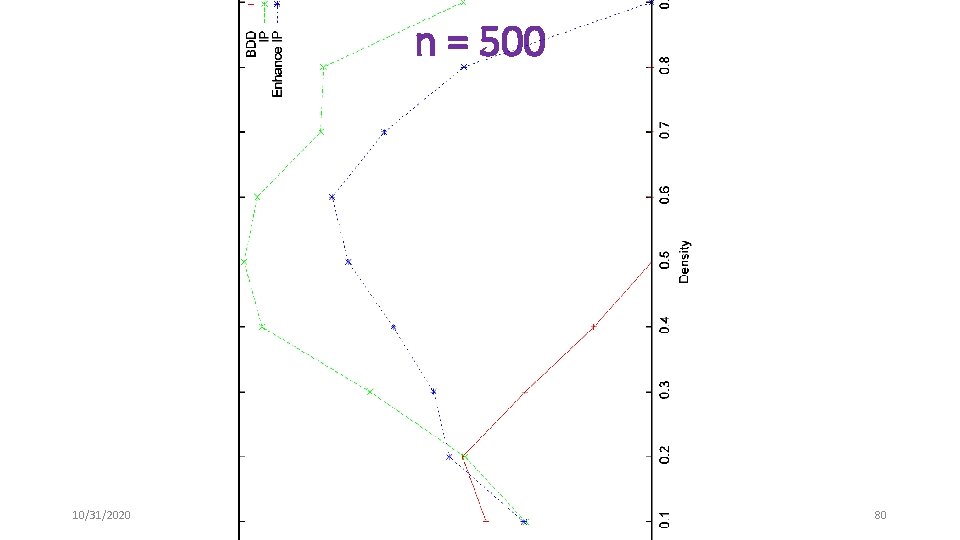
n = 500 10/31/2020 80
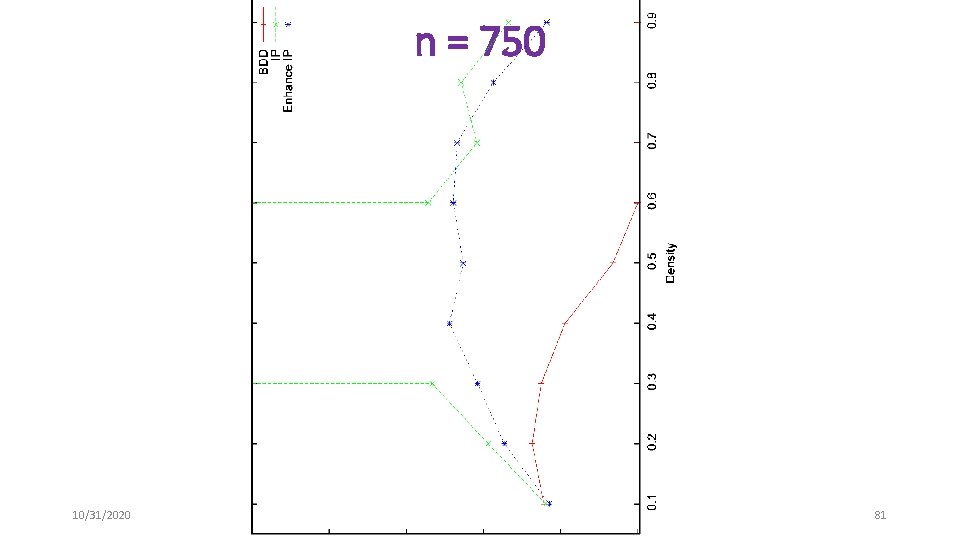
n = 750 10/31/2020 81
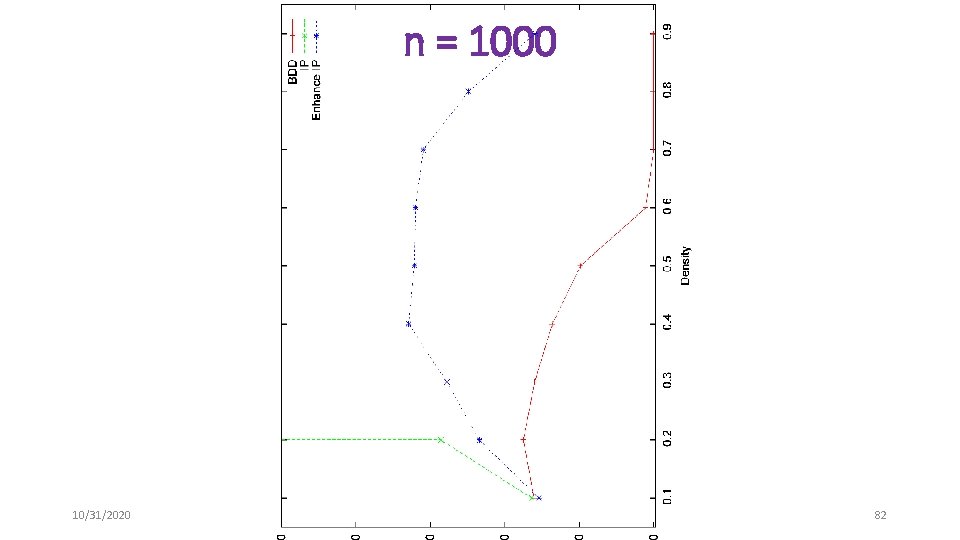
n = 1000 10/31/2020 82
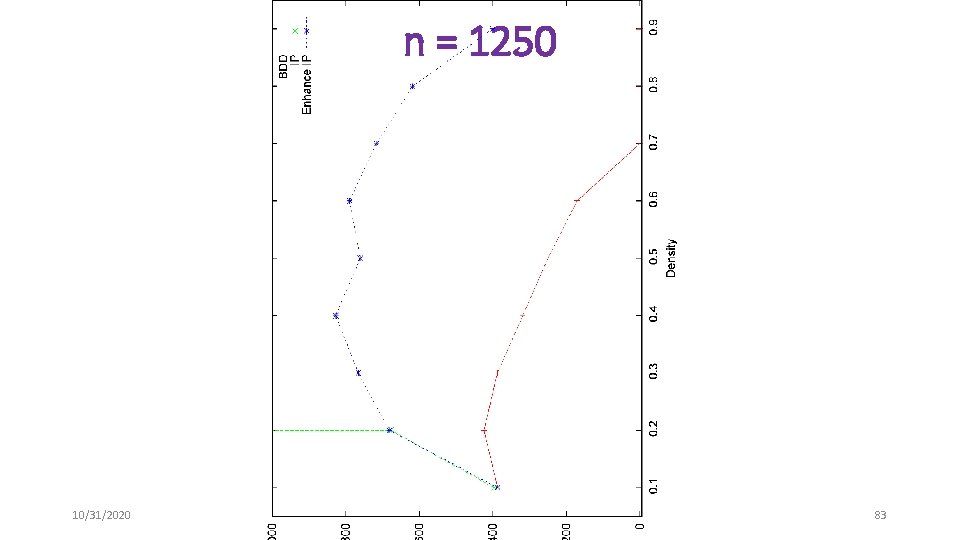
n = 1250 10/31/2020 83
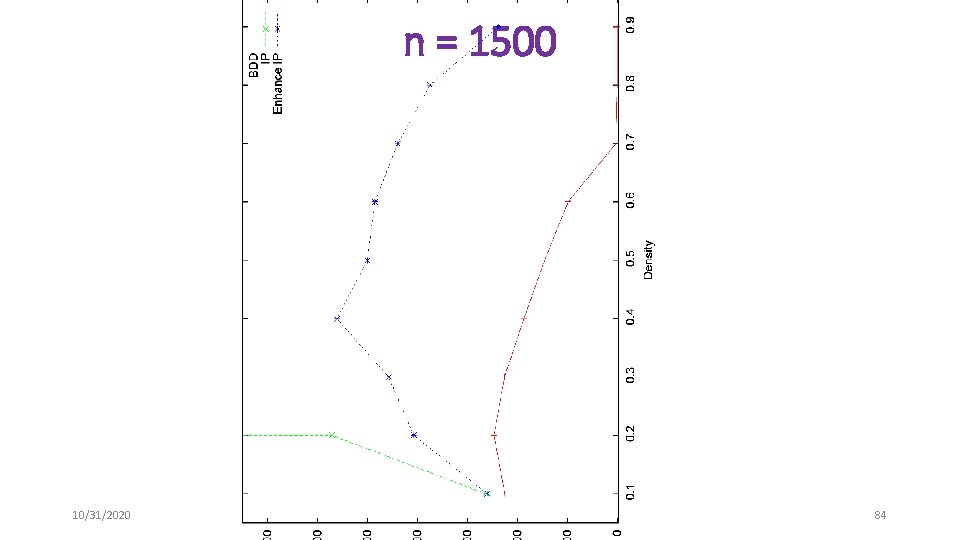
n = 1500 10/31/2020 84
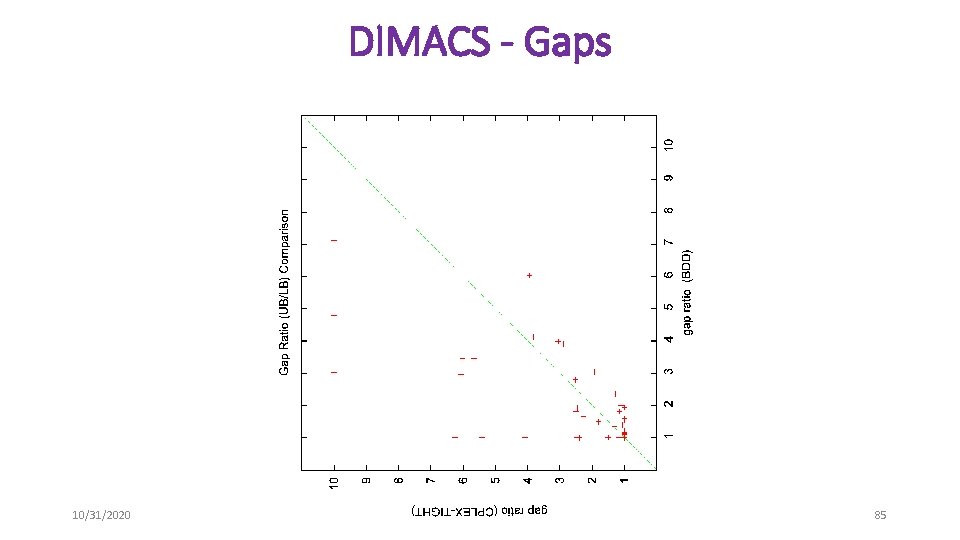
DIMACS - Gaps 10/31/2020 85

Maximum Cut Problems • Benchmark problems • g instances • Helmberg and Rendl instances, which were taken from Rinaldi’s random graph generator • n ranges from 800 to 3000 – very large/difficult problems, mostly open • Compared performance with Biq. Mac 10/31/2020 86
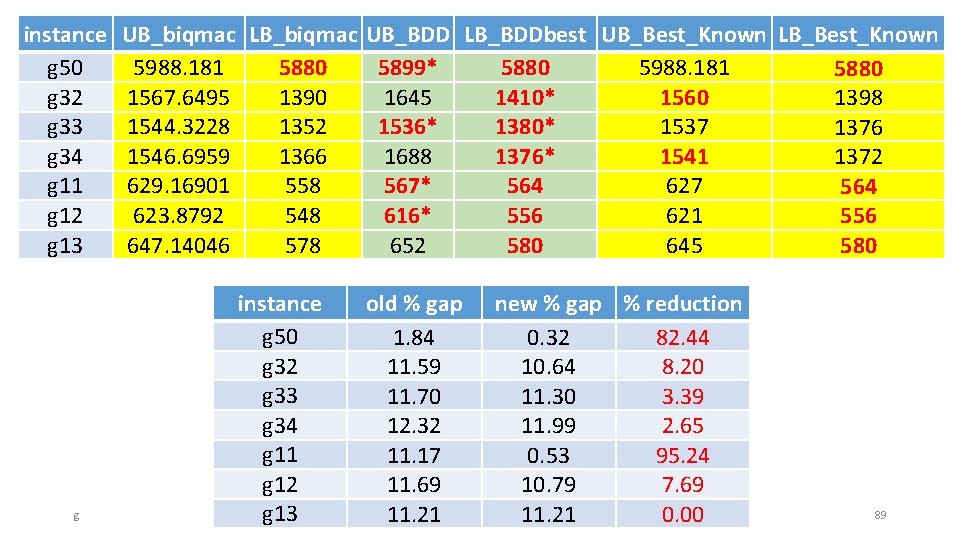
instance g 50 g 32 g 33 g 34 g 11 g 12 g 13 g UB_biqmac LB_biqmac UB_BDD LB_BDDbest UB_Best_Known LB_Best_Known 5988. 181 5880 5899* 5880 5988. 181 5880 1567. 6495 1390 1645 1410* 1560 1398 1544. 3228 1352 1536* 1380* 1537 1376 1546. 6959 1366 1688 1376* 1541 1372 629. 16901 558 567* 564 627 564 623. 8792 548 616* 556 621 556 647. 14046 578 652 580 645 580 instance g 50 g 32 g 33 g 34 g 11 g 12 g 13 old % gap 1. 84 11. 59 11. 70 12. 32 11. 17 11. 69 11. 21 new % gap % reduction 0. 32 82. 44 10. 64 8. 20 11. 30 3. 39 11. 99 2. 65 0. 53 95. 24 10. 79 7. 69 11. 21 0. 00 89

Conclusion • New technique for discrete optimization • Decision diagrams replace LP relaxations • Relaxation bounds, primal heuristic, branching • The algorithm has be applied in the context of several discrete optimization problems • Set covering, set packing, independent set, maximum cut, maximum 2 satisfiability, … • The list is growing • In many cases, the algorithm outperforms state-of-the-art integer programming technology • Also has determined better solutions than have ever been identified 10/31/2020 90

THANK YOU! 10/31/2020 91
- Slides: 70