Decision Analysis Lecture 10 Tony Cox My email

Decision Analysis Lecture 10 Tony Cox My e-mail: tcoxdenver@aol. com Course web site: http: //cox-associates. com/DA/

Agenda • • • Problem set 8 solutions; Problem set 9 Hypothesis testing: statistical decision theory view Updating normal distributions Quality control: Sequential hypothesis testing Adaptive decision-making – – Exploration vs. exploitation Upper confidence band (UCB) algorithm Thompson sampling for adaptive Bayesian control Optimal stopping problems • Influence diagrams and Bayesian networks 2

Recommended Readings • Optimal learning. Powell and Frazier, 2008, pp 213, 216 -219, 223 -4, https: //pdfs. semanticscholar. org/42 d 8/34 f 981772 af 218022 be 071 e 739 fd 96882 b 12. pdf • How can decision-making be improved? Milkman et al. , 2008 http: //www. hbs. edu/faculty/Publication%20 Files/08 -102. pdf • Simulation-optimization tutorial (Carson & Maria, 1997) (Just skim this one) https: //pdfs. semanticscholar. org/e 5 d 8/39642 da 3565864 ee 9 c 043 a 726 ff 538477 dca. pdf • Causal graphs (Elwert, 2013), pp. 245 -250 https: //www. wzb. eu/sites/default/files/u 31/elwert_2013. pdf 3

Homework #8 (Due by 4: 00 PM, April 4) 1. An investment yields a normally distributed return with mean $2000 and standard deviation $1500. Find (a) Pr(loss) and (b) Pr(return > $4000). 2. If there are on average 3. 6 chocolate chips per cookie, what is the probability of finding (a) No chocolate chips; (b) Fewer than 5 chocolate chips; or (c) more than 10 chocolate chips in a randomly selected cookie? 3. A strike lasts for a random amount of time, T, having an exponential distribution with a mean of 10 days. What is the probability that the strike lasts (a) Less than 1 day; (b) Less than 6 days; (c) Between 6 and 7 days; (d) Less than 7 days if it has lasted six days so far? 4. How would the answers to problem 3 change if T were uniformly distributed between 0 and 20. 5 days? 5. A production process for glass bottles creates an average of 1. 1 bubbles per bottle. Bottles with more than 2 bubbles are classified as non-conforming and sent to recycling. Bubbles occur independently of each other. What is the probability that a randomly chosen bottle is non-conforming? 4

Solution to HW 8 problem 1 (Investment) • Normal: If return has mean $2000 and standard deviation $1500, find P(loss) and P(return > $4000)? a. pnorm(0, 2000, 1500) = pnorm(-2000/1500, 0, 1) = 0. 09121122; b. 1 - pnorm(4000, 2000, 1500) = 1 - pnorm(2000/1500, 0, 1) = 0. 09121122 5

Solution to HW 8 problem 2 (chocolate chips) • If there are on average 3. 6 chocolate chips per cookie, what is the probability of finding (a) No chocolate chips; (b) < 5 chocolate chips; or (c) > 10 chocolate chips in a randomly selected cookie? a. dpois(0, 3. 6)) = 0. 02732372 b. ppois(4, 3. 6) = 0. 7064384 c. 1 -ppois(10, 3. 6) = 0. 001271295 6

Solutions to HW 8 problem 5 (bubbles) • P(more than 2 bubbles | r = 1. 1 bubbles per bottle) = 1 - ppois(2, 1. 1) = 0. 09958372 ≈ 0. 1 7

Solutions to HW 8 problem 3 (exponential strike) a. P(strike lasts < 1 day) = pexp(1, 0. 1) = 1 exp(-m*t) = 1 - exp(-0. 1*1) = 0. 09516258 – pexp(t, r) = P(T < t | r arrivals per unit time) = P(T < t | 1/r mean time to arrival) b. P(strike < 6 days) = pexp(6, 0. 1) =1 - exp(-0. 1*6) = 0. 451188 c. P(6 < T < 7) = pexp(7, 0. 1) - pexp(6, 0. 1) = 1 - exp(-7*0. 1) – [1 – exp(-6*0. 1)] = exp(-6*0. 1) - exp(-7*0. 1) = 0. 05222633 8

Solutions to HW 8 problem 3 (exponential strike) d. P(T < 7 | T > 6) = P(6 < T < 7)/P(T > 6) (by definition of conditional probability, P(A | B) = P(A & B)/P(B), A = 6 < T, B = T < 7) = (pexp(7, 0. 1)-pexp(6, 0. 1))/(1 -pexp(6, 0. 1)) = 0. 09516258 (memoryless, so same as for part a) 9

Solutions to HW 8 problem 4 (uniform strike) a. P(T < 1) = 1/10. 5 = punif(1, 0, 10. 5) = 0. 0952381 b. P(T < 6) = 6/10. 5 = punif(6, 0, 10. 5) = 0. 5714286 c. P(6 < T < 7) = (7 – 6)/10. 5 = punif(7, 0, 10. 5) - punif(6, 0, 10. 5)= 0. 0952381 d. P(T < 7 | T > 6) = P(6 < T < 7)/P(T > 6) = 0. 0952381 /(1 - 0. 5714286) = 0. 22222 e. Not memoryless: 0. 22 > 0. 0952 10

Homework #9, Problem 1 (Due by 4: 00 PM, April 11) • Starting from a uniform prior, U[0, 1], for success probability, you observe 22 successes in 30 trials. • What is your Bayesian posterior probability that the success probability is greater than 0. 5? 11

Homework #9, Problem 2 (Due by 4: 00 PM, April 11) • In a manufacturing plant, it costs $10/day to stock 1 spare part, $20/day to stock 2 spare parts, etc. ($10 per spare part per day). • There are 50 machines in the plant. Each machine breaks with probability 0. 004 per machine per day. (More than one machine can fail on the same day. ) • If a spare part is available (in stock) when a machine breaks, it can be repaired immediately, and no production is lost. • If no spare part is available when a machine breaks, it is idle until a new part can be delivered (1 day lag). $65 of production is lost. • How many spare parts should the plant manager keep in stock to minimize expected loss? 12

Homework #9 discussion problem for April 11 (uncollected/ungraded) • • Choice set: Take or Do Not Take Chance set (states): Sunshine or Rain P(Sunshine) = p = 0. 6 Utilities of act-state pairs: – u(Take, Sunshine) = 80 – u(Take, Rain) = 80 – u(Do Not Take, Sunshine) = 100 – u(Do Not Take, Rain) = 0 13

Homework #9 discussion problem (uncollected/ungraded) 1. If p = 0. 6, find EU(Take) and EU(Don’t Take) using Netica – Goal is to see how Netica deals with decisions and expected utilities – May also try it via simulation 2. Update these EUs if a forecast (with error probability 0. 2) predicts rain 14

Hypothesis testing (Cont. ) 15

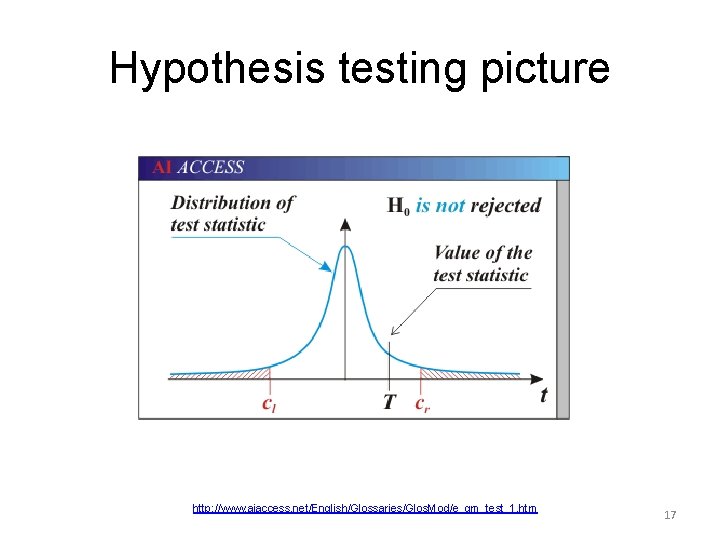
Logic and vocabulary of statistical hypothesis testing • Formulate a null hypothesis to be tested, H 0 – H 0 is “What you are trying to reject” – If true, H 0 determines a probability distribution for the test statistic (a function of the data) • Choose = significance level for test = P(reject null hypothesis H 0 | H 0 is true) • Decision rule: Reject H 0 if and only if the test statistic falls in a critical region of values that are unlikely (p < ) if H 0 is true. 16

Hypothesis testing picture http: //www. aiaccess. net/English/Glossaries/Glos. Mod/e_gm_test_1. htm 17

Interpretation of hypothesis test • Either something unlikely has happened (having probability p < , where p = P(test statistic has observed or more extreme value | H 0 is correct) or H 0 is not true. • It is conventional to choose a significance level of = 0. 05, but other values may be chosen to minimize the sum of costs of type 1 error (falsely reject H 0) and type 2 error (falsely fail to reject H 0). 18

Neyman-Pearson Lemma • How to minimize Pr(type 2 error), given ? • Answer: Reject H 0 in favor of HA if and only if P(data | HA)/P(data | H 0) > k, for some constant k – The ratio LR = P(data | HA)/P(data | H 0) is called the likelihood ratio – With independent samples, P(data | H) = product of P(xi | H) values for all data points xi – k is determined from . http: //www. aiaccess. net/English/Glossaries/Glos. Mod/e_gm_neyman_pearson. htm 19

Statistical decision theory: Key ideas • Statistical inference from data can be formulated in terms of decision problems • Point estimation: Minimize expected loss from error, given a loss function – Implies using posterior mean if loss function is quadratic (mean squared error) – Implies using posterior median if loss function is absolute value of error • Hypothesis testing: Minimize total expected loss = loss from false positives + loss from false negatives + sampling costs 20

Updating normal distributions 21

Updating normal distributions) • Probability model: N(m, s 2) ; pnorm(x, m, s) • Initial uncertainty about input m is modeled by a normal prior with parameters m 0, s 0 – Prior N(x, m 0, s 0) has mean m 0 • Observe data: x 1 = sample mean of n 1 independent observations • Posterior uncertainty about m: N(m*, s*2), m* = wm 0 + (1 - w)x 1, s* = sqrt(ws 02) • w = (s 2/n 1)/(s 2/n 1 + s 02) = 1/(1 + n 1 s 02/s 2) 22

Bayesian updating of normal distributions (Cont. ) • Posterior uncertainty about m: N(m*, s*2), m* = wm 0 + (1 - w)x 1, s* = sqrt(ws 02) • w = (s 2/n 1)/(s 2/n 1 + s 02) = 1/(1 + n 1 s 02/s 2) • Let’s define an “equivalent sample size, ” n 0, for the prior, as follows: s 02 = s 2/n 0. • Then w = n 0/(n 0 + n 1), posterior is N(m*, s*2) – m* = (n 0 m 0 + n 1 x 1)/(n 0 + n 1) – s* = sqrt(s 2/(n 0 + n 1)) 23

Predictive distributions • How to predict probabilities when the inputs to probability models (p for binom, m and s for pnorm, etc. ), are uncertain? • Answer 1: Find posterior by Bayesian conditioning of prior on data. • Answer 2: Use simulation to sample from distribution of inputs. Calculate conditional probabilities from model, given sampled inputs. Average them to get final probability. 24

Example: Predictive normal distribution • If posterior distribution is N(m*, s*2), then the predictive distribution is N(m*, s 2 + s*2) • Mean is just posterior mean, m* • Total uncertainty (variance) in prediction = sum of variance around the (true but uncertain) mean and variance of the mean 25

Example: Exact vs. simulated predictive normal distributions • Model: N(m, 1) with m ~ N(3, 4) • Exact predictive dist. : N(m*, s 2 + s*2) = N(3, 5) • Simulated predictive dist. : N(2. 99, 5. 077) > m = y = NULL; m = rnorm(10000, 3, 2); mean(m); sd(m)^2; for (j in 1: 10000) {; y[j] = rnorm(1, m[j], 1)}; mean(y); sd(y)^2 [1] 3. 000202 [1] 4. 043804 [1] 2. 993081 [1] 5. 077026 26

Simulation: The main idea • To quantify Pr(outcome), create a model for Pr(outcome | inputs) and Pr(inputs). – Pr(input) = joint probability distribution of inputs • Sample values from Pr(input) – Use rdist • Create indicator variable for outcome – 1 if it occurs on a run, else 0 • Mean value of indicator variable = Pr(outcome) 27

Bayesian inference via simulation: Mary revisited • • • Pr(test is positive | disease) = 0. 95 Pr(test is negative | no disease) = 0. 90 Pr(disease) = 0. 03 Find P(disease | test is positive) Answer from Bayes’ Rule” 0. 2270916 Answer by simulation: # Initialize variables disease_status = test_result_if_disease = test_result_if_no_disease = NULL; n = 100000; # simulate disease state and test outcomes disease_status = rbinom(n, 1, 0. 03); test_result_if_disease = rbinom(n, 1, 0. 95); test_result_if_no_disease = rbinom(n, 1, 0. 10); test_result = disease_status* test_result_if_disease + (1 - disease_status)*test_result_if_no_disease; # calculate and report desired conditional probability sum(disease_status*test_result)/sum(test_result) [1] 0. 2263892 28

Wrap-up on probability models • Highly useful for estimating probabilities in many standard situations – Pr(0 arrivals in h hours) if mean arrival rate is known – Conservative estimates for proportions • Useful for showing uncertainty about probabilities using Bayes’ Rule – Beta posterior distribution for proportions 29

Binomial models for statistical quality control decisions: Sequential and adaptive hypothesis-testing 30

Quality control decisions • Observe data, decide what to do – Intervene in process, accept or reject lot • P-chart for quality control of process – For attributes (pass/fail, conform/not conform) • Lot acceptance sampling – Accept or reject lot based on sample • Adaptive sampling – Sequential probability ratio test (SPRT) 31

“Rule of 3”: Using the binomial model to bound probabilities • If no failures are observed in N binomial trials, then how large might the failure probability be? • Answer: At most 3/N – 95% upper confidence limit – Derivation: If failure probability is p, then the probability of 0 failures in N trials is (1 - p)N. – (1 - p)N > 0. 05 1 - p > 0. 051/N ln(1 - p) > 2. 9957/N -p > -3/N p < 3/N log(1 − x) = 32

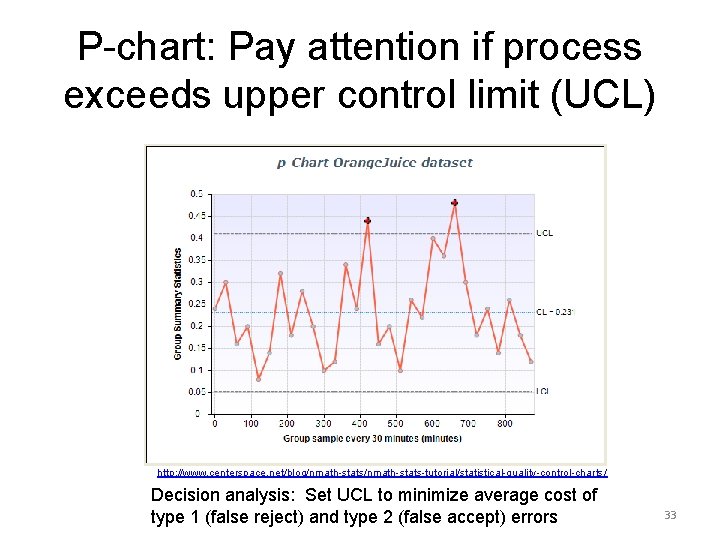
P-chart: Pay attention if process exceeds upper control limit (UCL) http: //www. centerspace. net/blog/nmath-stats-tutorial/statistical-quality-control-charts/ Decision analysis: Set UCL to minimize average cost of type 1 (false reject) and type 2 (false accept) errors 33

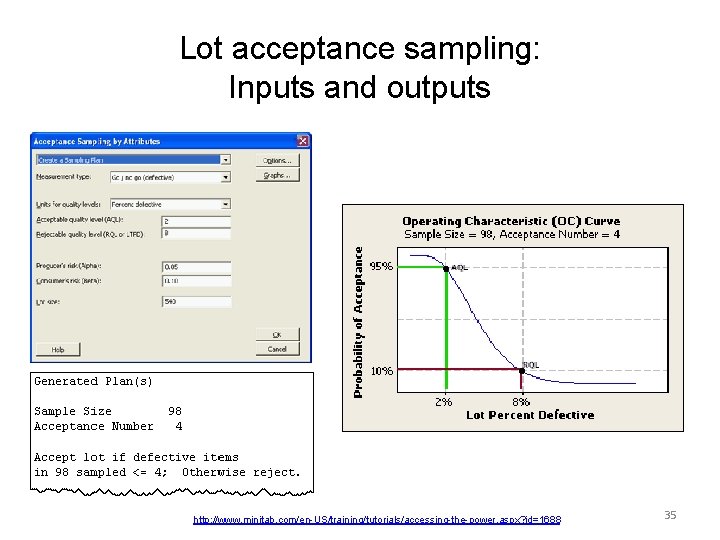
Lot acceptance sampling (by attributes, i. e. , pass/fail inspections) • Take sample of size n • Count non-conforming (fail) items • Accept if number is below threshold; reject if it is above • Optimize choice of n and threshold to minimize expected total costs – Total cost = cost of sampling + cost of erroneous decisions 34

Lot acceptance sampling: Inputs and outputs http: //www. minitab. com/en-US/training/tutorials/accessing-the-power. aspx? id=1688 35

Zero-based acceptance sampling plan calculator Squeglia Zero-Based Acceptance Sampling Plan Calculator Enter your process parameters: Batch/lot size (N) The number of items in the batch (lot). AQL The Acceptable Quality Level. If no AQL is contractually specified, an AQL of 1. 0% is suggested http: //www. sqconline. com/squeglia-zero-based-acceptance-sampling-plan-calculator 36

Zero-based acceptance sampling plan calculator Squeglia Zero-Based Acceptance Sampling Plan (Results) For a lot of 91 to 150 items, and AQL= 10. 0% , the Squeglia zero-based acceptance sampling plan is: Sample 5 items. If the number of non-conforming items is 0 accept the lot 1 reject the lot This plan is based on DCMA (Defense Contract Management Agency) recommendations. http: //www. sqconline. com/squeglia-zero-based-acceptance-sampling-plan-calculator 37

Multi-stage lot acceptance sampling • Take sample of size n • Count non-conforming (fail) items • Accept if number is below threshold 1; reject if it is above threshold 2; sample again if between the thresholds – For single-sample decisions, thresholds 1 and 2 are the same • Optimize choice of n and thresholds to minimize expected total costs 38

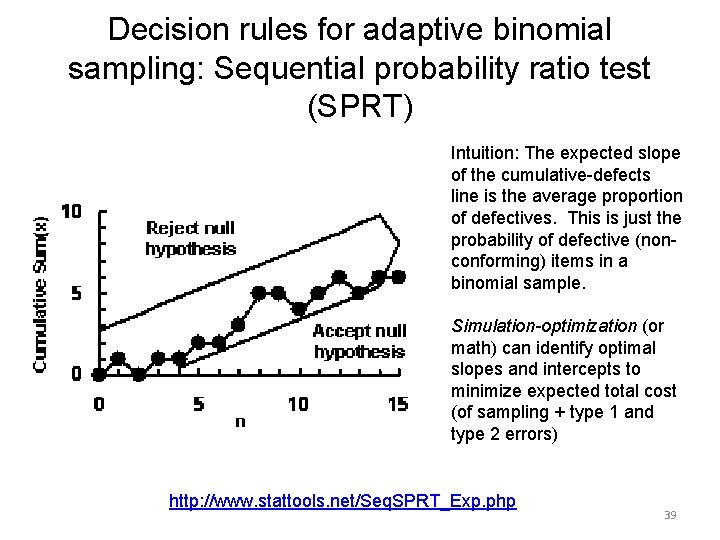
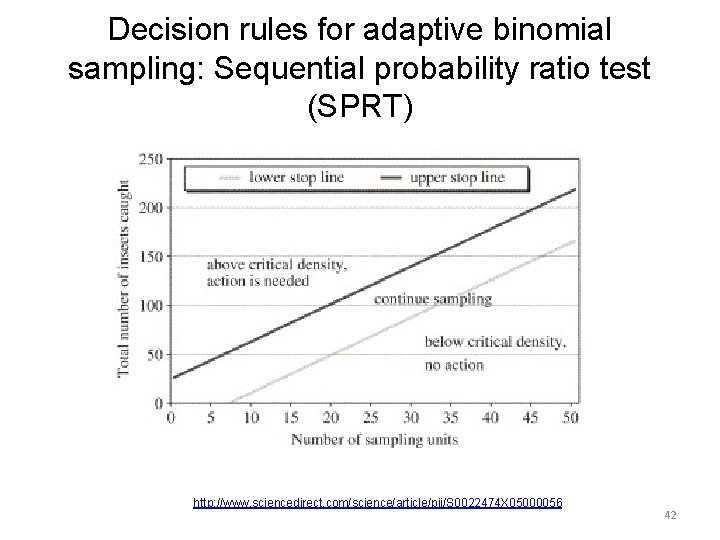
Decision rules for adaptive binomial sampling: Sequential probability ratio test (SPRT) Intuition: The expected slope of the cumulative-defects line is the average proportion of defectives. This is just the probability of defective (nonconforming) items in a binomial sample. Simulation-optimization (or math) can identify optimal slopes and intercepts to minimize expected total cost (of sampling + type 1 and type 2 errors) http: //www. stattools. net/Seq. SPRT_Exp. php 39

Generalizations of SPRT • Main ideas apply to many other (non-binomial) problems • SPRT decision rule: Use data to compute the likelihood ratio LRt = P(ct | HA)/P(ct | H 0). • If LRt > (1 – )/ then stop and reject H 0 • If LRt < / 1 – ) then stop and accept H 0 • Else continue sampling – ct = number of adverse events by time t – H 0 = null hypothesis (process has acceptably small defect rate); H 0 = alternative hypothesis – = false rejection rate for H 0 (type 1 error rate) – = false acceptance rate for H 0 (type 2 error rate) http: //www. tandfonline. com/doi/pdf/10. 1080/07474946. 2011. 539924? no. Frame=true 40

Implementing the SPRT • Optimal slopes and intercepts to achieve different combinations of type 1 and type 2 errors are tabulated. Example application: Testing for mean time to failure (MTTF) of electronic components 41

Decision rules for adaptive binomial sampling: Sequential probability ratio test (SPRT) http: //www. sciencedirect. com/science/article/pii/S 0022474 X 05000056 42

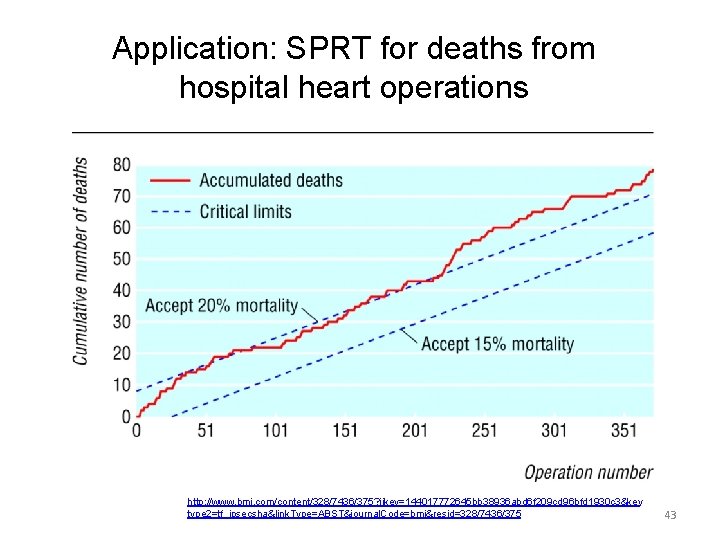
Application: SPRT for deaths from hospital heart operations http: //www. bmj. com/content/328/7436/375? ijkey=144017772645 bb 38936 abd 6 f 209 cd 96 bfd 1930 c 3&key type 2=tf_ipsecsha&link. Type=ABST&journal. Code=bmj&resid=328/7436/375 43

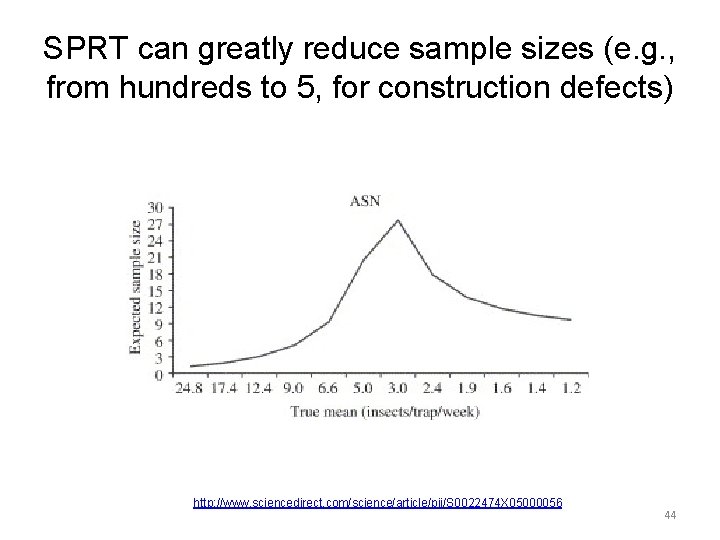
SPRT can greatly reduce sample sizes (e. g. , from hundreds to 5, for construction defects) http: //www. sciencedirect. com/science/article/pii/S 0022474 X 05000056 44

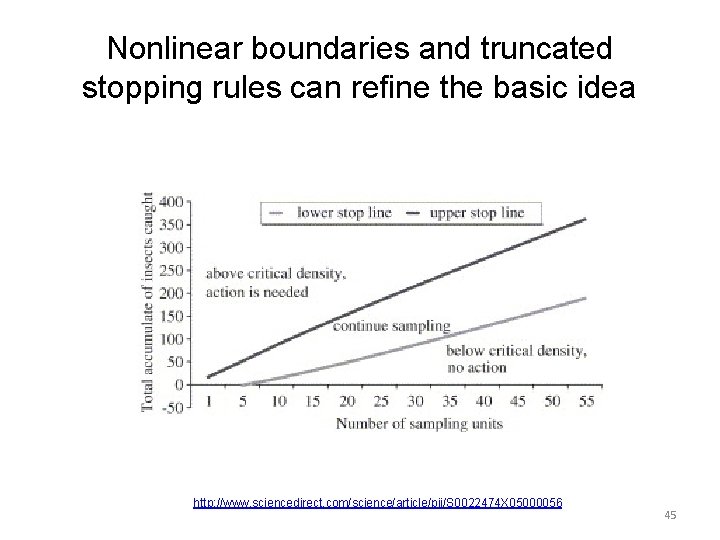
Nonlinear boundaries and truncated stopping rules can refine the basic idea http: //www. sciencedirect. com/science/article/pii/S 0022474 X 05000056 45

Wrap-up on SPRT • Sequential and adaptive sampling can reduce total decision costs (costs of sampling + costs of error) • Computationally sophisticated (and challenging) algorithms have been developed to approximately optimize decision boundaries for statistical decision rules • Adaptive approaches are especially valuable for decisions in uncertain and changing environments. 46

Multi-arm bandits and adaptive learning 47

Multi-arm bandit (MAB) decision problem: Comparing uncertain reward distributions • Multi-arm bandit (MAB) decision problem: On each turn, can select any of k actions – Context-dependent bandit: Get to see a “context” (signal) x before making decision • Receive random reward with (initially unknown) distribution that depends on the selected action • Goal: Maximize sum (or discounted sum) of rewards; minimize regret (= expected difference between best (if distributions were known) and actually received cumulative rewards) http: //jmlr. org/proceedings/papers/v 32/gopalan 14. pdf Gopalan et al. , 2014 https: //jeremykun. com/2013/10/28/optimism-in-the-face-of-uncertainty-the-ucb 1 -algorithm/ 48

MAB applications • Clinical trials: Compare old drug to new. Which has higher success rate? • Web advertising, A/B testing: Which version of a web ad maximizes clickthrough, purchases, etc. ? • Public policies: Which policy best achieves its goals? – Use evidence from early adopter locations to inform subsequent choices 49

Upper confidence bound (UCB 1) algorithm for solving MAB • Try each action once. • For each action a, record average reward m(a) obtained from it so far and how many times it has been tried, n(a). • Let N = an(a) = total number of actions so far. • Choose next the action with the greatest upper confidence bound (UCB): m(a) + sqrt(2*log(N)/n(a)) – Implements “Optimism in the face of uncertainty” principle – UCB for a decreases quickly with n(a), increases slowly with N – Achieves theoretical optimum: logarithmic growth in regret • Same average increase in first 10 plays as in next 90, then next 900, and so on – Requires keeping track each round (not batch updating) Auer et al. , 2002 http: //homes. dsi. unimi. it/~cesabian/Pubblicazioni/ml-02. pdf 50

Thompson sampling and adaptive Bayesian control: Bernoulli trials • Basic idea: Choose each of the k actions according to the probability that it is best • Estimate the probability via Bayes’ rule – It is the mean of the posterior distribution – Use beta conjugate prior updating for “Bernoulli bandit” (0 -1 reward, fail/succeed) S = success F = failure http: //jmlr. org/proceedings/papers/v 23/agrawal 12. pdf Agrawal and Goyal, 2012 51