Decision Analysis Alternatives and States of Nature Good

Decision Analysis • Alternatives and States of Nature • Good Decisions vs. Good Outcomes • Payoff Matrix • Decision Trees • Utility Functions • Decisions under Uncertainty • Decisions under Risk -52 - HMP 654/EXECMAS

Decision Analysis - Payoff Tables Case Problem - (A) p. 38 -53 - HMP 654/EXECMAS

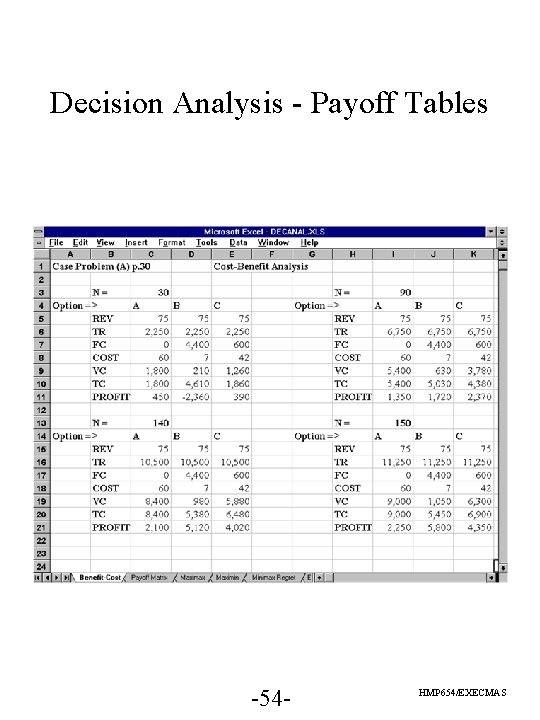
Decision Analysis - Payoff Tables -54 - HMP 654/EXECMAS

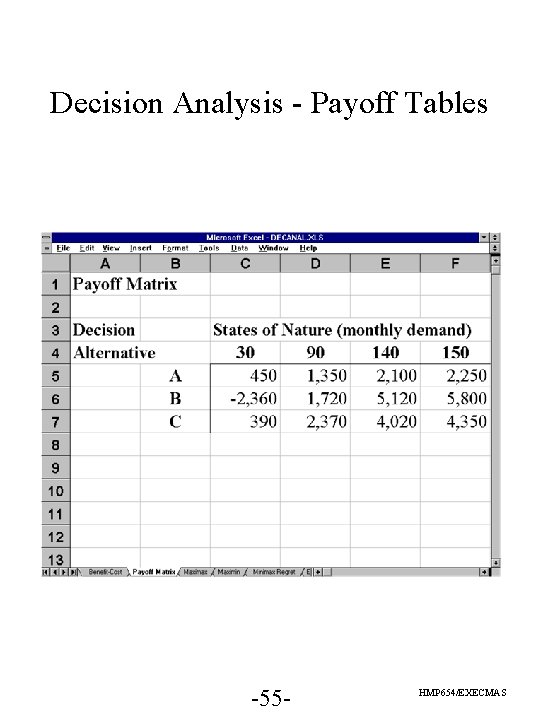
Decision Analysis - Payoff Tables -55 - HMP 654/EXECMAS

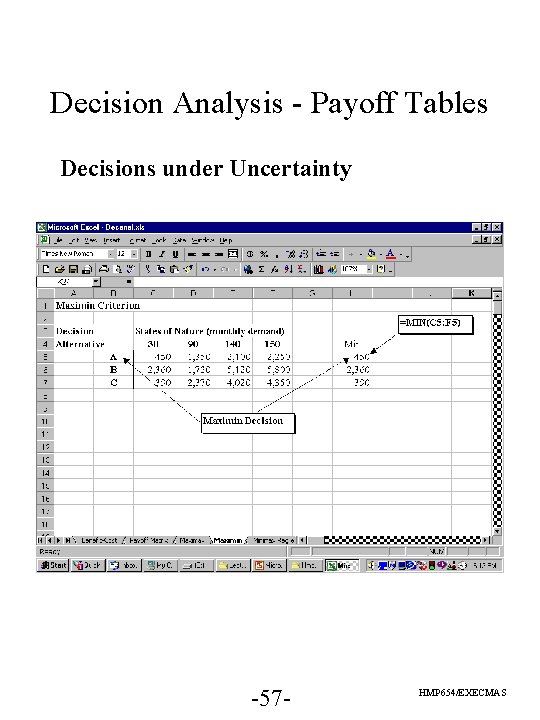
Decision Analysis - Payoff Tables Decisions under Uncertainty -56 - HMP 654/EXECMAS

Decision Analysis - Payoff Tables Decisions under Uncertainty -57 - HMP 654/EXECMAS

Decision Analysis - Payoff Tables Decisions under Uncertainty -58 - HMP 654/EXECMAS

Decision Analysis - Payoff Tables Decisions under Risk -59 - HMP 654/EXECMAS

Decision Analysis - Payoff Tables Decisions under Risk -60 - HMP 654/EXECMAS

Decision Analysis - Payoff Tables Decisions under Risk -61 - HMP 654/EXECMAS

Decision Analysis - Utility Theory • Utility theory provides a way to incorporate the decision maker’s attitudes and preferences toward risk and return in the decision analysis process so that the most desirable decision alternative is identified. • A utility function translates each of the possible payoffs in a decision problem into a nonmonetary measure known as a utility. -62 - HMP 654/EXECMAS

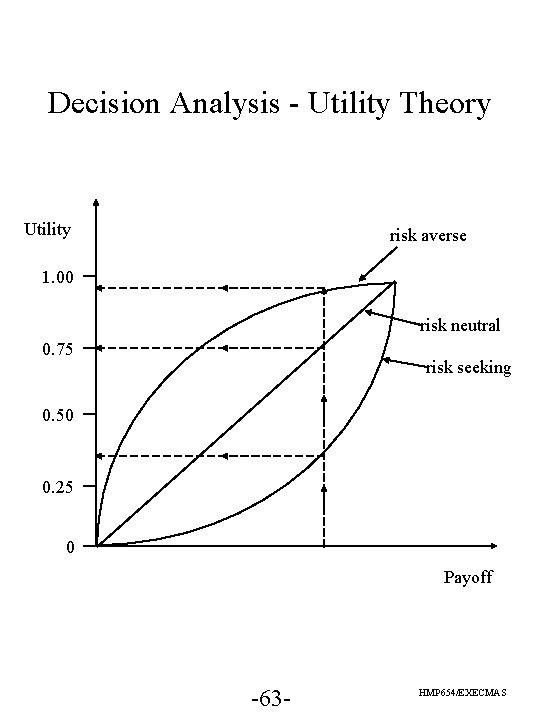
Decision Analysis - Utility Theory Utility risk averse 1. 00 risk neutral 0. 75 risk seeking 0. 50 0. 25 0 Payoff -63 - HMP 654/EXECMAS

Decision Analysis - Utility Theory • The utility of a payoff represents the total worth, value, or desirability of the outcome of a decision alternative to the decision maker. • A risk averse decision maker assigns the largest relative utility to any payoff but has a diminishing marginal utility for increased payoffs. -64 - HMP 654/EXECMAS

Decision Analysis - Utility Theory • A risk seeking decision maker assigns the smallest utility to any payoff but has an increasing marginal utility for increased payoffs. • A risk neutral decision maker falls in between these two extremes and has a constant marginal utility for increased payoffs. -65 - HMP 654/EXECMAS

Decision Analysis - Utility Theory Constructing Utility Functions • Step 1 - Assign a utility value of 0 to the worst outcome (W) in a decision problem and a utility value of 1 to the best outcome (B). -66 - HMP 654/EXECMAS

Decision Analysis - Utility Theory Constructing Utility Functions • Step 2 - For any other outcome x, find the probability p at which the decision maker is indifferent between the following two alternatives: – Receive x with certainty or – Receive B with probability p or W with probability 1 -p The value of p is the utility that the decision maker assigns to the outcome x. -67 - HMP 654/EXECMAS

Decision Analysis - Utility Theory Constructing Utility Functions For example, let’s compute the utility for the $450 entry that corresponds to alternative A and state of nature N=30. The problem consists on finding the value of p that makes the following two options equally attractive for the decision maker: – Receive $450 with certainty – Play a game in which the decision maker can make $5, 800 with probability p or lose $2, 360 with probability 1 -p Let’s assume that the value of p that makes these two choices equally attractive to the decision maker is 0. 7. Then the utility that the decision maker assigns to the $450 is 0. 7. -68 - HMP 654/EXECMAS

Decision Analysis - Utility Theory Constructing Utility Functions -69 - HMP 654/EXECMAS

Decision Analysis - Utility Theory Constructing Utility Functions -70 - HMP 654/EXECMAS

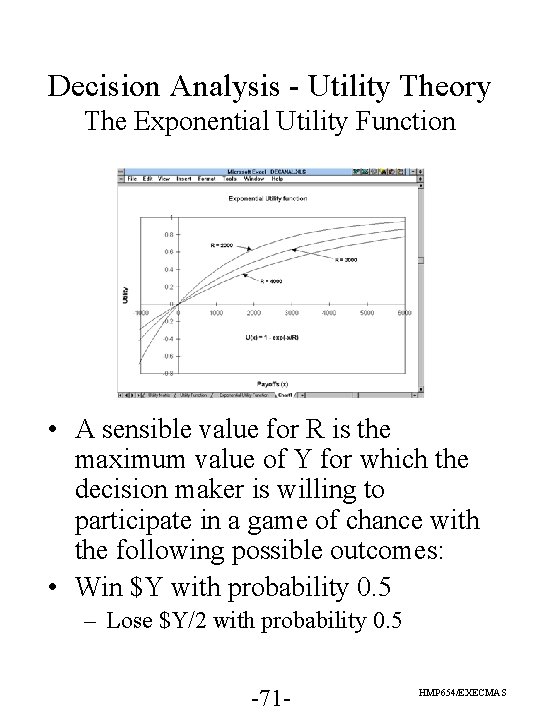
Decision Analysis - Utility Theory The Exponential Utility Function • A sensible value for R is the maximum value of Y for which the decision maker is willing to participate in a game of chance with the following possible outcomes: • Win $Y with probability 0. 5 – Lose $Y/2 with probability 0. 5 -71 - HMP 654/EXECMAS

Decision Analysis - Utility Theory The Exponential Utility Function -72 - HMP 654/EXECMAS