December 2021 Cyclic quadrilaterals LO To solve problems

December 2021 Cyclic quadrilaterals LO: To solve problems using cyclic quadrilaterals theorems. www. mathssupport. org

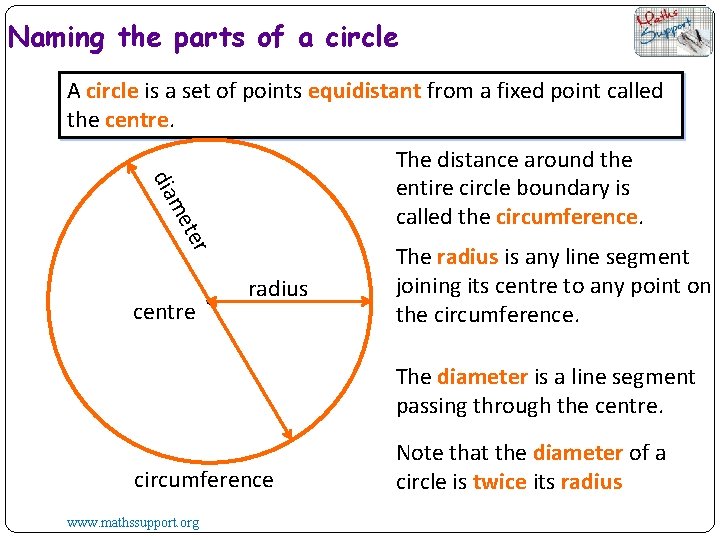
Naming the parts of a circle A circle is a set of points equidistant from a fixed point called the centre. ter me dia The distance around the entire circle boundary is called the circumference. centre radius The radius is any line segment joining its centre to any point on the circumference. The diameter is a line segment passing through the centre. circumference www. mathssupport. org Note that the diameter of a circle is twice its radius

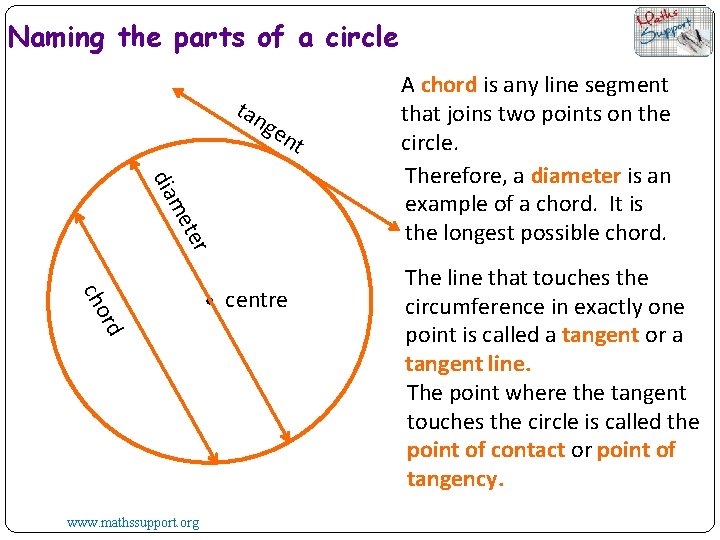
Naming the parts of a circle tan ge nt ter me dia cho rd www. mathssupport. org centre A chord is any line segment that joins two points on the circle. Therefore, a diameter is an example of a chord. It is the longest possible chord. The line that touches the circumference in exactly one point is called a tangent or a tangent line. The point where the tangent touches the circle is called the point of contact or point of tangency.

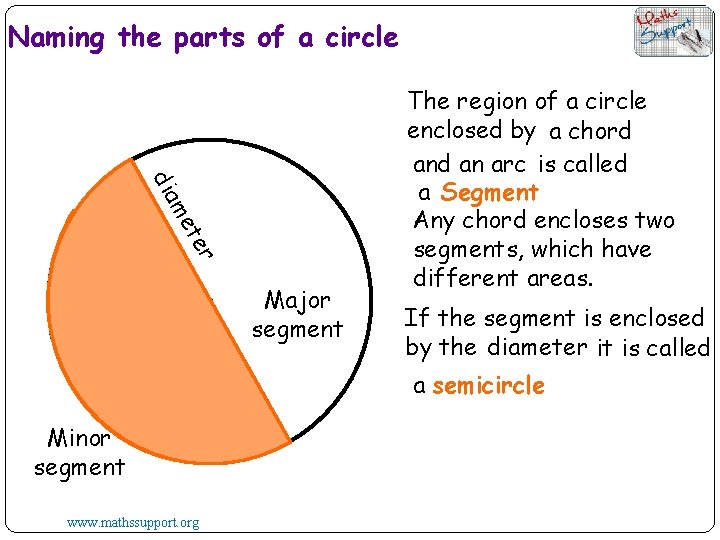
Naming the parts of a circle er t me dia rd cho ent m seg Minor segment www. mathssupport. org Major segment The region of a circle enclosed by a chord an arc is called a Segment Any chord encloses two segments, which have different areas. If the segment is enclosed by the diameter it is called a semicircle

Arcs and sectors arc An arc is any continuous part of the circumference. sector www. mathssupport. org When an arc is bounded a is formed. bysector two radii

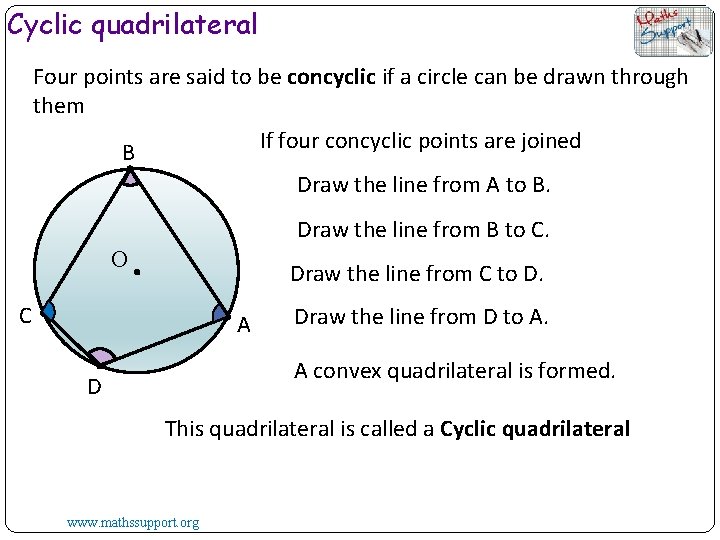
Cyclic quadrilateral Four points are said to be concyclic if a circle can be drawn through them If four concyclic points are joined B Draw the line from A to B. Draw the line from B to C. O Draw the line from C to D. C A Draw the line from D to A. A convex quadrilateral is formed. D This quadrilateral is called a Cyclic quadrilateral www. mathssupport. org

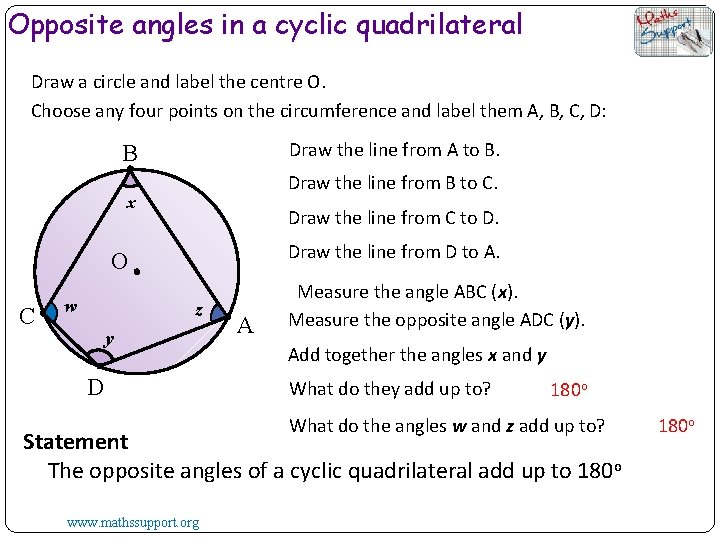
Opposite angles in a cyclic quadrilateral Draw a circle and label the centre O. Choose any four points on the circumference and label them A, B, C, D: Draw the line from A to B. B Draw the line from B to C. x Draw the line from C to D. Draw the line from D to A. O C w z y D A Measure the angle ABC (x). Measure the opposite angle ADC (y). Add together the angles x and y What do they add up to? 180 o What do the angles w and z add up to? Statement The opposite angles of a cyclic quadrilateral add up to 180 o www. mathssupport. org 180 o

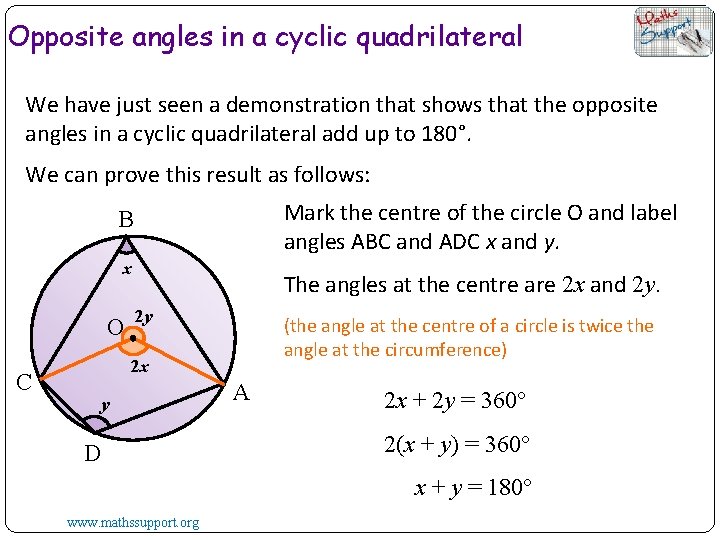
Opposite angles in a cyclic quadrilateral We have just seen a demonstration that shows that the opposite angles in a cyclic quadrilateral add up to 180°. We can prove this result as follows: Mark the centre of the circle O and label angles ABC and ADC x and y. B x O C The angles at the centre are 2 x and 2 y. 2 y (the angle at the centre of a circle is twice the angle at the circumference) 2 x y D A 2 x + 2 y = 360° 2(x + y) = 360° x + y = 180° www. mathssupport. org

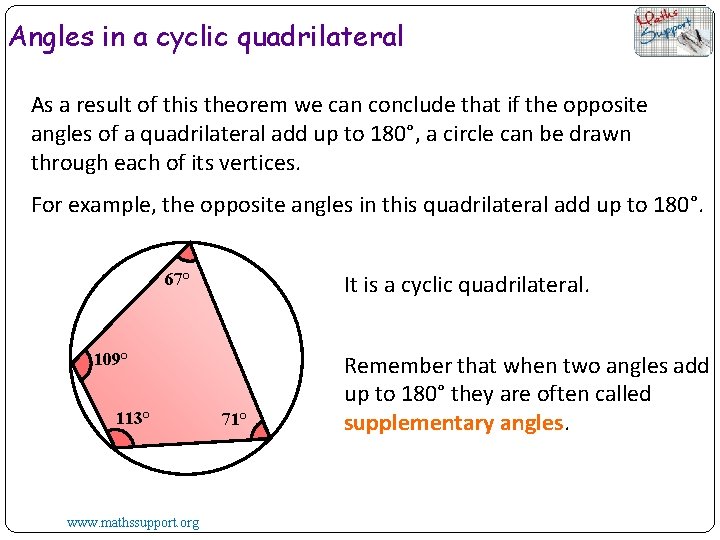
Angles in a cyclic quadrilateral As a result of this theorem we can conclude that if the opposite angles of a quadrilateral add up to 180°, a circle can be drawn through each of its vertices. For example, the opposite angles in this quadrilateral add up to 180°. 67° It is a cyclic quadrilateral. 109° 113° www. mathssupport. org 71° Remember that when two angles add up to 180° they are often called supplementary angles.

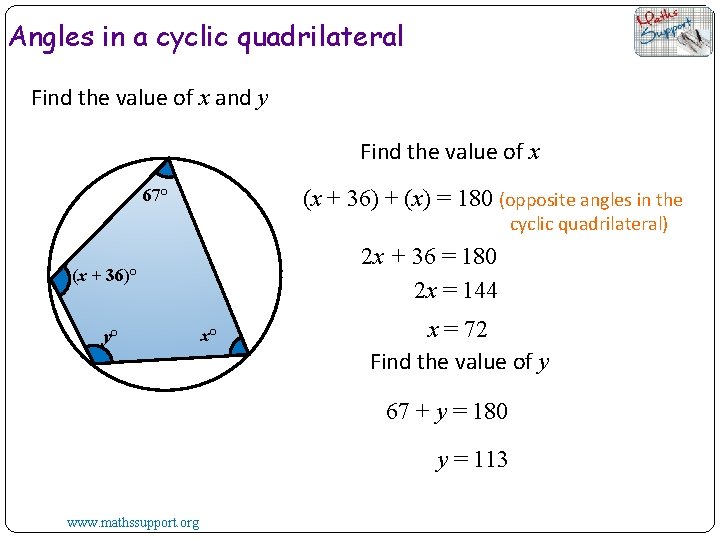
Angles in a cyclic quadrilateral Find the value of x and y Find the value of x (x + 36) + (x) = 180 (opposite angles in the 67° cyclic quadrilateral) 2 x + 36 = 180 2 x = 144 (x + 36)° y° x° x = 72 Find the value of y 67 + y = 180 y = 113 www. mathssupport. org

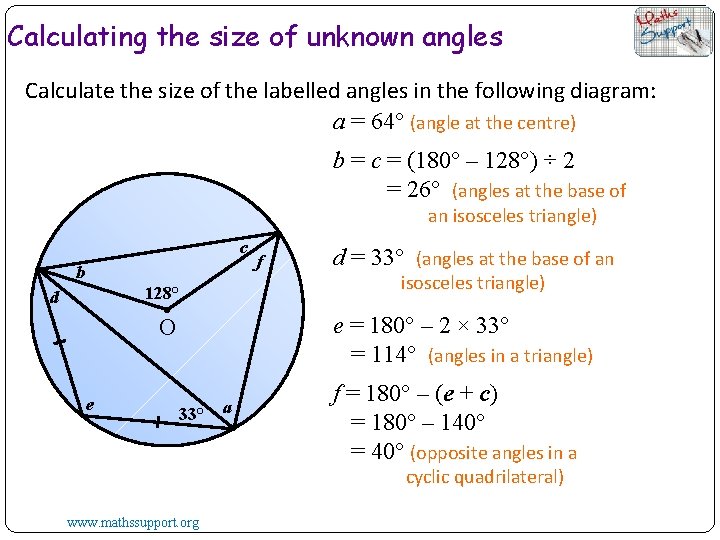
Calculating the size of unknown angles Calculate the size of the labelled angles in the following diagram: a = 64° (angle at the centre) b = c = (180° – 128°) ÷ 2 = 26° (angles at the base of an isosceles triangle) c b 128° d d = 33° (angles at the base of an isosceles triangle) e = 180° – 2 × 33° = 114° (angles in a triangle) O e f 33° a f = 180° – (e + c) = 180° – 140° = 40° (opposite angles in a cyclic quadrilateral) www. mathssupport. org

Thank you for using resources from For more resources visit our website https: //www. mathssupport. org If you have a special request, drop us an email info@mathssupport. org Get 20% off in your next purchase from our website, just use this code when checkout: MSUPPORT_20 www. mathssupport. org