DEBRE MARKOS UNIVERSITY INSTITUTE OF TECHNOLOGY MECHANICAL ENGINEERING

DEBRE MARKOS UNIVERSITY INSTITUTE OF TECHNOLOGY MECHANICAL ENGINEERING DEPARTMENT Instructor; Endalk B. (MSc. . ) Maintenance And installation of machinery 1

Chapter 7 Basic Probability Concepts Introduction üPeople use the term probability many times each day. ü For example, physician says that a persevering has a 50 -50 chance of surviving a certain operation. ü Another technicians may say that the machine is 95% that a machine has a particular failure. 2

Definition Experiment = any planned process of data collection. It consists of a number of trials (replications) under the same condition. • Sample space: collection of unique, non-overlapping possible outcomes of a random circumstance. • Simple event: one outcome in the sample space; a possible outcome of a random circumstance. • Event: a collection of one or more simple events in the sample space; often written as A, B, C, and so on. Male, Female 3

Cont. Complement = sometimes, we want to know the probability that an event will not happen; an event opposite to the event of interest is called a complementary event. If A is an event, its complement is The probability of the complement is AC or A Example: The complement of male event is the female. P(A) + P(AC) = 1 4

Probability: is a chance of occurrence of an events , but question of a chance is because of uncertainty. • Joint probability ? • Marginal probability ? • Conditional probability ? 5

Problem 1. An outbreak of not functional occurs in a group of machines who attended in maintenance shop Find the probability of not functional and applied lubricant Not functional Total lubricated Did Not lubricated 90 20 30 60 120 80 Total 110 90 200 6

The joint probability of not functional and applied lubricant P(not functional) = 110/200 = 0. 55 P(not functionalapplied lubricant) = 90/120 = 0. 75 ØThen the two events are dependent P(not functional ∩ applied lubricant) = P(applied lubricant) P(not functional P(applied lubricant) = (120/200) (90/120) = 0. 45 7

Properties The probability ranges between 0 and 1 If an outcome cannot occur, its probability is 0 If an outcome is sure, it has a probability of 1 The sum of probabilities of mutually exclusive outcomes is equal to 1 P(M) + P(F) = 1 8

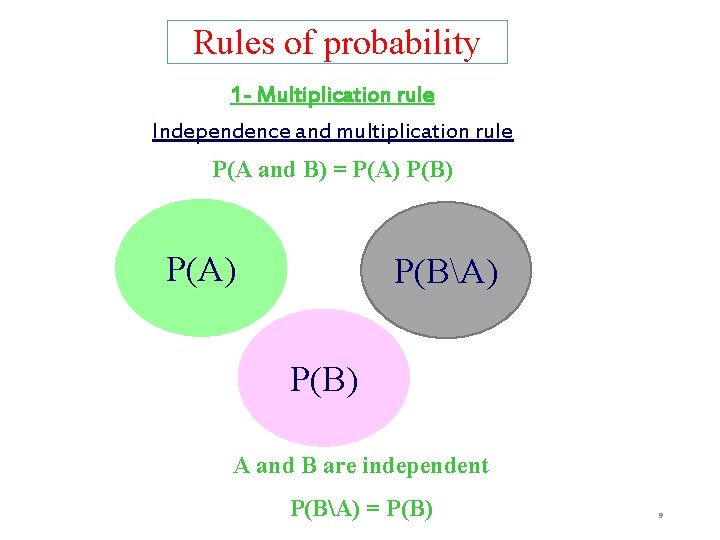
Rules of probability 1 - Multiplication rule Independence and multiplication rule P(A and B) = P(A) P(B) P(A) P(BA) P(B) A and B are independent P(BA) = P(B) 9

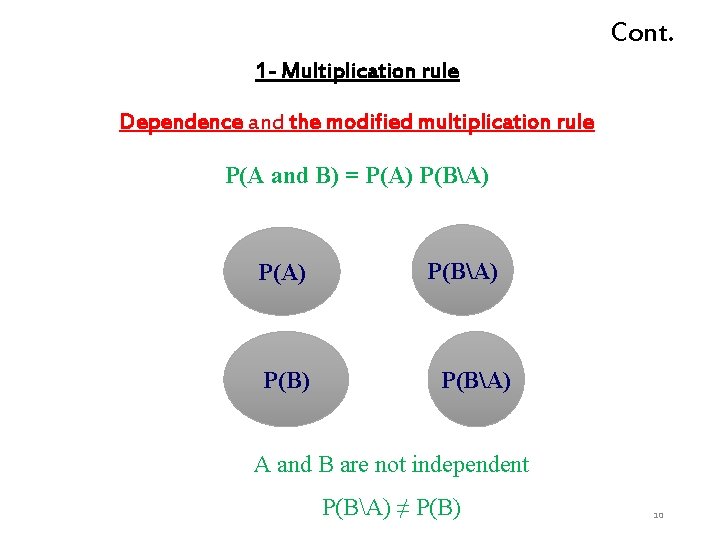
Cont. 1 - Multiplication rule Dependence and the modified multiplication rule P(A and B) = P(A) P(BA) P(B) P(BA) A and B are not independent P(BA) ≠ P(B) 10

2 - Addition rule i) A and B are mutually exclusive, The occurrence of one event precludes the occurrence of the other Addition Rule P(A) P(B) P(A OR B) = P(A U B) = P(A) + P(B) 11

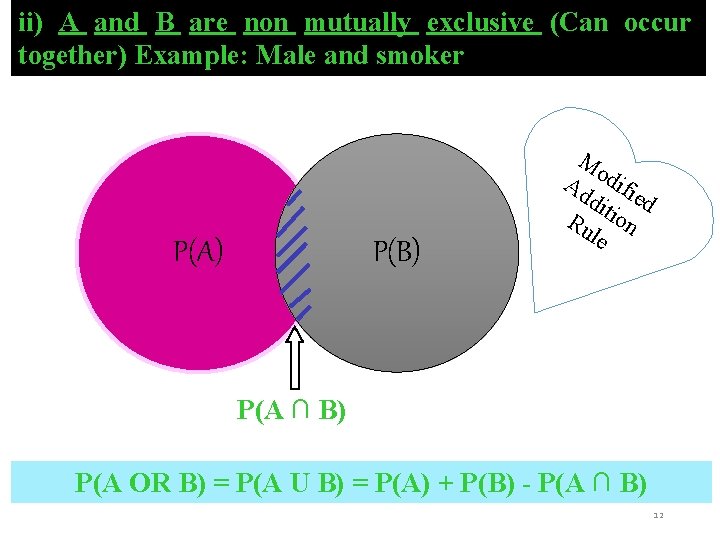
ii) A and B are non mutually exclusive (Can occur together) Example: Male and smoker P(A) P(B) Mo Ad difi dit ed Ru ion le P(A ∩ B) P(A OR B) = P(A U B) = P(A) + P(B) - P(A ∩ B) 12