DEADLOCK Process Manager Review Program Process Abstract Computing

DEADLOCK
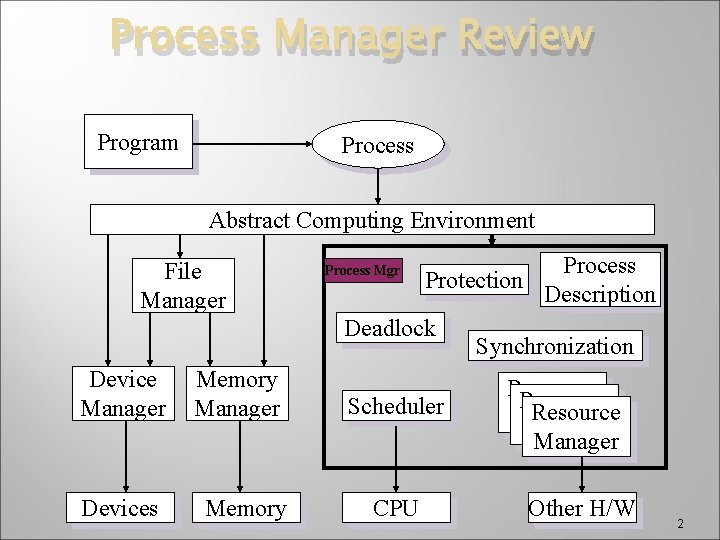
Process Manager Review Program Process Abstract Computing Environment File Manager Process Mgr Protection Deadlock Device Manager Devices Memory Manager Memory Scheduler CPU Process Description Synchronization Resource Manager Other H/W 2

Introduction �Let S and Q be two semaphores initialized to 1 P 0 P 1 P(S); P(Q); P(S); V(Q); V(Q) V(S); � What is the potential problem? � How could we overcome this problem if we want to have least constraints on the programmers? 3

Deadlocks - Introduction � Kansas State legislature � “When two trains approach each other at a crossing, both shall come to a full stop and neither shall start up again until the other is gone” 4

Bridge Crossing Example � � � Traffic only in one direction. Each section of a bridge can be viewed as a resource. If a deadlock occurs, it can be resolved if one car backs up (preempt resources and rollback). Several cars may have to be backed up if a deadlock occurs. Starvation is possible. 5
Automobile Gridlocks 6

The Deadlock Problem � � A set of blocked processes each holding a resource and waiting to acquire a resource held by another process in the set. Example � System has 2 tape drives, one CD-ROM and one DAT drive. � P 1 and P 2 each hold one tape drive and each needs another one. 7
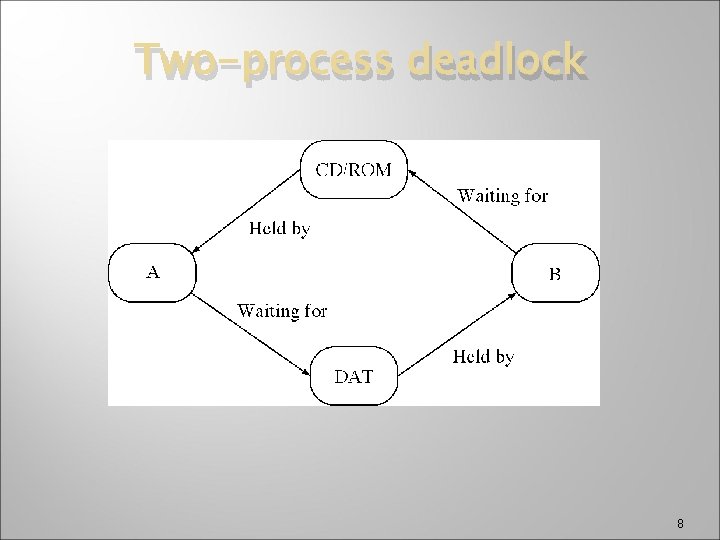
Two-process deadlock 8

Deadlock Examples � Semaphore example � semaphores P 0 P(A); P(B); � – cont. A and B, initialized to 1 P(B); P(A); Message deadlock example � Process A { receive(B, msg); send(B, msg): } � Process B { receive(A, msg); send(A, msg): } � Could result from a message being lost 9
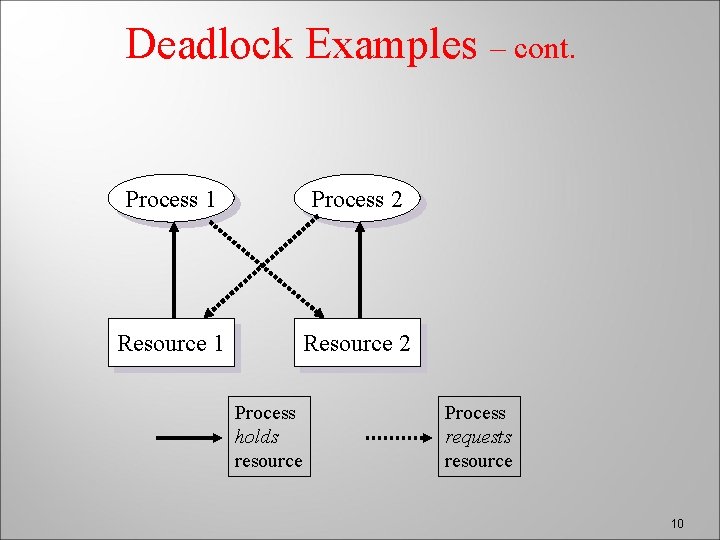
Deadlock Examples – cont. Process 1 Process 2 Resource 1 Resource 2 Process holds resource Process requests resource 10
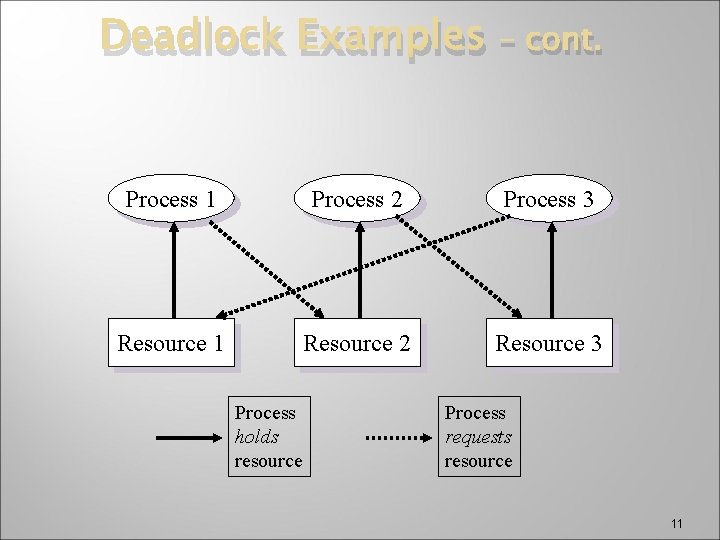
Deadlock Examples – cont. Process 1 Process 2 Process 3 Resource 1 Resource 2 Resource 3 Process holds resource Process requests resource 11
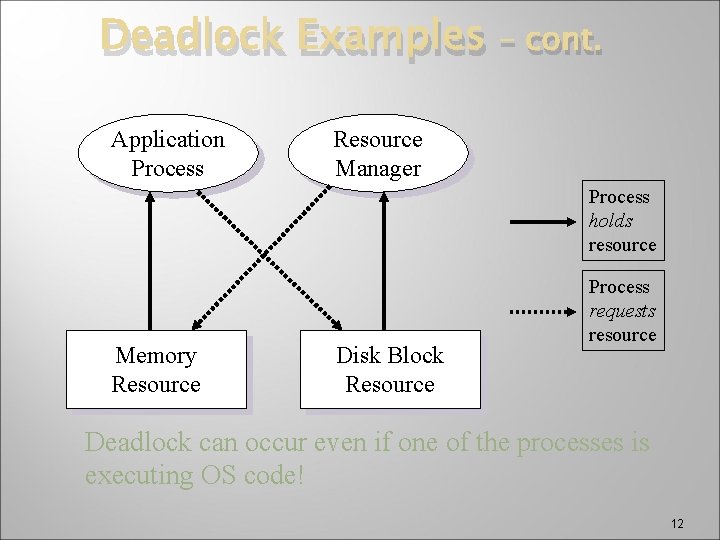
Deadlock Examples Application Process – cont. Resource Manager Process holds resource Memory Resource Disk Block Resource Process requests resource Deadlock can occur even if one of the processes is executing OS code! 12

Deadlock Characterization � Deadlock can arise if four conditions hold simultaneously � Mutual exclusion � Hold and wait: � No preemption � Circular wait 13

Deadlock Characterization � Mutual exclusion � � only one process at a time can use a resource. Hold and wait: �a process holding at least one resource is waiting to acquire additional resources held by other processes. 14

� Deadlock Characterization No preemption �a resource can be released only voluntarily by the process holding it, after that process has completed its task. � Circular wait � there exists a set {P 0, P 1, …, Pn} of waiting processes such that P 0 is waiting for a resource that is held by P 1, P 1 is waiting for a resource that is held by P 2, …, Pn– 1 is waiting for a resource that is held by Pn, and Pn is waiting for a resource that is held by P 0. 15

A Model � � P = {p 1, p 2, …, pn} be a set of processes R = {R 1, R 2, …, Rm} be a set of resources cj = number of units of Rj in the system S = {S 0, S 1, …} be a set of states representing the assignment of Rj to pi � State changes when processes take action � This allows us to identify a deadlock situation in the operating system 16

Resources Resource: Anything that a process can request, then be blocked because that thing is not available. R = {Rj | 0 j < m} = resource types C = {cj 0 | Rj R (0 j < m)} = units of Rj available Reusable resource: After a unit of the resource has been allocated, it must ultimately be released back to the system. E. g. , CPU, primary memory, disk space, … The maximum value for cj is the number of units of that resource Consumable resource: There is no need to release a resource after it has been acquired. E. g. , a message, input data, … Notice that cj is unbounded. 17
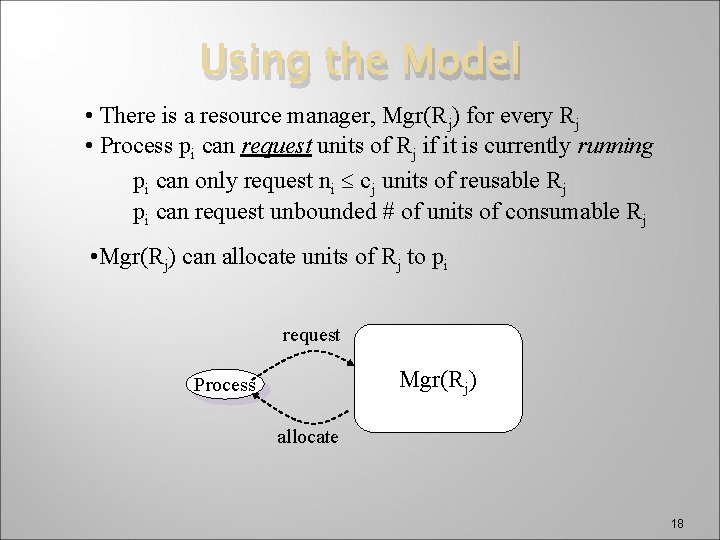
Using the Model • There is a resource manager, Mgr(Rj) for every Rj • Process pi can request units of Rj if it is currently running pi can only request ni cj units of reusable Rj pi can request unbounded # of units of consumable Rj • Mgr(Rj) can allocate units of Rj to pi request Mgr(Rj) Process allocate 18
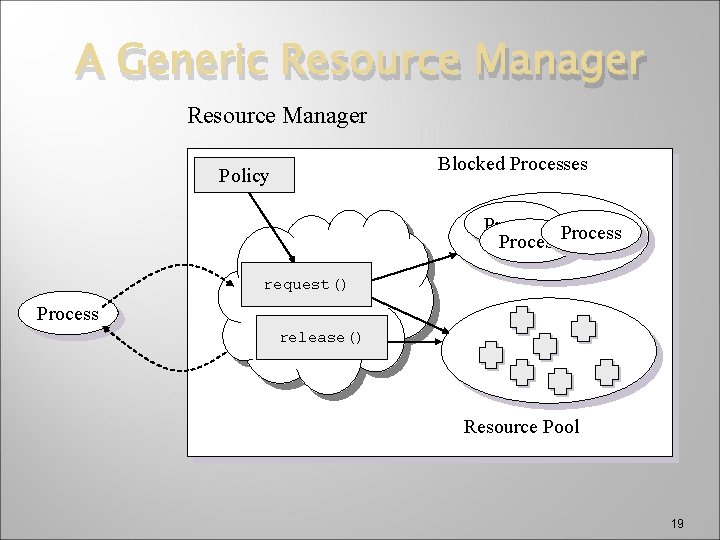
A Generic Resource Manager Blocked Processes Policy Process request() Process release() Resource Pool 19

Using the Model � – cont. In most cases, we assume that each process utilizes a resource as follows � request If the requested resources are not available, the calling process will be blocked � use � release � Which implies that we are dealing with reusable resources 20

State Transitions � � The system changes state because of the action of some process, pi There are three pertinent actions: � Request (“ri”): request one or more units of a resource � Allocation (“ai”): All outstanding requests from a process for a given resource are satisfied � Deallocation (“di”): The process releases units of a resource Sj xi Sk 21

Properties of States � � Want to define deadlock in terms of patterns of transitions Define: pi is blocked in Sj if pi cannot cause a transition out of Sj a 1 Sj r 3 r 1 p 2 is blocked in Sj 22

State Diagram � � If pi is blocked in Sj, and will also be blocked in every Sk reachable from Sj, then pi is deadlocked Sj is called a deadlock state 23
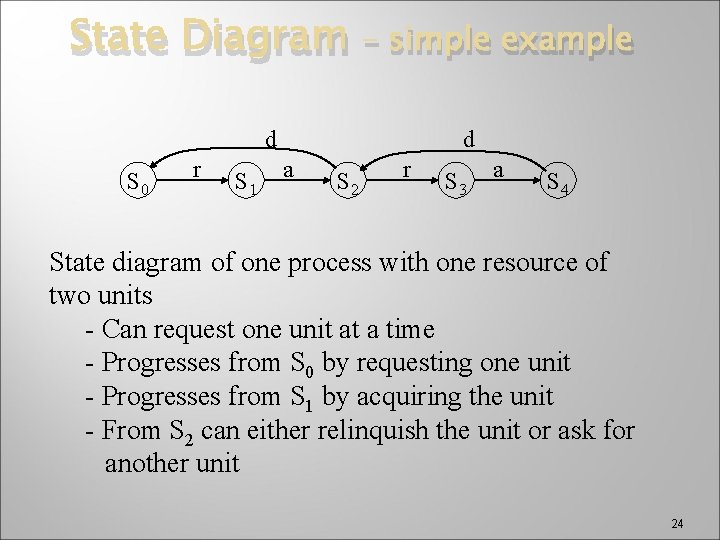
State Diagram – simple example d S 0 r S 1 d a S 2 r S 3 a S 4 State diagram of one process with one resource of two units - Can request one unit at a time - Progresses from S 0 by requesting one unit - Progresses from S 1 by acquiring the unit - From S 2 can either relinquish the unit or ask for another unit 24

State Diagram – example � � Extend this to two processes competing for two units of the single resource type Process may request only one unit at a time State diagram in previous slide must be replicated and copies combined to describe all the system states Those states not possible have been removed 25
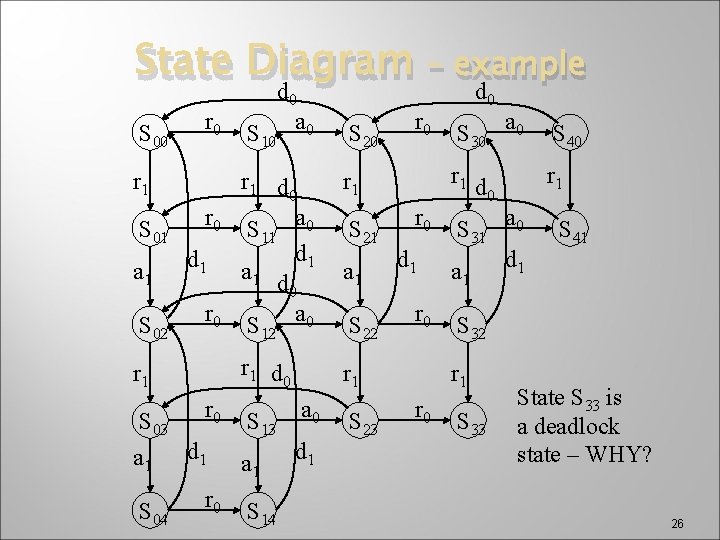
State Diagram d S 00 r 1 S 01 a 1 S 02 r 0 d 1 r 0 r 1 r 0 S 03 a 1 d 1 S 04 r 0 0 S 10 a 0 S 20 r 1 d 0 S 11 a 0 d 1 a 1 d 0 S a 0 r 1 d 0 r 1 12 S 13 a 1 S 14 a 0 d 1 S 21 a 1 S 22 S 23 – example r 0 d 1 r 0 d 0 S 30 a 0 S 40 r 1 d 0 r 1 S 31 a 0 d 1 a 1 S 32 r 1 r 0 S 41 S 33 State S 33 is a deadlock state – WHY? 26

Dealing with Deadlocks � Three ways � Prevention place restrictions on resource requests to make deadlock impossible � Avoidance plan ahead to avoid deadlock. � Recovery Check for deadlock (periodically or sporadically) and recover from it � Manual intervention (the ad hoc approach) Reboot the machine if it seems too slow 27

Deadlock Prevention � Necessary conditions for deadlock � Mutual exclusion � Hold and wait � Circular waiting � No preemption � Ensure that at least one of the necessary conditions is false at all times 28

Mutual Exclusion � � Not required for sharable resources MUST hold for nonsharable resources 29

Hold and Wait � � Need to be sure a process does not hold one resource while requesting another Approach 1: Force a process to request all resources it needs at one time Approach 2: If a process needs to acquire a new resource, it must first release all resources it holds, then reacquire all it needs What does this say about state transition diagrams? 30
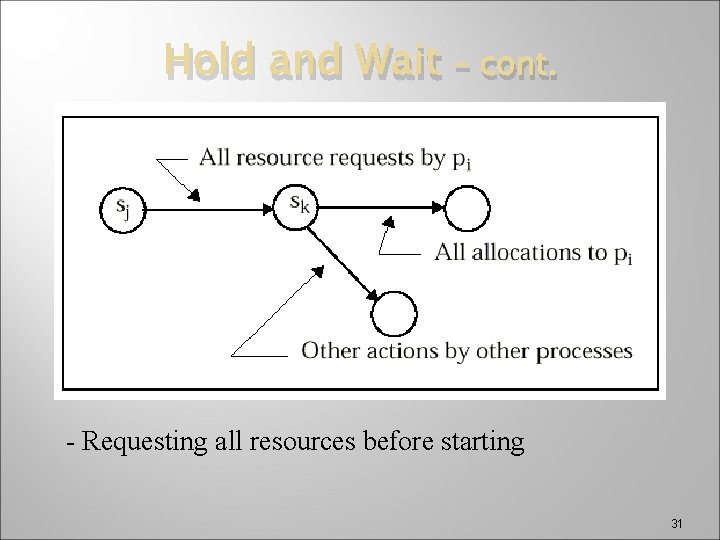
Hold and Wait – cont. - Requesting all resources before starting 31

Hold and Wait – cont. - Release of all resources before requesting more 32

Hold and Wait � – cont. No Preemption – � If a process that is holding some resources requests another resource that cannot be immediately allocated to it, then all resources currently being held are released. � Preempted resources are added to the list of resources for which the process is waiting. � Process will be restarted only when it can regain its old resources, as well as the new ones that it is requesting. 33

Hold and Wait � � – cont. Results in poor utilization of resources Can lead to starvation due to resource unavailability 34

Circular Wait � Occurs when a set of n processes that hold units of a set of n different resources � Impose a total ordering of all resource types, and require that each process requests resources in an increasing order of enumeration � Semaphore example semaphores A and B, initialized to 1 P 0 wait (A); wait (B); P 1 wait(A) wait(B) 35
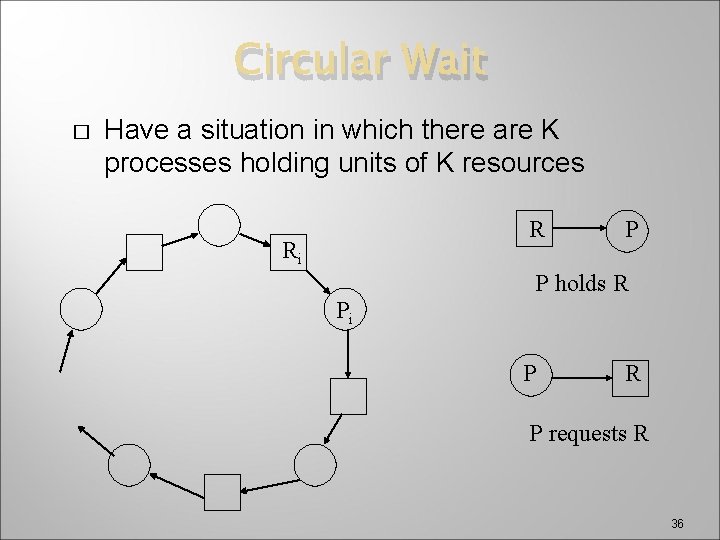
Circular Wait � Have a situation in which there are K processes holding units of K resources R Ri P P holds R Pi P R P requests R 36

Circular Wait � � � – cont. There is a cycle in the graph of processes and resources Choose a resource request strategy by which no cycle will be introduced Total order on all resources, then can only ask for Rj if Ri < Rj for all Ri the process is currently holding 37

Circular Wait � – cont. Implementing this strategy � Require that each process requests resources in an increasing order of the associated numbers A process can request instances of type Ri initially After that, the process can only request instances of resource type Rj if F(Rj) > F(Ri), where F(Ri) and F(Rj) are the associated integer number �It several instances of the same resource type are needed, all of them must be requested in a single request 38

Circular Wait � – cont. Implementation – continued � Whenever a process requests an instance of resource type Rj, it must first release all the resources Ri, such that F(Ri) F(Rj) � Circular wait cannot hold if a total ordering is imposed � Can be shown by contradiction 39

Circular Wait � – cont. This is how we noticed an easy solution for the dining philosophers problem � Put a total order on all forks � Require that philosopher 4 become a “left-handed” philosopher (pick up the forks in a different order than the rest) 40
![Circular Wait philosopher(int i) { while (TRUE) {. . . /* Thinking P(fork[i]); P(fork[(i+1) Circular Wait philosopher(int i) { while (TRUE) {. . . /* Thinking P(fork[i]); P(fork[(i+1)](http://slidetodoc.com/presentation_image_h2/1c9da34d1ee354d532930d54d2e13ef7/image-41.jpg)
Circular Wait philosopher(int i) { while (TRUE) {. . . /* Thinking P(fork[i]); P(fork[(i+1) eat(); V(fork[(i+1) V(fork[i]); } } philosopher 4() { while (TRUE) {. . . /* Thinking P(fork[0]); P(fork[4]; eat(); V(fork[4]; V(fork[0]); } } – cont. */ mod 5]; /* Pick up left fork */ /* Pick up right fork */ mod 5]; */ /* Pick up right fork */ /* Pick up left fork */ 41

Allowing Preemption � Allow a process to time-out on a blocked request -- withdrawing the request if it fails �r = request resource � w = withdraw request � d = release or deallocate resource ru Si dv wu Sk Sj ru 42

Allowing Preemption � – cont. No guarantee that this technique will be effective � System may come to set of states where a set of processes is polling for resources held by other processes in the set � Livelock, since there are transitions in the state diagram (so no deadlock), but none of these transitions are effective in the long run 43

Avoidance � � � Define a model of system states, then choose a strategy that will guarantee that the system will not go to a deadlock state Requires extra information, e. g. , the maximum claim for each process Allows resource manager to see the worst case that could happen, then to allow transitions based on that knowledge 44

Deadlock Avoidance � � Requires that the system has some additional a priori information available Simplest and most useful model requires that each process declare the maximum number of resources of each type that it may need The deadlock-avoidance algorithm dynamically examines the resource-allocation state to ensure that there can never be a circular-wait condition Resource-allocation state is defined by the number of available and allocated resources, and the maximum demands of the processes 45

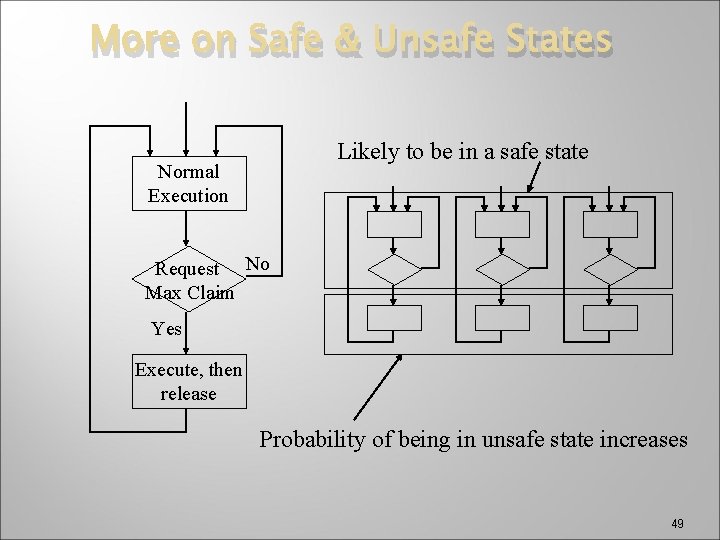
Safe State � � � When a process requests an available resource, system must decide if immediate allocation leaves the system in a safe state. System is in safe state if there exists a safe sequence of all processes. Sequence <P 1, P 2, …, Pn> is safe if for each Pi, the resources that Pi can still request can be satisfied by currently available resources + resources held by all the Pj, with j < i. If Pi resource needs are not immediately available, then Pi can wait until all Pj have finished. � When Pj is finished, Pi can obtain needed resources, execute, return allocated resources, and terminate. � When Pi terminates, Pi+1 can obtain its needed resources, and so on. � 46

Basic Facts � � � If a system is in safe state no deadlocks. If a system is in unsafe state possibility of deadlock. Avoidance ensure that a system will never enter an unsafe state. 47

Comments on Safe State � It is a worst case analysis � If every process were to request its maximum claim, there would be a sequence of allocations and deallocations that could enable the system to satisfy every process’s request in some order � It does not mean that the system must have enough resources to simultaneously meet all the maximum claims 48
More on Safe & Unsafe States Likely to be in a safe state Normal Execution Request No Max Claim Yes Execute, then release Probability of being in unsafe state increases 49
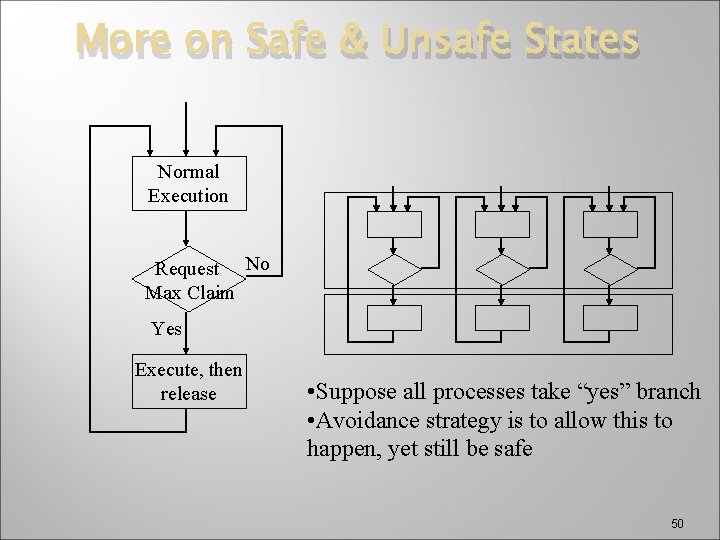
More on Safe & Unsafe States Normal Execution Request No Max Claim Yes Execute, then release • Suppose all processes take “yes” branch • Avoidance strategy is to allow this to happen, yet still be safe 50
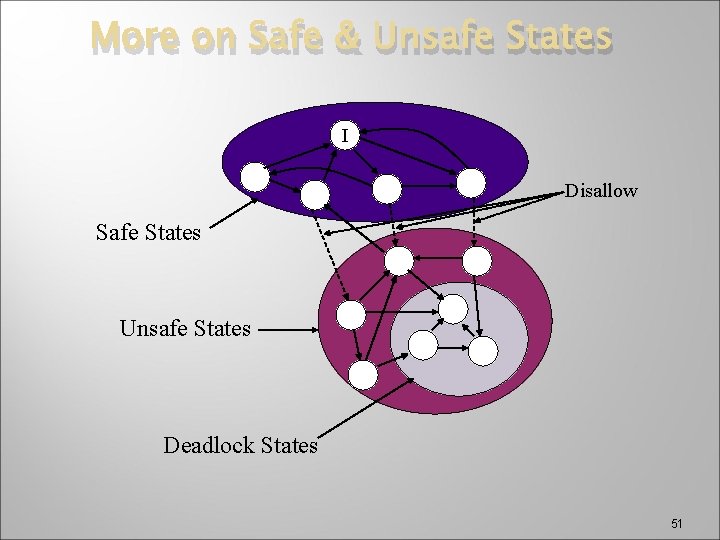
More on Safe & Unsafe States I Disallow Safe States Unsafe States Deadlock States 51

More on Safe & Unsafe States � Note that a system could run in an unsafe state yet not enter a deadlock state � The system may not be able to guarantee that every process could execute its maximum claim, but some processes may not ask for their maximum until the system returns to a safe state, hence avoiding a deadlock � An unsafe state does not mean the system is in deadlock or even close – it merely means the resource manager cannot guarantee anything, and the resulting states will be determined only by the actions of the processes 52

Banker’s Algorithm � � � Best known of avoidance strategies Modeled after lending policies used by banks Each new process entering system declares the maximum use of resources it may need. When a process requests a resource it may have to wait (until system in a safe state). When a process gets all its resources it must return them in a finite amount of time. 53

Data Structures for the Banker’s Algorithm Let n = number of processes, and m = number of resources types. � Available � � Max � � n x m matrix. If Max [i, j] = k, then process Pi may request at most k instances of resource type Rj. Allocation � � Vector of length m. If available [j] = k, there are k instances of resource type Rj available. n x m matrix. If Allocation[i, j] = k then Pi is currently allocated k instances of Rj. Need � n x m matrix. If Need[i, j] = k, then Pi may need k more instances of Rj to complete its task. Need [i, j] = Max[i, j] – Allocation [i, j] 54

Safety Algorithm 1. Let Work and Finish be vectors of length m and n, respectively. Initialize: Work : = Available Finish [i] = false for i - 1, 2, 3, …, n. 2. Find an i such that both: (a) Finish [i] = false (b) Needi Work If no such i exists, go to step 4. 3. Work : = Work + Allocationi Finish[i] : = true go to step 2. 4. If Finish [i] = true for all i, then the system is in a safe state. 55

Example of Banker’s Algorithm � 5 processes P 0 through P 4; 3 resource types A (10 instances), B (5 instances), and C (7 instances). � Snapshot at time T 0: Allocation Max Available ABC ABC P 0 0 1 0 753 332 P 1 2 0 0 322 P 2 3 0 2 902 P 3 2 1 1 222 P 4 0 0 2 4 3 3 56
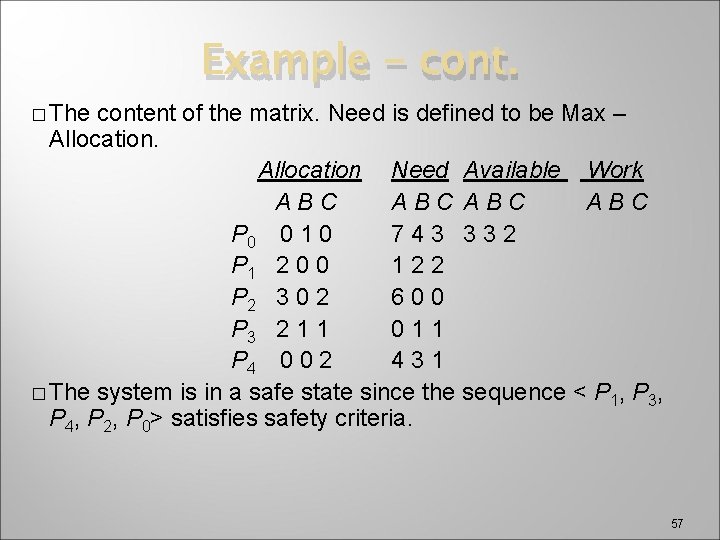
Example - cont. � The content of the matrix. Need is defined to be Max – Allocation Need Available Work ABC ABC P 0 0 1 0 743 332 P 1 2 0 0 122 P 2 3 0 2 600 P 3 2 1 1 011 P 4 0 0 2 431 � The system is in a safe state since the sequence < P 1, P 3, P 4, P 2, P 0> satisfies safety criteria. 57

Resource-Request Algorithm for Process Pi Requesti = request vector for process Pi. If Requesti [j] = k then process Pi wants k instances of resource type Rj. 1. If Requesti Needi go to step 2. Otherwise, raise error condition, since process has exceeded its maximum claim. 2. If Requesti Available, go to step 3. Otherwise Pi must wait, since resources are not available. 3. Pretend to allocate requested resources to Pi by modifying the state as follows: Available : = Available – Requesti; Allocationi : = Allocationi + Requesti; Needi : = Needi – Requesti; ; If safe the resources are allocated to Pi. If unsafe Pi must wait, and the old resource-allocation state is restored 58

Example: P 1 request (1, 0, 2) � Check that Request Available (that is, (1, 0, 2) (3, 3, 2) true. ) Allocation Need Available ABC ABC P 0 0 1 0 743 230 P 1 3 0 2 020 P 2 3 0 2 600 P 3 2 1 1 011 P 4 0 0 2 431 � Executing safety algorithm shows that sequence <P 1, P 3, P 4, P 0, P 2> satisfies safety requirement. 59

Example Continued Allocation Need Available ABC ABC P 0 0 1 0 743 230 P 1 3 0 2 020 P 2 3 0 2 600 P 3 2 1 1 011 P 4 0 0 2 431 � Can an additional request for (3, 3, 0) by P 4 be granted? � Can an additional request for (0, 2, 0) by P 0 be granted? 60
![Banker’s Algorithm Assume n processes and m resources: � � Let maxc[i, j] be Banker’s Algorithm Assume n processes and m resources: � � Let maxc[i, j] be](http://slidetodoc.com/presentation_image_h2/1c9da34d1ee354d532930d54d2e13ef7/image-61.jpg)
Banker’s Algorithm Assume n processes and m resources: � � Let maxc[i, j] be the maximum claim for Rj by pi Let alloc[i, j] be the number of units of Rj held by pi Let ci be the number of units of each resource Ri Can always compute = cj - S 0 i< nalloc[i, j] � The number of available units of Rj � avail[j] � Should be able to determine if the state is safe or not using this info 61
![Banker’s Algorithm 1. 2. 3. – cont. Copy the alloc[i, j] table to alloc’[i, Banker’s Algorithm 1. 2. 3. – cont. Copy the alloc[i, j] table to alloc’[i,](http://slidetodoc.com/presentation_image_h2/1c9da34d1ee354d532930d54d2e13ef7/image-62.jpg)
Banker’s Algorithm 1. 2. 3. – cont. Copy the alloc[i, j] table to alloc’[i, j] Given C, maxc and alloc’, compute avail vector Find pi such that maxc[i, j] - alloc’[i, j] avail[j] for 0 j < m and 0 i < n. If no such pi exists, the state is unsafe � If alloc’[i, j] is 0 for all i and j, the state is safe � 4. Set alloc’[i, j] to 0; deallocate all resources held by pi; go to Step 2 62

Example Maximum Claim Process p 0 p 1 p 2 p 3 p 4 R 0 3 0 5 1 3 R 1 2 2 1 5 0 C = <8, 5, 9, 7> R 2 1 5 0 3 3 R 3 4 2 5 0 3 Allocated Resources Process p 0 p 1 p 2 p 3 p 4 Sum R 0 2 0 4 0 1 7 R 1 0 2 0 3 R 2 1 2 0 1 3 7 R 3 1 1 3 0 0 5 • Compute total allocated • Determine available units avail = <8 -7, 5 -3, 9 -7, 7 -5> = <1, 2, 2, 2> • Can anyone’s maxc be met? maxc[2, 0]-alloc’[2, 0] = 5 -4 = 1 1 = avail[0] maxc[2, 1]-alloc’[2, 1] = 1 -0 = 1 2 = avail[1] maxc[2, 2]-alloc’[2, 2] = 0 -0 = 0 2 = avail[2] maxc[2, 3]-alloc’[2, 3] = 5 -3 = 2 2 = avail[3] • P 2 can exercise max claim avail[0] = avail[0]+alloc’[2, 0] = 1+4 = 5 avail[1] = avail[1]+alloc’[2, 1] = 2+0 = 2 avail[2] = avail[2]+alloc’[2, 2] = 2+0 = 2 avail[3] = avail[3]+alloc’[2, 3] = 2+3 = 5 63

Example Maximum Claim Process p 0 p 1 p 2 p 3 p 4 R 0 3 0 5 1 3 R 1 2 2 1 5 0 C = <8, 5, 9, 7> R 2 1 5 0 3 3 R 3 4 2 5 0 3 Allocated Resources Process p 0 p 1 p 2 p 3 p 4 Sum R 0 2 0 0 0 1 3 R 1 0 2 0 3 R 2 1 2 0 1 3 7 R 3 1 1 0 0 0 2 • Compute total allocated • Determine available units avail = <8 -7, 5 -3, 9 -7, 7 -5> = <5, 2, 2, 5> • Can anyone’s maxc be met? maxc[4, 0]-alloc’[4, 0] = 5 -1 = 4 5 = avail[0] maxc[4, 1]-alloc’[4, 1] = 0 -0 = 0 2 = avail[1] maxc[4, 2]-alloc’[4, 2] = 3 -3 = 0 2 = avail[2] maxc[4, 3]-alloc’[4, 3] = 3 -0 = 3 5 = avail[3] • P 4 can exercise max claim avail[0] = avail[0]+alloc’[4, 0] = 5+1 = 6 avail[1] = avail[1]+alloc’[4, 1] = 2+0 = 2 avail[2] = avail[2]+alloc’[4, 2] = 2+3 = 5 avail[3] = avail[3]+alloc’[4, 3] = 5+0 = 5 64

Example Maximum Claim Process p 0 p 1 p 2 p 3 p 4 R 0 3 0 5 1 3 R 1 2 2 1 5 0 C = <8, 5, 9, 7> R 2 1 5 0 3 3 R 3 4 2 5 0 3 R 2 1 2 0 1 0 4 R 3 1 1 0 0 0 2 Allocated Resources Process p 0 p 1 p 2 p 3 p 4 Sum R 0 2 0 0 2 R 1 0 2 0 1 • Compute total allocated • Determine available units avail = <8 -7, 5 -3, 9 -7, 7 -5> = <6, 2, 5, 5> • Can anyone’s maxc be met? (Yes, any of them can) 65

Deadlock Detection and Recovery � � � Allow system to enter deadlock state Detection algorithm Recovery scheme 66

Detection & Recovery � � Check for deadlock (periodically or sporadically), then recover Can be far more aggressive with allocation No maximum claim, no safe/unsafe states Differentiate between � Serially reusable resources: A unit must be allocated before being released � Consumable resources: Never release acquired resources; resource count is number currently available 67

Deadlock Detection Algorithm � � � Available: A vector of length m indicates the number of available resources of each type. Allocation: An n x m matrix defines the number of resources of each type currently allocated to each process. Request: An n x m matrix indicates the current request of each process. If Request [ij] = k, then process Pi is requesting k more instances of resource type. Rj. 68

Detection Algorithm 1. Let Work and Finish be vectors of length m and n, respectively Initialize: (a) Work : = Available (b) For i = 1, 2, …, n, if Allocationi 0, then Finish[i] : = false; otherwise, Finish[i] : = true. 2. Find an index i such that both: (a) Finish[i] = false (b) Requesti Work If no such i exists, go to step 4. 3. (a) Work : = Work + Allocationi; (b) Finish[i] : = true; go to step 2. 4. If Finish[i] = false, for some i, 1 i n, then the system is in deadlock state. Moreover, if Finish[i] = false, then Pi is deadlocked. Algorithm requires an order of m x n 2 operations to detect whether the system is in deadlocked state. 69

Example of Detection Algorithm � Five processes P 0 through P 4; three resource types A (7 instances), B (2 instances), and C (6 instances). � Snapshot at time T 0: Allocation. Request Available ABC ABC P 0 0 1 0 000 P 1 2 0 0 202 P 2 3 000 P 3 2 1 1 100 P 4 0 0 2 002 � Sequence <P 0, P 2, P 3, P 1, P 4> will result in Finish[i] = true for all i. 70

Example - cont. � P 2 requests an additional instance of type C. Allocation Request P 0 P 1 P 2 P 3 P 4 � State ABC 010 200 303 211 002 Available ABC 000 202 001 100 002 of system? Can reclaim resources held by process P 0, but insufficient resources to fulfill other processes; requests. � Deadlock exists, consisting of processes P 1, P 2, P 3, and P 4. � 71

Reusable Resource Graphs (RRGs) � � Micro model to describe a single state A directed graph such that � n+m nodes represent n processes and m resources Nodes = {p 0, p 1, …, pn} {R 1, R 2, …, Rm} � Edges connect pi to Rj, or Rj to pi (pi, Rj) is a request edge for one unit of Rj (Rj, pi) is an assignment edge of one unit of Rj � For each Rj there is a count, cj of units Graphically represented by tokens inside Rj Rj � Number of units of Rj allocated to pi plus the number requested by pi cannot exceed cj 72
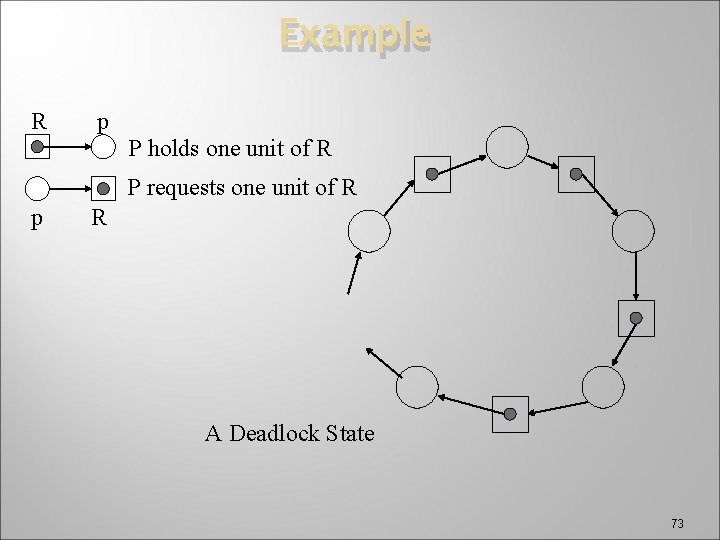
Example R p P holds one unit of R P requests one unit of R p R A Deadlock State 73
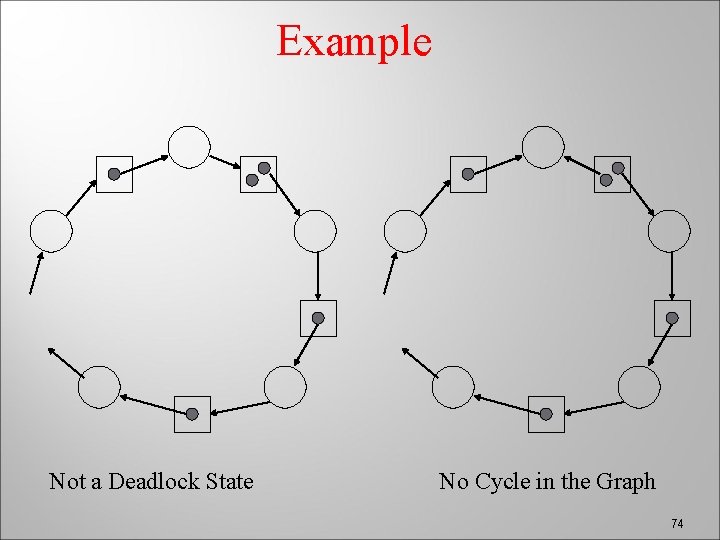
Example Not a Deadlock State No Cycle in the Graph 74

State Transitions due to Request � � In Sj, pi is allowed to request q ch units of Rh, provided pi has no outstanding requests. Sj Sk, where the RRG for Sk is derived from Sj by adding q request edges from pi to Rh q edges pi Rh State Sj pi request q units of Rh pi Rh State Sk 75

State Transition for Acquire � � In Sj, pi is allowed to acquire units of Rh, iff there is (pi, Rh) in the graph, and all can be satisfied. Sj Sk, where the RRG for Sk is derived from Sj by changing each request edge to an assignment edge. pi Rh State Sj pi acquires units of Rh pi Rh State Sk 76

State Transition for Release � � In Sj, pi is allowed to release units of Rh, iff there is (Rh, pi) in the graph, and there is no request edge from pi. Sj Sk, where the RRG for Sk is derived from Sj by deleting all assignment edges. pi Rh State Sj pi releases units of Rh pi Rh State Sk 77
Example p 0 p 1 S 00 78
Example p 0 p 1 S 00 S 01 79
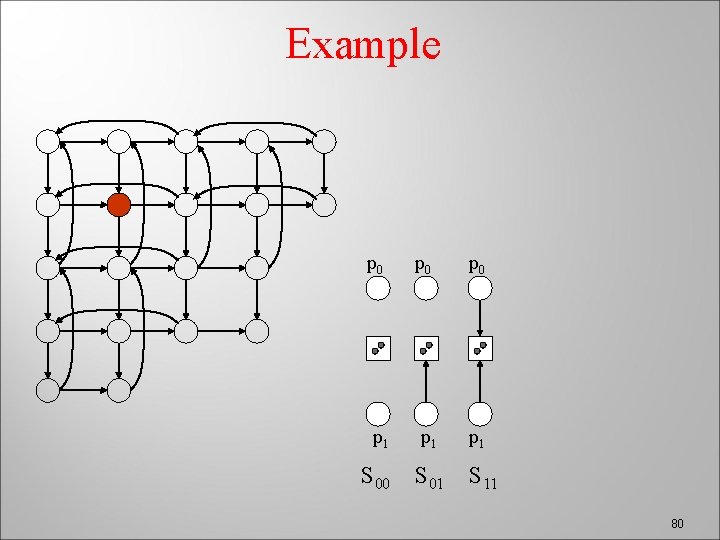
Example p 0 p 0 p 1 p 1 S 00 S 01 S 11 80
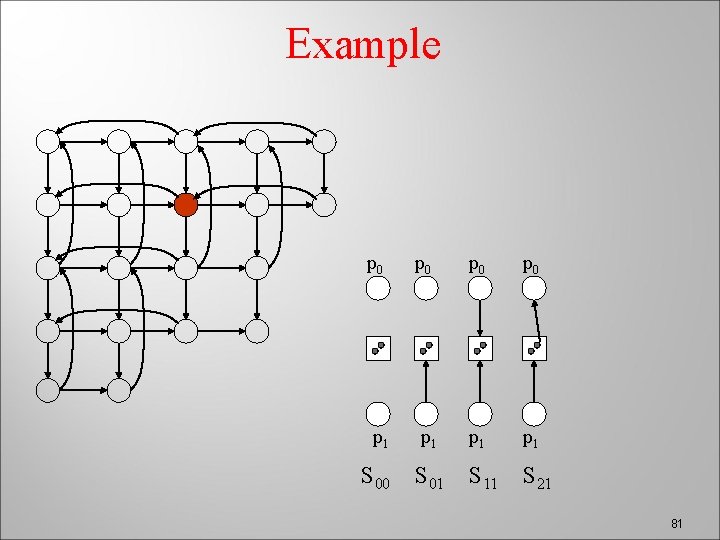
Example p 0 p 0 p 1 p 1 S 00 S 01 S 11 S 21 81
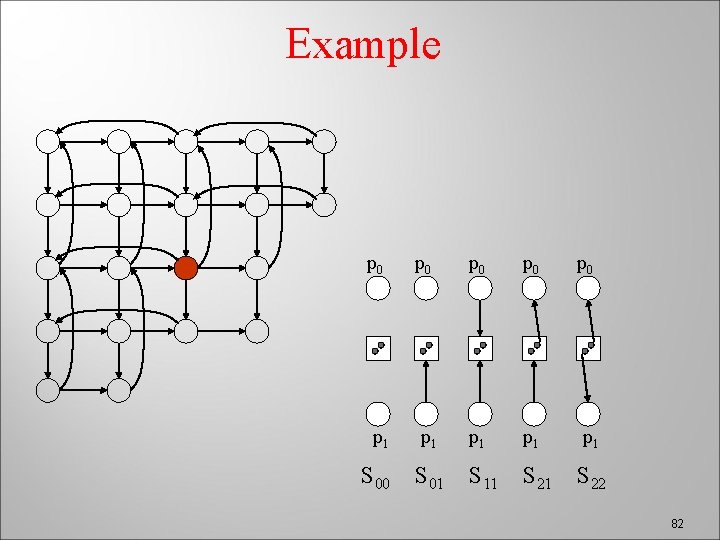
Example p 0 p 0 p 0 p 1 p 1 p 1 S 00 S 01 S 11 S 22 82
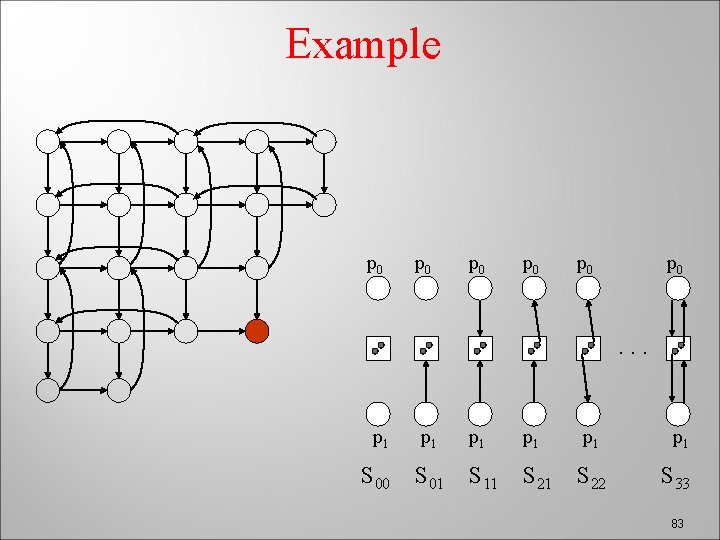
Example p 0 p 0 p 0 . . . p 1 p 1 p 1 S 00 S 01 S 11 S 22 S 33 83

Graph Reduction � � � Deadlock state if there is no sequence of transitions unblocking every process A RRG represents a state; can analyze the RRG to determine if there is a sequence A graph reduction represents the (optimal) action of an unblocked process. Can reduce by pi if � pi is not blocked � pi has no request edges, and there are (Rj, pi) in the RRG 84

Graph Reduction (cont) � � Transforms RRG to another RRG with all assignment edges into pi removed Represents pi releasing the resources it holds pi Reducing by pi pi 85

Graph Reduction (cont) � � A RRG is completely reducible if there a sequence of reductions that leads to a RRG with no edges A state is a deadlock state if and only if the RRG is not completely reducible. 86
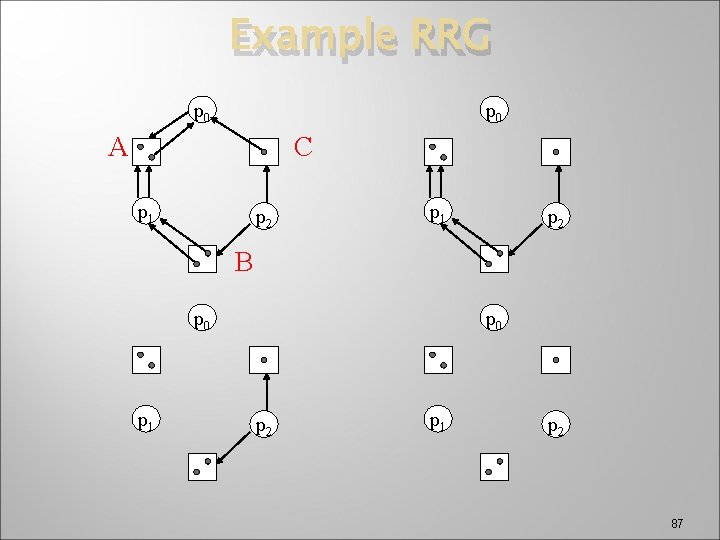
Example RRG p 0 A C p 1 p 2 B p 0 p 1 p 0 p 2 p 1 p 2 87

Corresponding Detection Algorithm �Three processes P 0 through P 2; three resource types A (2 instances), B (2 instances), and C (1 instance). �Snapshot at time T 0: Allocation Request Available ABC P 0 1 1 0 0 P 1 0 2 0 0 P 2 0 0 1 1 ABC 100 88
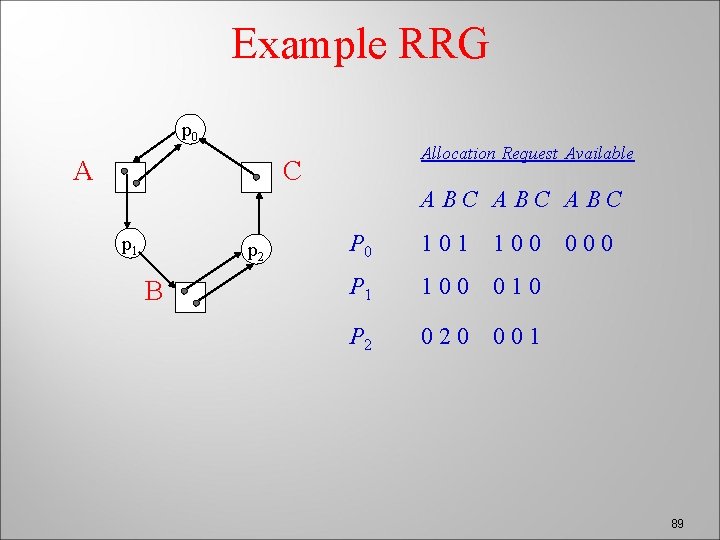
Example RRG p 0 A Allocation Request Available C p 1 p 2 B ABC ABC P 0 101 100 P 1 100 010 P 2 020 001 000 89

Consumable Resource Graphs (CRGs) � � � Number of units varies, have producers/consumers Nodes = {p 0, p 1, …, pn} {R 1, R 2, …, Rm} Edges connect pi to Rj, or Rj to pi � (pi, Rj) is a request edge for one unit of Rj � (Rj, pi) is an producer edge (must have at least one producer for each Rj) � For each Rj there is a count, wj of units Rj 90

State Transitions due to Request • In Sj, pi is allowed to request any number of units of Rh, provided pi has no outstanding requests. • Sj Sk, where the RRG for Sk is derived from Sj by adding q request edges from pi to Rh q edges pi Rh State Sj pi request q units of Rh pi Rh State Sk 91

State Transition for Acquire • In Sj, pi is allowed to acquire units of Rh, iff there is (pi, Rh) in the graph, and all can be satisfied. • Sj Sk, where the RRG for Sk is derived from Sj by deleting each request edge and decrementing wh. pi Rh State Sj pi acquires units of Rh pi Rh State Sk 92

State Transition for Release • In Sj, pi is allowed to release units of Rh, iff there is (Rh, pi) in the graph, and there is no request edge from pi. • Sj Sk, where the RRG for Sk is derived from Sj by incrementing wh. pi Rh State Sj pi releases 2 units of Rh pi Rh State Sk 93
Example p 0 p 0 p 0 p 1 p 1 p 1 94

Deadlock Detection � � May have a CRG that is not completely reducible, but it is not a deadlock state For each process: � Find at least one sequence which leaves each process unblocked. � There may be different sequences for different processes -- not necessarily an efficient approach 95

Deadlock Detection • May have a CRG that is not completely reducible, but it is not a deadlock state • Only need to find sequences, which leave each process unblocked. p 0 p 1 96

Deadlock Detection • May have a CRG that is not completely reducible, but it is not a deadlock state • Only need to find a set of sequences, which leaves each process unblocked. 97

General Resource Graphs � � � Have consumable and reusable resources Apply consumable reductions to consumables, and reusable reductions to reusables See Figure 10. 30 98
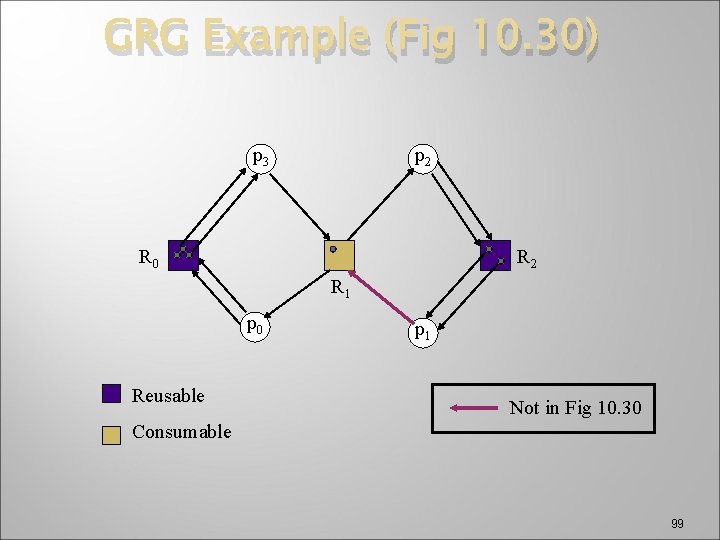
GRG Example (Fig 10. 30) p 3 p 2 R 0 R 2 R 1 p 0 Reusable p 1 Not in Fig 10. 30 Consumable 99
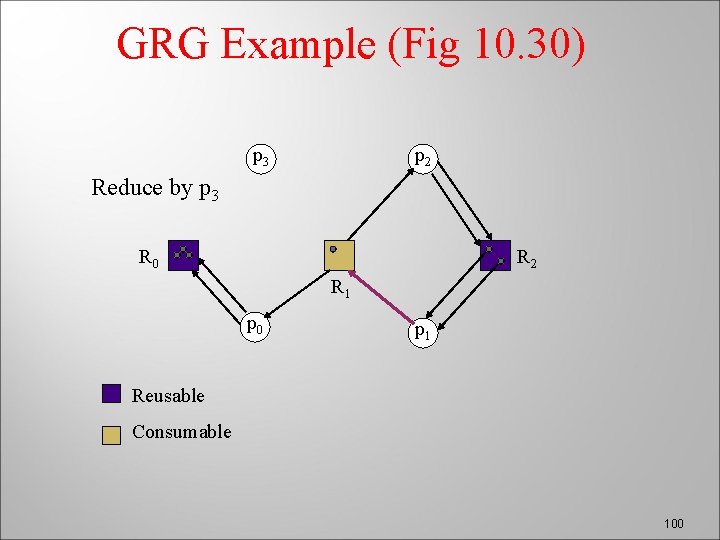
GRG Example (Fig 10. 30) p 3 p 2 Reduce by p 3 R 0 R 2 R 1 p 0 p 1 Reusable Consumable 100
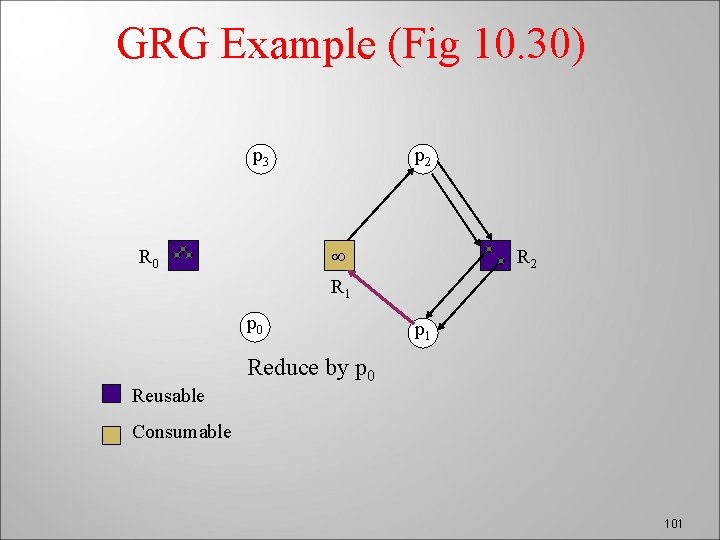
GRG Example (Fig 10. 30) p 3 p 2 R 1 R 0 p 0 R 2 p 1 Reduce by p 0 Reusable Consumable 101

Detection-Algorithm Usage � When, and how often, to invoke depends on: � How often a deadlock is likely to occur? � How many processes will need to be rolled back? one for each disjoint cycle � If detection algorithm is invoked arbitrarily, there may be many cycles in the resource graph and so we would not be able to tell which of the many deadlocked processes “caused” the deadlock. 102

Recovery � No magic here � Choose a blocked process � Preempt it (releasing its resources) � Run the detection algorithm � Iterate if until the state is not a deadlock state 103

Recovery from Deadlock: Process Termination � � � Abort all deadlocked processes. Abort one process at a time until the deadlock cycle is eliminated. In which order should we choose to abort? � Priority of the process. � How long process has computed, and how much longer to completion. � Resources the process has used. � Resources process needs to complete. � How many processes will need to be terminated. � Is process interactive or batch? 104

Recovery from Deadlock: Resource Preemption � � � Selecting a victim – minimize cost. Rollback – return to some safe state, restart process from that state. Starvation – same process may always be picked as victim, include number of rollback in cost factor. 105

Combined Approach to Deadlock Handling � Combine three basic approaches � prevention � avoidance � detection � � � Allowing the use of the optimal approach for each of resources in the system. Partition resources into hierarchically ordered classes. Use most appropriate technique for handling deadlocks within each class. 106
- Slides: 106