DEA Perception et Traitement de lInformation Reconnaissance des











- Slides: 22

DEA Perception et Traitement de l’Information Reconnaissance des formes discrimination linéaire S. Canu http: //psichaud. insa-rouen. fr/~scanu/Rd. F

Buts de la Rd. F Une forme x (vecteur forme des caractéristiques) D : Algorithme de Reconnaissance des Formes C’est la forme « y=D(x) » Nous voulons un algorithme de Rd. F performant

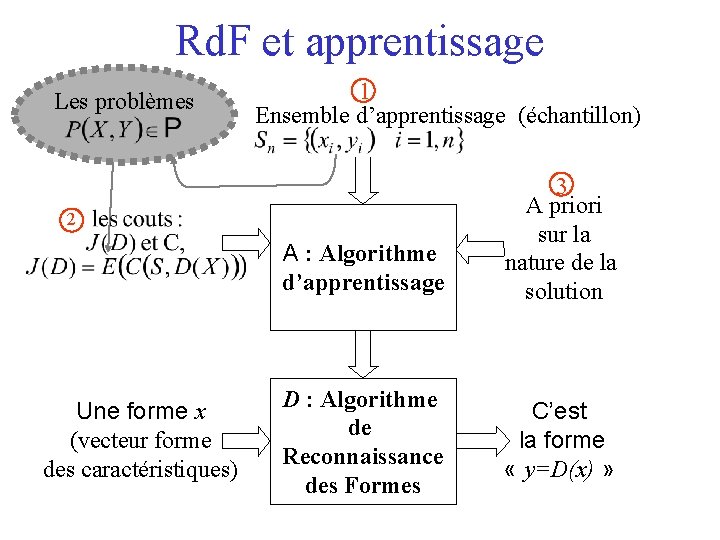
Rd. F et apprentissage Les problèmes 1 Ensemble d’apprentissage (échantillon) 2 A : Algorithme d’apprentissage Une forme x (vecteur forme des caractéristiques) D : Algorithme de Reconnaissance des Formes 3 A priori sur la nature de la solution C’est la forme « y=D(x) »

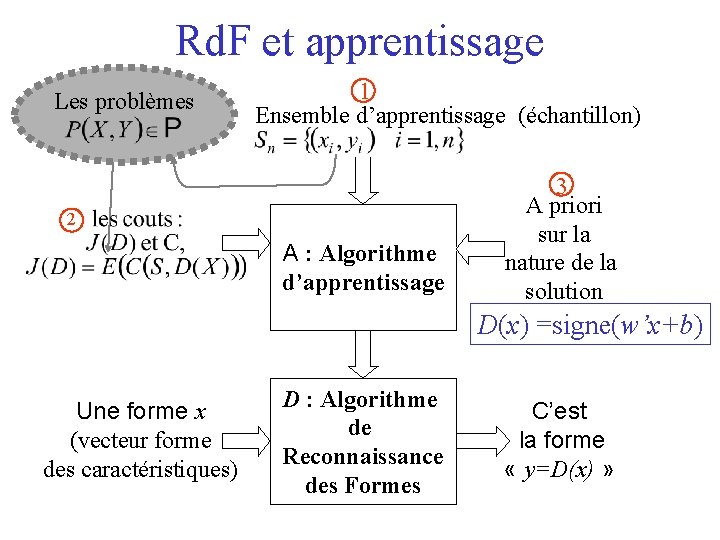
Rd. F et apprentissage Les problèmes 1 Ensemble d’apprentissage (échantillon) 2 A : Algorithme d’apprentissage 3 A priori sur la nature de la solution D(x) =signe(w’x+b) Une forme x (vecteur forme des caractéristiques) D : Algorithme de Reconnaissance des Formes C’est la forme « y=D(x) »

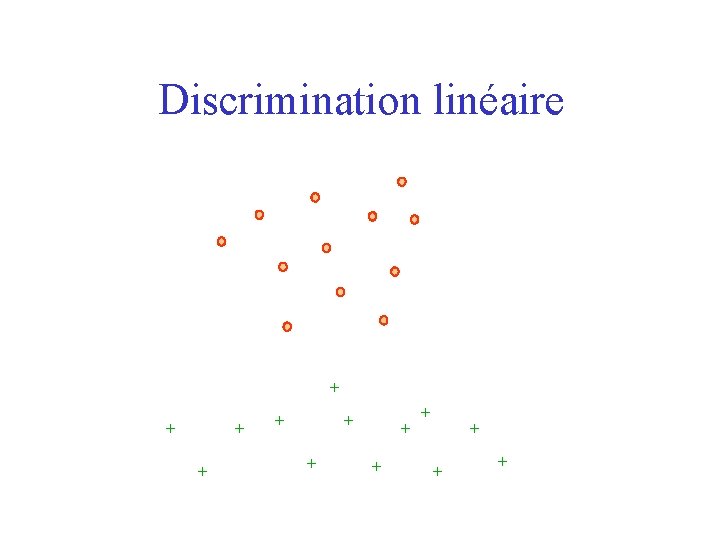
Discrimination linéaire + + + +

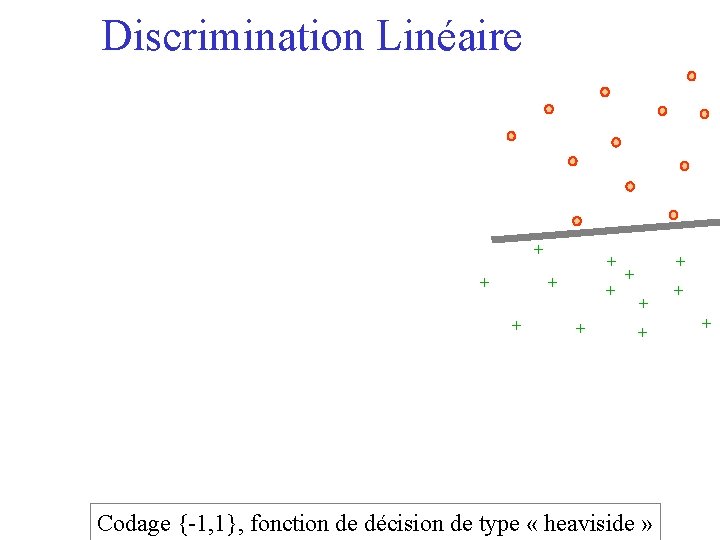
Discrimination Linéaire + + + Codage {-1, 1}, fonction de décision de type « heaviside » + +

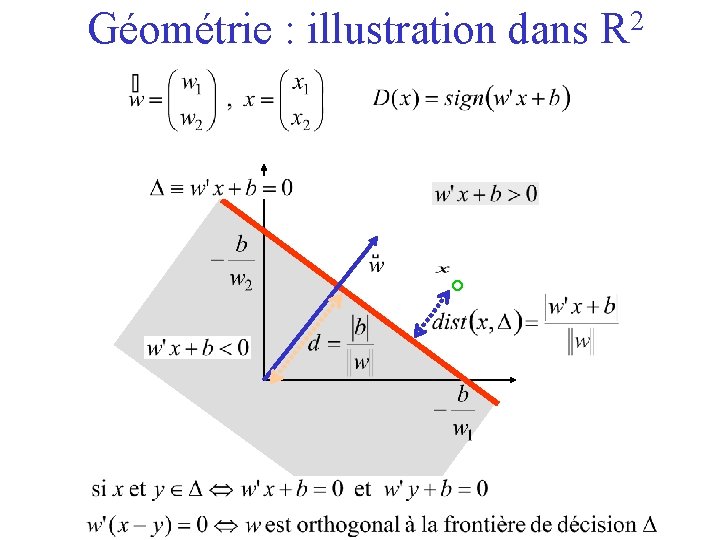
Codage et géomètrie w’x : produit scalaire

Géométrie : illustration dans R 2 °

Quand le discriminateur linéaire est il optimal ? • Quand on le sait à priori… • quand les 2 classes sont gaussiènnes (même matrice de variance covariance, couts 0 -1) • quand on a peu d’exemples par rapport à d (rapport n/d). . . et que l’on n’a pas de modèle on peut l’utiliser pour « représenter » les données (cf ACP) Avantages : il est simple on connaît des bornes de l’erreur

MAP : cas gaussien

Cas gaussien 1 d Règle de décision Exemple : communication binaire synchrone la source 1 émet des 0 et la source 2 des 1, le canal est bruité par un bruit blanc, on observe

Erreur de décision

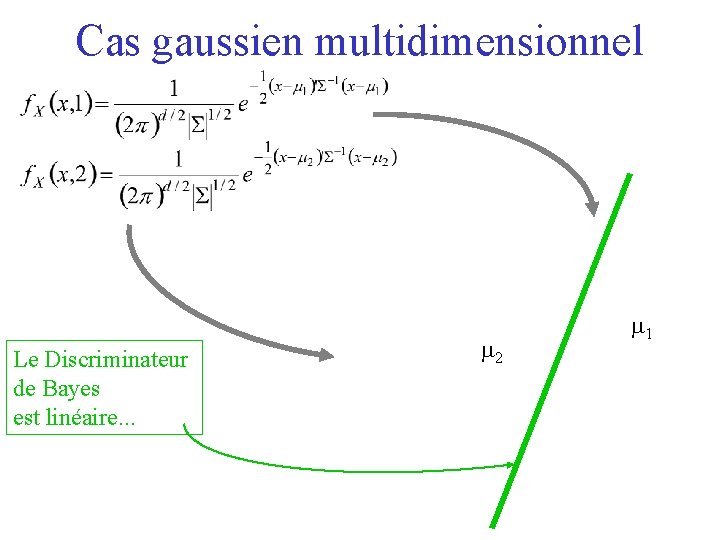
Cas gaussien multidimensionnel Le Discriminateur de Bayes est linéaire. . . m 2 m 1

Cas Gaussien (même variance) . . .

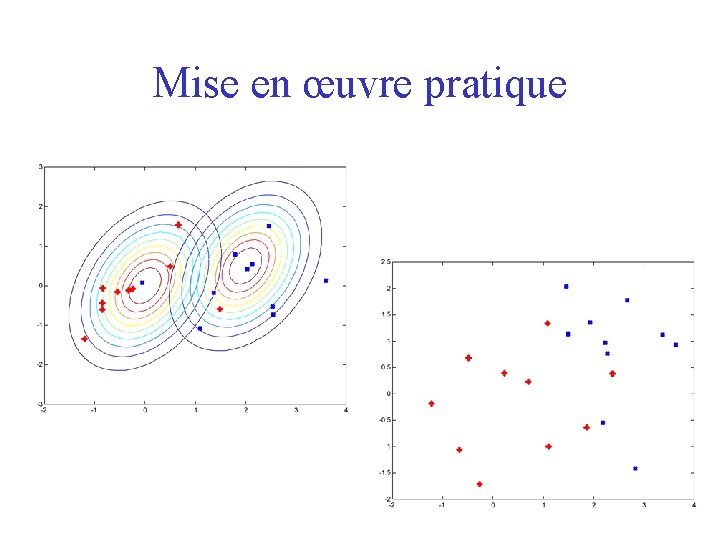
Mise en œuvre pratique

Estimation. . . et rêve

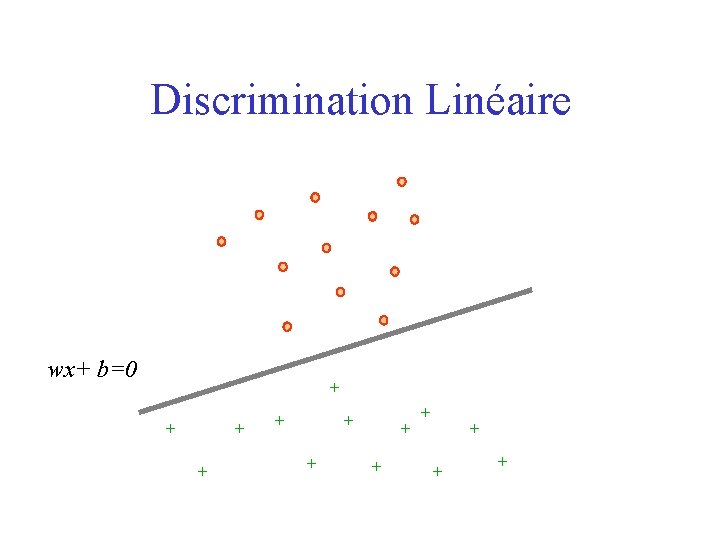
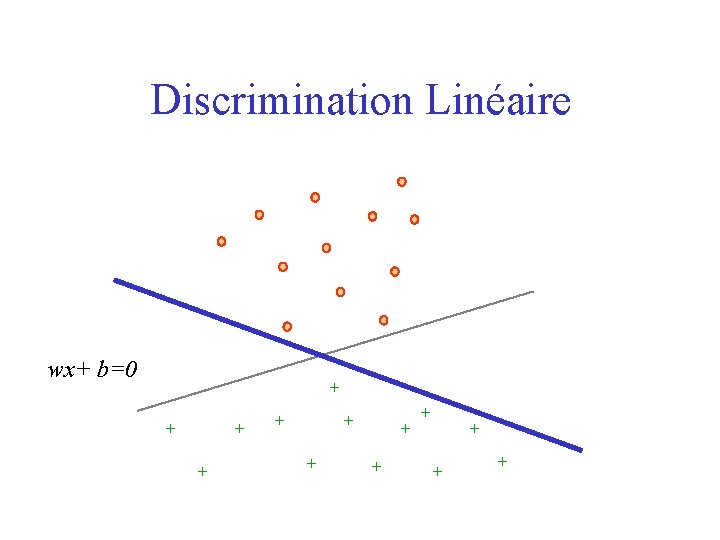
Discrimination Linéaire wx+ b=0 + + + +

Discrimination Linéaire wx+ b=0 + + + +

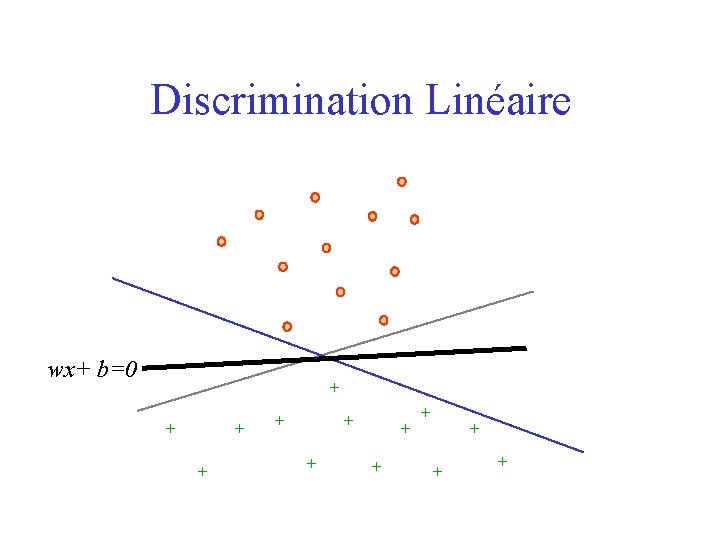
Discrimination Linéaire wx+ b=0 + + + +

Discrimination Linéaire wx+ b=0 + + + +

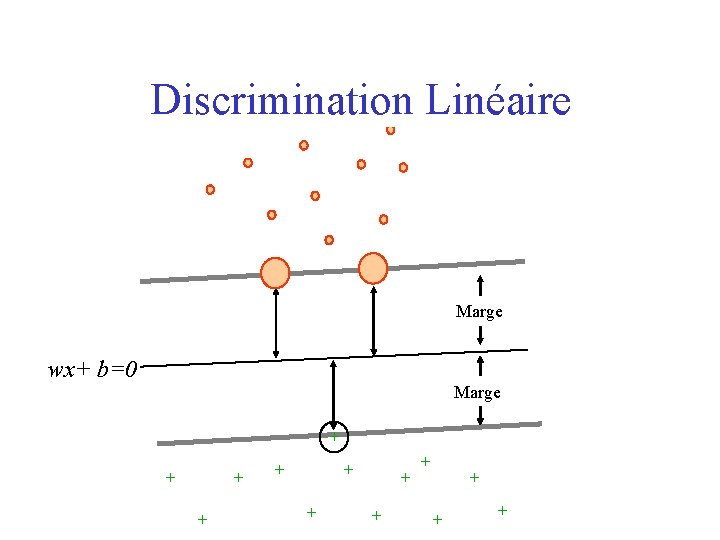
Discrimination Linéaire Marge wx+ b=0 Marge + + + +

Marge d’un classifieur Définition • frontière • marge • point influent : « proche » de la frontière, • point influent pour une règle D : si l’étiquette change, la frontière change « significativement » (un des points • point non influent