De Morgans Laws A B A B A

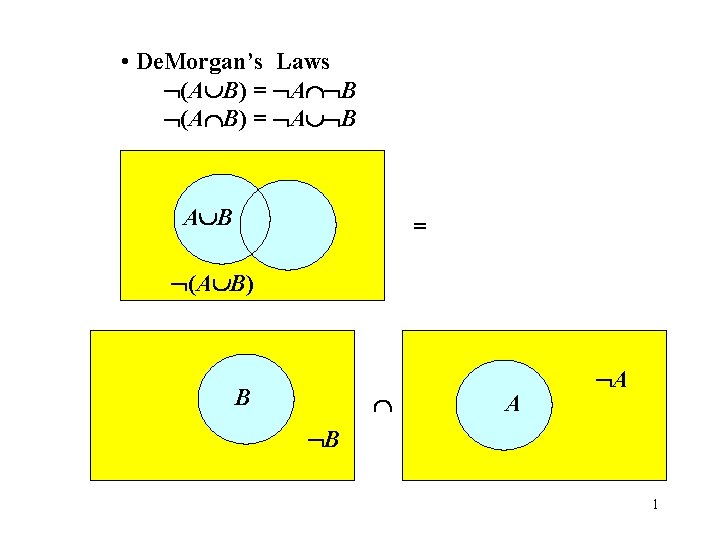
• De. Morgan’s Laws (A B) = A B A B = (A B) B A A B 1

Example of using De. Morgan’s Law Let A = {a, d, e, g} and B = {c, d, f, g} from the universe U = {a, b, c, d, e, f, g, h, i}. To verify that (A B) = A B find each of these two sets independently to find that they are indeed the same. 1) (A B)= {a, c, d, e, f, g} = {b, h, i} 2) A B= {b, c, f, h, i} {a, b, e, h, i} ={b, h, i} are the same, as predicted. 2

• Domination Laws A U = U A = • Absorption Laws A (A B) =A A (A B) = A p T T p F F p (p q) p p (p q) p These laws can be proved by using logic laws or membership tables. 3

What is a proof? A proof is a method of ascertaining truth. In everyday life different kinds of proofs are acceptable: • Jury trial. • Word of God. • Word of Boss. • Experimental science: The truth is guesses and confirmed or refuted by experiments. • Sampling: like public opinion is obtained by polling. • Inner conviction. . These are not valid proofs in mathematical sense. They all can go wrong… 4

Mathematics uses a particularly convincing way to argue that something is true. Definition. A proof is a formal verification of a proposition by a chain of logical deductions starting from the base set of axioms. A proof takes axioms and definitions and uses deduction rules, step by step, to get a desired conclusion. 5

Proof methods · If a statement considers a few numbers of cases it can be proved by exhaustive checking. Example: All students in this class are computer science major. We can easily verify is it true or false. · Truth table method. To prove a statement about small number Boolean variables make a truth table and check all possible cases. Example: (p q) ( q p). By inspection we see that lhs has the same truth value as the rhs for all values of p and q. 6

Theorem 1. Let A and B be any two sets. Prove that A A B • How can we prove that A A B for any sets A and B? It is not sufficient to consider 10 or 100 (or even 1000, etc. ) different sets! We must prove it in general. • First we need to use the definition of subset relation to state what we need to prove in the formal way: A A B x [x A B]. • To prove something for any x, it is sufficient to prove it for arbitrary x. So, take arbitrary x and prove that if x A, then x A B. 7

Proof. Assume x is arbitrary element from set A x A, (1). But x A (any other proposition) by the inference rule p p q ( or since p p q is a tautology) So, (1) implies in particular, that x A x B, (2). By the definition of set union, (2) is equivalent to x A B, (3). We showed that arbitrary element x from set A belongs to the union A B, that is A A B. 8

Now you might be able to prove in similar way the following Theorem 2. Let A and B be any two sets. Prove that A B A. Proof. We need to prove that for any x such that x A B, x A, i. e. x [x A B x A]. So, take arbitrary x A B (1). By the definition of the set intersection (1) implies that x A x B, (2) implies that x A, (3) by the inference rule p q p. We showed that any element from A B belongs to A. By the definition of subset relation it means that A B A. 9

Theorem 3. Let A, B and C be any sets. Then if A B and B C , then A C. p q • To prove a statement p q means to show that it is always true, or it is a tautology. • If p is false, the whole implication is true regardless of the value of q. So, if p is false we have nothing to prove. • If p is true, than the whole implication may turn to false if q is false. We need to show that it never happens. In other words, we need to show that if p is true than q is always true. 10

This is called a direct proof. In direct proof we assume that p is true. Making use of this assumption and any other relevant facts (definitions, axioms, principles, proved theorems, etc. ) we build a chain of logical reasoning leading to the conclusion that q is true. Proof. Assume p: A B and B C to prove q: A C. To prove A C take any x A, (1) to show that x C. By assumption A B and subset definition, it can be implied from (1) that x B, (2). By assumption B C it can be implied from (2) that x C, (3). We showed that any element from A belongs to C, that is A C. So, assuming p we showed that q is implied, or p q is always true. 11

We can prove some more theorems by using definitions, logical reasoning and other theorems. Theorem 4. Let A and B be any sets. Then A B if and only if each of the following holds: a) A B=B. A B=B B A B 1. A B=B A B B (by Theorem 1) x A B x B 2. A B=B A B x B 12

Proof. 1). Assume A B. To prove A B=B we need to prove B A B and A B B. B A B by the Theorem 1. To prove A B B take some x A B. By assumption A B, x A B implies that x B B, but B B=B by idempotent property, so x B. So, we showed that for arbitrary x, x A B x B, i. e. A B B. 2). Assume A B=B. To prove A B take any x A. By the Theorem 1, x A implies x A B. By assumption A B=B, x A B implies x B. So, for arbitrary x A x B, i. e. A B. We proved A B=B and A B=B A B. So, it implies that A B=B 13

b) A B=A. A B 1. A B=A A B A A A B (by Theorem 2) x A x B x A B 2. A B =A A B x A B x B 14

Proof. 1). Assume A B. We need to prove A B A and A A B A by the Theorem 2. To prove A A B take an arbitrary x A. By assumption A B, x A implies that x B, so now we have x A and x B, i. e. x A B by the definition of A B. 2). Assume A B=A. To prove A B take some x A. By assumption A B=A, x A implies x A B. By the Theorem 2, x A B implies x B. We proved implications in both directions, A B=A and A B =A A B , that means the propositions are equivalent, A B =A A B 15

c) A B= If you can build the chain of identical (in both directions) transformations, then you don’t need double inclusion. A B x [x A x B] x [x A B] x [x A B] A B = by subset definition by equivalence p q by De. Morgan’s law by definition of A B by negation of by definition of empty set 16

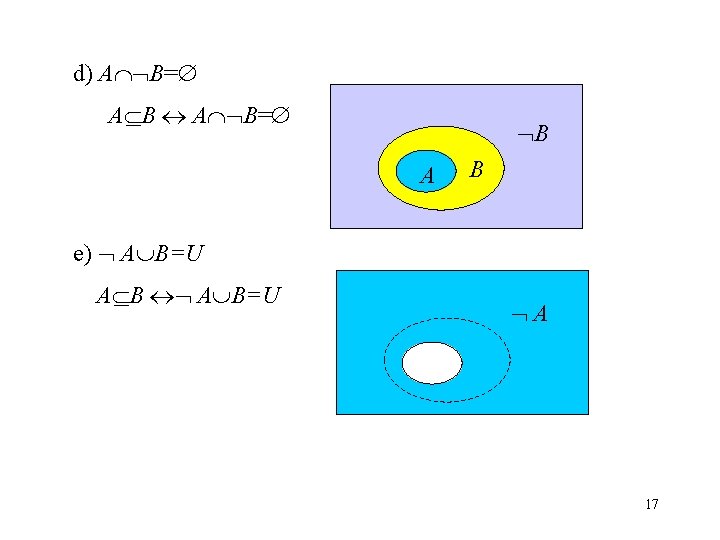
d) A B= A B= B A B e) A B=U A B=U A 17

f) B A A B B A x [x B x A] x [x A x B] A B by definition of set compliment by equivalence of an implication and its contrapositive. 18

U B A 19

Theorem 5. Let A, B and C be arbitrary sets. Prove that if A B = C B and A B = C B, then A = C. Direct proof of p q Assume p: A B = C B and A B = C B to prove q: A = C The equality of two sets can be proved as two subset relations (‘double inclusion’ ): A C C A A=C So, there should be two parts of the proof. 1). A B = C B and A B = C B A C x A x A B x C B x A B x C 2). A B = C B and A B = C B C A 20

Part 1: proof of A C Assume A B = C B (1) and A B = C B (2). To prove A C we need to show that any element from A belongs to C, x [x A x C]. So, take arbitrary element x A (3) to show that x C. By the Theorem 1, (3) implies x A B (4). By assumption (1) we conclude from (4) that x C B (5), or by the definition of the set union that x C or x B (6). So, we have one of two cases to consider. Case x C: we are done. Case x B: we can imply x A B (7) by the Theorem 2. By assumption (2) it can be implied from (7) that x C B (8). From (8) we can conclude that x C making use of the Theorem 2. So, in both cases we come to x C. QED. 21