De Bruijn sequences Novembers 2005 Rotating drum problem

De Bruijn sequences 陳柏澍 Novembers 2005

Rotating drum problem n n Each of the segments is one of two types, denoted by 0 and 1. Any four consecutive segments uniquely determine the position of the drum. 0000 0001 0011

Rotating drum problem n The problem above means that the 16 possible quadruples of consecutive 0’s and 1’s on the drum should be the binary representations of the integers 0 to 15(in other words, all distinct).

Rotating drum problem n n The first, can this be done? The second, if yes, in how many different ways?

Rotating drum problem n Both questions were treated by N. G. de Bruijn(1946)and for this reason the graphs described later and the corresponding circular sequence are often called De Bruijn graphs and De Bruijn sequences, respectively.

Rotating drum problem n n Consider a diagraph by taking all 3 -bit binary words as vertices and joining the vertex by a directed edge to and. The arc is labeled.
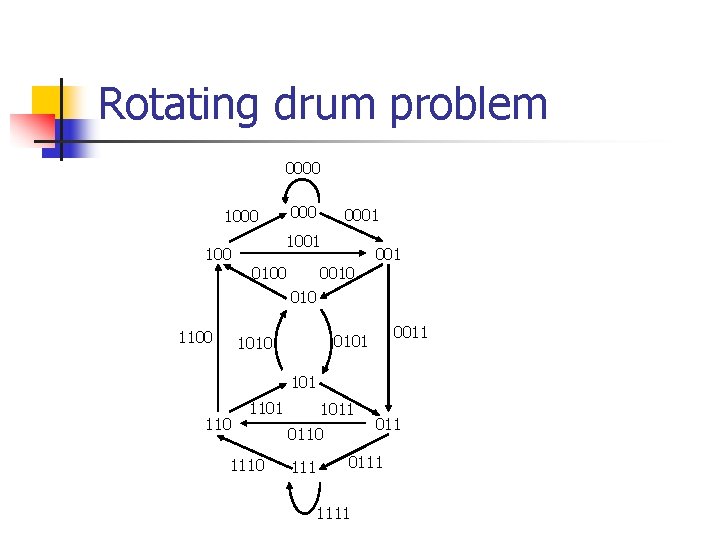
Rotating drum problem 0000 1000 100 0001 1001 0100 001 010 1100 0011 0101 1010 101 1101 1110 1011 0110 111 0111 1111

Rotating drum problem n n n Clearly, the graph is strong connected and every vertex has in-degree 2 and out-degree 2. So the graph is Eulerian. The Eulerian circuit with specified edge label forms the circular arrangement we desired.
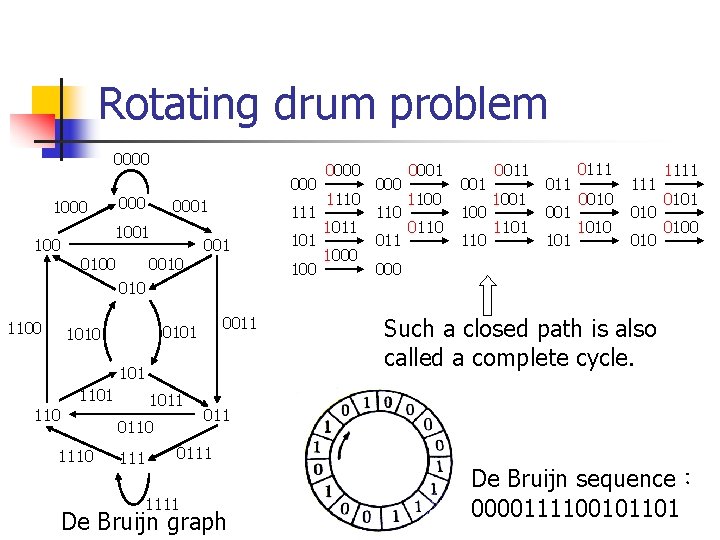
Rotating drum problem 0000 1000 100 0001 1001 0100 0010 111 001 100 0000 1110 1011 1000 110 011 0001 1100 0110 001 100 110 0011 1001 1101 011 001 101 0111 0010 1111 0100 000 010 1100 0011 0101 1010 101 110 1011 0110 111 Such a closed path is also called a complete cycle. 0111 1111 De Bruijn graph De Bruijn sequence: 0000111100101101

De Bruijn sequence n n A cyclic sequence is called De Bruijn sequence if following two properties are satisfied: (1) (2) distinct n-dim vectors Example:

De Bruijn graph n De Bruijn graph is a weighted diagraph that satisfies following two properties: (1) (2)Connecting to with the directed edge having the weight

De Bruijn graph n n Lemma 1: is Eulerian. Proof: Clearly, is strong connected and. Thus, it’s Eulerian. Lemma 2:All weights in Proof: Trivial from the definition. are all distinct.

De Bruijn sequence n Theorem 1: De Bruijn sequence exists. Proof: By Lemma 1, there exists a Eulerian circuit C in. Suppose C passes through edges. Suppose the weight of each edge is.

De Bruijn sequence Let , thus is the desired De Bruijn sequence. It can be easily check that any n consecutive segments of the sequence above maps to the weight of the unique edge. By Lemma 2, they are all distinct.

Doubled graph of De Bruijn graph n Let De Bruijn graph. Define the doubled graph of as follows: (1)each edge of corresponds to a vertex of.

Doubled graph of De Bruijn graph
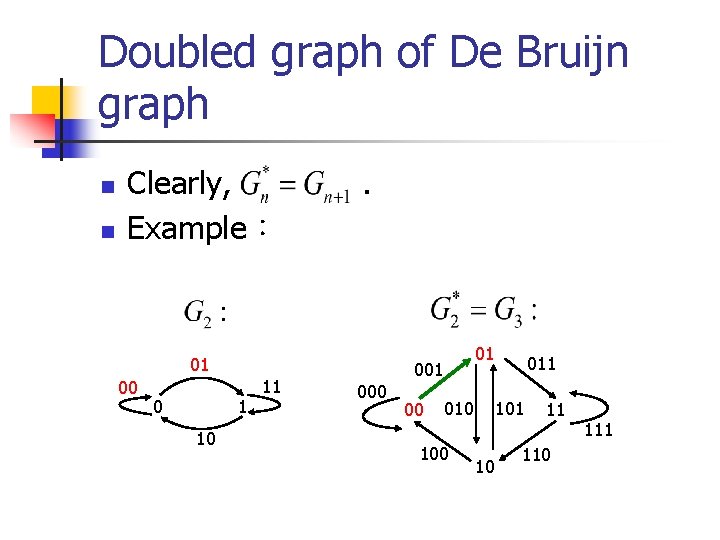
Doubled graph of De Bruijn graph n n Clearly, Example: 01 00 0 1 10 11 . 01 000 00 010 100 011 10 11 110 111

2 -in 2 -out graph n n 2 -in 2 -out graph is the diagraph with indegree 2 and out-degree 2 for very vertex. Clearly, and are both 2 -in 2 -out graph.

How many different ways n Theorem 2:Let be a 2 -in 2 -out graph on vertices with complete cycles. Then has complete cycles.
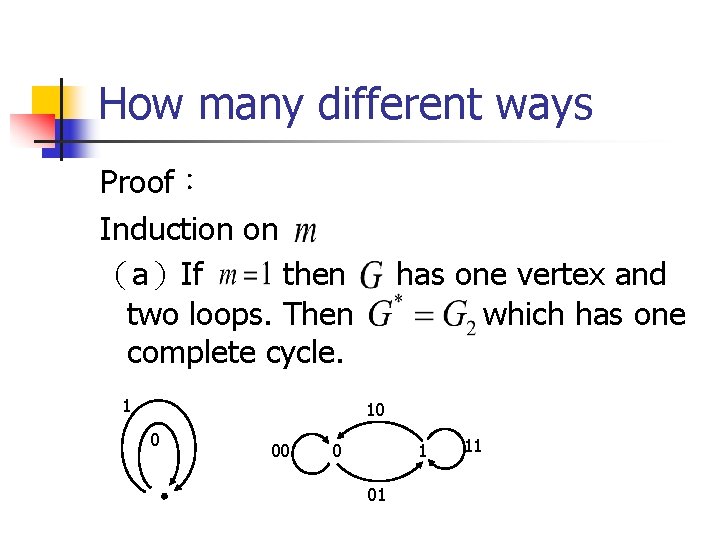
How many different ways Proof: Induction on (a)If then two loops. Then complete cycle. 1 has one vertex and which has one 10 0 00 0 1 01 11

How many different ways
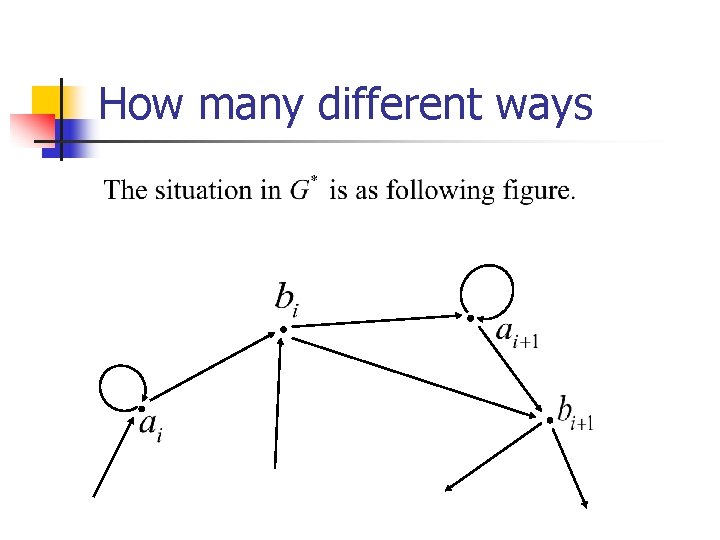
How many different ways

How many different ways
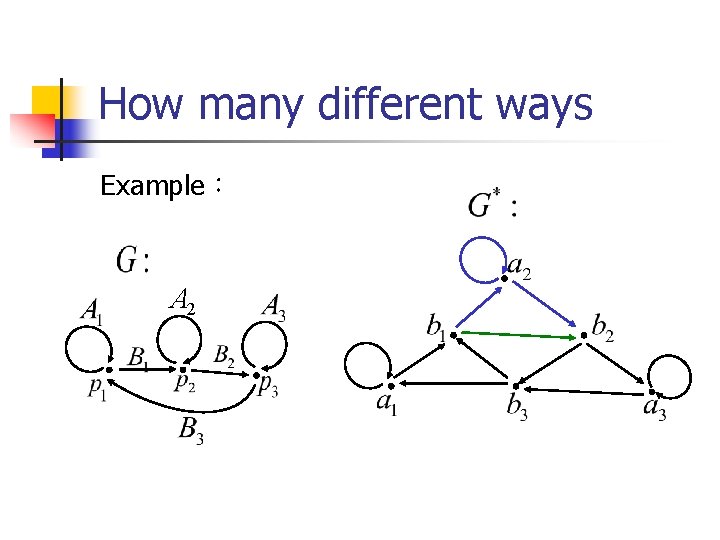
How many different ways Example: A 2

How many different ways
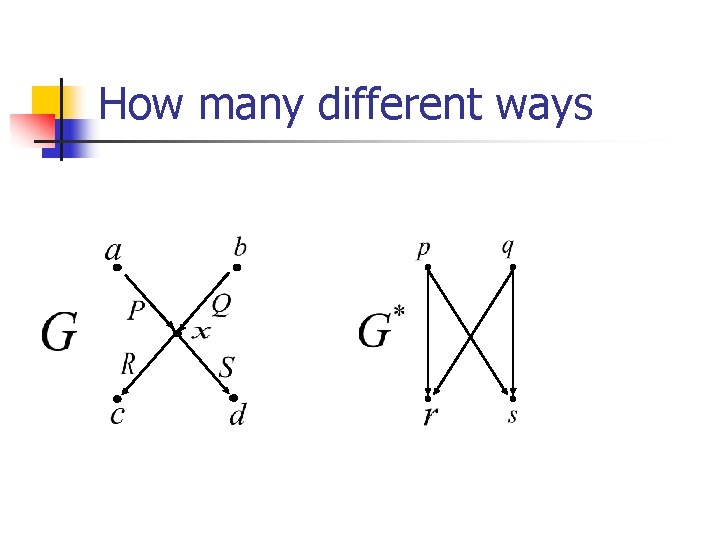
How many different ways

How many different ways

How many different ways
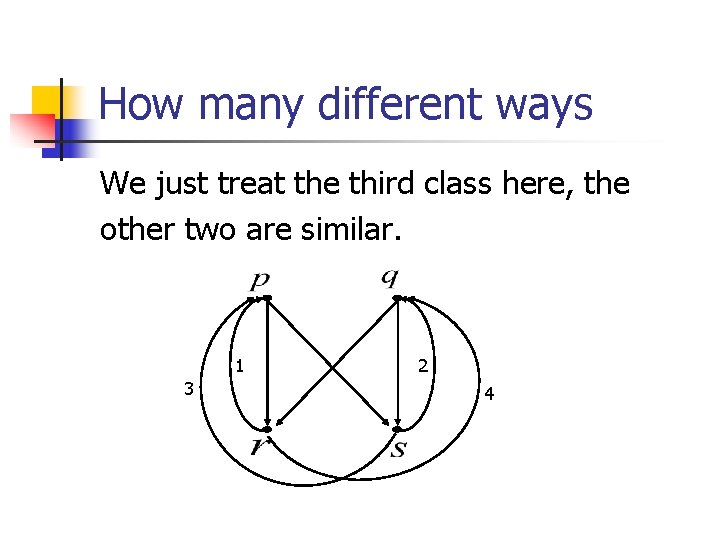
How many different ways We just treat the third class here, the other two are similar. 1 3 2 4
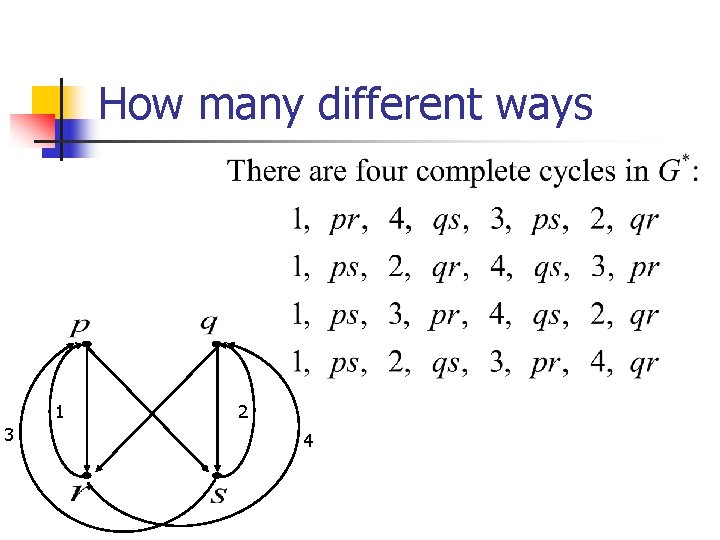
How many different ways 1 3 2 4
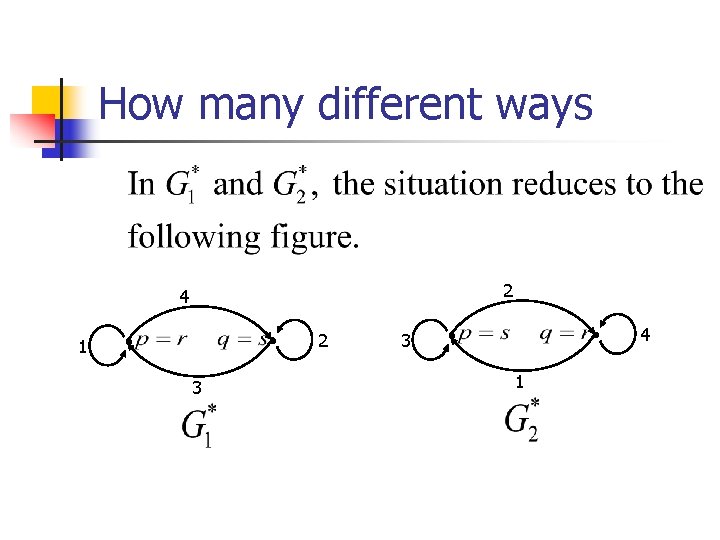
How many different ways 2 4 2 1 3 4 3 1

How many different ways

How many different ways

How many different ways

How many different ways

How many different ways
- Slides: 36