DDPIn Distance and Density Based Protein Indexing David

DDPIn Distance and Density Based Protein Indexing David Hoksza Charles University in Prague Department of Software Engineering Czech Republic CIBCB 2009

Presentation Outline n Biological background n Similarity search in protein structure databases n DDPIn ¡ ¡ ¡ feature vector extraction metrics querying n n one-step approach multi-step approach n Experimental results n Conclusion CIBCB 2009 2

Biological Background n Proteins ¡ ¡ molecules translated from m. RNA in ribosomes n ¡ ¡ n sequence of amino acids (20 AAs) coded by codon (triplet of nucleotides) Function of a protein derived from its three dimensional structure ¡ ¡ n DNA → RNA → protein → similar proteins have similar functions similar proteins have a common ancestor Identifying protein structure → finding similar proteins → getting clue to the function CIBCB 2009 3

Similarity Search in Protein Databases n Similarity between a pair of proteins ¡ alignment + similarity score n n ¡ n RMSD, TM-score, … visual inspection DALI, CE, SAP, VAST… Classification ¡ SCOP (Structural Classification of Proteins) ¡ ¡ no need for an alignment indexing various features ¡ PSI, PSIST, Pro. Gre. SS, CTSS, …DDPIn CIBCB 2009 4

DDPIn - Overview n Distance and Density based Protein Indexing n Classification method Indexing of protein features n ¡ ¡ distances among Cα atoms used each AA represents a feature → protein p consists of |p| features n various semantics used ¡ ¡ metric indexing employed (M-tree) n ¡ based on clustering Cα atoms into rings k. NN querying outcomes of several searches are merged to obtain final results CIBCB 2009 5

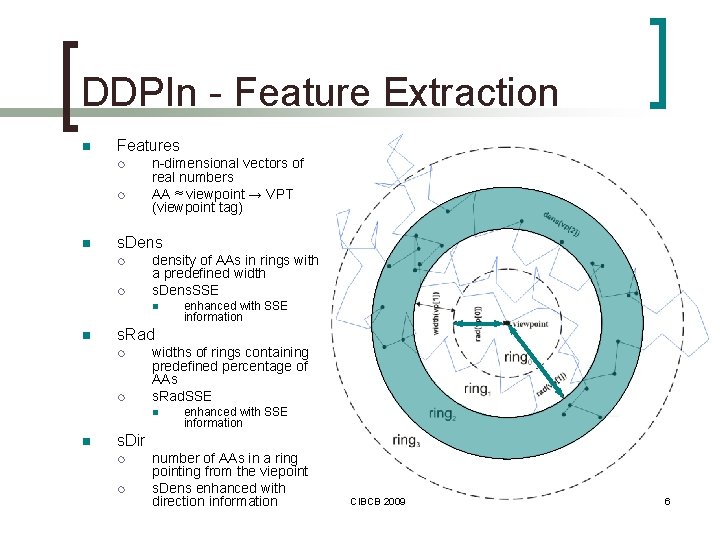
DDPIn - Feature Extraction n Features ¡ ¡ n n-dimensional vectors of real numbers AA ≈ viewpoint → VPT (viewpoint tag) s. Dens ¡ ¡ density of AAs in rings with a predefined width s. Dens. SSE n n s. Rad ¡ ¡ widths of rings containing predefined percentage of AAs s. Rad. SSE n n enhanced with SSE information s. Dir ¡ ¡ number of AAs in a ring pointing from the viepoint s. Dens enhanced with direction information CIBCB 2009 6

DDPIn - Similarity of VPTs n Metrics ¡ L 2 ¡ weighted L 2 n close neighborhood of VPs is more important CIBCB 2009 7

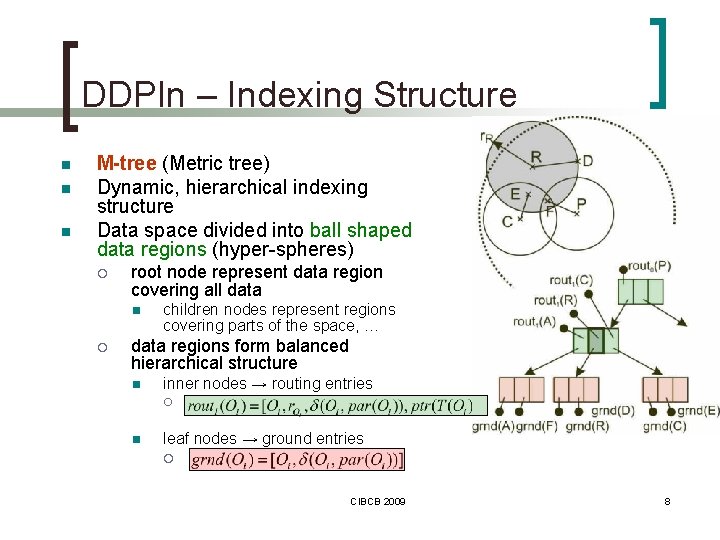
DDPIn – Indexing Structure n n n M-tree (Metric tree) Dynamic, hierarchical indexing structure Data space divided into ball shaped data regions (hyper-spheres) ¡ root node represent data region covering all data n ¡ children nodes represent regions covering parts of the space, … data regions form balanced hierarchical structure n inner nodes → routing entries ¡ n leaf nodes → ground entries ¡ CIBCB 2009 8

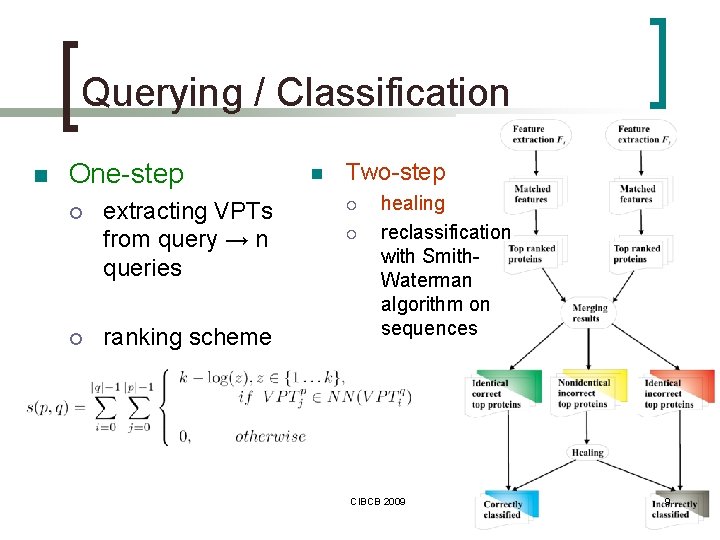
Querying / Classification n One-step ¡ ¡ extracting VPTs from query → n queries ranking scheme n Two-step ¡ ¡ healing reclassification with Smith. Waterman algorithm on sequences CIBCB 2009 9

Experimental Results n SCOP 1. 65 dataset ¡ class → fold → superfamily → family ¡ 1810 proteins n 181 superfamilies ¡ ¡ n query set ¡ ¡ ¡ n at least 10 proteins each all α, all β, α + β and α /β classes reduced - 181 queries full used also by PSI, Pro. Gre. SS, PSIST methods Testing of ¡ ¡ superfamily classification accuracy fold classification accuracy CIBCB 2009 10

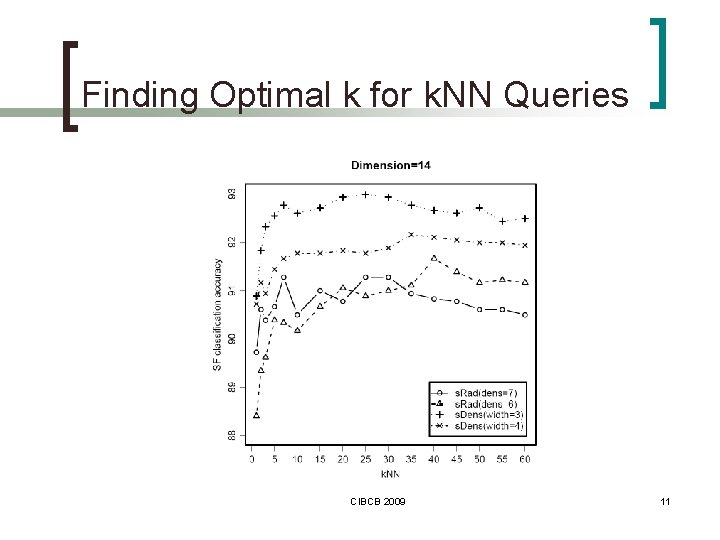
Finding Optimal k for k. NN Queries CIBCB 2009 11

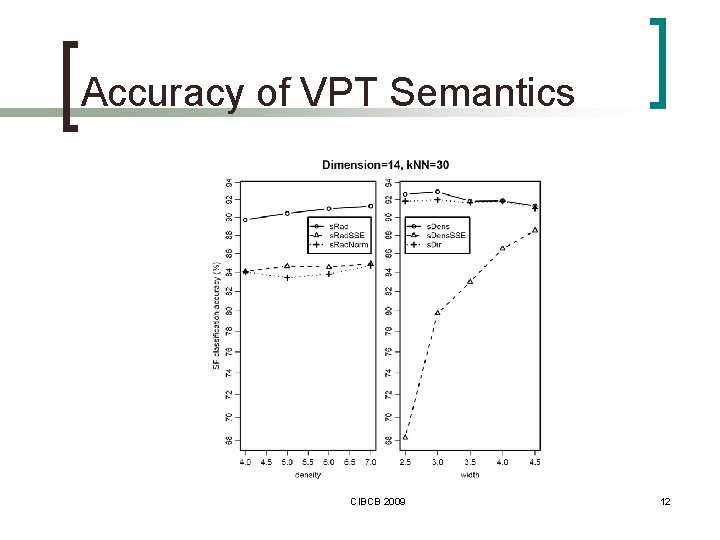
Accuracy of VPT Semantics CIBCB 2009 12

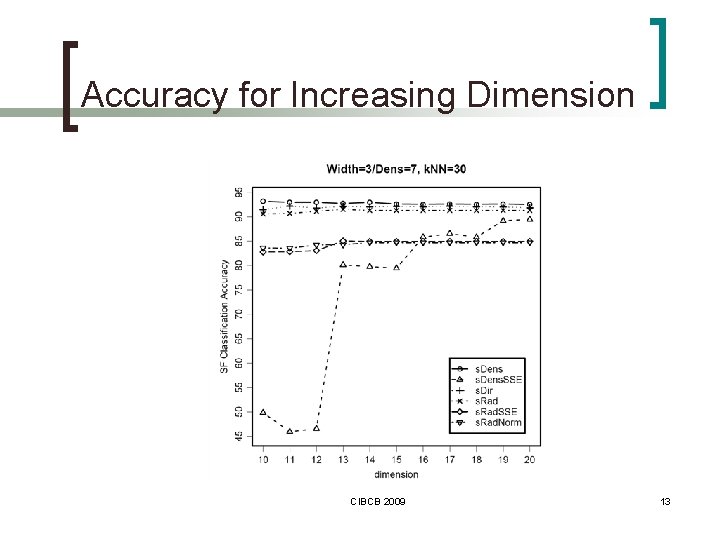
Accuracy for Increasing Dimension CIBCB 2009 13

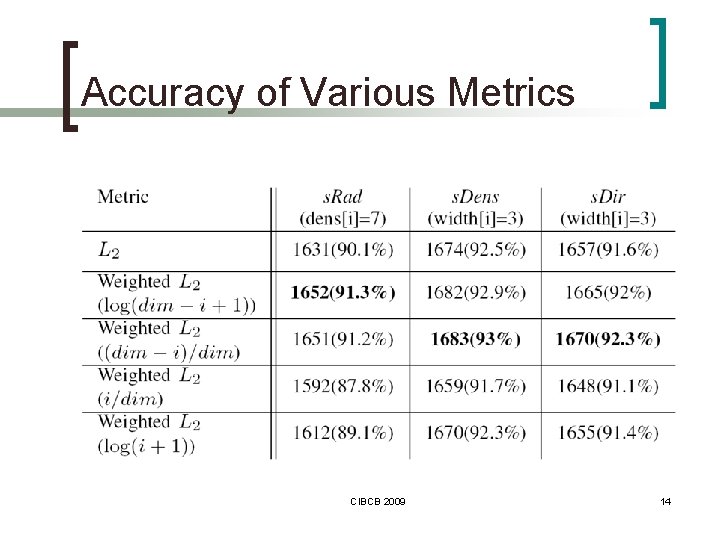
Accuracy of Various Metrics CIBCB 2009 14

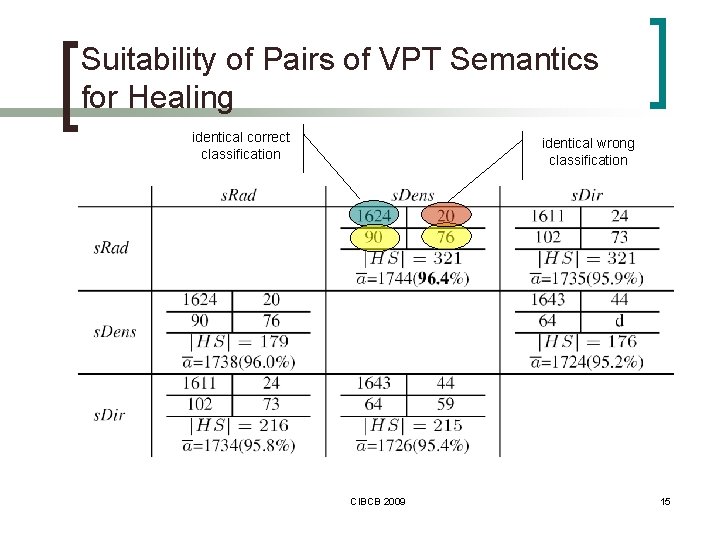
Suitability of Pairs of VPT Semantics for Healing identical correct classification identical wrong classification CIBCB 2009 15

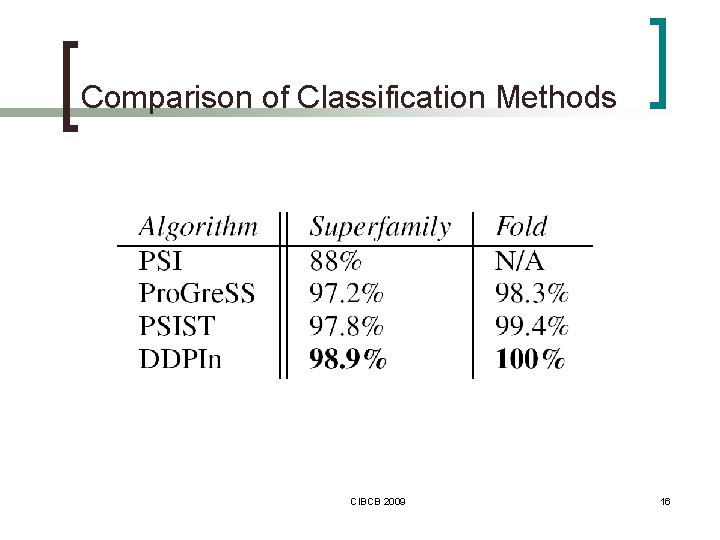
Comparison of Classification Methods CIBCB 2009 16

Conclusion n We have proposed ¡ new representation of protein structures n n We implemented ¡ ¡ n distance and density of Cα atoms ranking scheme two-step classification M-tree indexing for proposed representation classification against SCOP Experimental results ¡ best results among methods using identical classification n n ¡ 98. 9% superfamily classification accuracy 100% fold classification accuracy comparable run time CIBCB 2009 17