dd Ball Spotting Anomalies in Weighted Graphs Leman

dd. Ball: Spotting Anomalies in Weighted Graphs Leman Akoglu, Mary Mc. Glohon, Christos Faloutsos Carnegie Mellon University School of Computer Science Pittsburgh, Pennsylvania, USA

Motivation n Anomaly detection in networks (graph data) has important applications: n Computer networks spammers, port scanners n Phone-call networks telemarketers, misbehaving costumers, faulty equipment n Social networks ‘popularity contests’ n Account networks scammers, transfer fraud n Terrorist networks tight groups of people PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 2

Problem Q 1. Given a weighted and unlabeled graph, how can we spot strange, abnormal, extreme nodes? Q 2. Can we explain why the spotted nodes are anomalous? PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 3

Preliminaries I – What is an anomaly? n No clear and unique definition! “An observation that deviates so much from other observations as to arouse suspicion that it was generated by a different mechanism. ” [Hawkins, 80] PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 4

Preliminaries II – Weights $15 K $10 K 3 1 Bipartite PAKDD 2010 Unipartite Akoglu, Mc. Glohon, Faloutsos 5

Preliminaries III – Power Laws Pr[X≥x] ~ cx-α ln(Pr[X≥x]) ~ -α(c lnx) c ≥ 0, α ≥ 0 slope = -α log-log plot lin-lin plot PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 6

‘Power Law’ Example Total weight #Source nodes #Destination nodes # Edges DBLP Keyword-to-Conference Network Densification Power Law [Leskovec ‘ 05] Weight Power Law [Mc. Glohon ‘ 08] PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 7

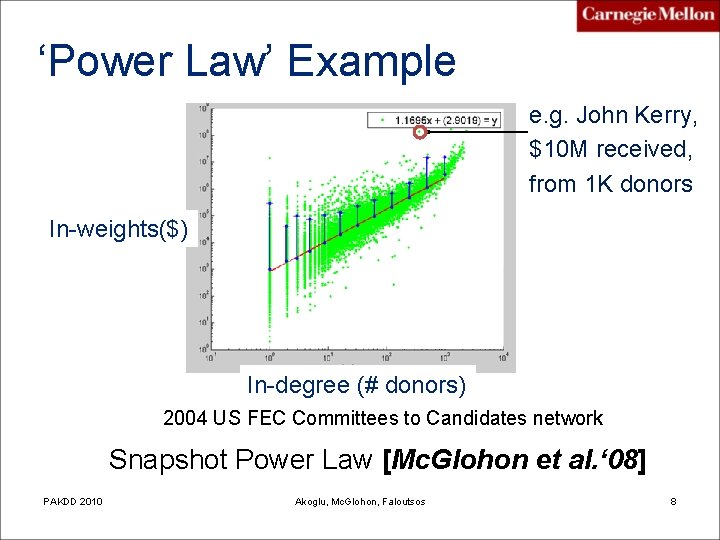
‘Power Law’ Example e. g. John Kerry, $10 M received, from 1 K donors In-weights($) In-degree (# donors) 2004 US FEC Committees to Candidates network Snapshot Power Law [Mc. Glohon et al. ‘ 08] PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 8

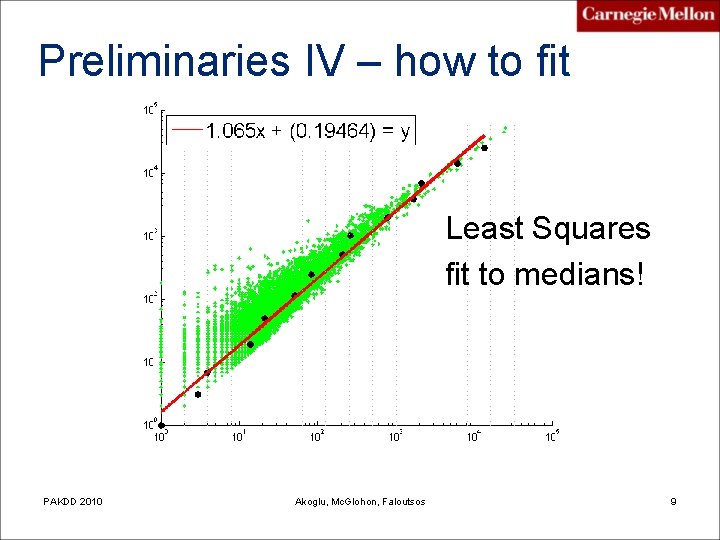
Preliminaries IV – how to fit Least Squares fit to medians! PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 9

Problem revisited Q 1. Given a weighted and unlabeled graph, how can we spot strange, abnormal, extreme nodes? Q 2. Can we explain why the spotted nodes are anomalous? PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 10

Problem sketch PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 11

Main idea For each node, P. 1) extract ‘ego-net’ (=1 -step-away neighbors) P. 2) extract features (#edges, total weight, etc. ) P. 3) extract patterns (norms) P. 4) anomaly detection: compare with the rest of the population LLNL'10 C. Faloutsos (CMU) 12

Outline 1. Motivation 2. Preliminaries and Problem Definition 3. Proposed Method a. Study of ego-nets b. Laws and Observations c. Anomaly detection 1. Datasets 2. Experiments 3. Discussion & Conclusion PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 13

P. 1 What is an egonet? ego-net ego PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 14

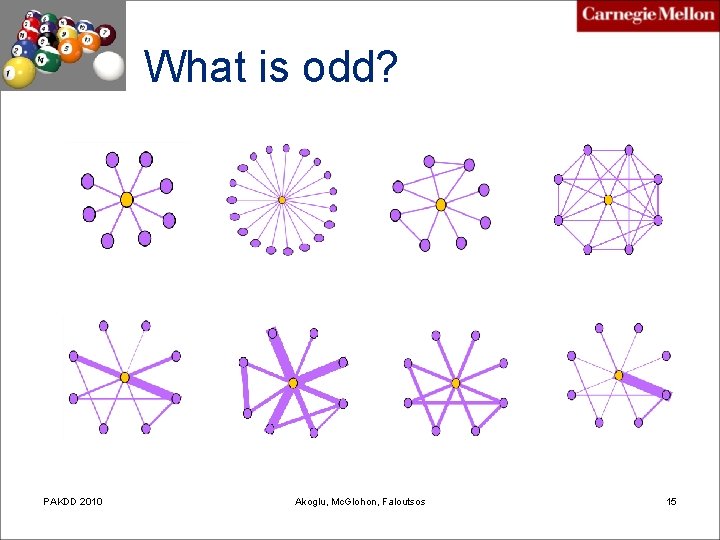
What is odd? PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 15

What is “anomalous”? telemarketer, port scanner, people adding friends indiscriminatively, etc. Near-star tightly connected people, terrorist groups? , discussion group, etc. Pw. C 2009 Leman Akoglu Near-clique 16

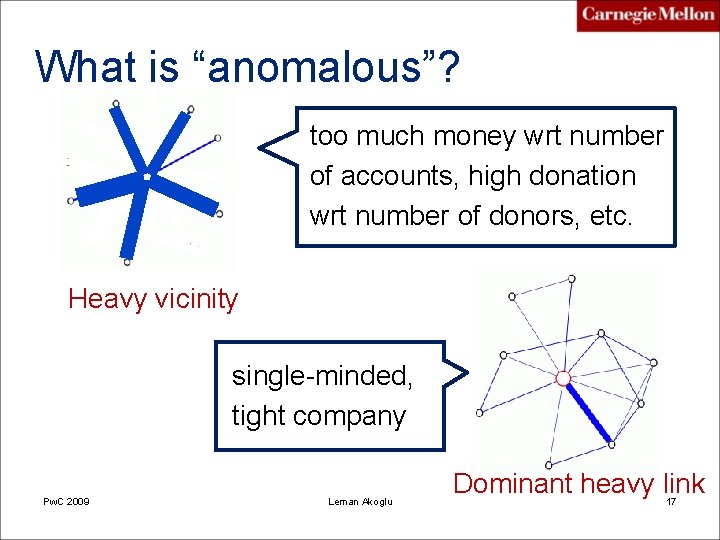
What is “anomalous”? too much money wrt number of accounts, high donation wrt number of donors, etc. Heavy vicinity single-minded, tight company Pw. C 2009 Leman Akoglu Dominant heavy link 17

P. 2 What features… … should we extract so that to project nodes into a lowdimensional space? features that could yield “laws” features easy to compute and interpret Pw. C 2009 Leman Akoglu 18

Selected Features § § Ni: number of neighbors (degree) of ego i Ei: number of edges in egonet i Wi: total weight of egonet i λw, i: principal eigenvalue of the weighted adjacency matrix of egonet i PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 19

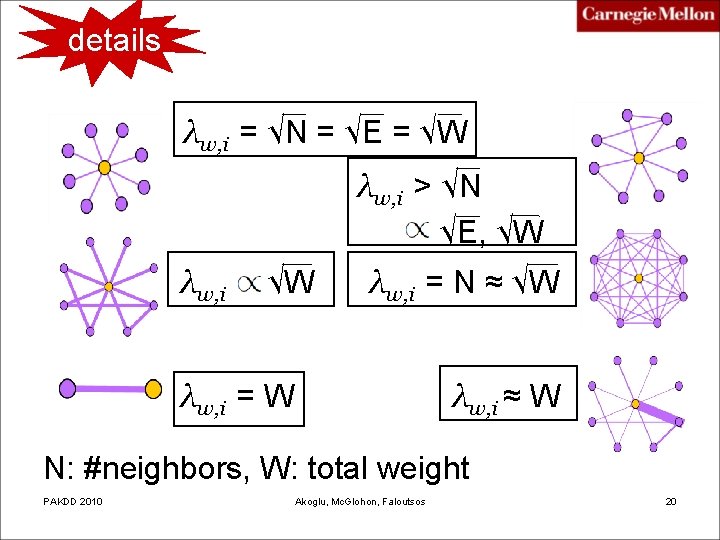
details λw, i = √N = √E = √W λw, i > √N ~ √E, √W λw, i = N ≈ √W λw, i = W λw, i ≈ W N: #neighbors, W: total weight PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 20

Other Features § § § Si: number of singleton neighbors of ego i with degree 1 max(Wi): maximum edge weight in egonet i max(Wi, d=1): maximum edge weight to/from a degree 1 neighbor of ego i max(di): maximum degree of the neighbors of ego i 2 -step neighborhood features PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 21

Outline 1. Motivation 2. Preliminaries 3. Proposed Method a. Study of egonets b. Laws and Observations c. Anomaly detection 4. Datasets 5. Experiments 6. Discussion & Conclusion PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 22

P. 3 What patterns? Observation 1: Egonet Density Power Law (EDPL) Q 1: How does the number of neighbors N of the egonet relate to the number of edges E? PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 23

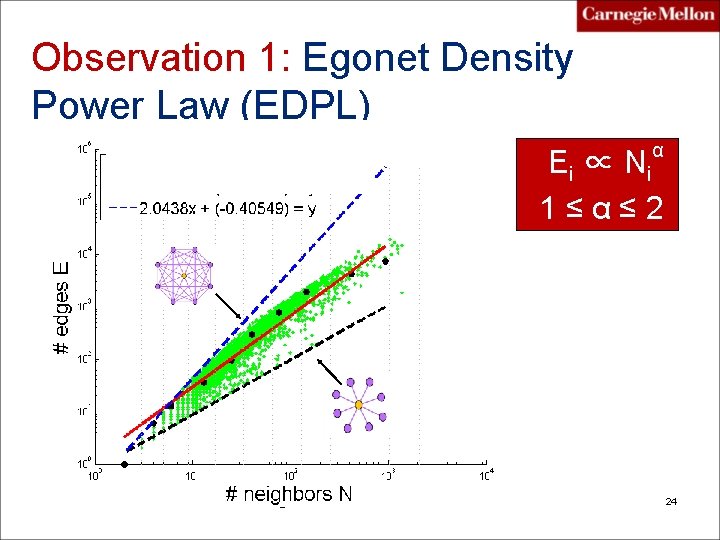
Observation 1: Egonet Density Power Law (EDPL) α E i ∝ Ni 1≤α≤ 2 Pw. C 2009 Leman Akoglu 24

P. 3 What patterns? Observation 2: Egonet Weight Power Law (EWPL) Q 2: How does the total weight W of the egonet relate to the number of edges E? PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 25

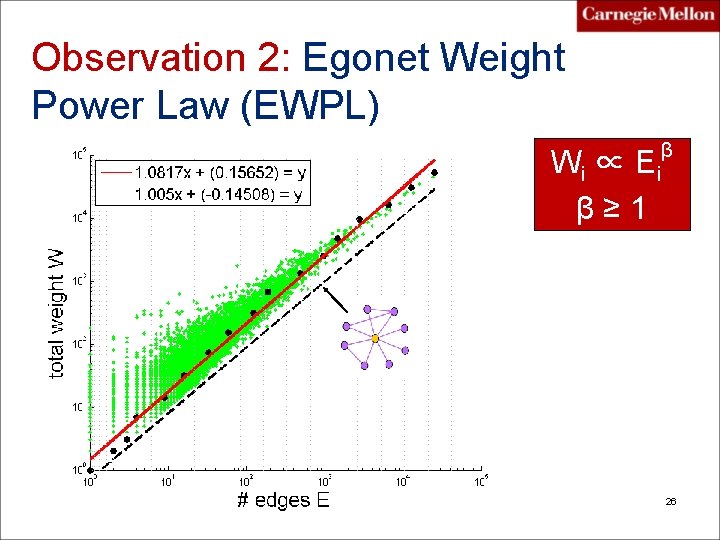
Observation 2: Egonet Weight Power Law (EWPL) Wi ∝ E i β≥ 1 β 26

P. 3 What patterns? Observation 3: Egonet λw Power Law (ELWPL) Q 3: How does the largest eigenvalue λw of the weighted adjacency matrix of the egonet relate to the total weight W? PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 27

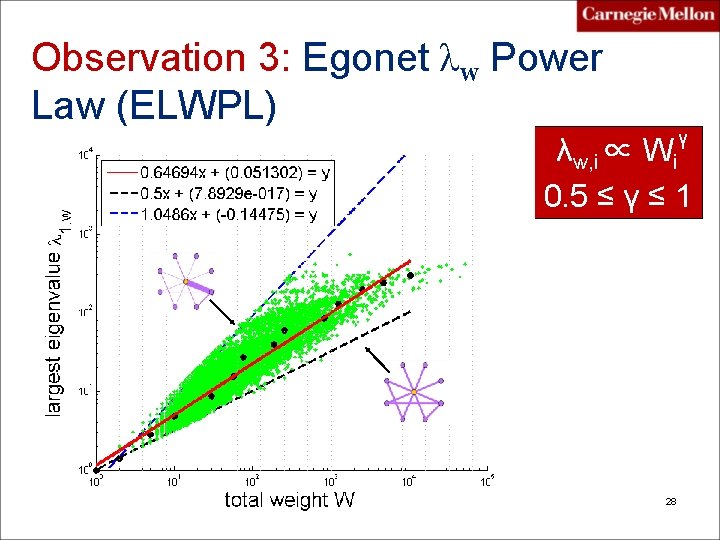
Observation 3: Egonet λw Power Law (ELWPL) γ λw, i ∝ Wi 0. 5 ≤ γ ≤ 1 28

Outline 1. Motivation 2. Preliminaries 3. Proposed Method a. Study of egonets b. Laws and Observations c. Anomaly detection 4. Datasets 5. Experiments 6. Discussion & Conclusion PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 29

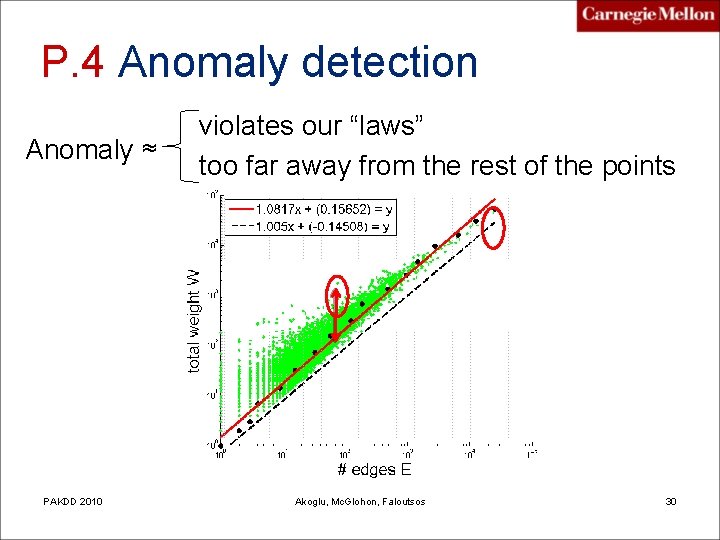
P. 4 Anomaly detection Anomaly ≈ PAKDD 2010 violates our “laws” too far away from the rest of the points Akoglu, Mc. Glohon, Faloutsos 30

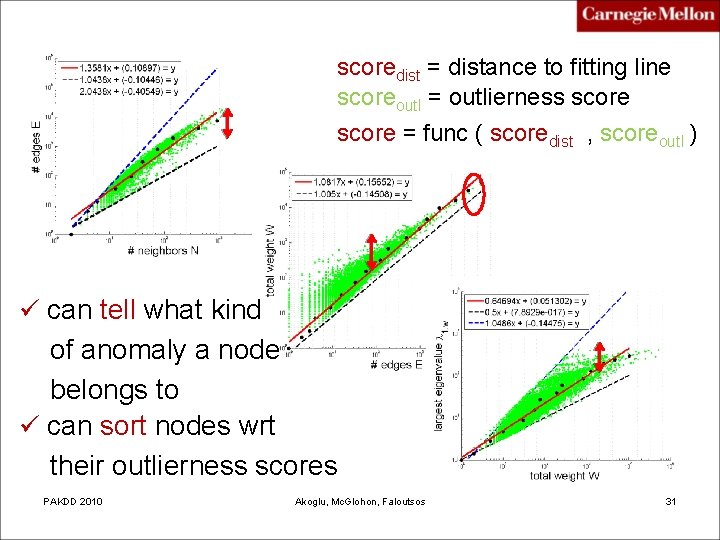
scoredist = distance to fitting line scoreoutl = outlierness score = func ( scoredist , scoreoutl ) ü can tell what kind of anomaly a node belongs to ü can sort nodes wrt their outlierness scores PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 31

Outline 1. Motivation 2. Preliminaries 3. Proposed Method a. Study of egonets b. Laws and Observations c. Anomaly detection 4. Datasets 5. Experiments 6. Discussion & Conclusion PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 32

Datasets Bipartite networks: 1. Don 2 Com 2 Cand 3. Auth 2 Conf |N| 1. 6 M 6 K 421 K |E| 2 M 125 K 1 M Unipartite networks: 5. Blog. Net 6. Post. Net 7. Enron 8. Oregon 38 K PAKDD 2010 |N| 27 K 223 K 36 K 11 K |E| 126 K 217 K 183 K Akoglu, Mc. Glohon, Faloutsos 33

Outline 1. Motivation 2. Preliminaries 3. Proposed Method a. Study of egonets b. Laws and Observations c. Anomaly detection 4. Datasets 5. Experiments 6. Discussion & Conclusion PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 34

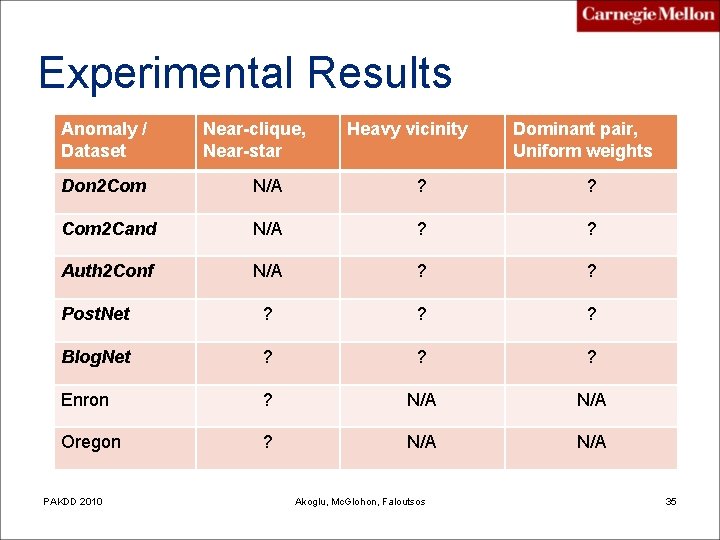
Experimental Results Anomaly / Dataset Near-clique, Near-star Heavy vicinity Dominant pair, Uniform weights Don 2 Com N/A ? ? Com 2 Cand N/A ? ? Auth 2 Conf N/A ? ? Post. Net ? ? ? Blog. Net ? ? ? Enron ? N/A Oregon ? N/A PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 35

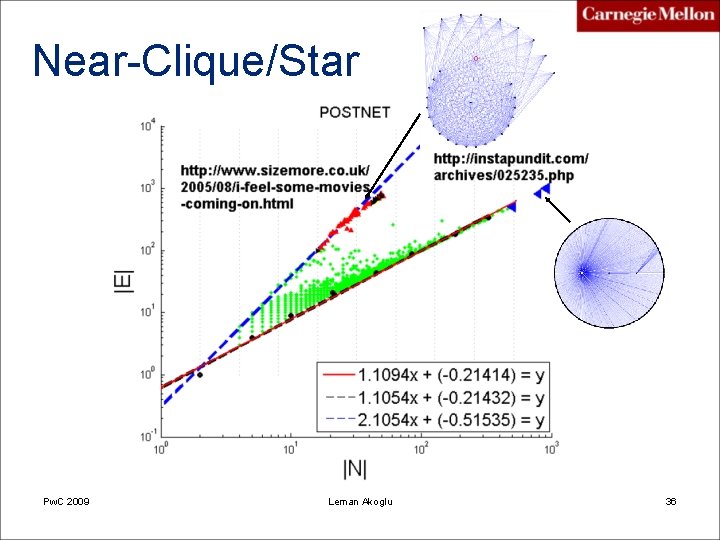
Near-Clique/Star Pw. C 2009 Leman Akoglu 36

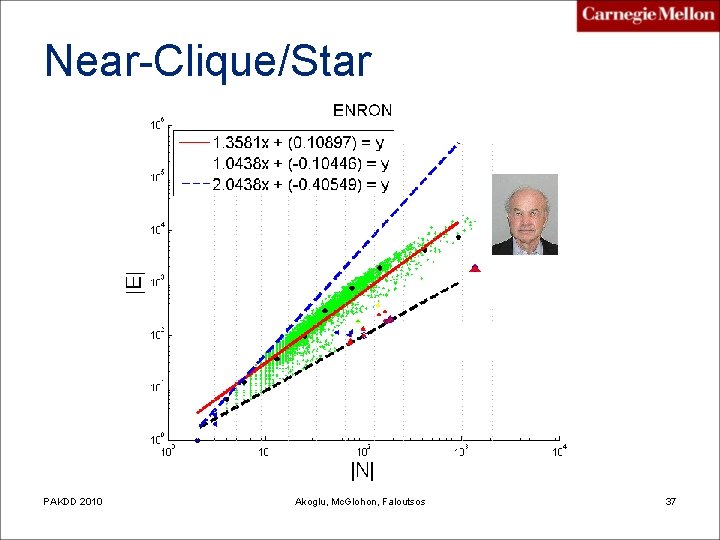
Near-Clique/Star PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 37

Experimental Results Anomaly / Dataset Near-clique, Near-star Heavy vicinity Dominant pair, Uniform weights Don 2 Com N/A ? ? Com 2 Cand N/A ? ? Auth 2 Conf N/A ? ? Post. Net self-linking post, post w/ numerous links to diverse posts ? ? Blog. Net “link blogs” devoted to a wide array of content ? ? Kenneth Lay (>1 K contacts) N/A 3 large ASPs, Verizon, Sprint, AT&T N/A Enron Oregon PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 38

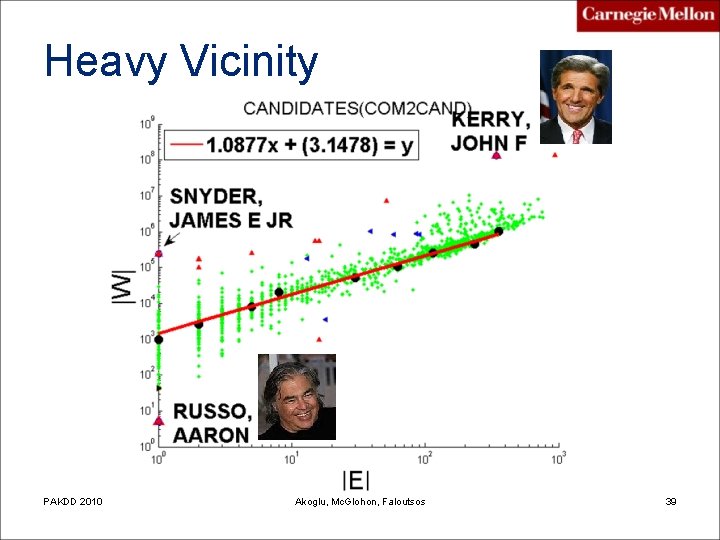
Heavy Vicinity PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 39

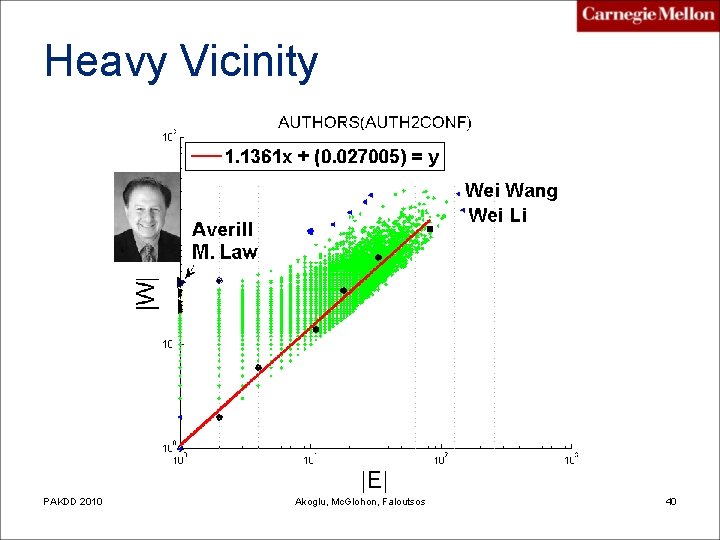
Heavy Vicinity PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 40

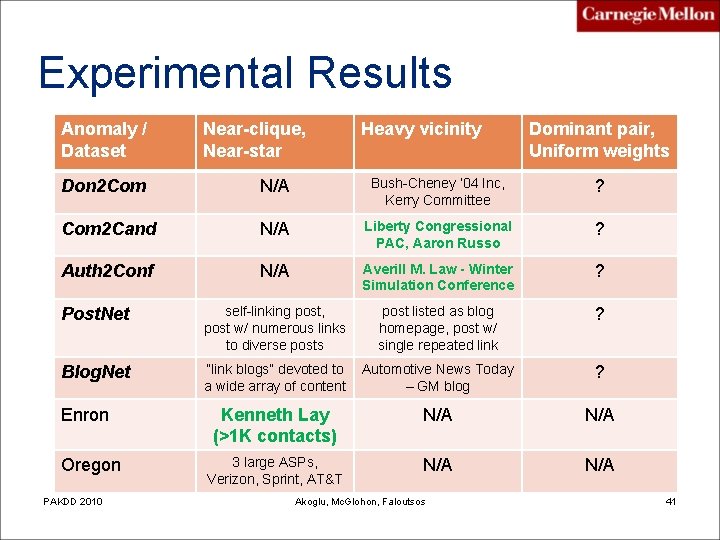
Experimental Results Anomaly / Dataset Near-clique, Near-star Heavy vicinity Dominant pair, Uniform weights Don 2 Com N/A Bush-Cheney ’ 04 Inc, Kerry Committee ? Com 2 Cand N/A Liberty Congressional PAC, Aaron Russo ? Auth 2 Conf N/A Averill M. Law - Winter Simulation Conference ? Post. Net self-linking post, post w/ numerous links to diverse posts post listed as blog homepage, post w/ single repeated link ? Blog. Net “link blogs” devoted to a wide array of content Automotive News Today – GM blog ? Kenneth Lay (>1 K contacts) N/A 3 large ASPs, Verizon, Sprint, AT&T N/A Enron Oregon PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 41

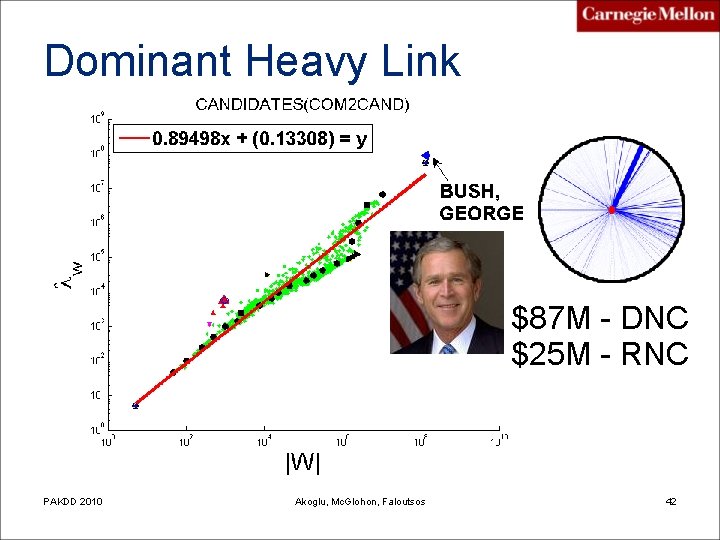
Dominant Heavy Link $87 M - DNC $25 M - RNC PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 42

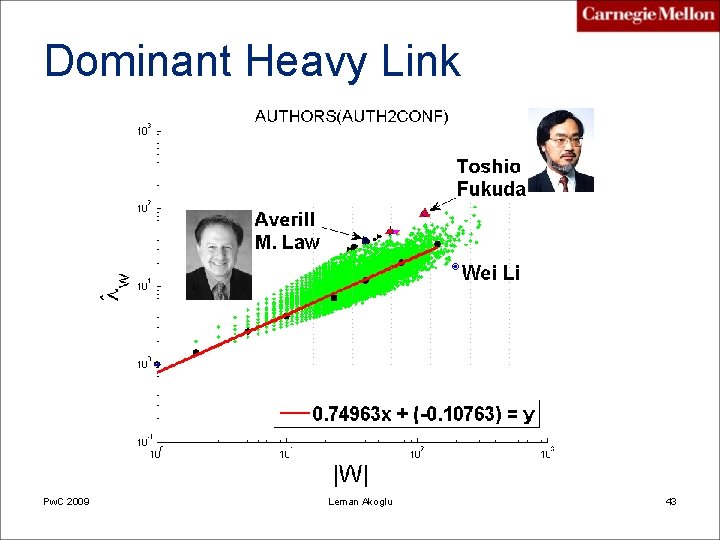
Dominant Heavy Link Pw. C 2009 Leman Akoglu 43

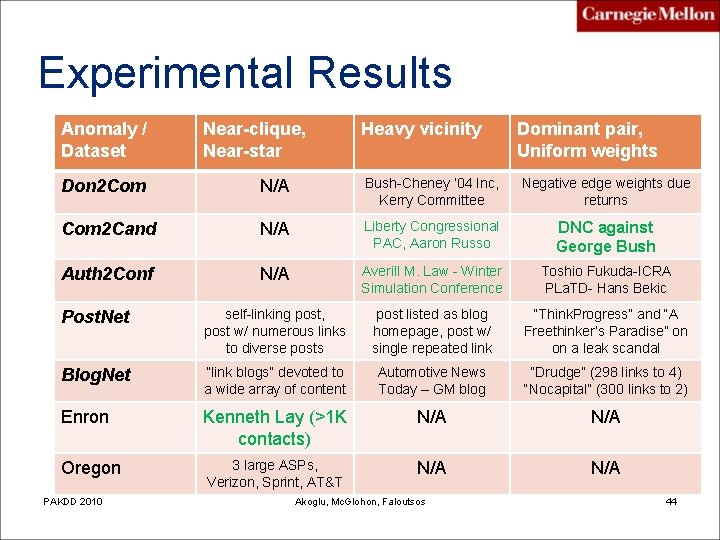
Experimental Results Anomaly / Dataset Near-clique, Near-star Heavy vicinity Dominant pair, Uniform weights Don 2 Com N/A Bush-Cheney ’ 04 Inc, Kerry Committee Negative edge weights due returns Com 2 Cand N/A Liberty Congressional PAC, Aaron Russo DNC against George Bush Auth 2 Conf N/A Averill M. Law - Winter Simulation Conference Toshio Fukuda-ICRA PLa. TD- Hans Bekic Post. Net self-linking post, post w/ numerous links to diverse posts post listed as blog homepage, post w/ single repeated link “Think. Progress” and “A Freethinker’s Paradise” on on a leak scandal Blog. Net “link blogs” devoted to a wide array of content Automotive News Today – GM blog “Drudge” (298 links to 4) “Nocapital” (300 links to 2) Enron Kenneth Lay (>1 K contacts) N/A 3 large ASPs, Verizon, Sprint, AT&T N/A Oregon PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 44

Outline 1. Motivation 2. Preliminaries 3. Proposed Method a. Study of egonets b. Laws and Observations c. Anomaly detection 4. Datasets 5. Experiments 6. Discussion & Conclusion PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 45

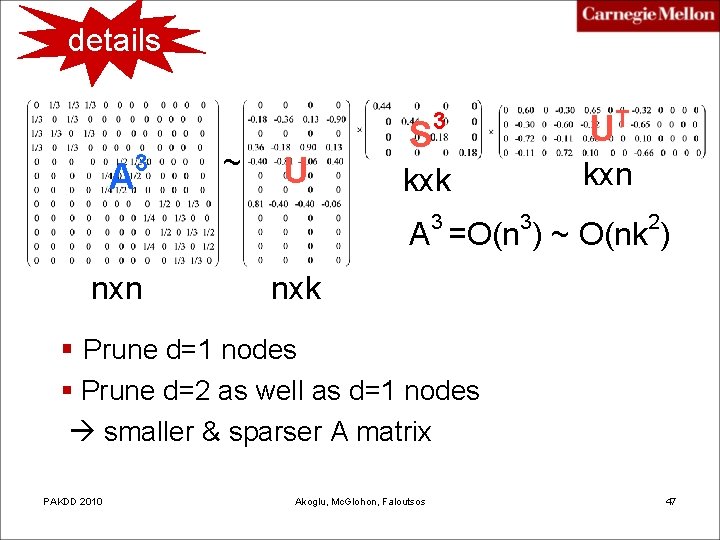
Scalability § Counting number of edges in egonets for ALL nodes is expensive! need to scan connections for all pairs of neighbors! § Can be reworded as counting local triangles § A fast method [Tsourakakis, 08] exists! IDEA: o #triangles = (# paths of length 3) / 2 3 o # paths of length 3 for node i = (A )ii 3 o Computing A is still expensive! o Low-rank approximation! PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 46

details A 3 ~ U S 3 U kxn kxk 3 T 3 2 A =O(n ) ~ O(nk ) nxn nxk § Prune d=1 nodes § Prune d=2 as well as d=1 nodes smaller & sparser A matrix PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 47

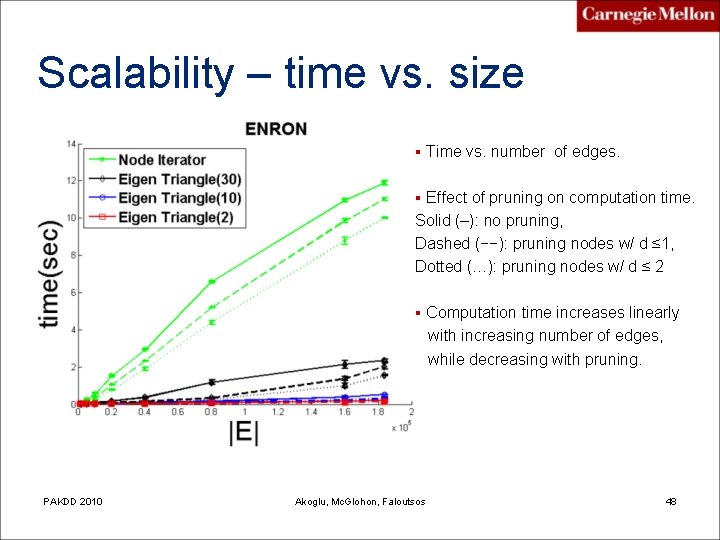
Scalability – time vs. size § Time vs. number of edges. § Effect of pruning on computation time. Solid (–): no pruning, Dashed (−−): pruning nodes w/ d ≤ 1, Dotted (…): pruning nodes w/ d ≤ 2 § Computation time increases linearly with increasing number of edges, while decreasing with pruning. PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 48

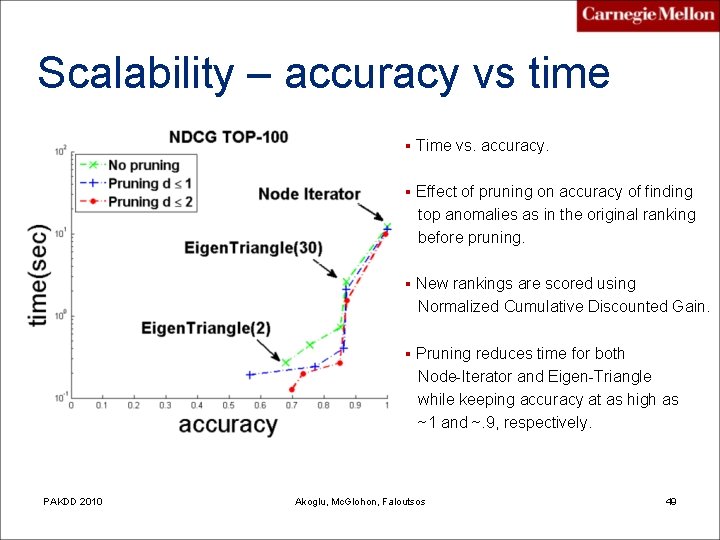
Scalability – accuracy vs time § Time vs. accuracy. § Effect of pruning on accuracy of finding top anomalies as in the original ranking before pruning. § New rankings are scored using Normalized Cumulative Discounted Gain. § Pruning reduces time for both Node-Iterator and Eigen-Triangle while keeping accuracy at as high as ~1 and ~. 9, respectively. PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 49

Conclusion n Odd. Ball, a fast, unsupervised method to detect abnormal n n nodes in weighted graphs. Study of egonets; list of numerical features Discovery of new patterns in density (Obs. 1: EDPL), weights (Obs. 2: EWPL), and principal eigenvalues (Obs. 3: ELWPL). Speed-up in feature extraction, with accuracy ~. 9 Experiments on real graphs of over 1 M nodes, that reveal strange/extreme nodes from many different domains Software available online! http: //www. cs. cmu. edu/~lakoglu/#tools PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 50

Related Work n n n Noble and Cook [KDD, 03] detect anomalous sub-graphs using variants of the MDL principle. Eberle and Holder [ICDM, 07] detect unexpected/missing nodes/edges in labeled graphs. Liu et. al [SDM, 05] detect non-crashing bugs in software using frequent execution flow graphs combined with supervised classification. Sun et al. [ICDM, 05] use proximity and random walks to assess normality of nodes in bipartite graphs. Chakrabarti [PKDD, 04] spot anomalous edges as a byproduct of cross-associations. PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 51

QUESTIONS? http: //www. cs. cmu. edu/~lakoglu/#tools 52

Odd. Ball over time? n Rank nodes at each time tick t n Node i will have rank vector Ri ri, 1 ri, 2 … ri, t n Sort nodes w. r. t. |Ri<=threshold| n threshold =3 will sort nodes w. r. t. the number of time- ticks they appear in top 3 outliers n Note: not all nodes appear at all time-ticks PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 53

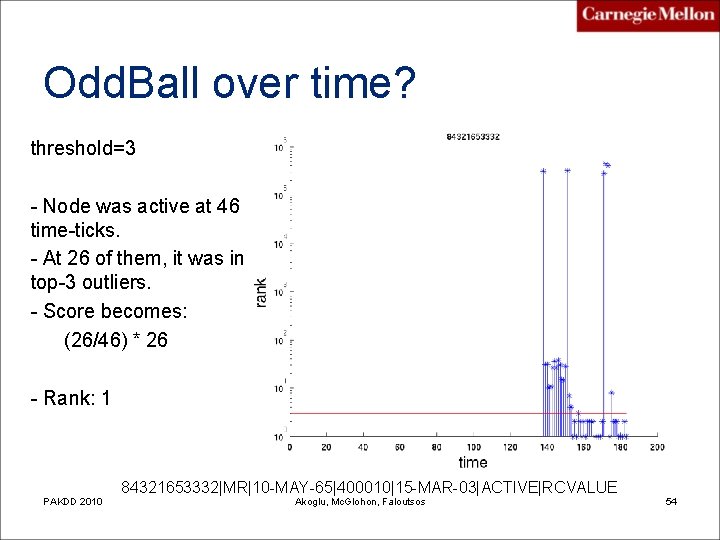
Odd. Ball over time? threshold=3 - Node was active at 46 time-ticks. - At 26 of them, it was in top-3 outliers. - Score becomes: (26/46) * 26 - Rank: 1 PAKDD 2010 84321653332|MR|10 -MAY-65|400010|15 -MAR-03|ACTIVE|RCVALUE Akoglu, Mc. Glohon, Faloutsos 54

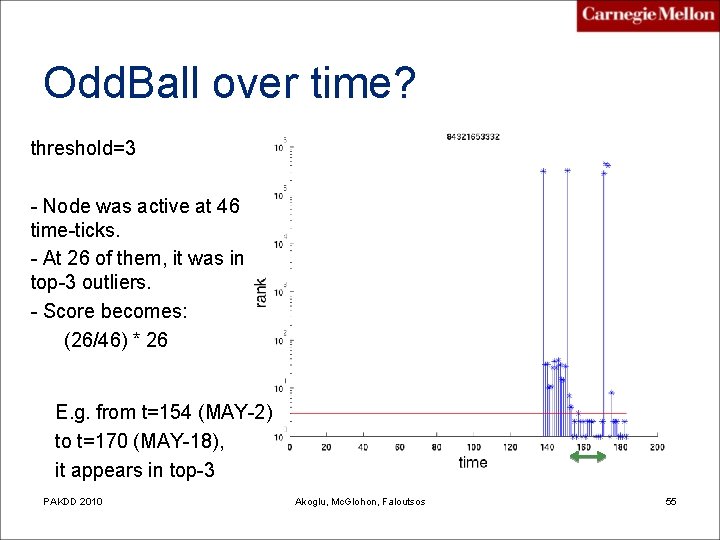
Odd. Ball over time? threshold=3 - Node was active at 46 time-ticks. - At 26 of them, it was in top-3 outliers. - Score becomes: (26/46) * 26 E. g. from t=154 (MAY-2) to t=170 (MAY-18), it appears in top-3 PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 55

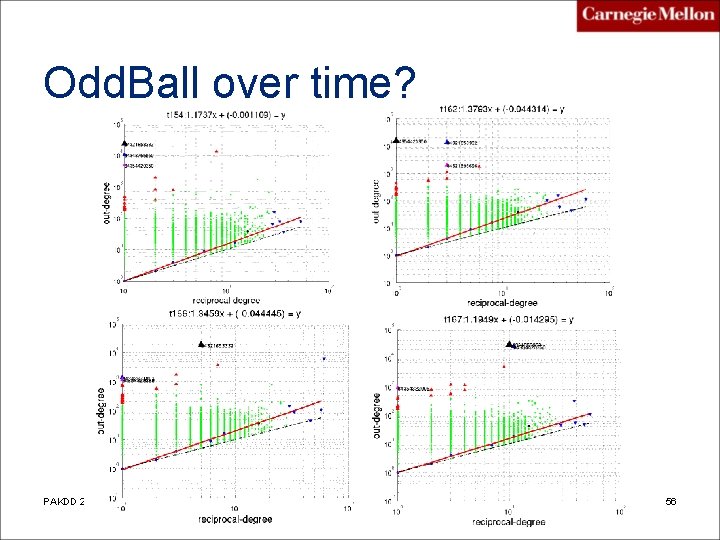
Odd. Ball over time? PAKDD 2010 Akoglu, Mc. Glohon, Faloutsos 56

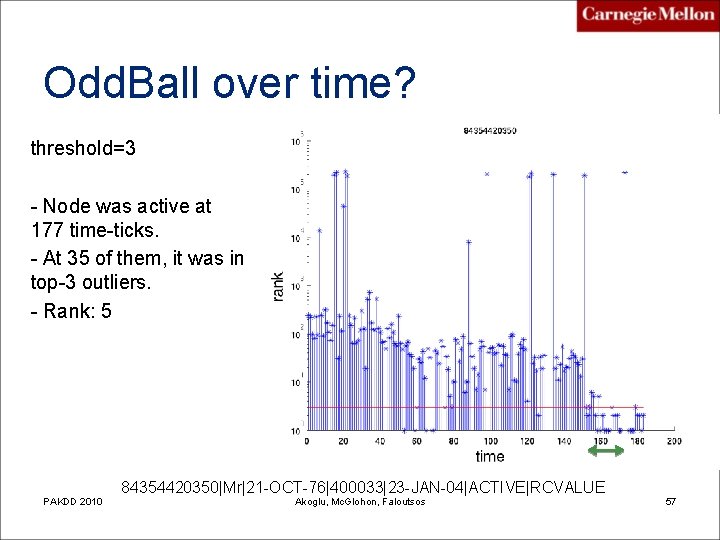
Odd. Ball over time? threshold=3 - Node was active at 177 time-ticks. - At 35 of them, it was in top-3 outliers. - Rank: 5 PAKDD 2010 84354420350|Mr|21 -OCT-76|400033|23 -JAN-04|ACTIVE|RCVALUE Akoglu, Mc. Glohon, Faloutsos 57

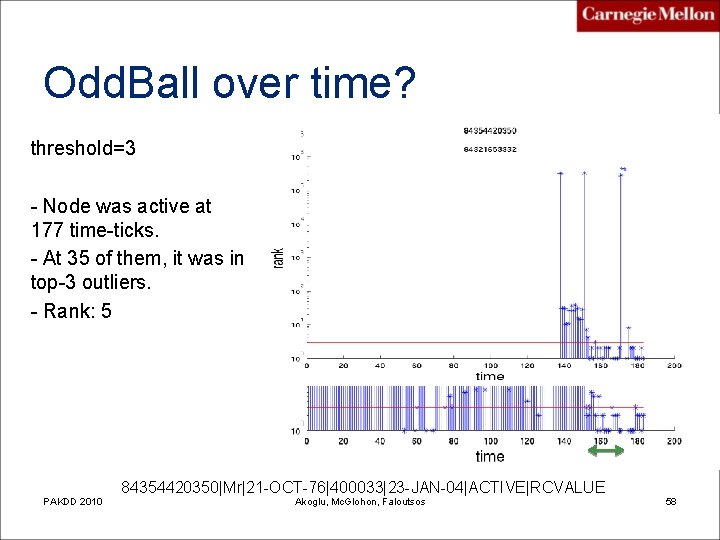
Odd. Ball over time? threshold=3 - Node was active at 177 time-ticks. - At 35 of them, it was in top-3 outliers. - Rank: 5 PAKDD 2010 84354420350|Mr|21 -OCT-76|400033|23 -JAN-04|ACTIVE|RCVALUE Akoglu, Mc. Glohon, Faloutsos 58